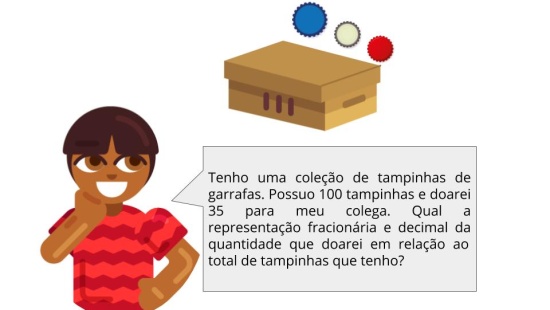
Resumo da aula
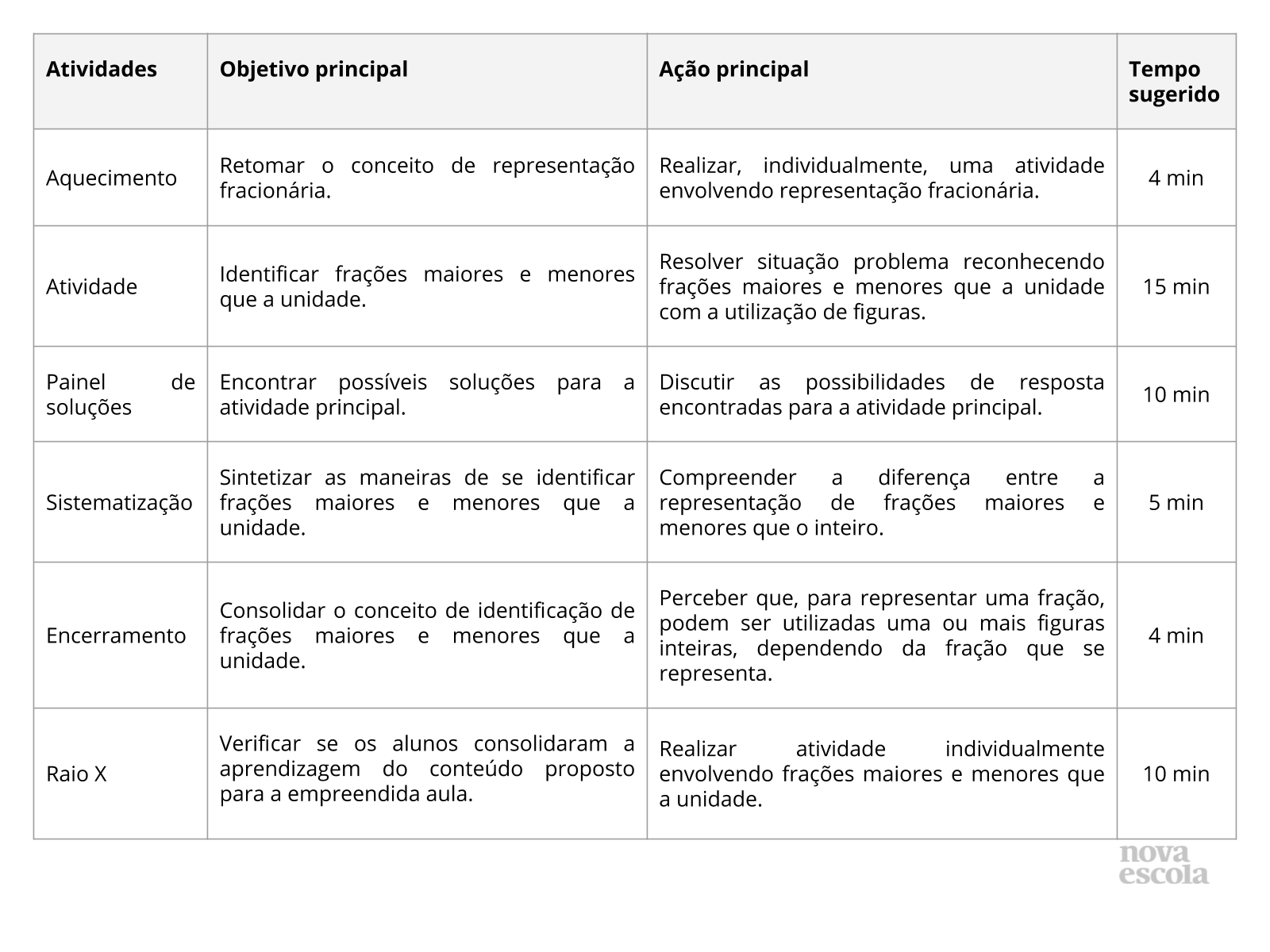
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

- Tempo sugerido: 2 minutos
- Orientação: Apenas leia o objetivo para a turma, ressaltando a importância da colaboração dos alunos para atingir as metas estabelecidas para a aula.
Aquecimento
Tempo sugerido: 4 minutos
Orientação: Inicie a atividade lembrando ao aluno que toda fração é composta por um numerador e por um denominador, sendo que o numerador indica o total de partes que a figura contém e o denominador indica o total de partes pintadas. Portanto, estes termos variam de acordo com cada figura representada.
Propósito: Retomar o conceito de representação fracionária a partir de figuras geométricas.
Discuta com a turma:
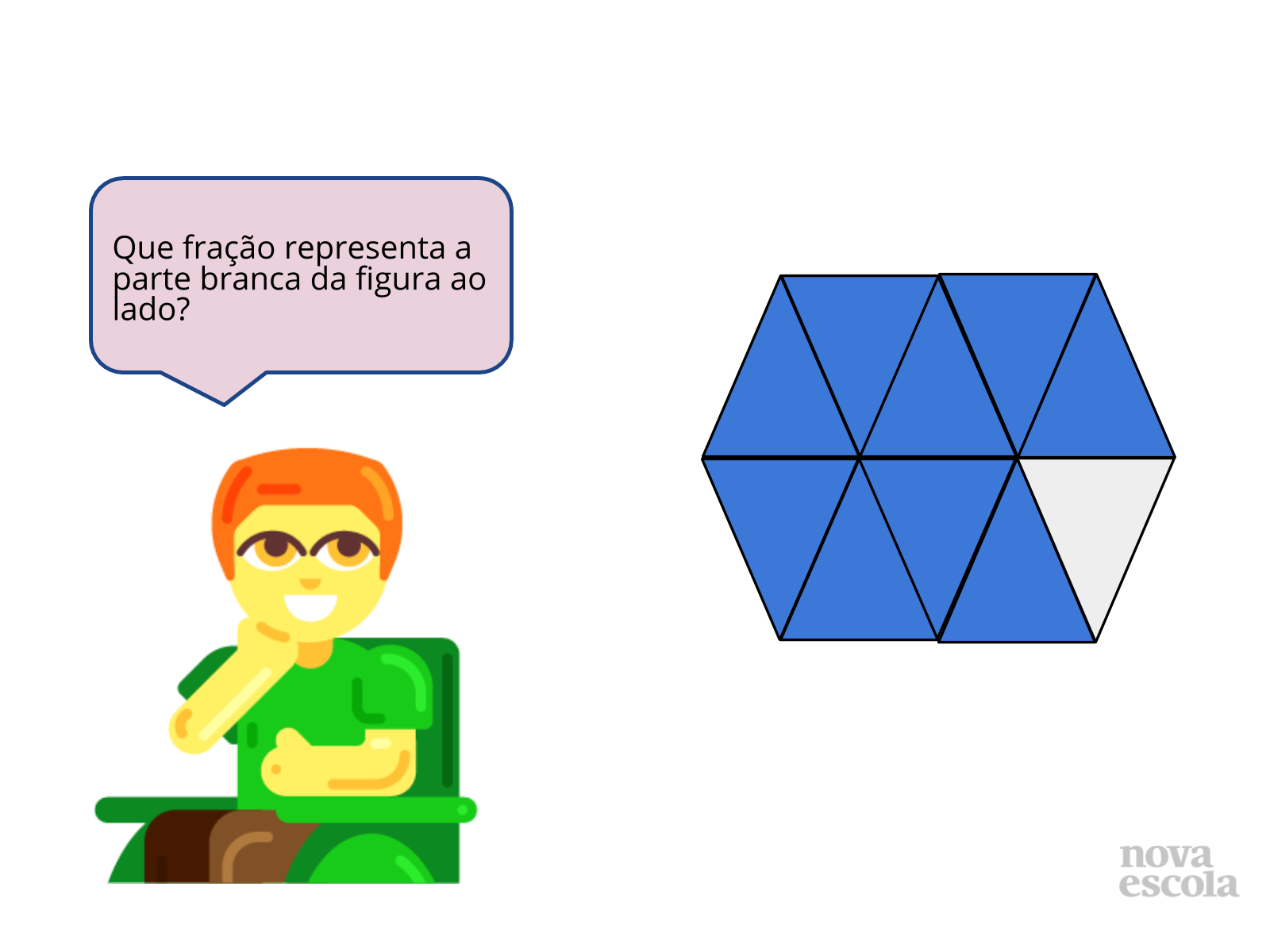
- Quantas partes tem a figura apresentada?
- Quantas partes estão azuis? E brancas?
- Qual deverá ser o denominador da fração? Por quê?
- Para representar a parte branca da figura, qual será o numerador? E se quiséssemos representar a parte azul?
- Então, que fração representa a parte branca?
Atividade principal 1

Tempo sugerido: 15 minutos (Slides 4 e 5).
Orientação: Nesta atividade estamos trabalhando com grandezas discretas, que envolvem objetos do dia a dia dos alunos. Por isso, é importante serem trabalhadas, uma vez que diariamente os alunos terão contato com frações de quantidades como a apresentada na questão. Antes de iniciar a atividade, lembre aos alunos que a quantidade total de partes (ovos) da cartela representa a unidade (ou o todo) e, portanto, corresponde ao denominador. O numerador, por sua vez, será a quantidade de partes (ovos) utilizadas. Assim, a fração indica a relação entre o número de partes representado e o total de partes. Portanto, podem existir várias frações para uma mesma imagem, ou seja, frações equivalentes.
Propósito: Identificar frações menores que a unidade.
Discuta com a turma:
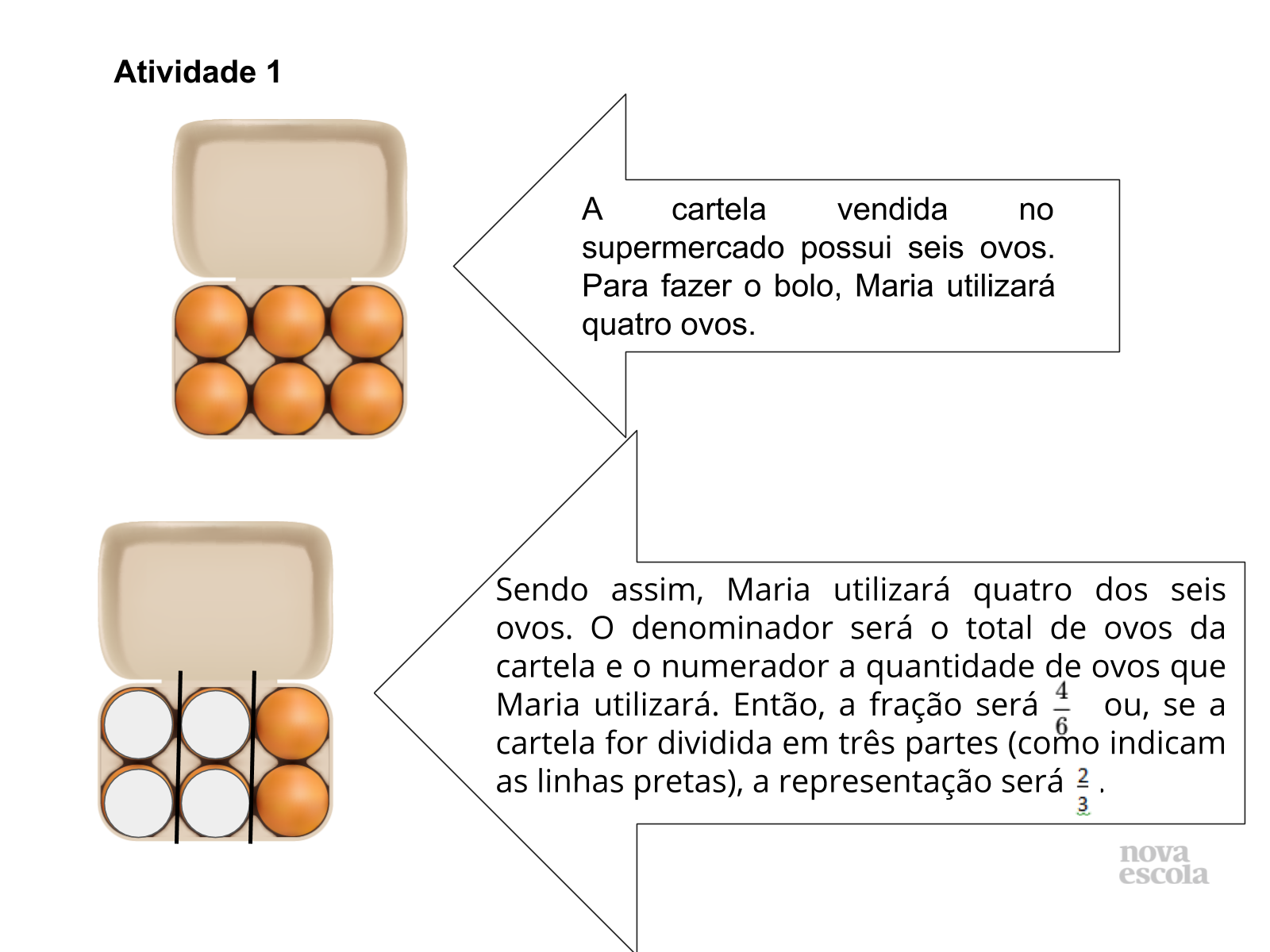
- Quantos ovos possui a cartela?
- Quantos ovos Maria utilizará para fazer o bolo?
- A quantidade que Maria utilizará é maior ou menor que a quantidade de ovos da cartela?
Materiais Complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal 2

Tempo sugerido: 15 minutos (Slides 4 e 5).
Orientação: Retomar com os alunos o conceito de numerador e denominador, enfatizando o fato de que o denominador deve corresponder ao total de partes em que cada unidade foi dividida. Neste caso, corresponde ao total de partes (ovos) em que cada cartela é dividida. O que sofre alterações a depender da quantidade de ovos utilizados é o numerador. Para realizar esta atividade, o aluno deve perceber que a fração é uma parte da unidade, e compreender que essa unidade pode ser um objeto qualquer, uma coleção (como um álbum de figurinhas, de fotos, carrinhos, entre outros)
Propósito: Reconhecer frações maiores que a unidade.
Discuta com a turma:
- Quantos ovos há em cada cartela?
- Quantos ovos Maria utilizará nesta receita?
- Qual será o numerador e denominador da fração?
- Maria utilizará mais ou menos de uma cartela inteira para fazer o bolo?
- Quantos ovos utilizará de cada cartela?
- A fração que representa o total de ovos que Maria utilizará é maior ou menor que a unidade?
Materiais Complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão da solução
Tempo sugerido: 10 minutos (Slides 6 e 7).
Orientação: Deixe que os alunos identifiquem o numerador e o denominador da fração, lembrando aos mesmos que o denominador indica sempre o total de partes que compõe a unidade. Alguns alunos verão a cartela de ovos como três grupos com dois ovos cada um e, assim, indicar a fração ? para representar a quantidade de ovos que Maria utilizará, outros verão a cartela com seis ovos e representarão a fração 4/6, que é equivalente a ?. Professor, é uma ótima oportunidade para fazer uma revisão sobre equivalência de frações e assim proporcionar a construção do conceito para os alunos que apresentam dificuldade de reconhecer a equivalência de frações nessa situação.
Propósito: Identificar frações menores que a unidade.
Discuta com a turma:
- Qual será o denominador da fração? E o numerador?
- Quantos ovos sobraram?
- Que fração representa os ovos que sobraram?
- Maria utilizará mais ou menos de uma cartela de ovos?
- A fração correspondente aos ovos que Maria utilizará é maior ou menor que a unidade? Por quê?
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão da solução
Tempo sugerido: 10 minutos (Slides 6 e 7).
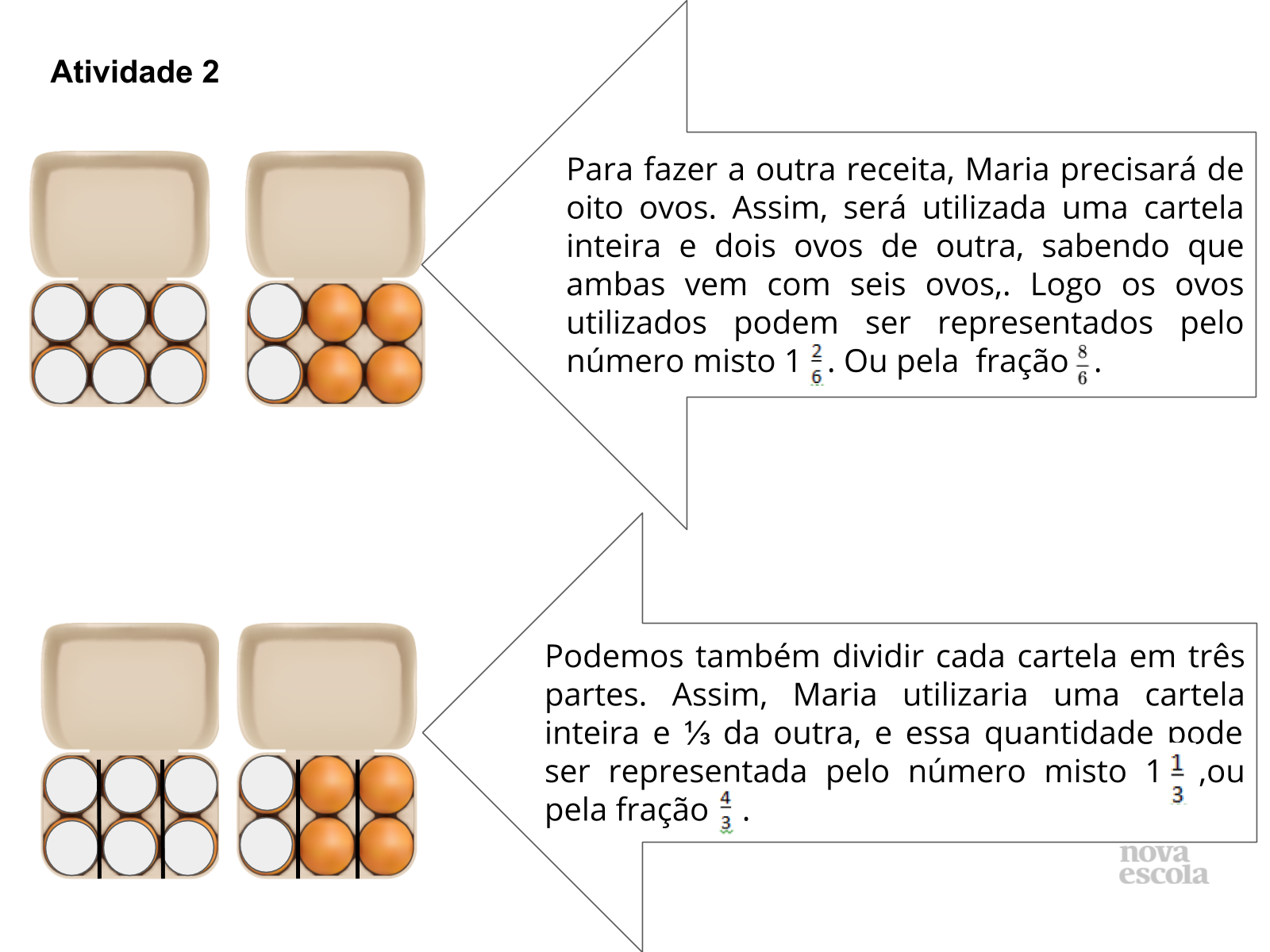
Orientação: Incentive os alunos a perceberem que apenas uma cartela de ovos não será suficiente para que Maria faça sua receita, pois uma cartela vem com seis ovos e ela precisa de oito ovos. Ressalte que ela pode retirar quantos ovos quiser de cada cartela, contanto que forme oito ovos, ou seja, podem ser quatro ovos de uma cartela e quatro de outra, ou cinco de uma e três de outra, mas que independente da disposição dos ovos retirados, a fração e o número misto dos ovos utilizados para a receita serão os mesmos, ou seja, oito sextos ou 1 inteiro e dois sextos.
Mediante a equivalência de frações, cada cartela pode ser dividida em três partes e utilizar uma inteira mais uma parte da outra, chegando ao número misto 1 inteiro e um terço ou à fração quatro terços.
Propósito: Identificar frações maiores que a unidade, representando tanto na forma mista como na fracionária.
Discuta com a turma:
- Nas soluções apresentadas anteriormente, foi utilizada mais ou menos de uma cartela de ovo?
- Quantos ovos há em cada cartela?
- Quantos ovos Maria utilizou?
- Apenas uma cartela foi suficiente para atender à quantidade que Maria precisava?
- Que frações podem representar a quantidade de ovos que Maria necessita?
- Estas frações representam mais ou menos de um inteiro?
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Sistematização
Tempo sugerido: 5 minutos.
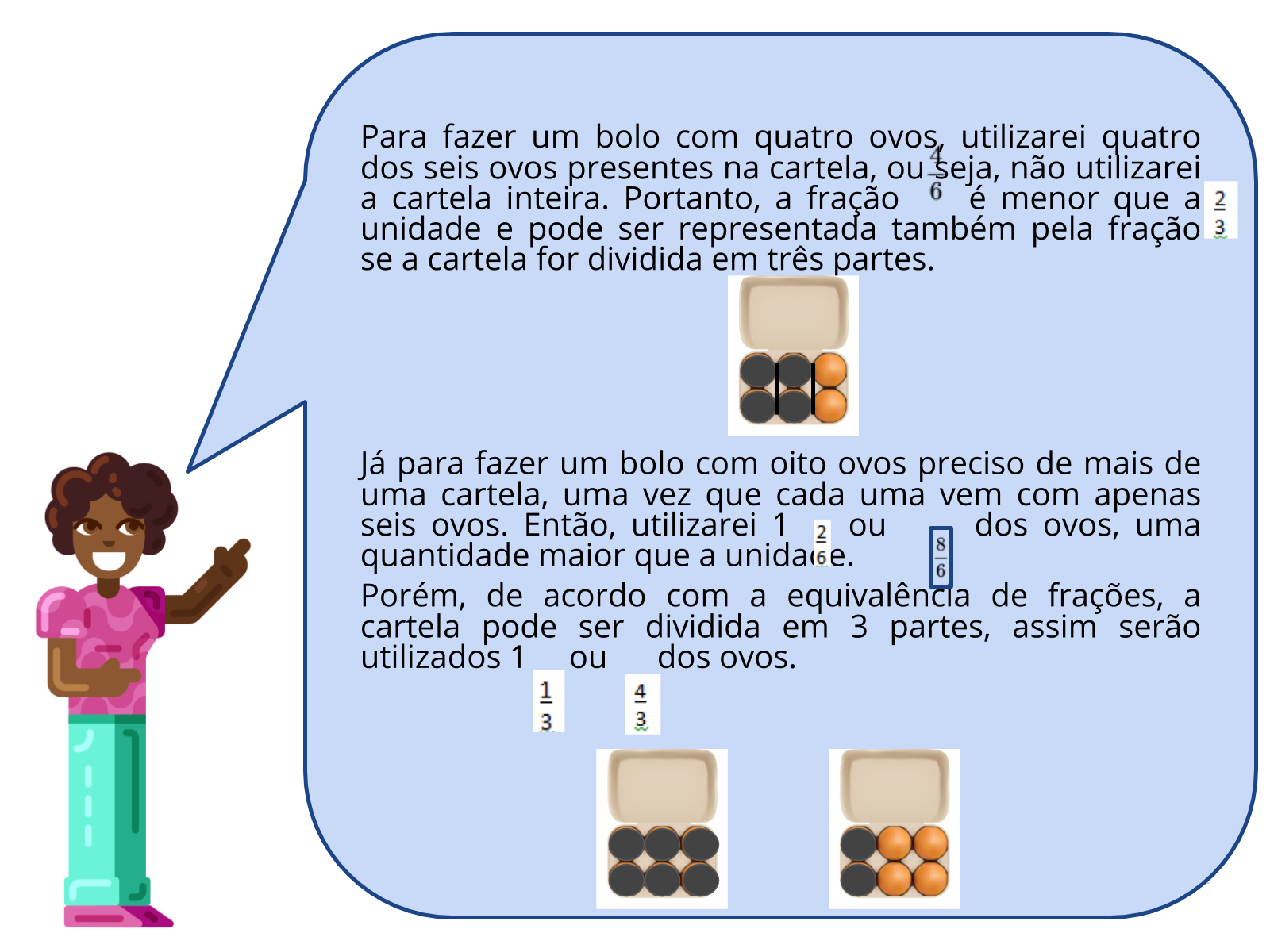
Orientação: Para sistematizar os conhecimentos trabalhados, é necessário retomar a resposta obtida para verificar como identificaram a fração maior e a fração menor que a unidade.
Propósito: Sintetizar as maneiras de se identificar frações maiores e menores que a unidade em diferentes contextos.
Discuta com a turma:
- A primeira fração apresentada precisou de quantas cartelas de ovo para representá-la? E a segunda?
- Como diferenciamos frações maiores e menores que a unidade?
- A fração 4/6 pode ser representada pela fração ?? Por quê?
- Por que a fração 8/6 pode ser representada também pela fração 1 inteiro e 2/6?
Encerramento

Tempo sugerido: 4 minutos.
Orientação: Oriente os alunos a se lembrar do que foi trabalhado na atividade principal e relatarem, e poucas palavras, a que conclusão chegaram ao resolvê-la. Lembre a eles que a unidade pode ser um único objeto ou coleção deles, como a cartelas de ovos apresentada na atividade.
Propósito: Consolidar o conceito de frações maiores e menores que a unidade.
Discuta com a turma:
- Quantas cartelas de ovo foram necessárias para representar a fração 4/6? E para representar a fração 8/6?
- Qual a diferença entre frações maiores e menores que o inteiro?
Raio X
Tempo sugerido: 10 minutos.
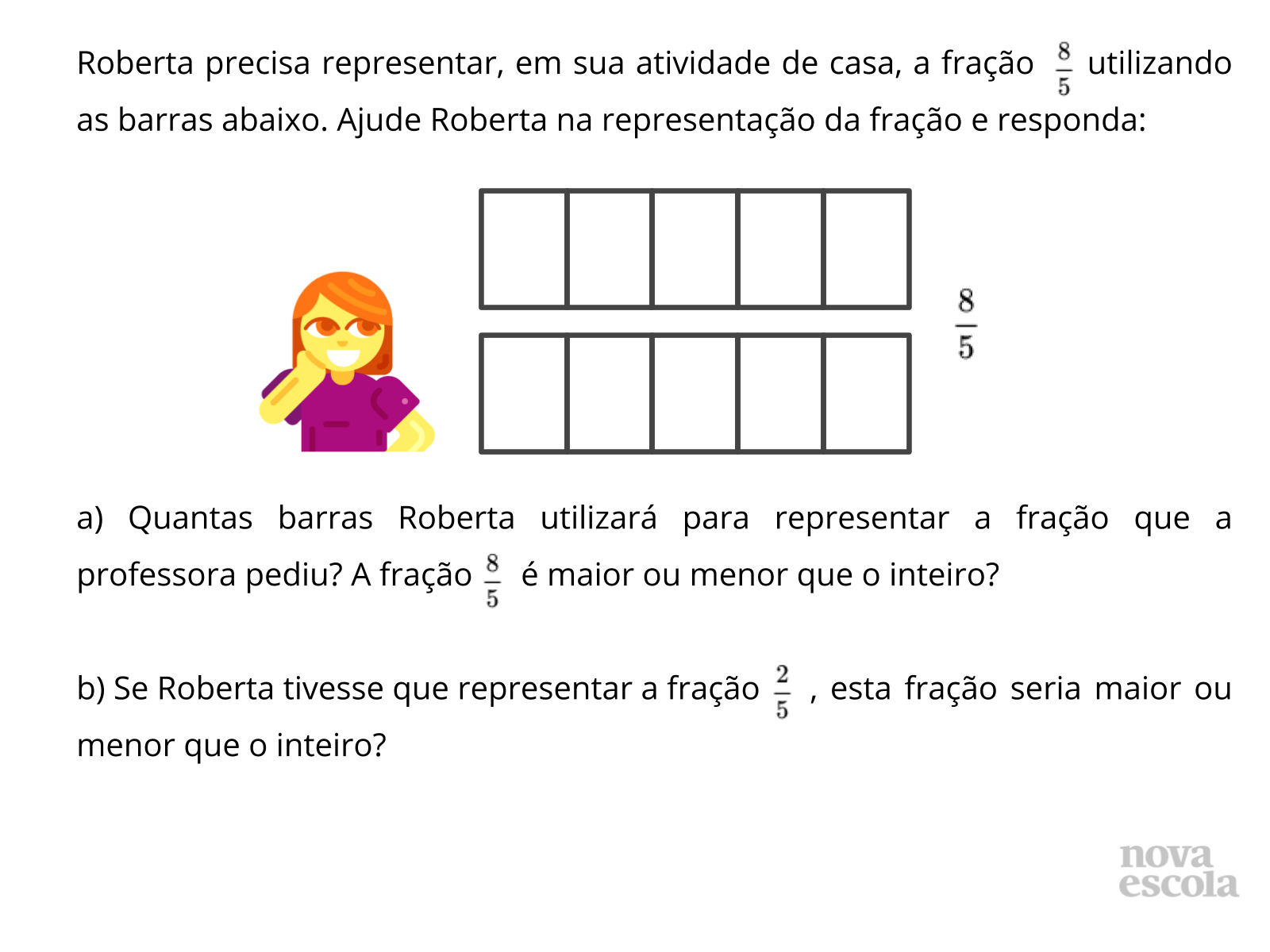
Orientação: Para facilitar a realização da atividade, sala de aula deve estar organizada em semicírculo. Em seguida, peça que, individualmente, os alunos leiam a atividade e a realizem, utilizando lápis de cor para diferenciar as frações, uma vez que eles podem desejar representar, por meio de um desenho, a comparação que fizeram. Em seguida, peça que os alunos que compartilhem com o colega ao lado suas soluções e modos de representar a atividade. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
Propósito: Verificar se os alunos compreenderam a identificação de frações maiores e menores que a unidade.
Discuta com a turma:
- Como você representou as frações da questão?
- Quantas figuras Roberta utilizou para cada fração?
- A sua resposta foi igual à de seu colega? Por quê?
Materiais complementares:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.