Resumo da aula
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar a proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo
- Tempo sugerido: 2 minutos
- Orientação: Apenas leia o objetivo para a turma, ressaltando a importância da colaboração dos alunos para atingir as metas estabelecidas para a aula.
Retomada
Tempo sugerido: 4 minutos
Orientação: Esta atividade pode ser realizada em duplas. Comece o aquecimento lembrando aos alunos que, nos números decimais, a vírgula separa os números inteiros das unidades menores que os inteiros. Além disso, a régua pode apresentar duas unidades de medida: os centímetros e os milímetros e dentro de cada centímetro há dez milímetros. Portanto, meio centímetro tem cinco milímetros (representado pelo tracinho maior que existe entre os dois números naturais na reta numerada). O que está antes da metade está próximo à medida anterior e o que está depois da metade está próximo à medida seguinte.
Propósito: Retomar o conceito de representação decimal na reta numerada a partir de objetos do cotidiano dos alunos.
Discuta com a turma:
- Para que serve a régua?
- Que unidades de medida vocês encontram na régua? Qual a maior e qual a menor delas?
- Quantos milímetros há em cada centímetro?
- O que representa o tracinho maior que se encontra entre dois números inteiros na régua?
- Entre quais centímetros se encontra a medida marcada pela professora de Carolina?
- Qual a medida marcada pela professora de Carolina?
- Como lemos o número decimal que representa a medida que a professora marcou?
Atividade principal
Tempo sugerido: 15 minutos (slides 4, 5, 6 e 7).
Orientação: Organize os alunos em duplas. Reforce com os alunos que os números decimais estão relacionados a frações de base dez. Assim, os números 1,2 e 1,3, são decimais e representam respectivamente, um inteiro e dois décimos, e um inteiro e três décimos. Os décimos são obtidos de cada unidade ao dividi-la em 10 partes menores. Cada décimo pode ser dividido em 10 partes menores que correspondem aos centésimos.
Na régua, a representação dos inteiros corresponde à medida de centímetros e, ao dividi-lo em 10 partes, temos a representação dos milímetros. Se necessário, deixe que os alunos manuseiem a régua para exemplificar que, a cada dez milímetros temos um centímetro, que é uma unidade maior que o milímetro. É importante ressaltar que entre 1,2 e 1,3 existem infinitos números decimais (veja mais detalhes no Guia de Intervenções).
Propósito: Representar o número decimal na reta numerada.
Discuta com a turma:
- Para que serve a vírgula no número decimal?
- O que representam os números que estão à esquerda da vírgula? E à direita?
- Você poderia citar alguns números que existem entre 1,2 e 1,3? E entre 1,5 e 1,6?
Materiais complementares:
Atividade principal
Resolução da atividade principal
Guia de intervenção
Atividade principal
Tempo sugerido: 15 minutos (slides 4, 5, 6 e 7).
Orientação: Peça aos alunos que marquem dez pontinhos entre os números 1,2 m e 1,3 m e entre os números 1,5 m e 1,6 m. Assim, ficará mais fácil identificar a medida do local em que caíram os discos que os meninos lançaram. Deixe que os alunos resolvam o problema em duplas. Se necessário, faça a reta numerada no chão e peça para os alunos marcarem nela alguns números que existem entre 1,2 m e 1,3 m, ressaltando que há infinitos números decimais entre eles. Espera-se que os alunos percebam que, os números a partir de 1,25 m, passaram da metade entre 1,2 m e 1,3 m e, portanto, estão mais próximos a 1,3 m. Assim, como antes da metade estão mais próximos de 1,2 m.
Discuta com a turma:
- Quantos números existem entre 1,2 m e 1,3 m? Você poderia citar alguns números?
- Que número representa a metade da distância entre 1,2 m e 1,3 m?
- Quais números estão próximos a 1,3 m?
- Em que locais pode ter caído o disco de Cauê?
- Você poderia citar alguns números que existem entre 1,4 m e 1,5 m? Quais estão próximos a 1,4 m?
- Em que locais pode ter caído o disco de Guilherme?
- Quem jogou o disco mais longe?
Atividade principal
Tempo sugerido: 15 minutos (slides 4, 5, 6 e 7).
Orientação: Lembre aos alunos que existem diferentes objetos utilizados para medir comprimento. Se possível, deixe que vejam uma trena e as medidas que ela apresenta para familiarizarem-se com o objeto e facilitar a compreensão da atividade. Peça para que vejam quantos tracinhos há entre um número e outro, comparando com a régua. Ressalte que a trena está apresentando as medidas em centímetros, e não em metros.
Propósito: Identificar o número decimal na reta numerada.
Discuta com a turma:
- Para que serve a trena?
- Os números que estão apresentados nela estão em metros ou centímetros?
- O que representam os tracinhos que estão entre os números identificados na trena?
- O tracinho azul está entre quais números? Mais próximo de qual deles?
- Quantos tracinhos há entre o número 48 e o tracinho azul?
- Qual das unidades se refere à altura do cachorrinho de Cauê?
- Qual a medida da altura do cachorrinho de Cauê? Usaremos a vírgula nesse número? Por quê?
Atividade principal
Tempo sugerido: 15 minutos (slides 4, 5, 6 e 7).
Orientação: Deixe que os alunos utilizem a régua para realizar esta atividade. Peça para que eles verifiquem quantos espaços há entre um centímetro e outro. Explique que estes espaços são chamados de milímetro e que a cada um centímetro existem dez milímetros, ressalvando as abreviaturas (cm = centímetro e mm = milímetro). Então, 10 mm = 1 cm, 20 mm = 2 cm, 100 mm = 10 cm, 150 mm = 15 cm. Como Roberta precisa de 155 mm, então, ela precisa de 15 cm + 0,5 cm, ou seja, 15,5 cm.
Propósito: Identificar o número decimal na reta numerada.
Discuta com a turma:
- Qual é o tamanho do barbante que Roberta precisa ?
- A medida que Roberta apresentou está em qual unidade de medida? E a régua?
- Quantos milímetros há em cada centímetro?
- Quantos centímetros há em 150 milímetros? E em 155 milímetros?
- O barbante que Roberta cortou termina entre quais números da régua? Quantos milímetros ele tem?
Discussão da solução
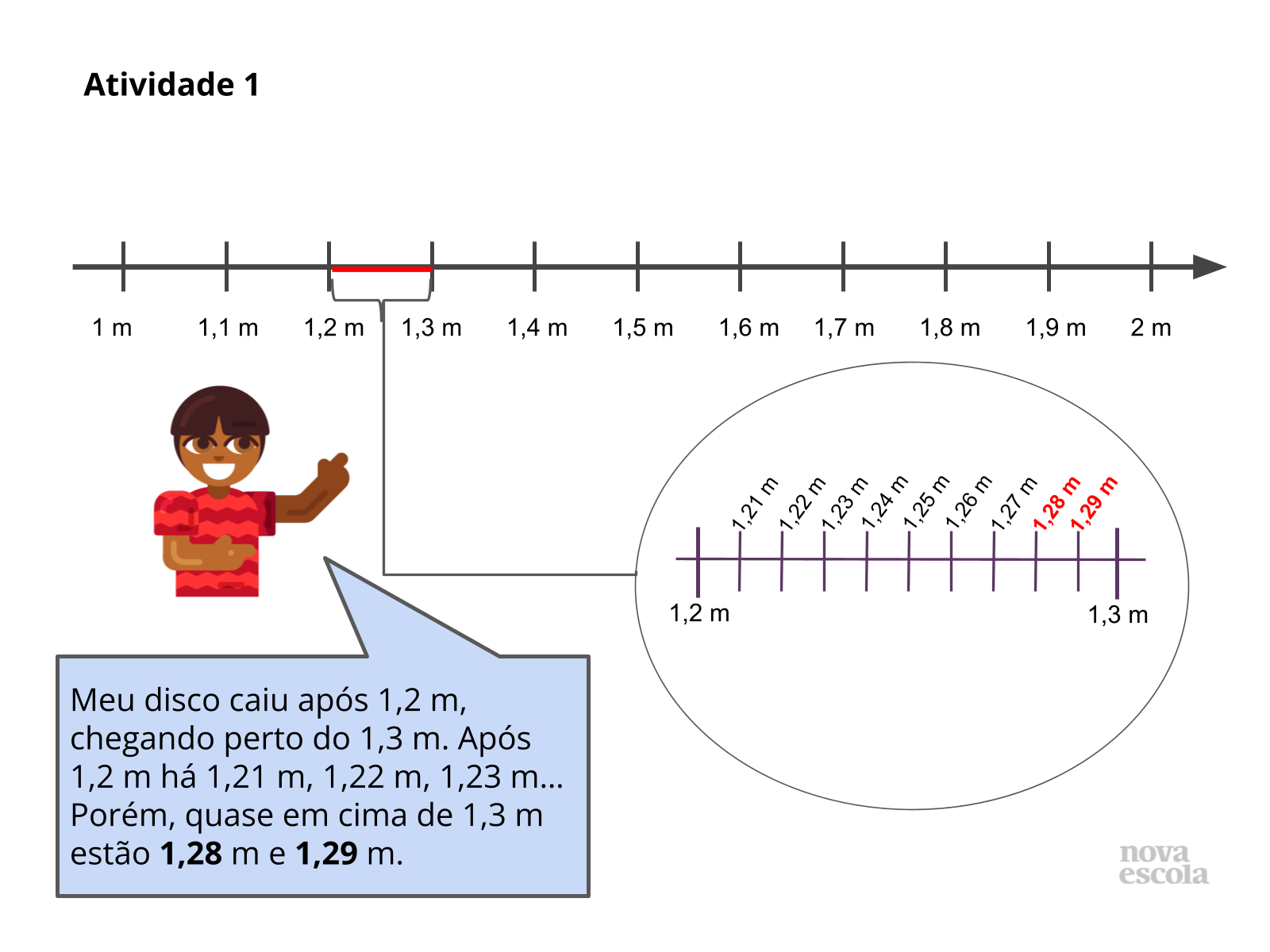
Tempo sugerido: 15 minutos (slides 8, 9, 10 e 11).
Orientação: Para esta atividade, deixe que os alunos manuseiem a régua, verificando que entre dois números inteiros existem unidades menores. Assim, será possível identificar quais números mais se aproximam de 1,3 m. Lembre a eles que, neste caso, após a vírgula teremos a representação dos décimos e dos centésimos. Professor(a), o guia abordará melhor quanto aos infinitos decimais que existem entre dois números naturais.
Propósito: Apresentar soluções para a representação de números decimais na reta numerada.
Discuta com a turma:
- O número que representa o local em que o disco de Cauê caiu está entre quais números? Mais próximo de qual deles?
- Você poderia citar alguns números que existem entre 1,2 e 1,3 m?
- Quais são os números que estão mais próximos a 1,3 m? Por quê?
Discussão da solução
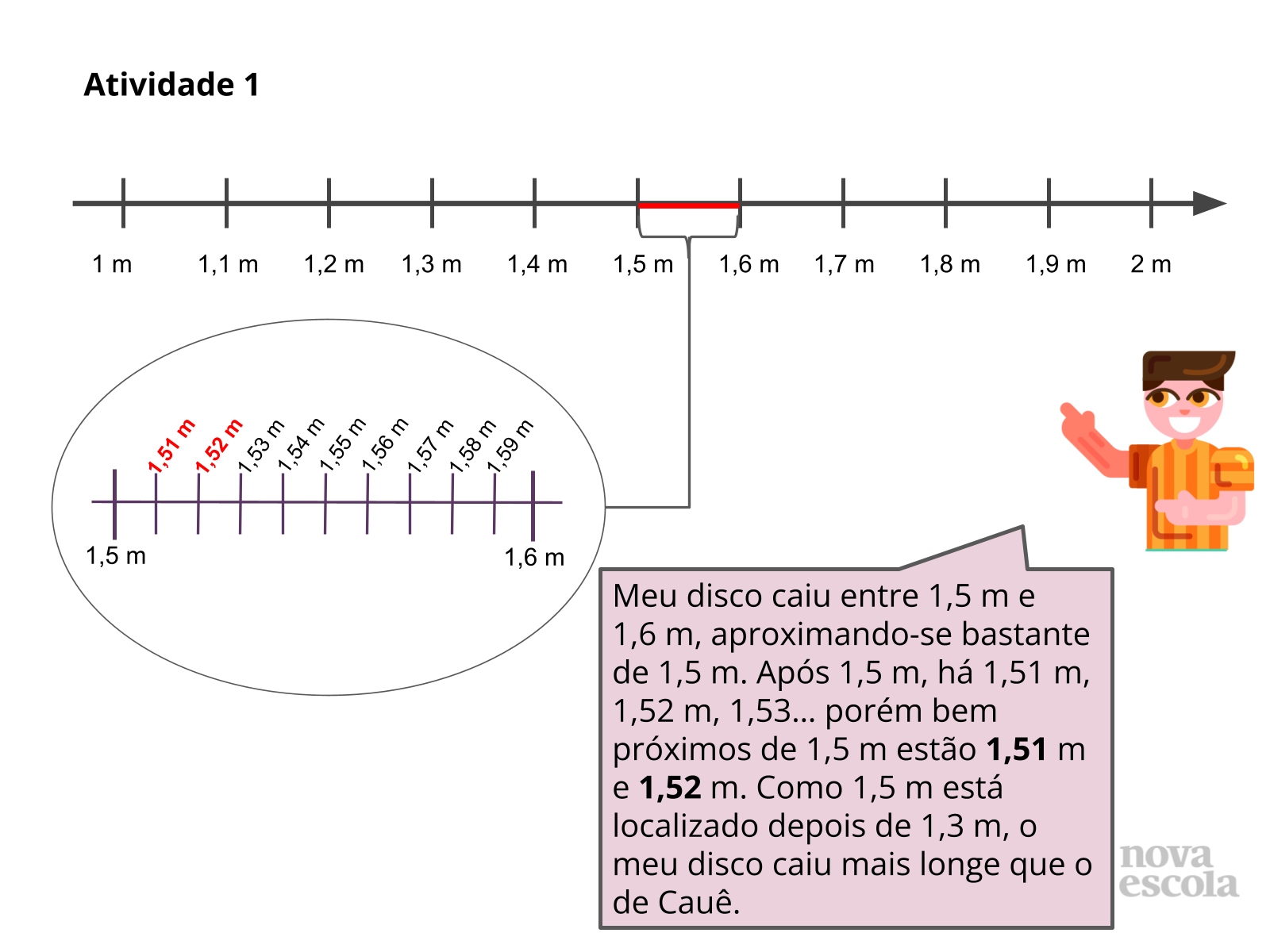
Tempo sugerido: 15 minutos (slides 8, 9, 10 e 11).
Orientação: Se necessário, os alunos podem continuar manuseando a régua para se recordarem das unidades menores, como os milímetros. Reforce novamente a eles que, entre 1,5 e 1,6 m existem outros números e que, neste caso, indicaremos os que têm representação decimal com décimos e centésimos.
Propósito: Apresentar soluções para a representação de números decimais na reta numerada.
Discuta com a turma:
- O número que representa o local em que o disco de Guilherme caiu está entre quais números? Mais próximo de qual deles?
- Você poderia citar alguns números que existem entre 1,5 e 1,6?
- Quais são os números que estão mais próximos a 1,5? Por quê?
- Quais são os números que estão “bem próximos a” 1,5? Por quê?
Discussão da solução
Tempo sugerido: 15 minutos (slides 8, 9, 10 e 11).
Orientação: Se houver a possibilidade de levar uma trena para a sala de aula, deixe os alunos manusearem-na para terem uma visão concreta do objeto apresentado. Ressalte que a trena apresenta as medidas em centímetros e que as unidades menores que os centímetros são os milímetros.
Propósito: Apresentar soluções para a identificação de números decimais na reta numerada.
Discuta com a turma:
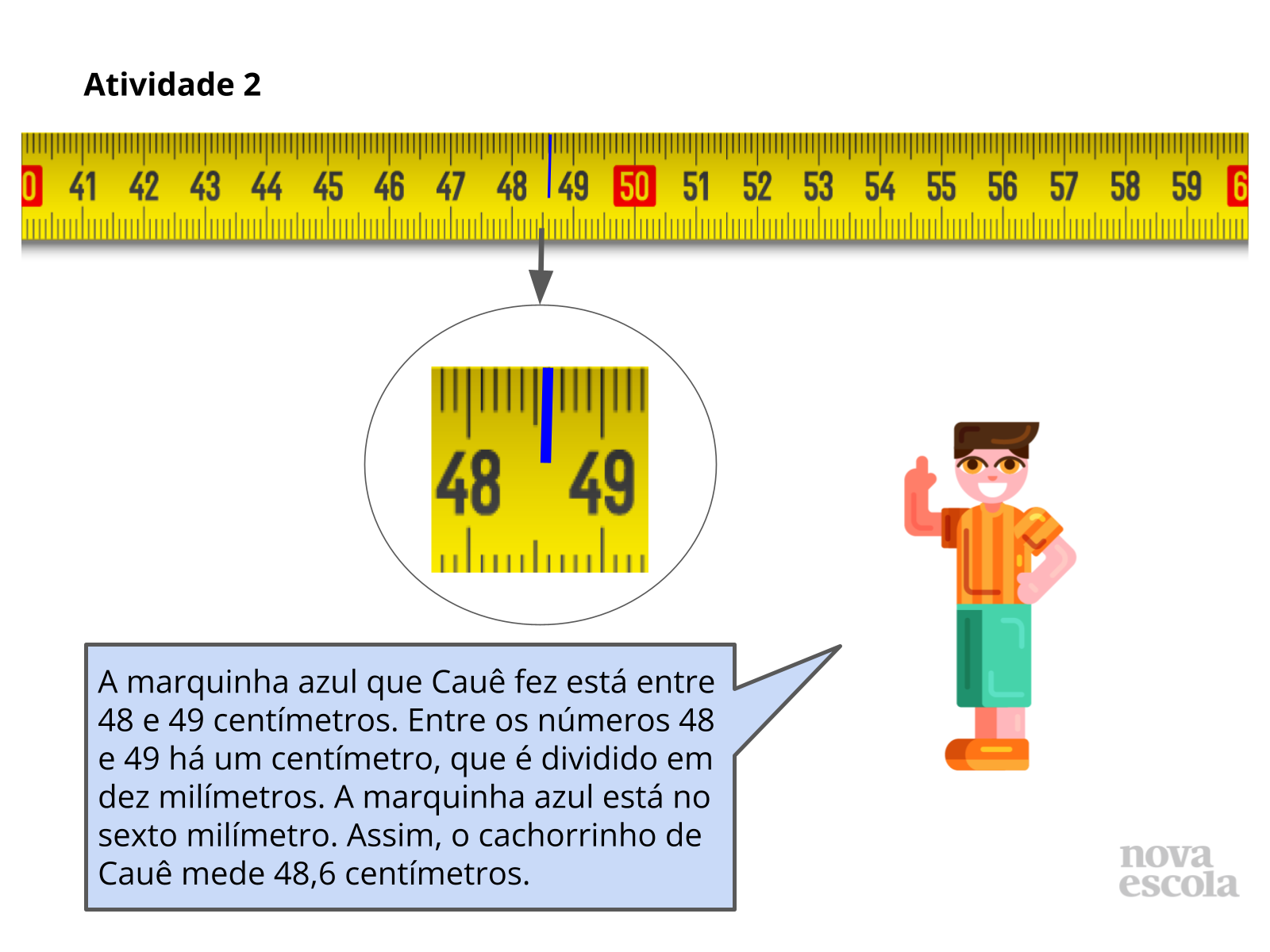
- Que unidade de medida é representada pelos números da trena? O que representam os tracinhos entre eles?
- Quantos tracinhos existem entre um número e outro?
- Entre quais números está a marquinha azul?
- Em qual dos tracinhos está a marquinha azul?
- Qual a medida da altura do cachorrinho de Cauê?
Discussão da solução
Tempo sugerido: 15 minutos (slides 8, 9, 10 e 11).
Orientação: Utilizando uma régua e com um pedaço de barbante, os alunos conseguem visualizar melhor o tamanho do barbante. Deixe que manuseiem o material, concretizando a visão da atividade. Lembre a eles que entre dois números inteiros existem unidades menores e, neste caso, os inteiros considerados são os centímetros.
Propósito: Identificar o número decimal na reta numerada.
Discuta com a turma:
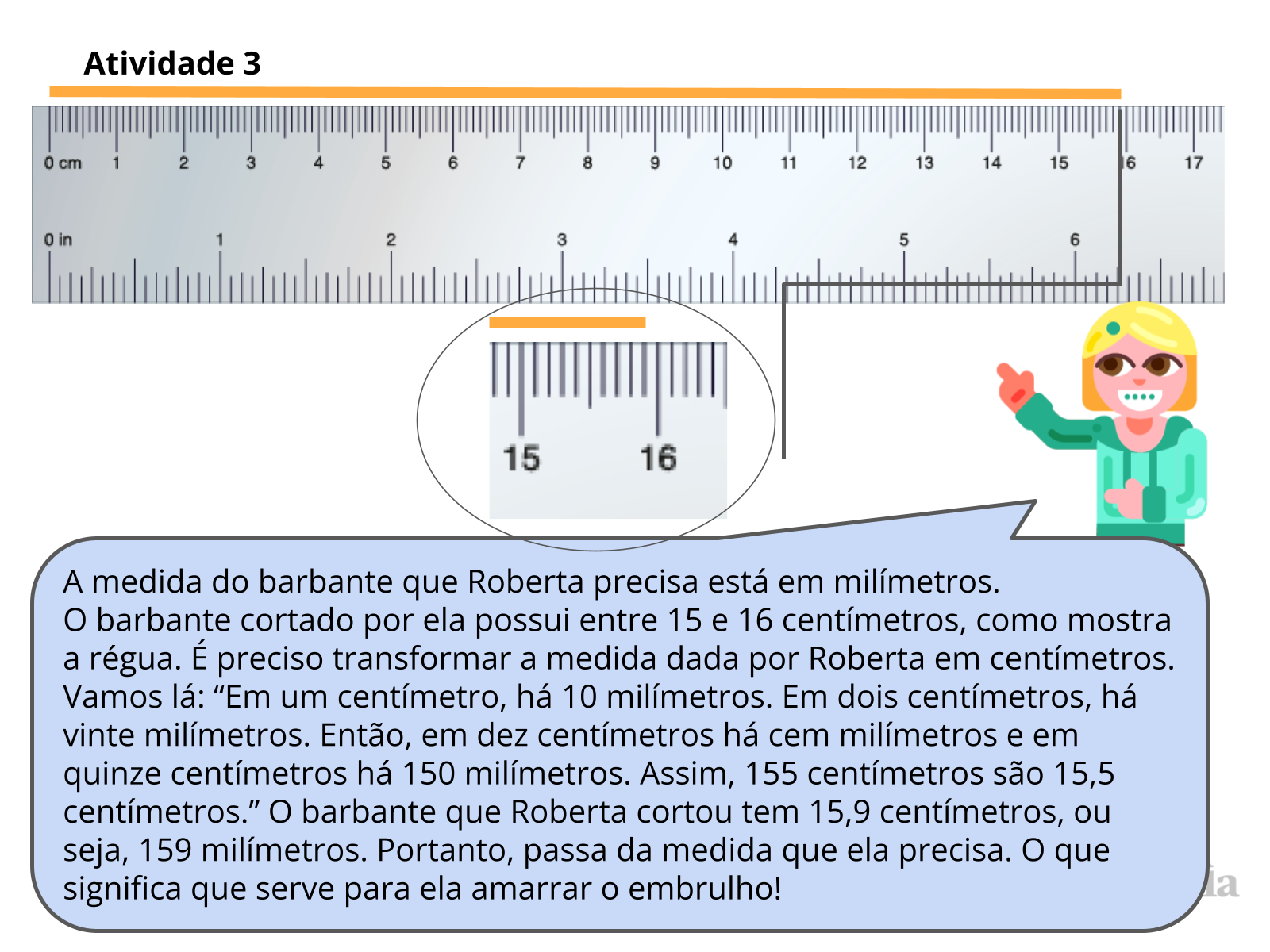
- O barbante que Roberta cortou é maior ou menor que 15 centímetros?
- Para medir o tamanho que Roberta precisa,o barbante deveria terminar exatamente em que local? Onde termina o que ela cortou?
- Quanto mede o barbante cortado por Roberta? É o suficiente para ela amarrar o embrulho? Por quê?
Encerramento
Tempo sugerido: 4 minutos
Orientação: Comece o encerramento lembrando aos alunos que, nos números decimais, a vírgula separa os números inteiros das unidades menores que os inteiros e que a régua apresenta unidades de medida como os centímetros e os milímetros. É importante observar que dentro de cada centímetro há dez milímetros. Faça a discussão coletivamente.
Propósito: Compreender como representar os números decimais na reta numerada.
Discuta com a turma:
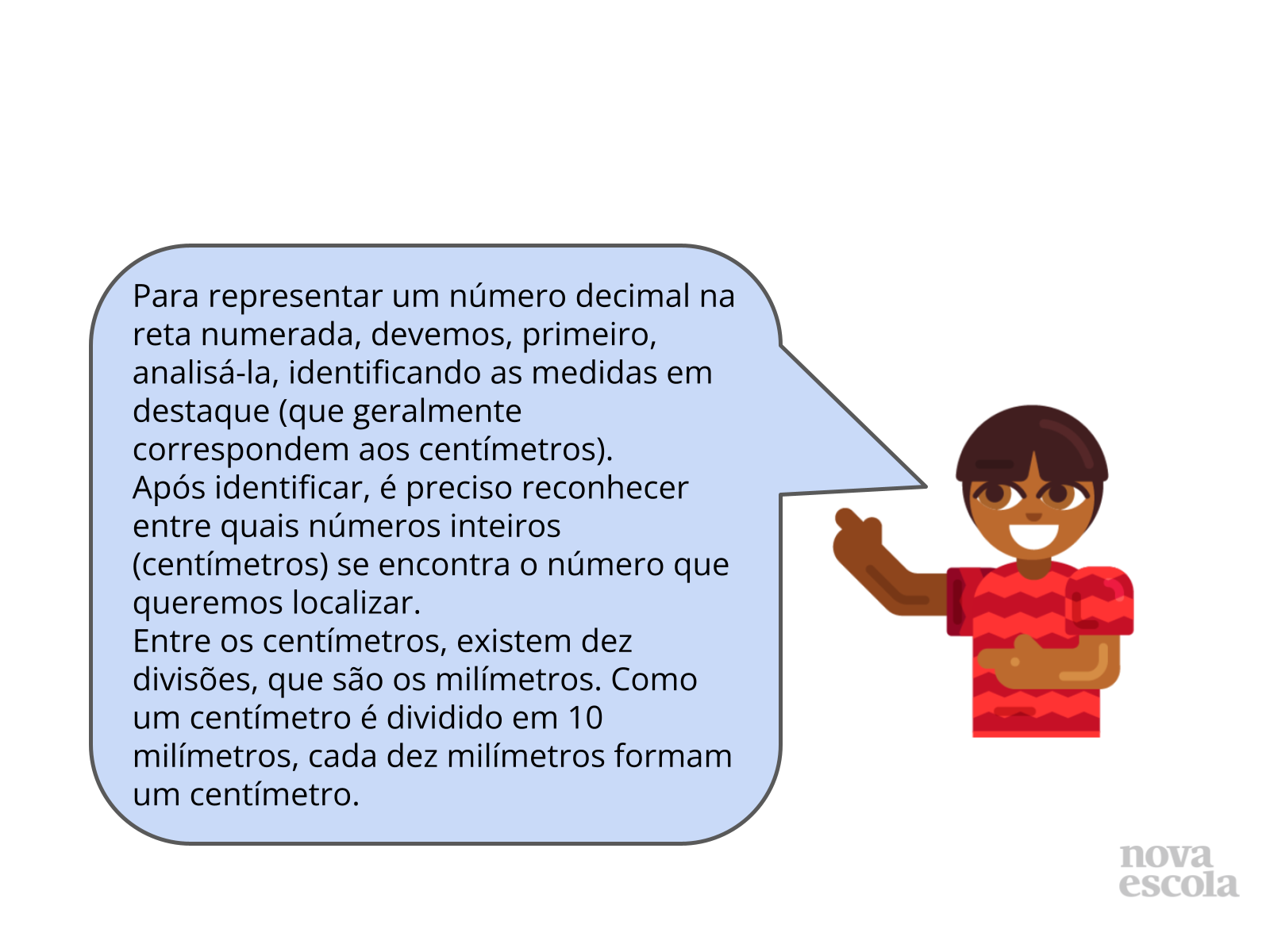
- O que separa a parte inteira da parte decimal de um número?
- O que devemos observar primeiro ao representar um número na reta numérica: a parte inteira ou decimal?
- Quantos décimos existem entre um inteiro (metro ou centímetro)?
Raio-X
Tempo sugerido: 10 minutos.
Orientação: Organize os alunos em duplas. Peça que cada um faça a sua atividade e, depois, compare a resposta com a do colega ao lado. Lembre aos alunos que a medida que vem após os centímetros, ou seja, após a vírgula, representa os milímetros.
Propósito: Verificar se os alunos compreenderam a representação dos números decimais na reta numerada.
Discuta com a turma:
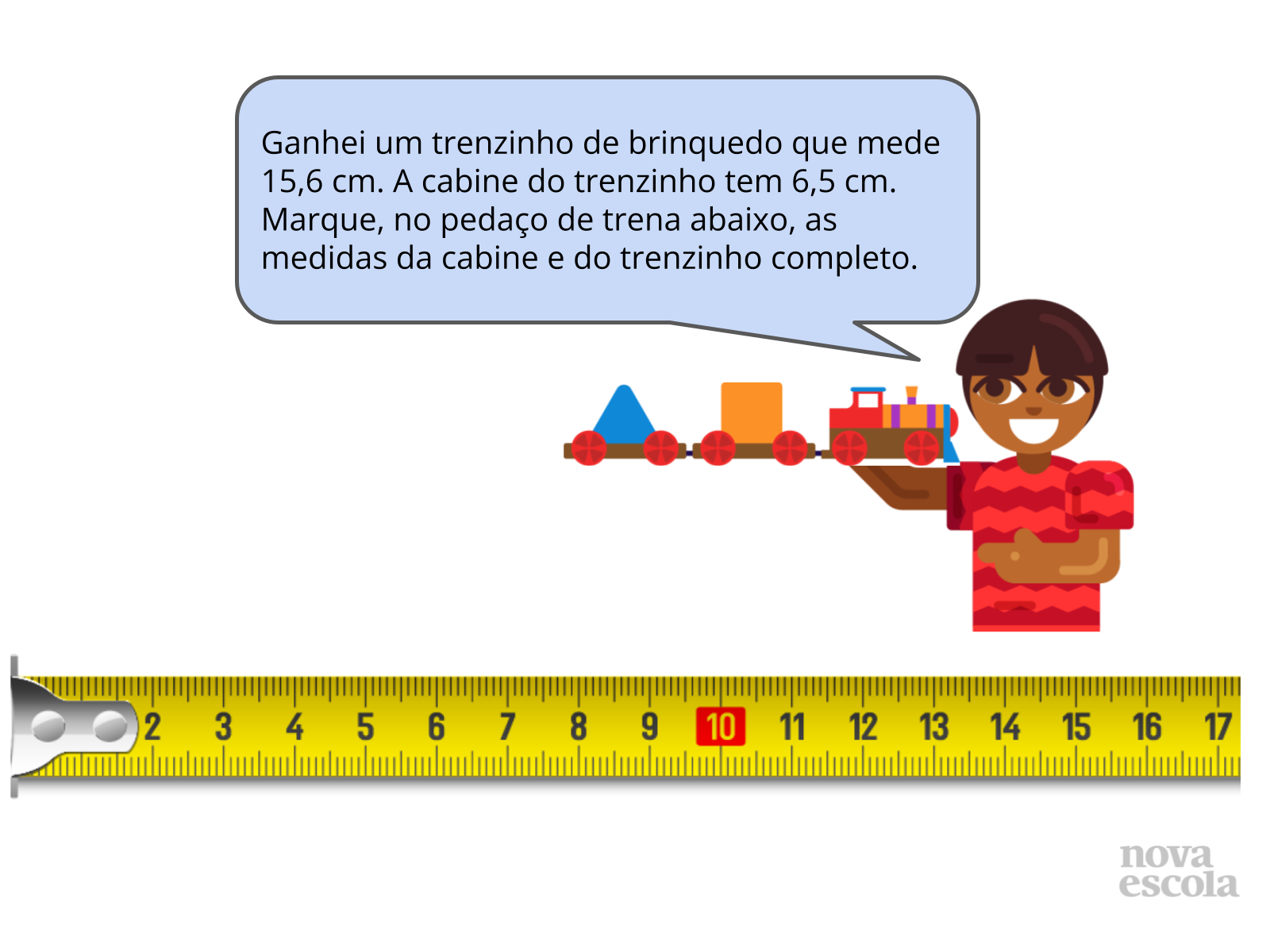
- Como se chama a medida menor que o centímetro?
- Quantos centímetros e quantos milímetros possui o trenzinho? E apenas a cabine?
- Entre quais números você marcou cada medida? Por quê?
Materiais complementares:
Atividade raio-x
Atividade complementar
Resolução do raio-x
Resolução da atividade complementar
