Resumo da aula
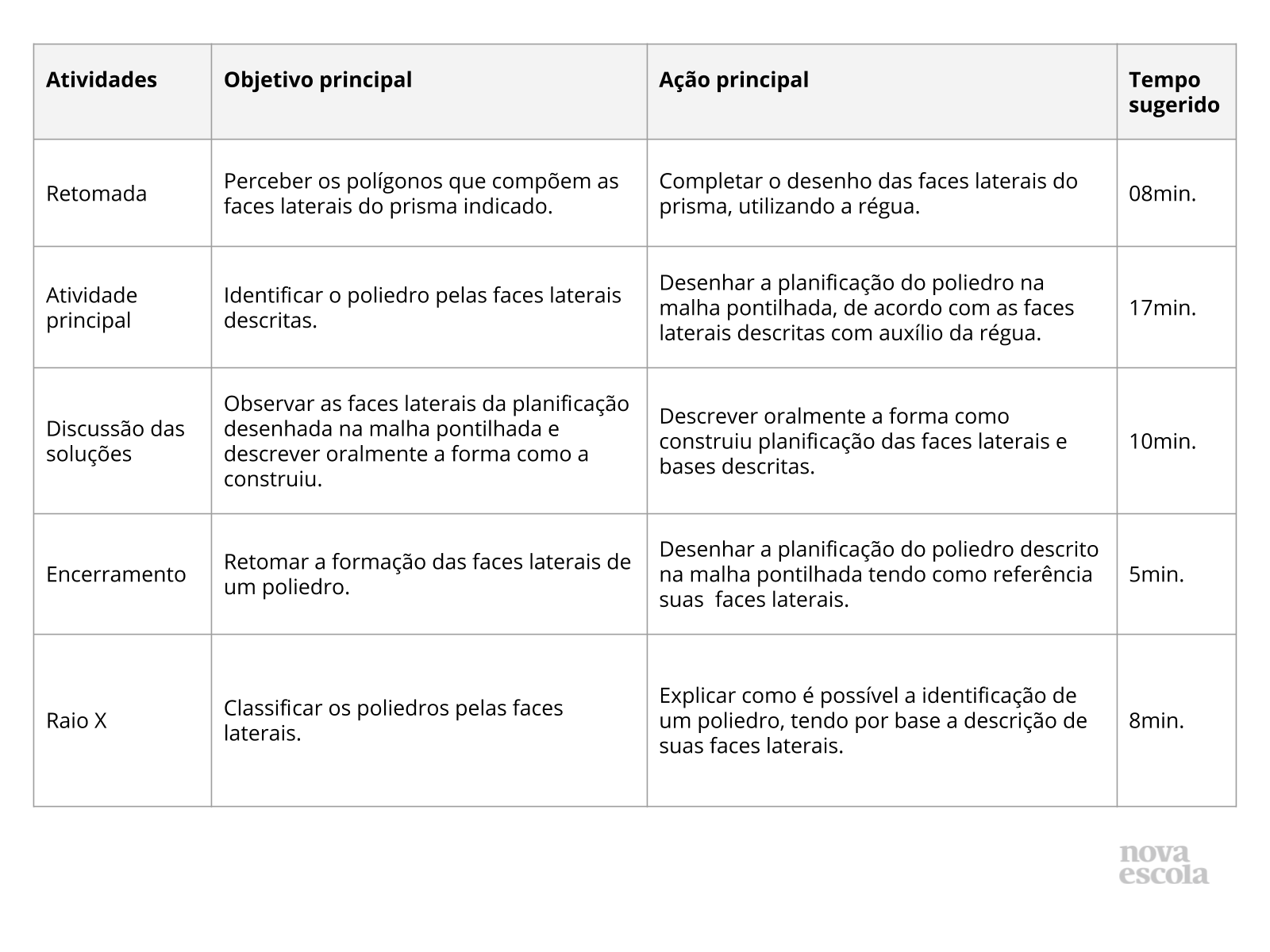
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
OBJETIVO

Tempo sugerido: 2 minutos.
Orientação: Exponha o objetivo para a classe e leia junto com eles.
Propósito: Apresentar o objetivo à turma.
Discuta com a turma:
- Discuta com os alunos os termos “superfícies laterais”, pois é importante que resgatem o conhecimento sobre as representações poligonais dos poliedros (tridimensionais), bem como as características que os compõem para o bom desenvolvimento da atividade principal.
RETOMADA
Tempo sugerido: 08 minutos.
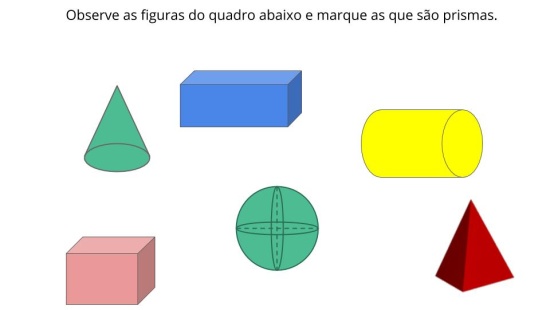
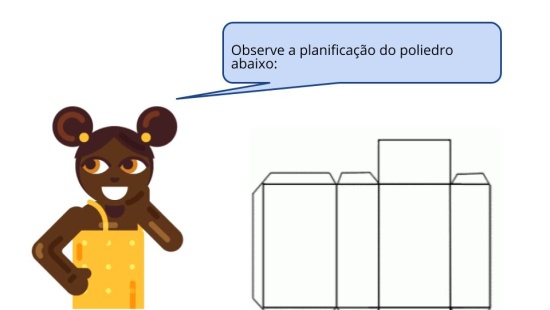
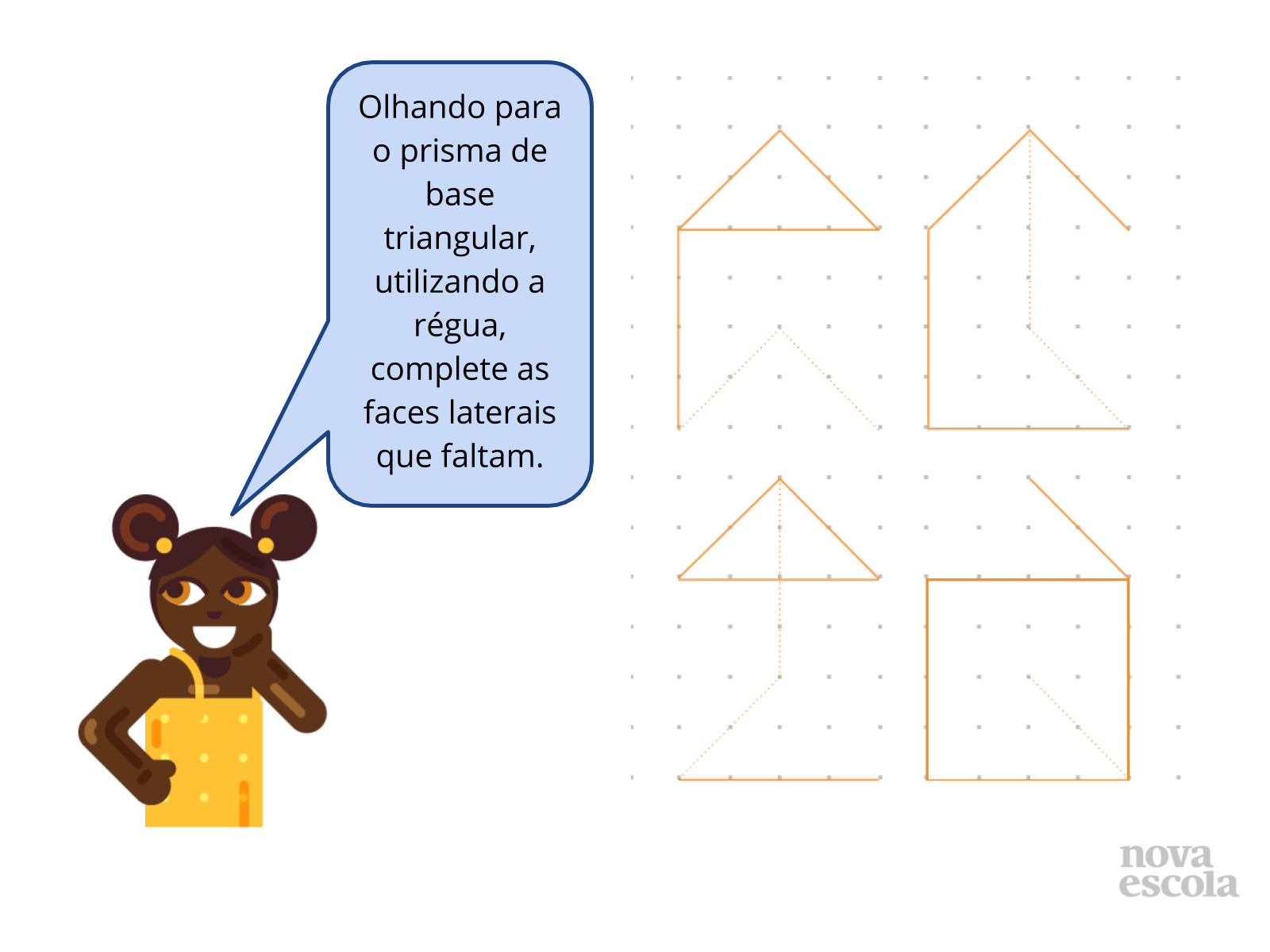
Orientações: Este é o momento de retomada de conteúdo. Esta atividade permite que os alunos, completem as partes faltantes e explorem a leitura de imagens de acordo com as faces laterais que compõem o poliedro. Verifique se ainda há alunos que não identificam as faces laterais e bases. Caso haja, retome com eles o que são faces, vértices e arestas para que tenham condições de realizar a atividade principal.
Aresta: segmento de reta onde duas faces de um poliedro se encontram; Faces: formas poligonais que delimitam um sólido; Vértice: ponto de encontro das arestas de um sólido;
Propósito: Perceber os polígonos que compõem as faces laterais do prisma indicado.
Discuta com a turma:
- “É possível completar os polígonos observando o pontilhamento de cada um deles? ”Sim. Ao observarmos as quatro formas de representação do poliedro, é possível perceber o que falta em um pela observação da construção do outro”.
- “Mediante a observação do poliedro representado, é possível identificar quantas faces laterais tem essa figura? ”Sim. O poliedro apresenta três faces laterais retangulares e duas bases triangulares que também são faces, porém não laterais”;
Material Complementar:
Atividade de retomada
Resolução da atividade de retomada
ATIVIDADE PRINCIPAL

Tempo sugerido: 17 minutos.
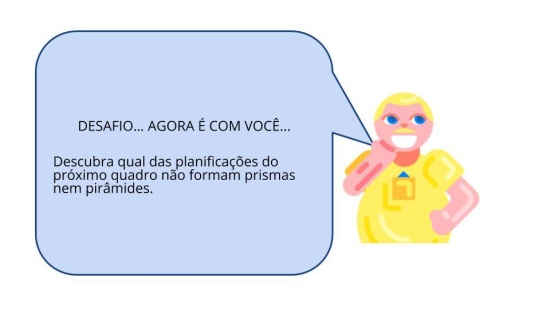
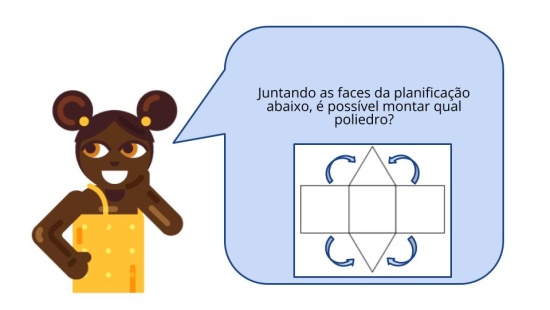
Orientações: Essa atividade foi realizada para que os alunos identifiquem os poliedros utilizando outro foco de observação, as faces laterais. É importante que leia com os alunos e discuta as hipóteses de poliedros possíveis pelas faces laterais e bases descritas. A princípio os alunos podem verbalizar que faltam informações para a descoberta. Neste momento, peça aos alunos que desenhem as faces laterais poligonais para que visualizem a possibilidade da construção planificada da figura descrita.
Propósito: Identificar e desenhar o poliedro pelas faces laterais descritas.
Discuta com a turma:
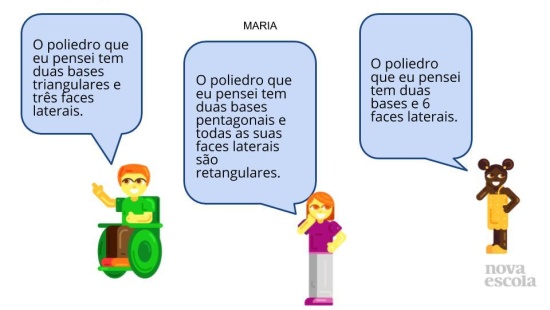
- É possível identificar o poliedro pela descrição das faces laterais? “É possível que se identifique o poliedro pelas faces laterais, pois sabemos a quantidade e todas as faces são retangulares o que caracteriza o poliedro como prisma”.
- Quando pensamos no poliedro, pensamos o mesmo no formato tridimensional. É possível planificar o poliedro por meio da imagem tridimensional formada mentalmente? “Sim, é possível, porém como trata-se de um plano de ampliação o aluno precisa trazer como repertório a vivência e exploração de prismas tridimensionais e planificados”.
- Qual poliedro está descrito por meio das faces laterais citadas? “O poliedro descrito é o prisma hexagonal por conter seis faces retangulares e duas bases hexagonais”
Material Complementar:
Atividade principal
Resolução da atividade principal
Guia de intervenções
ATIVIDADE PRINCIPAL

Tempo sugerido: 17 minutos.
Orientações: Essa atividade foi realizada para que os alunos identifiquem os poliedros utilizando outro foco de observação, as faces laterais. É importante que leia com os alunos e discuta as hipóteses de poliedros possíveis pelas faces laterais e bases descritas. A princípio os alunos podem verbalizar que faltam informações para a descoberta. Neste momento, peça aos alunos que desenhem as faces laterais poligonais para que visualizem a possibilidade da construção planificada da figura descrita.
Propósito: Identificar e desenhar o poliedro pelas faces laterais descritas.
Discuta com a turma:
- É possível identificar o poliedro pela descrição das faces laterais? “É possível que se identifique o poliedro pelas faces laterais, pois sabemos a quantidade e todas as faces são retangulares o que caracteriza o poliedro como prisma”.
- Quando pensamos no poliedro, pensamos o mesmo no formato tridimensional. É possível planificar o poliedro por meio da imagem tridimensional formada mentalmente? “Sim, é possível, porém como trata-se de um plano de ampliação o aluno precisa trazer como repertório a vivência e exploração de prismas tridimensionais e planificados”.
- Qual poliedro está descrito por meio das faces laterais citadas? “O poliedro descrito é o prisma hexagonal por conter seis faces retangulares e duas bases hexagonais”
Material Complementar
DISCUSSÃO DA SOLUÇÃO

Tempo sugerido: 10 minutos.
Orientações: Ao explicar e descrever ações importantes para que o outro compreenda o assunto da aula,essa atividade permite que os alunos exercitem a linguagem geométrica. A complexidade se dá ao repertório que os alunos precisam trazer a respeito de planificação. Cabe a você professor intervir de forma que o aluno socialize a forma que explicaria a construção planificada a outro aluno, que não teve acesso às informações desta aula. Caso os alunos apresentem muita dificuldade na elaboração, pode propor que construam essa explicação em pequenos agrupamentos, para que haja a troca e complementação de ideias. A socialização das descobertas pode ser em grupo.
Propósito: Observar as faces laterais da planificação desenhada na malha pontilhada e descrever oralmente a forma como a construiu.
Discuta com a turma:
- É possível construir na malha pontilhada a planificação do poliedro solicitado, tendo como referência principal as faces laterais? “A malha pontilhada é importante na concretização da forma planificada dos poliedros, pois nela conseguimos a precisão necessária para caracterizá-la”.
ENCERRAMENTO.

Tempo sugerido: 5 minutos.
Orientações: Este slide resume o aprendizado da aula, desta forma, é importante que o apresente aos alunos para que compreendam que a planificação do poliedro, foi possível a partir da observação das faces laterais do prisma triangular, como retomada de conteúdo. Partindo desse pressuposto, as faces laterais do prisma descrito na atividade principal, será importante para que os alunos construam a planificação por meio da imagem tridimensional do poliedro.
Propósito: Retomar a formação da planificação das faces laterais de um poliedro.
Discuta com a turma:
- Quando leram a descrição das faces laterais descritas na atividade principal foi possível imaginar o poliedro tridimensional? Como trata-se de uma plano de ampliação é possível que o aluno faça uma imagem mental do poliedro sim, pois para isso faz-se necessário repertório conceitual.
- Pela imagem mental tridimensional do poliedro é possível planifica-lo na malha pontilhada? “Sim. É possível planificar o poliedro descrito, porém faz-se necessário repertório de planificação trabalhado nas aulas conceituais”.
RAIO X.

Tempo sugerido: 8 minutos.
Orientações: Essa tarefa deve ser realizada individualmente. É importante que o aluno a realize tendo por base o aprendizado construído em sala de aula. Verifique se os alunos compreenderam a construção planificada do poliedro, partindo da caracterização de suas faces laterais. Professor, caminhe pela sala de aula e observe como os alunos resolvem a atividade e se assimilaram o conteúdo proposto na aula.
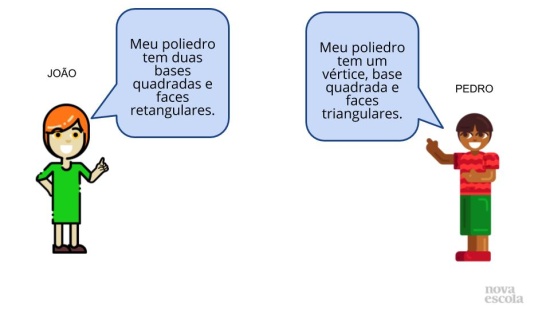
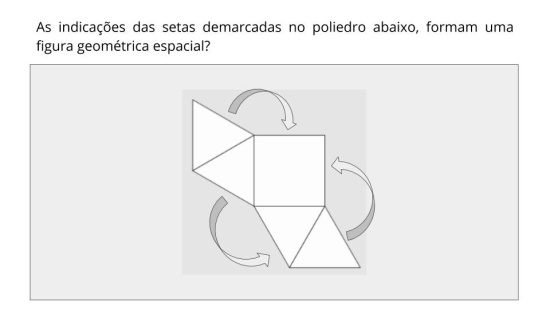
Propósito: Classificar os poliedros pelas faces laterais.
Discuta com a turma:
- É possível classificar um poliedro pelas faces laterais? “Sim, pois as faces laterais são características marcantes para a classificação dos poliedros. Sabemos que são prismas, por exemplo, pelas faces retangulares ou pirâmides pelas faces triangulares”.
Material complementar:
Atividade complementar
Atividade Raio X
Resolução da atividade complementar
Resolução do Raio X
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.