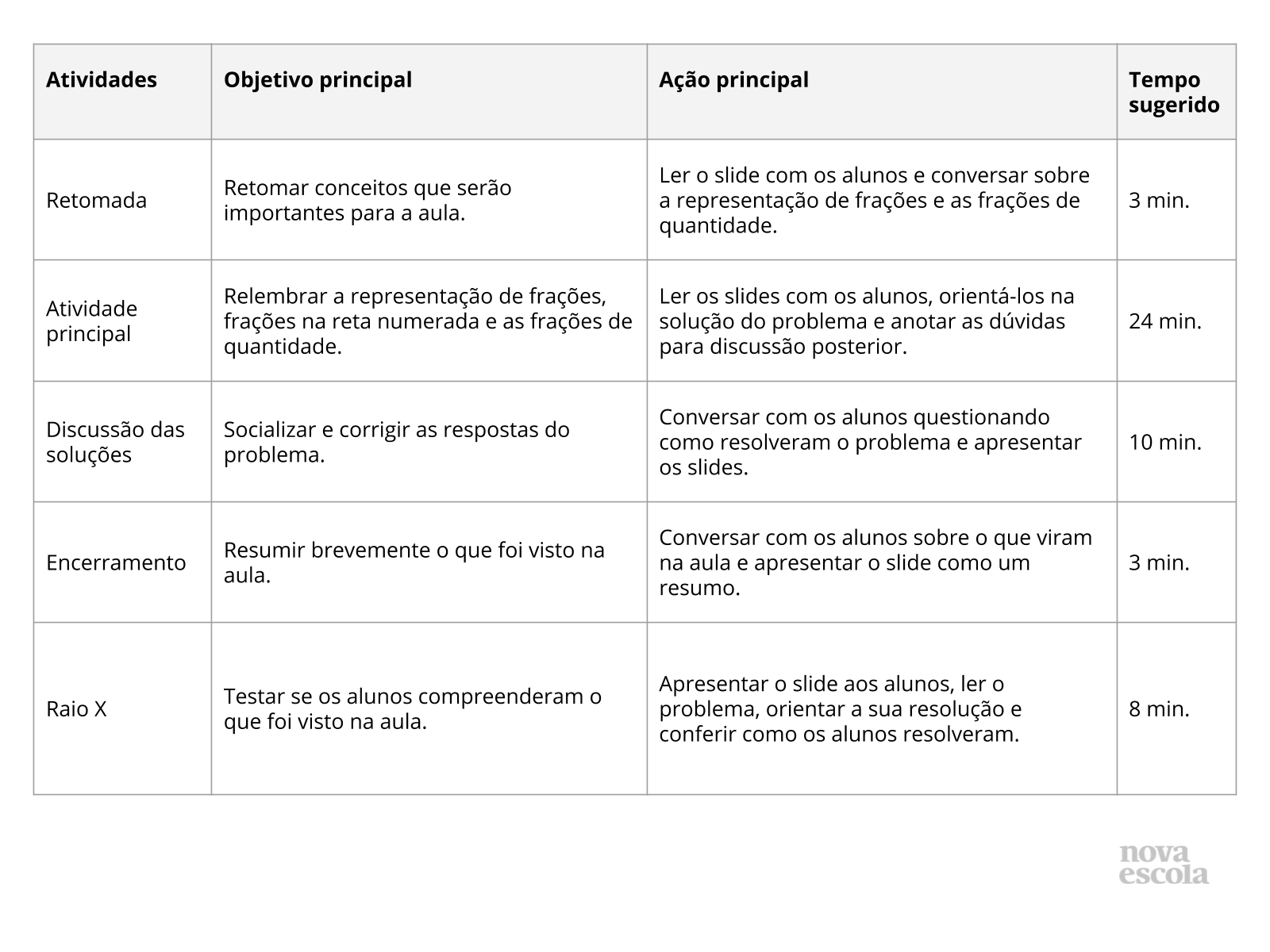
Atividade principal
Plano de Aula
Plano de aula: Calculando frações II
Plano 7 de uma sequência de 10 planos. Veja todos os planos sobre Trabalhando com Frações Unitárias
Por: Thaís Schulz
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Thaís Schulz
Mentor: Elisa Greenhalgh Vilalta
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA09 - Reconhecer as frações unitárias mais usuais (1/2, 1/3, 1/4, 1/5, 1/10 e 1/100) como unidades de medida menores do que uma unidade, utilizando a reta numérica como recurso.
Objetivos específicos
Calcular frações de quantidade, envolvendo meios, terços, quartos, quintos e sextos.
Conceito-chave
Cálculo de frações
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Materiais para a representação das frações (barbante, papel colorido, isopor, discos de pizza, marcadores, giz e lápis coloridos, etc.);
- Réguas (suficientes para a turma);
- Barbante ou lã.
Habilidades BNCC:
Objetivos de aprendizagem
Calcular frações de quantidade, envolvendo meios, terços, quartos, quintos e sextos.
Resumo da aula
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
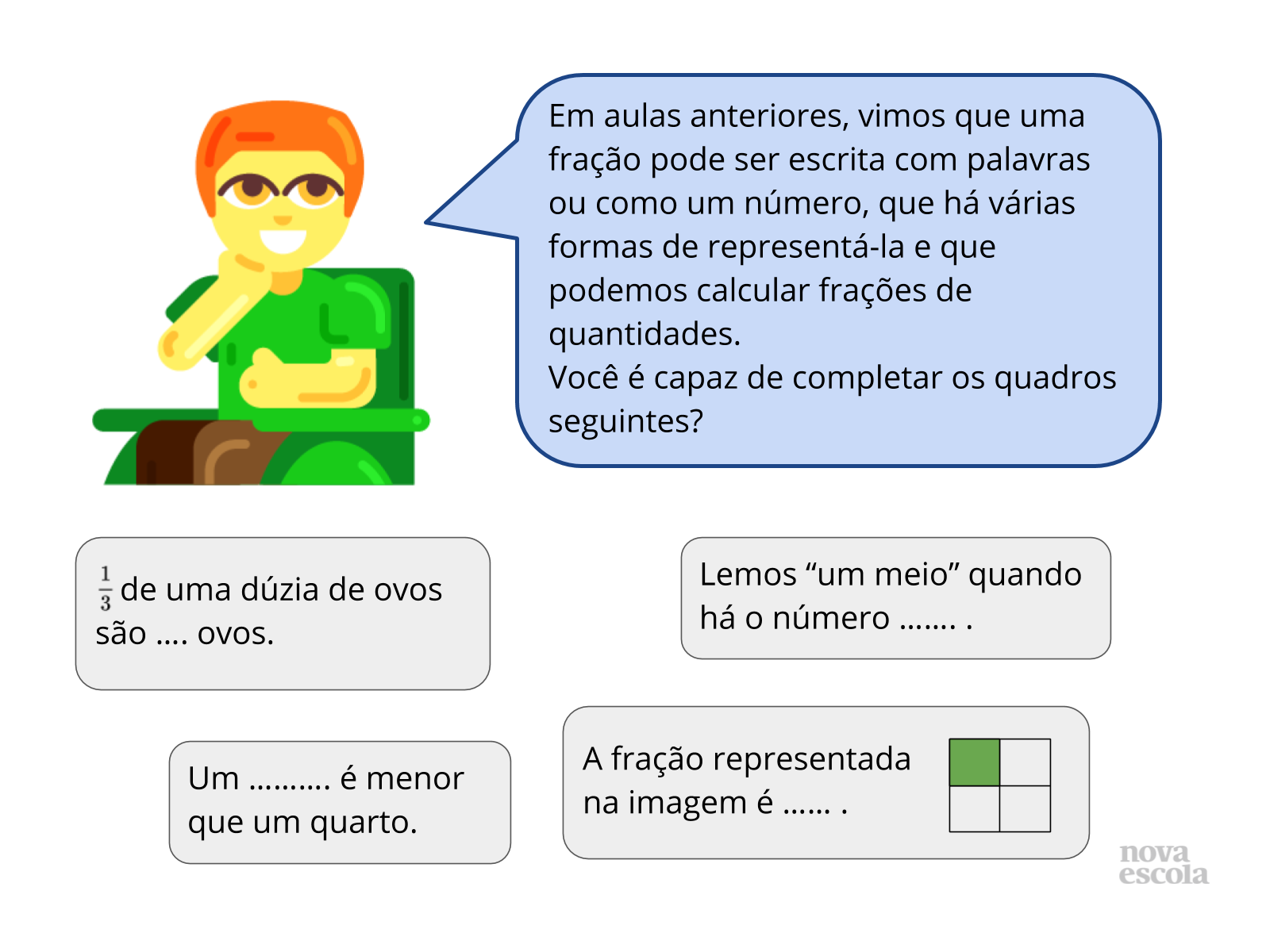
Tempo sugerido: 5 minutos.
Orientação: Organize os alunos em duplas. Projete o slide, entregue uma cópia ou copie-o no quadro. Leia o slide com os alunos e converse com eles sobre o que lembram acerca dos assuntos comentados no slide. Você pode orientar os alunos para que completem os quadrinhos nas duplas e depois socializem com a turma. É importante que todos compreendam as respostas dos quadrinhos. Note que no quadro que diz “Um ….. é menor que um quarto.”, há várias respostas possíveis, como ?, ? ou ?. Sempre deixe claro para os alunos que o número fracionário (½, ?, ¼, …) é um número, e não um número sobre outro. Em outras palavras, cada fração é um número, não dois sobrepostos. Portanto, não lemos “um sobre dois”, “um sobre três”, mas sim, “um meio”, “um terço”.
Propósito: Relembrar conceitos que serão importantes para a aula.
Discuta com a turma:
- Que outros números são menores que um quarto?
- Qual a fração que representa a parte não pintada do quadrado?
- Quanto é um quarto de uma dúzia de ovos? E um sexto?
- Que estratégia a dupla usou para completar as frases?
Possíveis respostas:
? de uma dúzia de ovos são 4 ovos.
Lemos “um meio” quando há o número ½.
Um quinto é menor que um quarto. (ou sexto, oitavo, décimo, …)
A fração representada na imagem é ¼.
Atividade Principal

Tempo sugerido: 24 minutos (Slides 4 e 5).
Orientação: Projete o slide, escreva-o no quadro ou entregue uma cópia da atividade para cada aluno. Leia a atividade com os alunos e oriente para que resolvam primeiro individualmente para, em seguida, compartilhar a resolução com o colega. Permita que os alunos desenhem o percurso em uma folha em branco ou pedaço em branco do seu caderno, usando sua criatividade. Se o aluno desenhar um percurso com curva, que não possa ser medido com a régua, questione como ele pode medir o percurso. Você pode entregar um pedaço de barbante para que o aluno meça onde fica cada fração. Caminhe pela sala e observe as formas que os alunos estão desenvolvendo a atividade. Anote as dúvidas para que sejam resolvidas no Painel de Soluções. Intervenha com perguntas quando necessário, auxiliando o aluno a resolver a atividade.
Propósito: Relembrar a representação de frações, frações na reta numerada e as frações de quantidade.
Discuta com a turma:
- O percurso precisa ser uma linha reta? Como posso medir um percurso que não é reto?
- Como você irá garantir que colocou cada animal no local correto do percurso?
- Qual animal foi o que andou mais? Quem ficou em segundo lugar? E quem andou menos?
- Você e seu colega de dupla representaram da mesma forma?
- Alguma dupla gostaria de mostrar aos colegas como desenhou o percurso?
- Materiais complementares:
Atividade Principal

Tempo sugerido: 24 minutos (Slides 4 e 5).
Orientação: Projete o slide, escreva-o no quadro ou entregue uma cópia da atividade para cada aluno. Leia a atividade com os alunos e oriente para que resolvam primeiro individualmente, para em seguida compartilhar a resolução com o colega. Na letra d, disponibilize materiais para que os alunos utilizem sua criatividade na representação das distâncias percorridas. Estimule para que os alunos demonstrem de forma diferente do que os colegas estão representando. Algumas sugestões: representando as frações com tiras ou discos de papel e comparando os pedaços (atentar apenas para que os discos/tiras inteiros tenham o mesmo tamanho), ou com barbante e pendurando um ao lado do outro, para comparar. Caminhe pela sala e observe as formas que os alunos estão desenvolvendo a atividade. Anote as dúvidas para que sejam resolvidas no Painel de Soluções. Intervenha com perguntas quando necessário, auxiliando o aluno a resolver a atividade.
Propósito: Relembrar a representação de frações, frações na reta numerada e as frações de quantidade.
Discuta com a turma:
- Observe a diferença da distância percorrida pela tartaruga se a pista medisse 120 ou 240 metros. Agora observe a diferença da distância percorrida pelo cachorro. Para qual deles a diferença é maior? Por quê?
- O que mais você observa sobre as distâncias percorridas nas pistas diferentes?
- Como você pensou em representar as frações?
- Quem representou de outras formas?
- Há alguma outra forma possível que ninguém da turma utilizou?
Painel de Soluções

Tempo sugerido: 10 minutos (Slides 6, 7, 8 e 9).
Orientação: Finalizando a atividade principal, passe para essa etapa. Antes de trabalhar com os slides, você pode conversar com os alunos sobre como resolveram a atividade, tendo como base as observações que fez enquanto resolviam. Peça que alunos que resolveram de formas diferentes mostrem aos colegas que caminho seguiram para encontrar a solução. Entregue uma cópia do slide para os alunos, projete ou copie no quadro. Leia com a turma e faça perguntas de forma que os alunos solucionem suas dúvidas, ajudando uns aos outros. Certifique-se que todos os alunos compreenderam pelo menos uma forma de resolução da atividade.
Propósito: Socializar as respostas dos alunos e verificar se estão corretas.
Discuta com a turma:
- Suas anotações estão semelhantes às anotações de seus colegas?
- Todos responderam da mesma forma?
- Quem o fez de forma diferente, pode explicar como fez?
Painel de Soluções

Tempo sugerido: 10 minutos (Slides 6, 7, 8 e 9).
Orientação: Finalizando a atividade principal, passe para essa etapa. Antes de trabalhar com os slides, você pode conversar com os alunos sobre como resolveram a atividade, tendo como base as observações que fez enquanto resolviam. Peça que alunos que resolveram de formas diferentes mostrem aos colegas que caminho seguiram para encontrar a solução. Entregue uma cópia do slide para os alunos, projete ou copie no quadro. Leia com a turma e faça perguntas de forma que os alunos solucionem suas dúvidas, ajudando uns aos outros. Como atividade complementar, você pode pedir que os alunos calculem as distâncias percorridas se o percurso tivesse outros comprimentos, como 250 ou 300 metros, de forma que os cálculos das distâncias não deem números inteiros. Certifique-se que todos os alunos compreenderam pelo menos uma forma de resolução da atividade.
Propósito: Socializar as respostas dos alunos e verificar se estão corretas.
Discuta com a turma:
- Suas anotações estão iguais às expostas nos slides?
- Todos percorreram o mesmo caminho para chegar a resposta?
- Quem calculou de outra forma, pode explicar para a turma como fez?
- Todos chegaram à mesma resposta?
- Quem respondeu de forma diferente, pode explicar como fez?
Painel de Soluções

Tempo sugerido: 10 minutos (Slides 6, 7, 8 e 9).
Orientação: Finalizando a atividade principal, passe para essa etapa. Antes de trabalhar com os slides, você pode conversar com os alunos sobre como resolveram a atividade, tendo como base as observações que fez enquanto resolviam. Peça que alunos que resolveram de formas diferentes mostrem aos colegas que caminho seguiram para encontrar a solução. Entregue uma cópia do slide para os alunos, projete ou copie no quadro. Leia com a turma e faça perguntas de forma que os alunos solucionem suas dúvidas, ajudando uns aos outros. Como atividade complementar, você pode pedir que os alunos calculem as distâncias percorridas se o percurso tivesse outros comprimentos, como 250 ou 300 metros, de forma que os cálculos das distâncias não deem números inteiros. Certifique-se que todos os alunos compreenderam pelo menos uma forma de resolução da atividade.
Propósito: Socializar as respostas dos alunos e verificar se estão corretas.
Discuta com a turma:
- Suas anotações estão iguais às expostas nos slides?
- Todos percorreram o mesmo caminho para chegar a resposta?
- Quem calculou de outra forma, pode explicar para a turma como fez?
- Todos chegaram à mesma resposta?
- Quem respondeu de forma diferente, pode explicar como fez?
Painel de Soluções
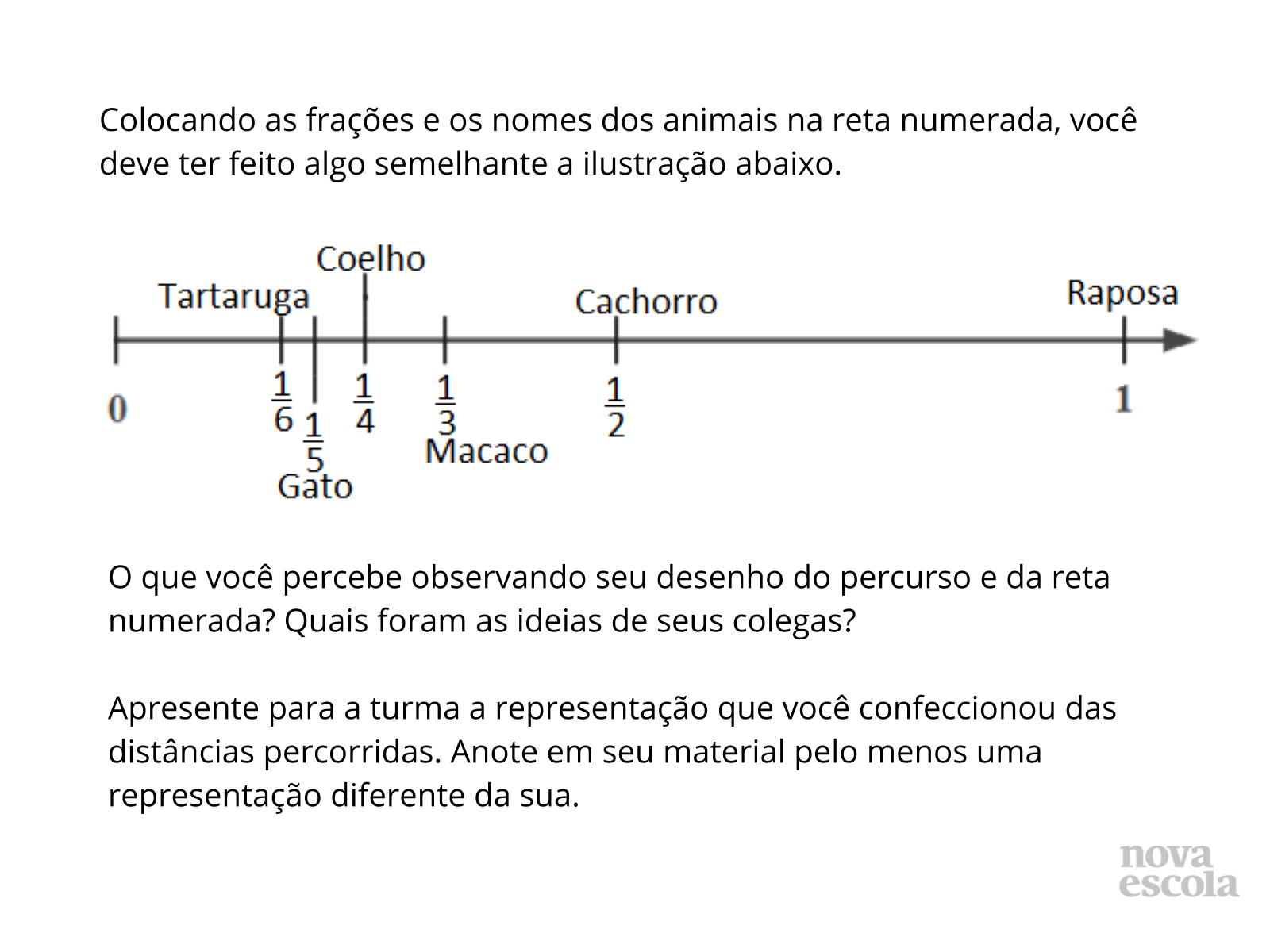
Tempo sugerido: 10 minutos (Slides 6, 7, 8 e 9).
Orientação: Finalizando a atividade principal, passe para essa etapa. Antes de trabalhar com os slides, você pode conversar com os alunos sobre como resolveram a atividade, tendo como base as observações que fez enquanto resolviam. Peça que alunos que resolveram de formas diferentes mostrem aos colegas que caminho seguiram para encontrar a solução. Entregue uma cópia do slide para os alunos, projete ou copie no quadro. Leia com a turma e faça perguntas de forma que os alunos solucionem suas dúvidas, ajudando uns aos outros. Espera-se que os alunos percebam que a ordem dos animais na reta numerada e no percurso é a mesma, e que as distâncias entre os animais são proporcionais. Estimule para que os alunos falem sobre a sua representação aos colegas e que façam perguntas caso algo não fique claro. Anotando uma ideia de representação diferente da que fizeram, os alunos demonstram que assimilaram a ideia do colega. Certifique-se que todos os alunos compreenderam pelo menos uma forma de resolução da atividade.
Propósito: Socializar as respostas dos alunos e verificar se estão corretas.
Discuta com a turma:
- Suas anotações estão iguais às expostas nos slides?
- Todos percorreram o mesmo caminho para chegar a resposta?
- Quem calculou de outra forma, pode explicar para a turma como fez?
- Todos chegaram à mesma resposta?
- Quem respondeu de forma diferente, pode explicar como fez?
- Você compreendeu a maneira que o seu colega representou as frações?
- Há alguma representação possível diferente das feitas pela turma?
Encerramento
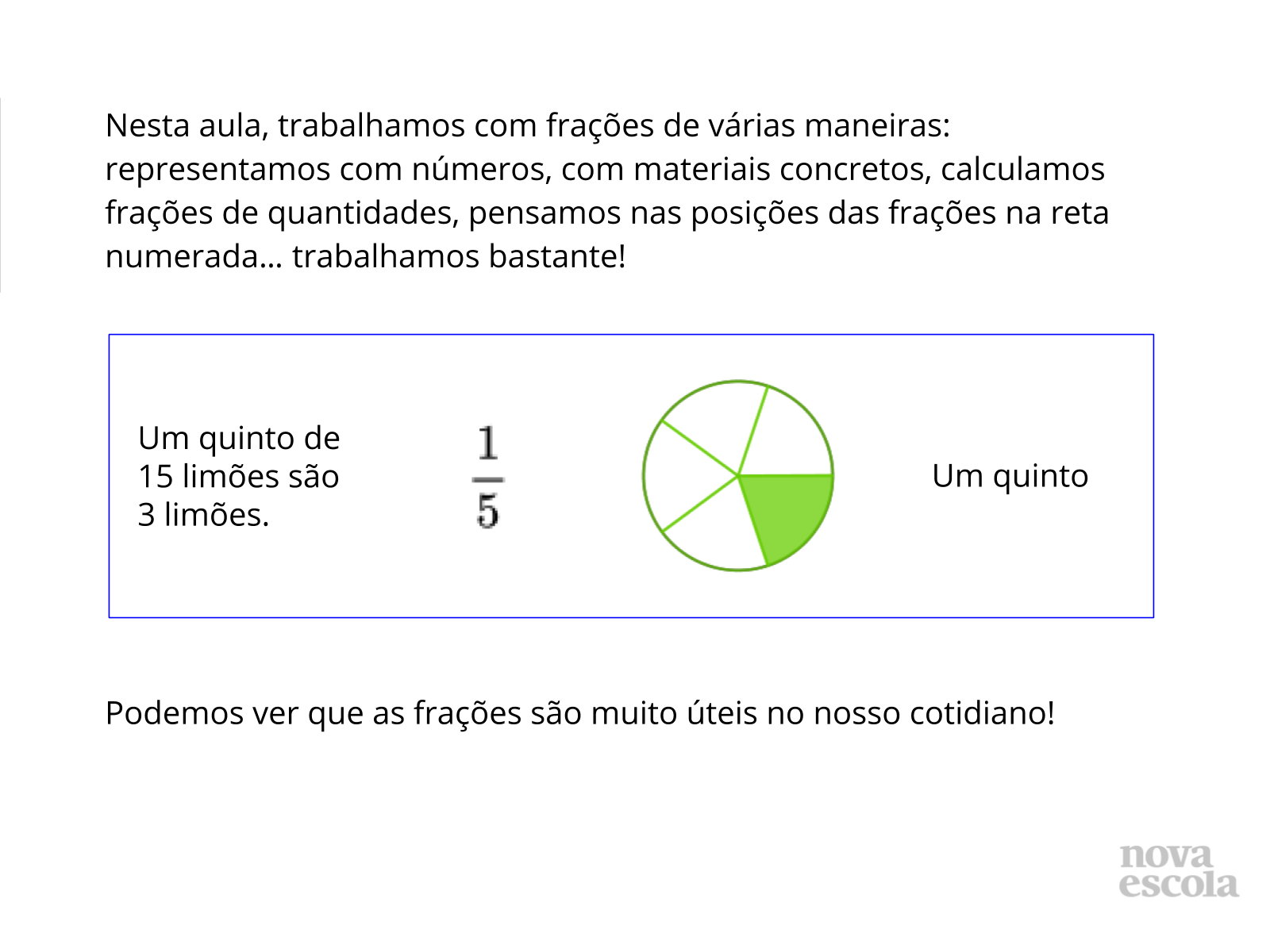
Tempo sugerido: 5 minutos
Orientação: Converse com os alunos sobre a aula. Projete o slide para os alunos, entregue uma cópia ou copie-o no quadro. Leia o slide com os alunos. Você pode pedir que os alunos anotem em seu caderno um breve resumo do que foi visto na aula.
Propósito: Resumir o que foi visto na aula.
Discuta com a turma:
- Como você e seu grupo abordaram o problema da aula de hoje?
- Seus erros foram corrigidos? Ficou alguma dúvida?
- O que mais gostaram na aula de hoje?
- Aprenderam algo que não conheciam?
Raio X

Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa. Em seguida, você pode propor aos alunos as atividades complementares, que podem ser realizadas na sala ou como tarefa de casa.
Propósito: Testar se os alunos compreenderam o que foi visto na aula.
Discuta com a turma:
- Quantos balões do total foram utilizados para o palco? Que fração essa quantidade representa?
- Se metade dos balões do arco eram amarelos, quantos balões amarelos havia no arco?
- Há apenas uma forma de chegar à resposta?
- Quem chegou a uma resposta diferente, pode explicar para a turma como fez?
Materiais complementares:
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_11NUM_07
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: -
- Opcionais: Jamboard, Google Formulários, Google Documentos.
Para este plano, foque na etapa Atividade Principal.
Retomada
O professor pode transpor a atividade para o Google Formulários, incluindo as questões das orientações ao professor para que os alunos respondam também.
No caso da turma não usar a internet, o professor pode fazer o mesmo movimento com atividade impressa.
Atividade principal
Organizar a atividade para ser respondida com o auxílio do Jamboard ou, caso a turma não tenha acesso ao recurso, pode ser feito em registro escrito.
Discussão das soluções
O professor pode solicitar que os alunos usem uma tira de papel para representar a pista e identificarem a posição dos animais após o percurso de cada um. As tiras de papel podem ser enviadas ao professor ou fotografadas para envio da imagem, além das respostas às questões propostas para discussão (sendo respondidas individualmente).
Sistematização
Não há.
Encerramento
Propor que os alunos partilhem suas aprendizagens com os demais integrantes da turma usando o Google Documentos, em que cada um faz um breve relato e indica o nome. Caso o recurso não esteja disponível para a turma, o professor pode solicitar que eles enviem esse relato em papel para ser organizado e socializado pelo próprio professor.
Raio X
Propor que os alunos respondam à atividade indicada, apontando o que eles consideraram mais fácil e mais difícil de descobrir.
Convite às famílias
Propor que a família crie com o aluno um problema similar ao apresentado no Raio X e coloque na problemoteca do aluno (caso ele ainda não possua uma problemoteca, eis o momento de criá-la! O professor pode sugerir a inserção dos outros problemas discutidos no plano de aula nessa problemoteca).
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Thaís Schulz
Mentor: Elisa Greenhalgh Vilalta
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA09 - Reconhecer as frações unitárias mais usuais (1/2, 1/3, 1/4, 1/5, 1/10 e 1/100) como unidades de medida menores do que uma unidade, utilizando a reta numérica como recurso.
Objetivos específicos
Calcular frações de quantidade, envolvendo meios, terços, quartos, quintos e sextos.
Conceito-chave
Cálculo de frações
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Materiais para a representação das frações (barbante, papel colorido, isopor, discos de pizza, marcadores, giz e lápis coloridos, etc.);
- Réguas (suficientes para a turma);
- Barbante ou lã.















