Atividade principal
Plano de Aula
Plano de aula: Relações inversas entre multiplicação e divisão com resto zero
Plano 3 de uma sequência de 5 planos. Veja todos os planos sobre Investigação de padrões em operações fundamentais
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Márcia Regina Kaminski
Mentora: Carla Simone Albuquerque
Revisora Pedagógica: Eliane Zanin
Especialista de área: Sandra Regina Correa Amorim
Habilidade da BNCC
(EF04MA13) Reconhecer, por meio de investigações, utilizando a calculadora quando necessário, as relações inversas entre as operações de adição e de subtração e de multiplicação e de divisão, para aplicá-las na resolução de problemas.
Objetivos específicos
- Trabalhar as relações inversas entre multiplicação e divisão a partir de situações problemas.
- Compreender que as operações de multiplicação e divisão são inversas e que envolvem um significado.
Conceito-chave
- Investigação de padrões em operações: entre multiplicação e divisão com resto zero com os números naturais.
Vocabulário
- Multiplicação.
- Divisão.
- Inversa.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
- Lápis preto e de cor,
- Datashow ( opcional ).
Habilidades BNCC:
Objetivos de aprendizagem
- Trabalhar as relações inversas entre multiplicação e divisão a partir de situações problemas.
- Compreender que as operações de multiplicação e divisão são inversas e que envolvem um significado.
Resumo da aula
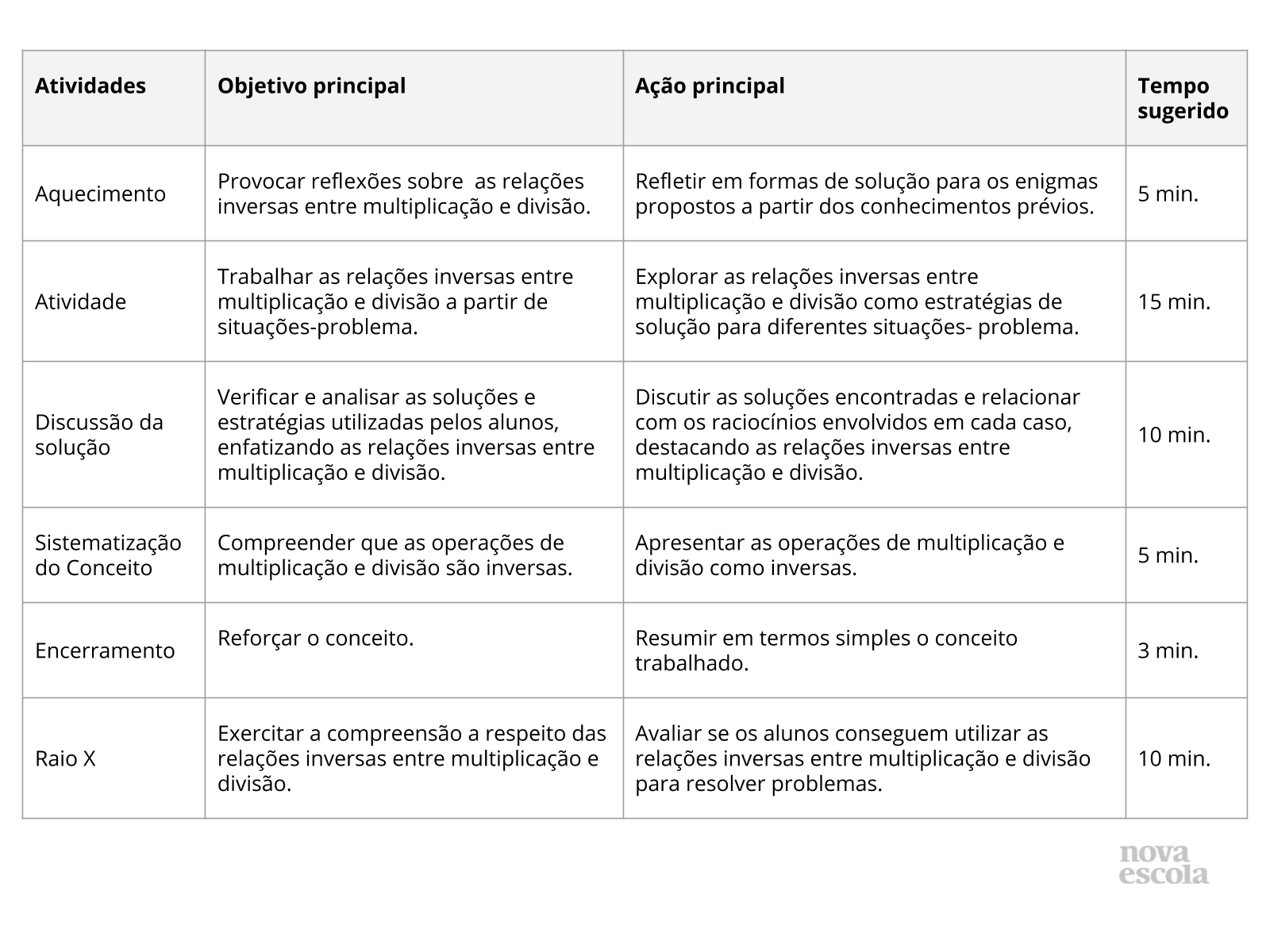
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 5 minutos.
Orientação: Leia o conteúdo do slide com a turma e questione: É possível identificar qual é o número que está faltando em cada uma das operações? Reserve 3 minutos para que os alunos pensem e tentem resolver. Depois questione oral e coletivamente quais as estratégias que eles elaboraram para responder. Peça que alguns alunos apresentem a forma como pensaram para os colegas, e discuta com a turma. No primeiro caso, os alunos devem perceber que se 8 vezes algum número resulta em 32, então 32 dividido por 8 nos indica qual é esse número. Neste caso, como 32 dividido por 8 é 4, o número oculto é 4. Seguindo a mesma ideia, no segundo caso, um número vezes 5 é igual a 45. Então, 45 dividido por 5 é igual a este número. Como 45 dividido por 5 é igual a 9, então 9 é o número oculto. No terceiro caso, algum número dividido por 3 é igual a 7. Então podemos pensar que em uma divisão foram formados 3 grupos com 7 elementos. Isso significa que 3 x 7 é igual à quantidade que foi dividida. Neste caso 3 x 7 = 21. Portanto 21 é o número oculto. Alguns alunos podem pensar diretamente na tabuada para responder os enigmas. Deixe que eles comentem como pensaram.
Propósito: Introduzir as relações inversas entre as operações de multiplicação e divisão com resto zero.
Discuta com a turma:
- Será que é possível identificar os números ocultos?
- Como vocês fariam?
- Por onde podemos começar a pensar na solução?
Atividade principal

Tempo sugerido: 15 minutos.
Orientação: Leia as questões com os alunos e proponha que respondam, trabalhando em duplas. Permita que eles utilizem diferentes estratégias para encontrar a solução. Acompanhe o trabalho das duplas, observando os caminhos utilizados por eles para resolver e auxiliando através de questionamentos sempre que necessário.
Propósito: Explorar as relações inversas entre multiplicação e divisão com resto zero como diferentes possibilidades de solução para um problema.
Discuta com a turma:
- Como podemos pensar para responder cada uma das questões?
- Por que vocês escolheram esta forma de solução?
- É possível resolver de outra maneira?
Materiais complementares:
Discussão de soluções
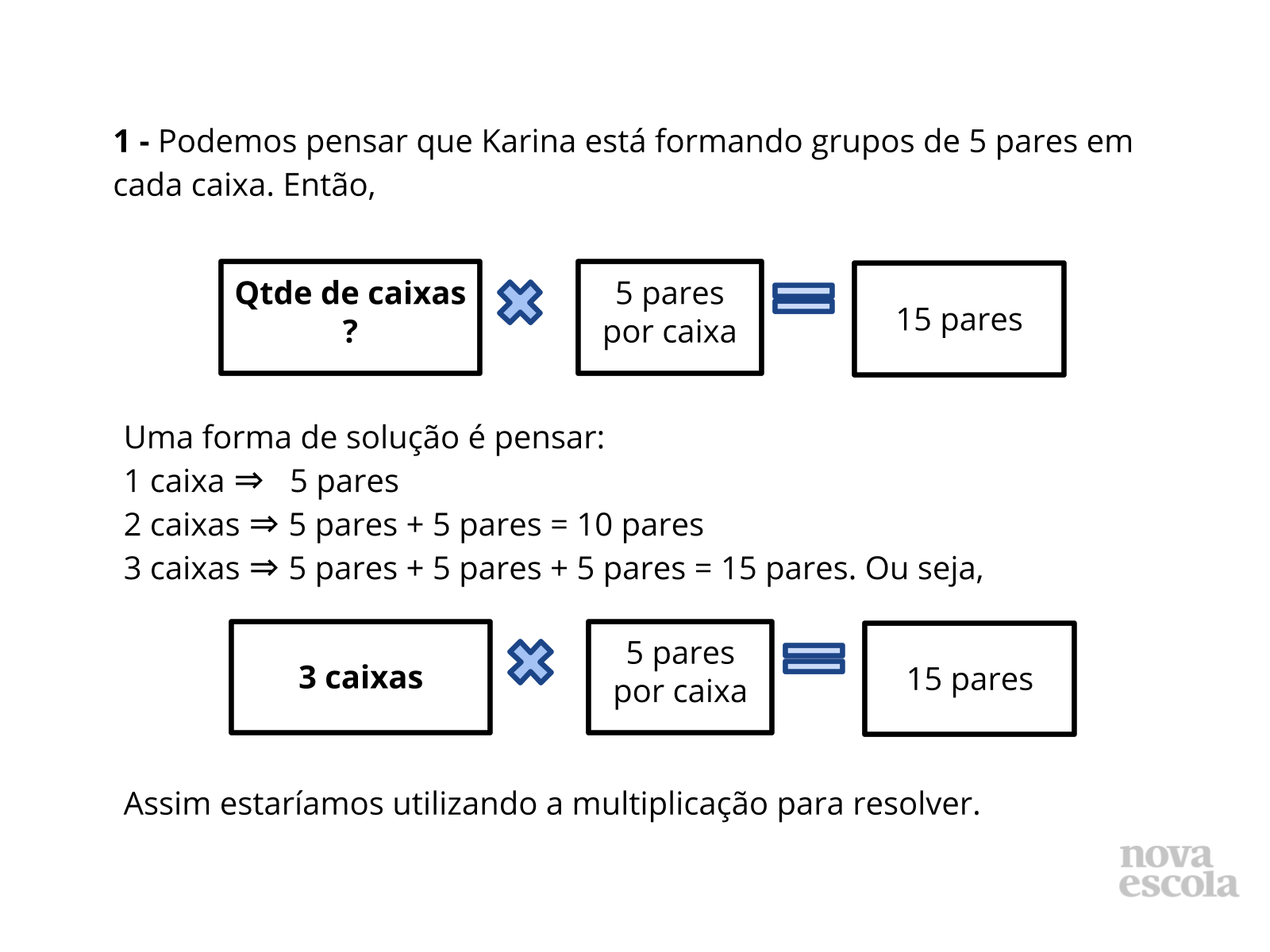
Tempo sugerido: 10 minutos. (Slides 5 a 14)
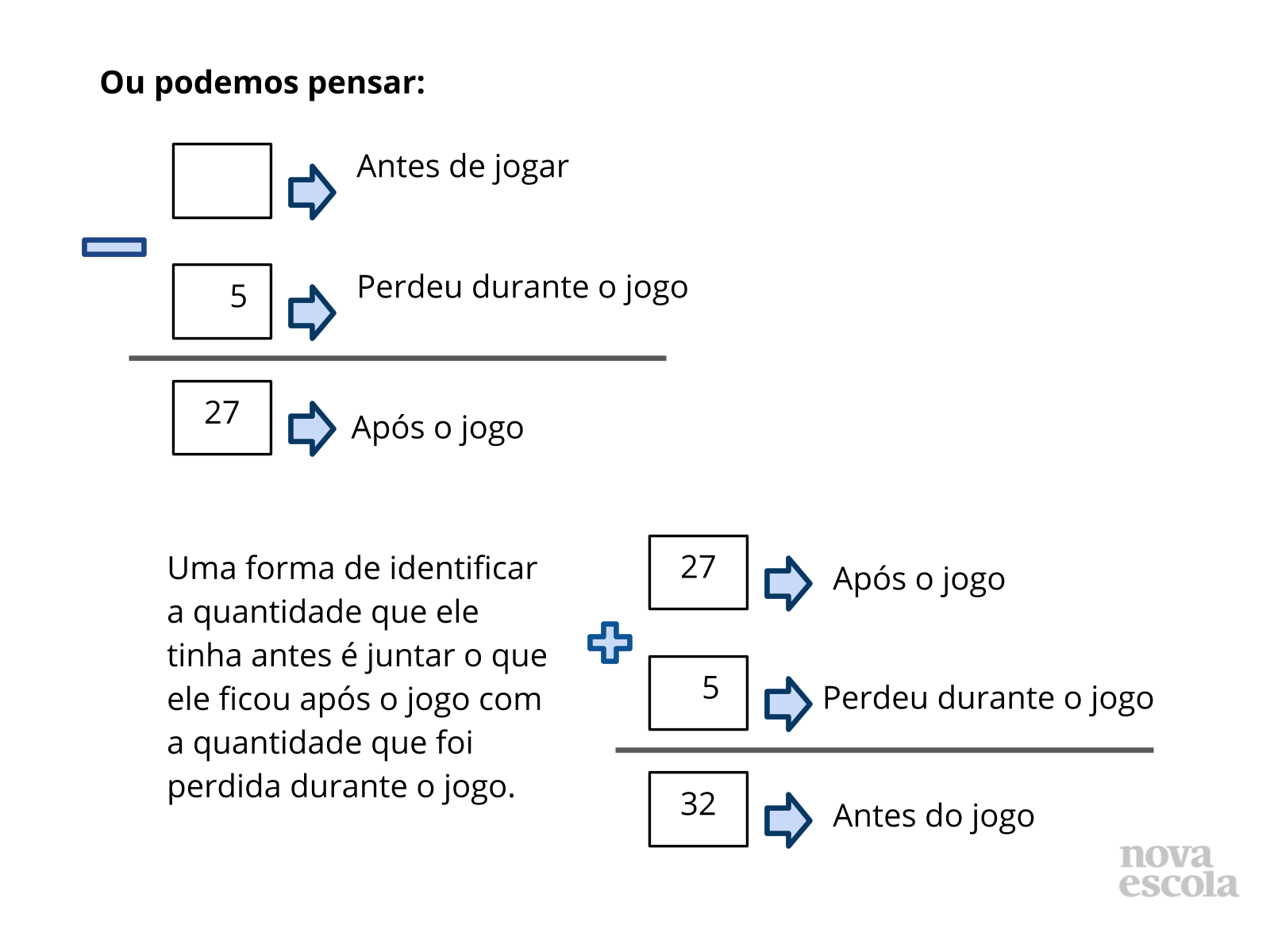
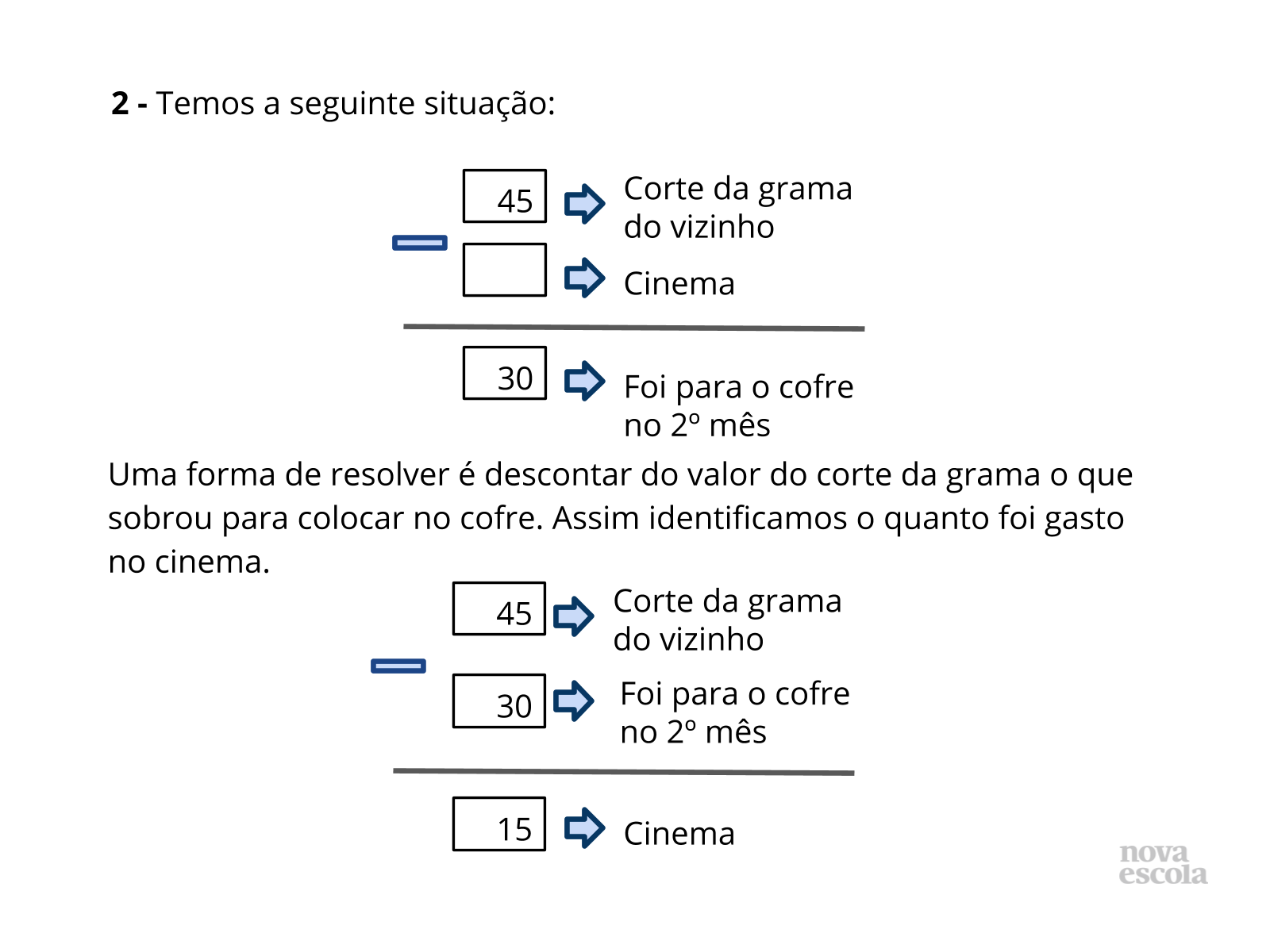
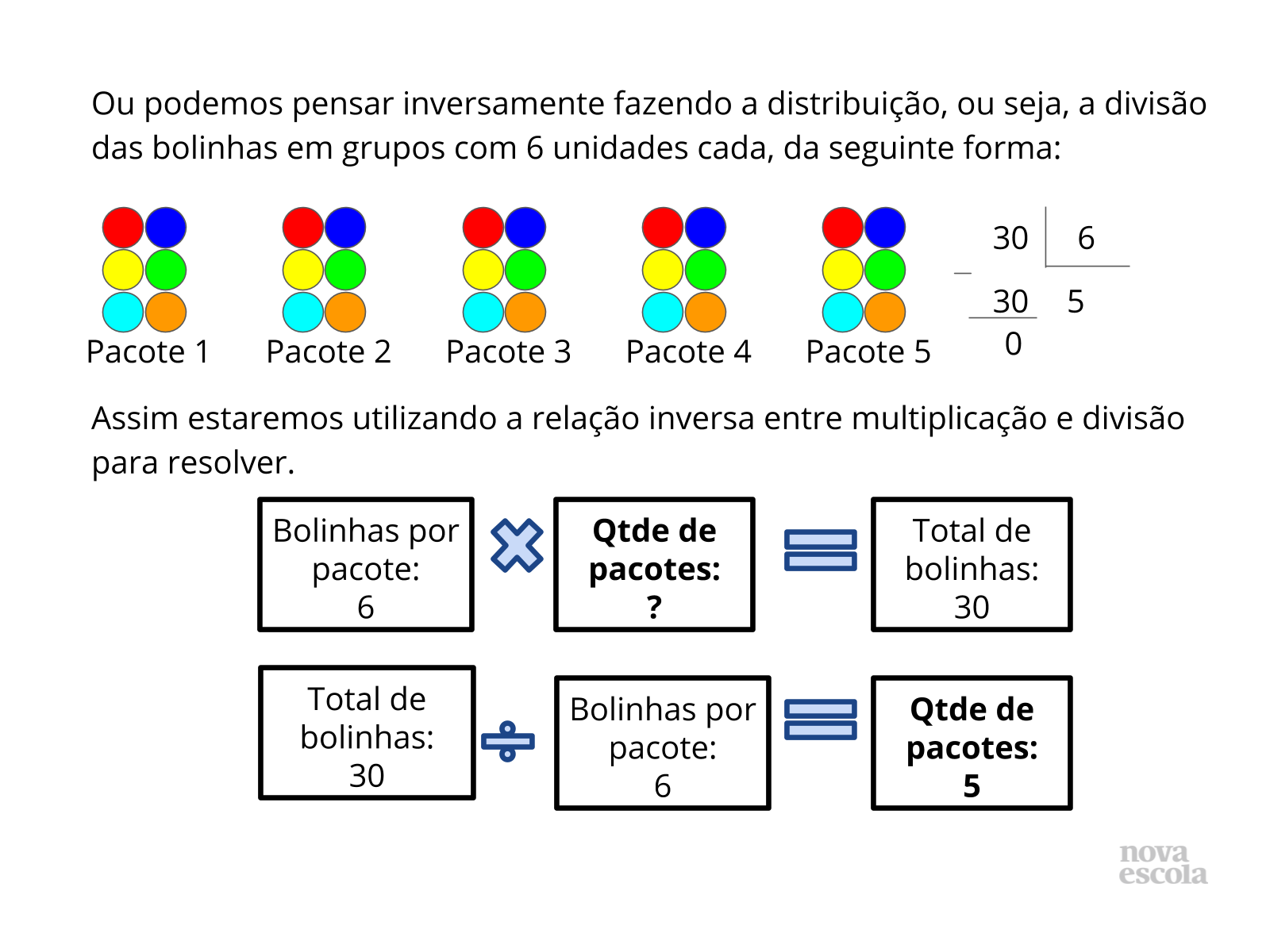
Orientação: Questione as duplas sobre as estratégias que utilizaram para resolver. Depois apresente as sugestões de solução dos slides. Destaque que para cada questão é possível pensar de diferentes formas, e elaborar diferentes estratégias para encontrar a resposta. É possível pensar por meio de uma multiplicação, ou de uma divisão. Isso é possível devido às relações inversas entre multiplicação e divisão. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Caso haja alguma solução equivocada, utilize esse momento para discutir com a turma onde ocorreu o equívoco.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos e apresentar as relações inversas entre multiplicação e divisão com resto zero.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Há mais de uma forma de resolver?
- Como podemos ter certeza de que está correto?
- Será que é possível resolver utilizando operações diferentes?
Material Complementar:
Discussão de soluções
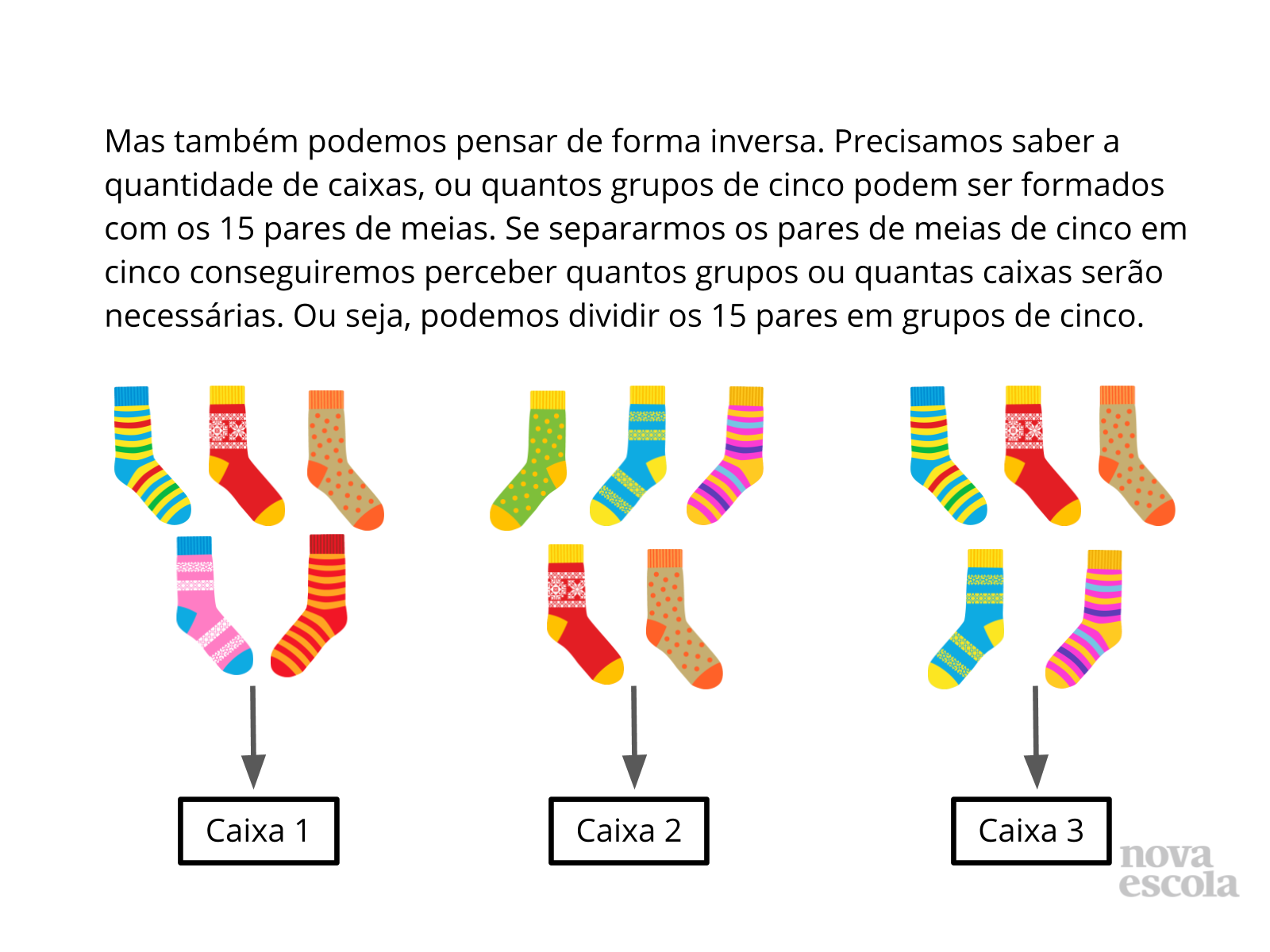
Tempo sugerido: 10 minutos. (Slides 5 a 14)
Orientação: Questione as duplas sobre as estratégias que utilizaram para resolver. Depois apresente as sugestões de solução dos slides. Destaque que para cada questão é possível pensar de diferentes formas, e elaborar diferentes estratégias para encontrar a resposta. É possível pensar por meio de uma multiplicação, ou de uma divisão. Isso é possível devido às relações inversas entre multiplicação e divisão. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Caso haja alguma solução equivocada, utilize esse momento para discutir com a turma onde ocorreu o equívoco.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos e apresentar as relações inversas entre multiplicação e divisão com resto zero.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Há mais de uma forma de resolver?
- Como podemos ter certeza de que está correto?
- Será que é possível resolver utilizando operações diferentes?
Discussão de soluções
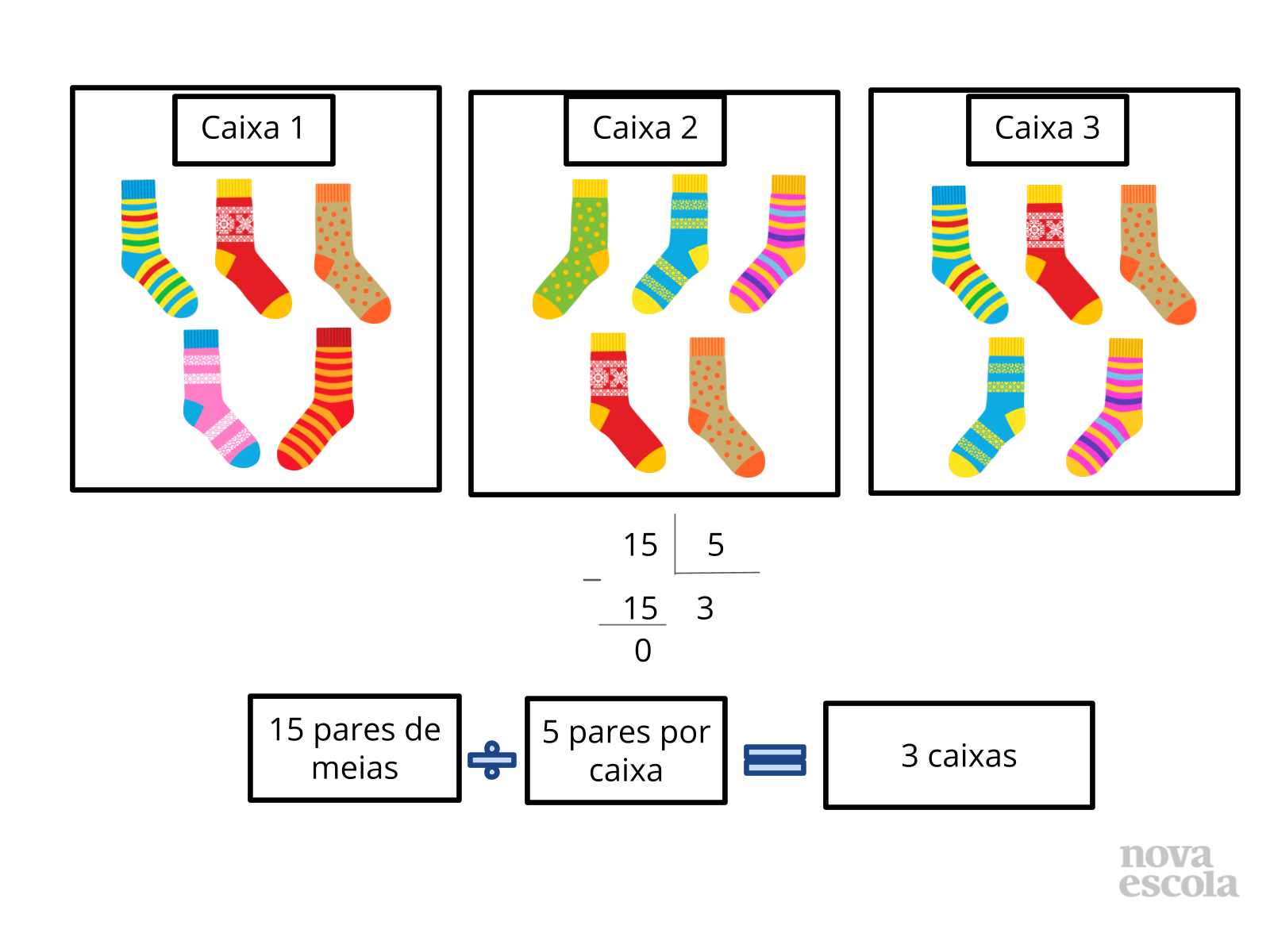
Tempo sugerido: 10 minutos. (Slides 5 a 14)
Orientação: Questione as duplas sobre as estratégias que utilizaram para resolver. Depois apresente as sugestões de solução dos slides. Destaque que para cada questão é possível pensar de diferentes formas, e elaborar diferentes estratégias para encontrar a resposta. É possível pensar por meio de uma multiplicação, ou de uma divisão. Isso é possível devido às relações inversas entre multiplicação e divisão. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Caso haja alguma solução equivocada, utilize esse momento para discutir com a turma onde ocorreu o equívoco.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos e apresentar as relações inversas entre multiplicação e divisão com resto zero.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Há mais de uma forma de resolver?
- Como podemos ter certeza de que está correto?
- Será que é possível resolver utilizando operações diferentes?
Discussão de soluções
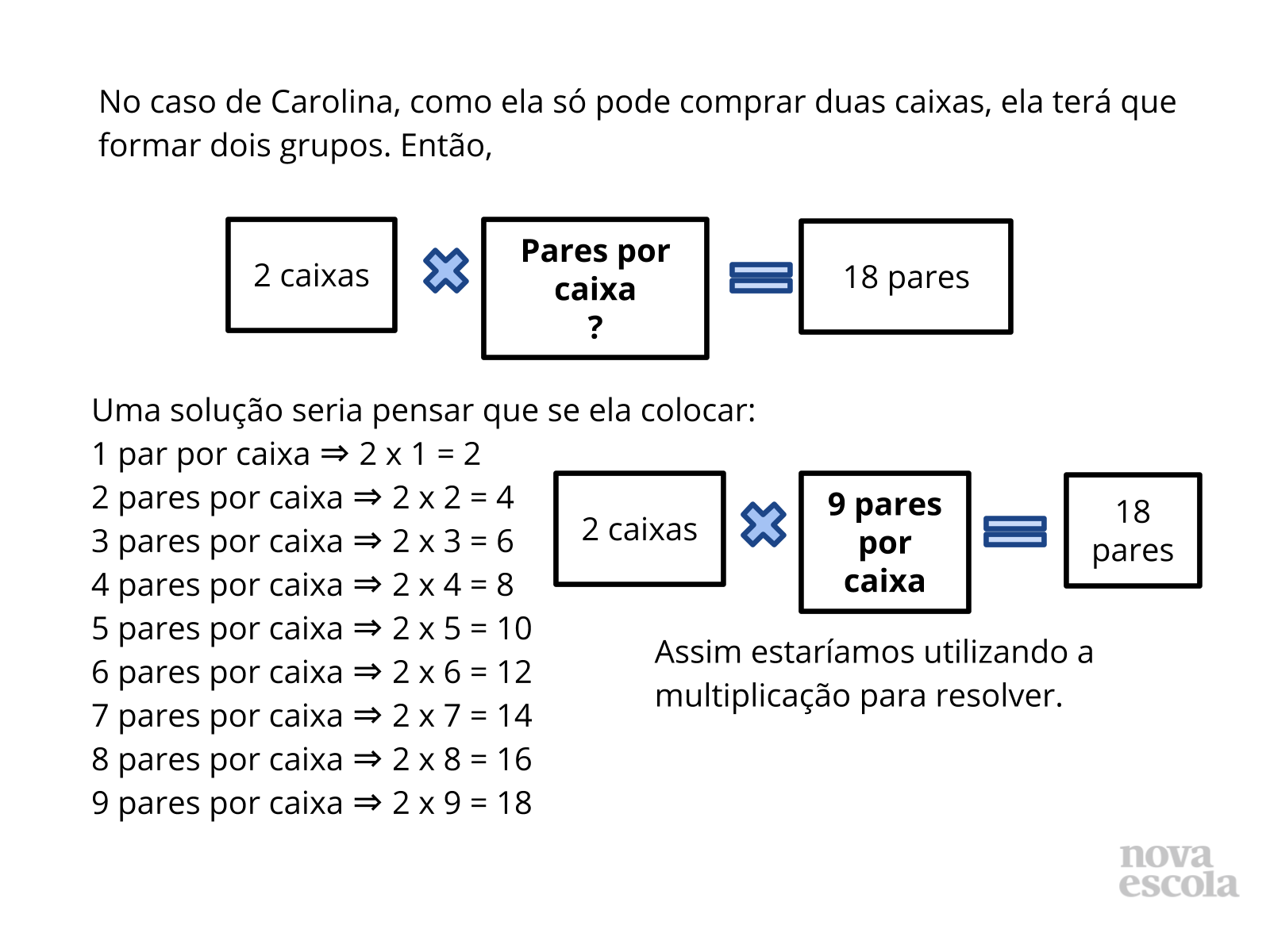
Tempo sugerido: 10 minutos. (Slides 5 a 14)
Orientação: Questione as duplas sobre as estratégias que utilizaram para resolver. Depois apresente as sugestões de solução dos slides. Destaque que para cada questão é possível pensar de diferentes formas, e elaborar diferentes estratégias para encontrar a resposta. É possível pensar por meio de uma multiplicação, ou de uma divisão. Isso é possível devido às relações inversas entre multiplicação e divisão. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Caso haja alguma solução equivocada, utilize esse momento para discutir com a turma onde ocorreu o equívoco.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos e apresentar as relações inversas entre multiplicação e divisão com resto zero.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Há mais de uma forma de resolver?
- Como podemos ter certeza de que está correto?
- Será que é possível resolver utilizando operações diferentes?
Discussão de soluções
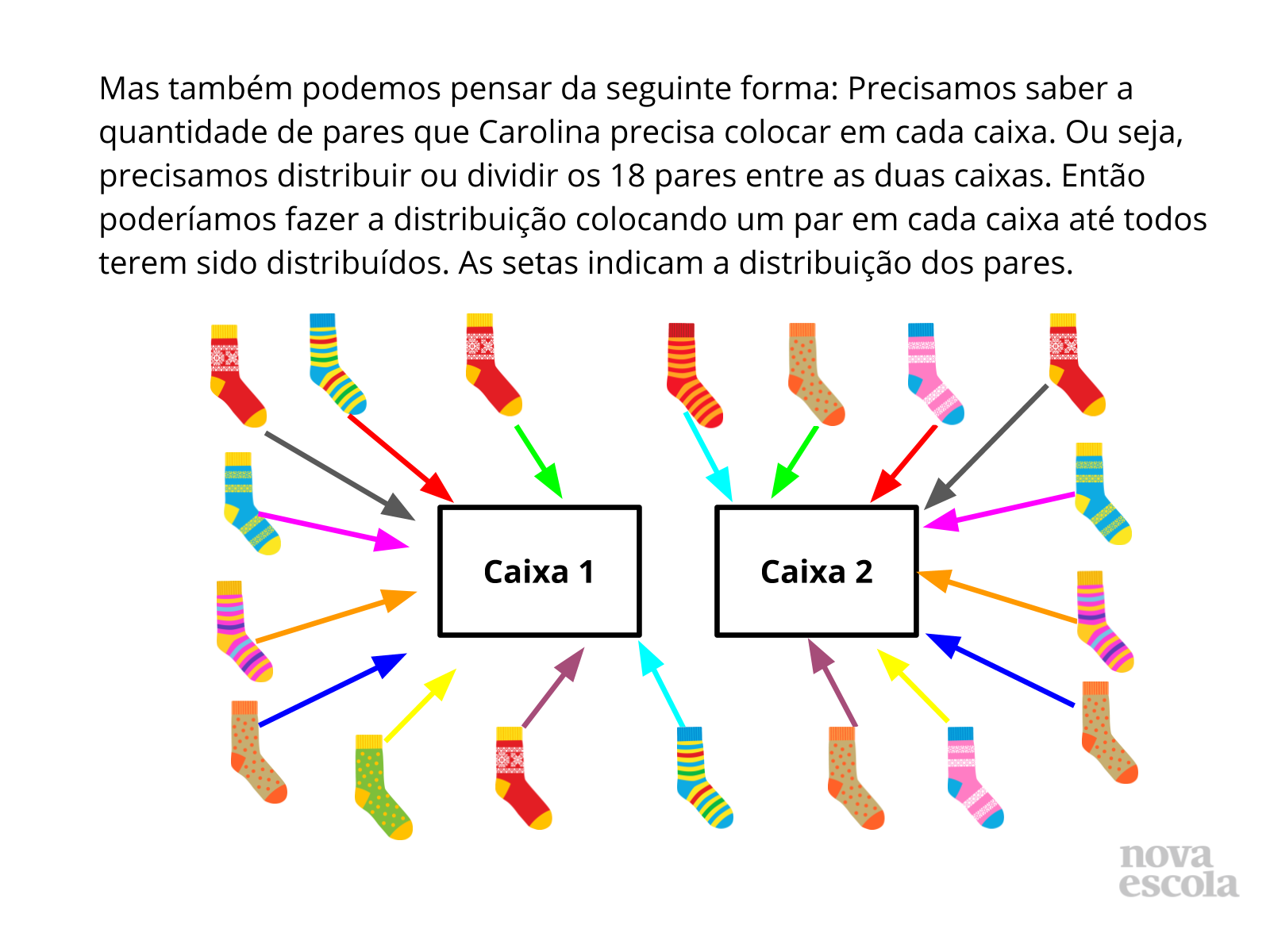
Tempo sugerido: 10 minutos. (Slides 5 a 14)
Orientação: Questione as duplas sobre as estratégias que utilizaram para resolver. Depois apresente as sugestões de solução dos slides. Destaque que para cada questão é possível pensar de diferentes formas, e elaborar diferentes estratégias para encontrar a resposta. É possível pensar por meio de uma multiplicação, ou de uma divisão. Isso é possível devido às relações inversas entre multiplicação e divisão. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Caso haja alguma solução equivocada, utilize esse momento para discutir com a turma onde ocorreu o equívoco.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos e apresentar as relações inversas entre multiplicação e divisão com resto zero.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Há mais de uma forma de resolver?
- Como podemos ter certeza de que está correto?
- Será que é possível resolver utilizando operações diferentes?
Discussão de soluções
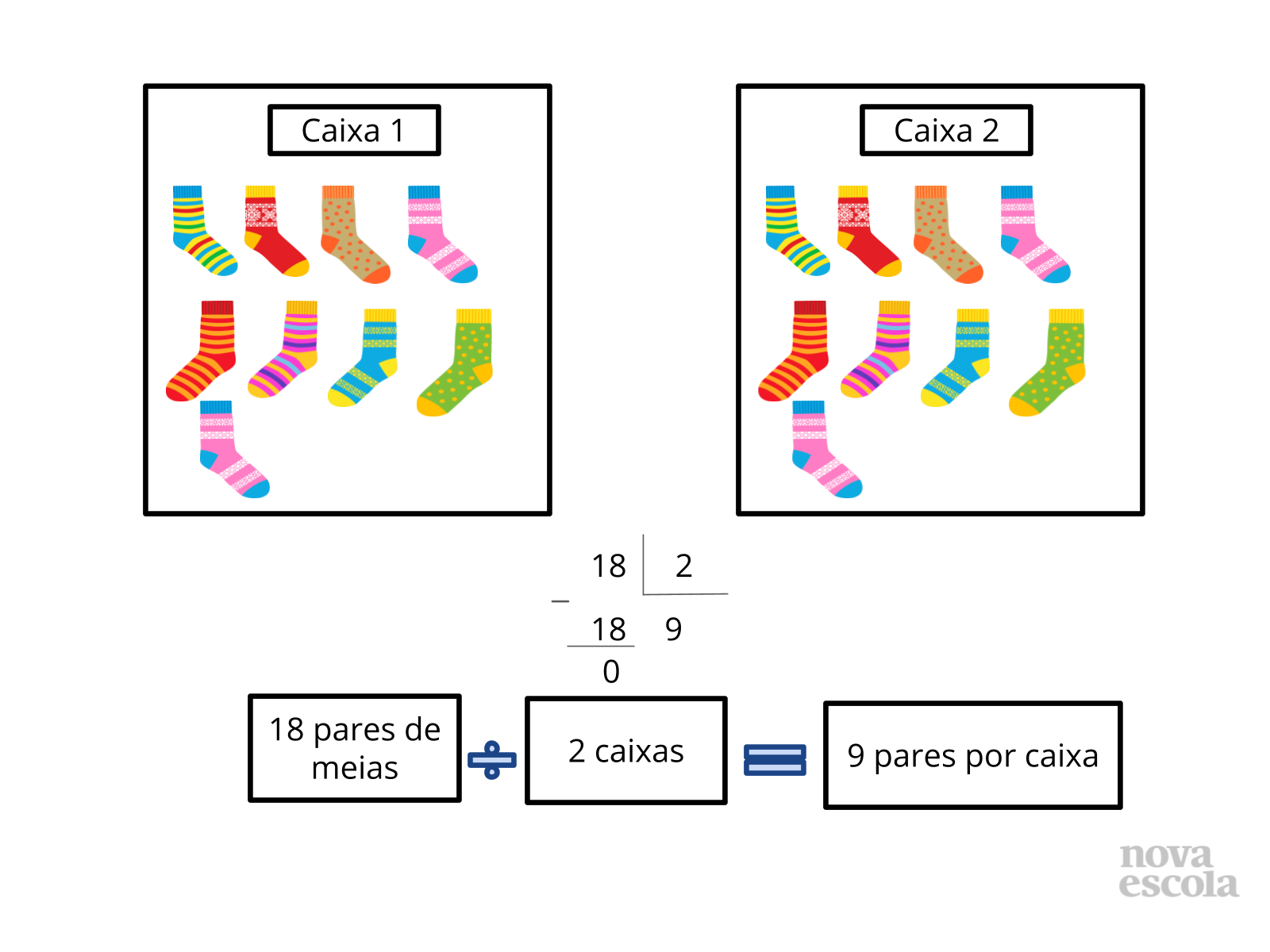
Tempo sugerido: 10 minutos. (Slides 5 a 14)
Orientação: Questione as duplas sobre as estratégias que utilizaram para resolver. Depois apresente as sugestões de solução dos slides. Destaque que para cada questão é possível pensar de diferentes formas, e elaborar diferentes estratégias para encontrar a resposta. É possível pensar por meio de uma multiplicação, ou de uma divisão. Isso é possível devido às relações inversas entre multiplicação e divisão. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Caso haja alguma solução equivocada, utilize esse momento para discutir com a turma onde ocorreu o equívoco.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos e apresentar as relações inversas entre multiplicação e divisão com resto zero.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Há mais de uma forma de resolver?
- Como podemos ter certeza de que está correto?
- Será que é possível resolver utilizando operações diferentes?
Discussão de soluções

Tempo sugerido: 10 minutos. (Slides 5 a 14)
Orientação: Questione as duplas sobre as estratégias que utilizaram para resolver. Depois apresente as sugestões de solução dos slides. Destaque que para cada questão é possível pensar de diferentes formas, e elaborar diferentes estratégias para encontrar a resposta. É possível pensar por meio de uma multiplicação, ou de uma divisão. Isso é possível devido às relações inversas entre multiplicação e divisão. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Caso haja alguma solução equivocada, utilize esse momento para discutir com a turma onde ocorreu o equívoco.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos e apresentar as relações inversas entre multiplicação e divisão com resto zero.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Há mais de uma forma de resolver?
- Como podemos ter certeza de que está correto?
- Será que é possível resolver utilizando operações diferentes?
Discussão de soluções
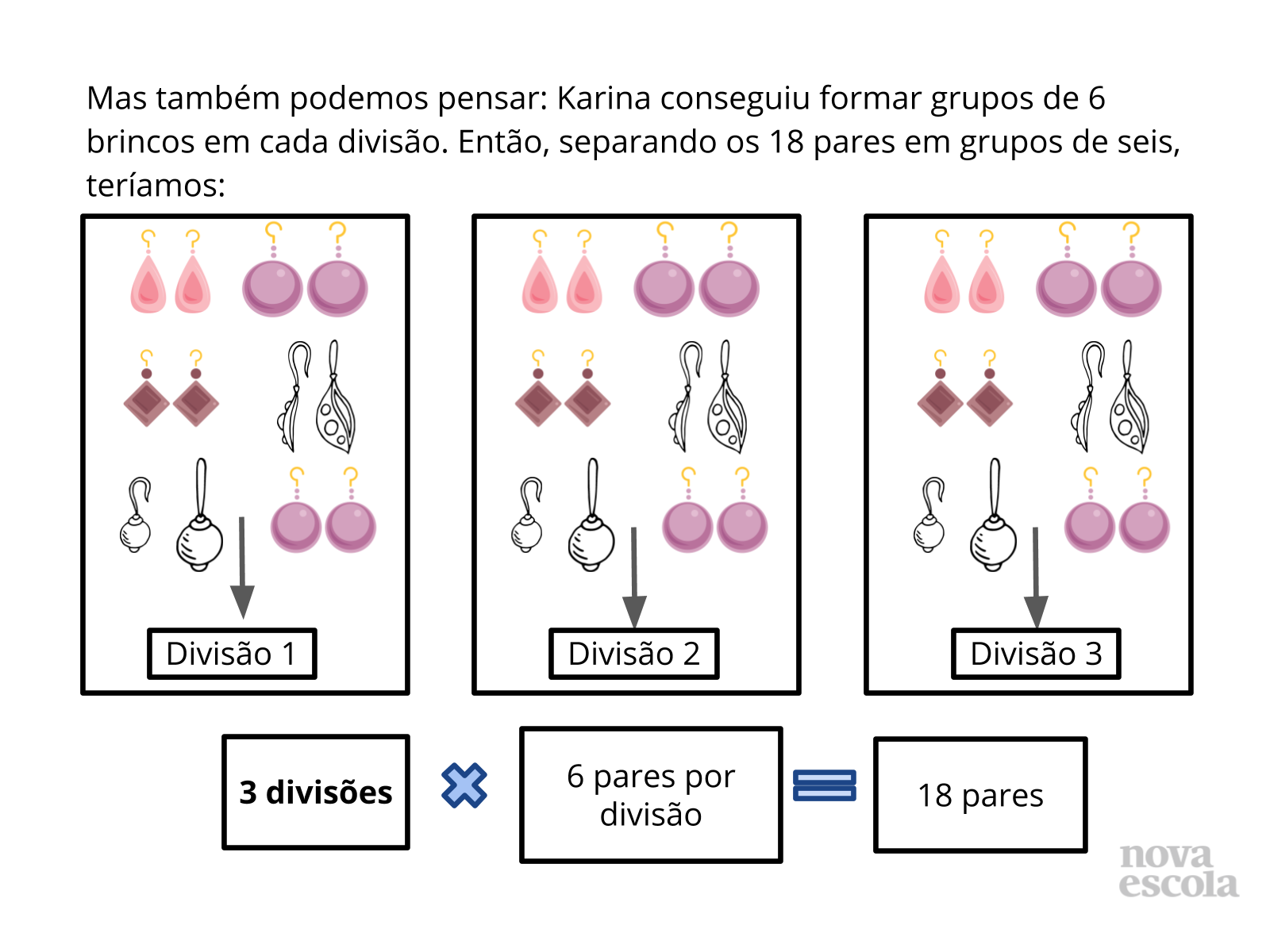
Tempo sugerido: 10 minutos. (Slides 5 a 14)
Orientação: Questione as duplas sobre as estratégias que utilizaram para resolver. Depois apresente as sugestões de solução dos slides. Destaque que para cada questão é possível pensar de diferentes formas, e elaborar diferentes estratégias para encontrar a resposta. É possível pensar por meio de uma multiplicação, ou de uma divisão. Isso é possível devido às relações inversas entre multiplicação e divisão. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Caso haja alguma solução equivocada, utilize esse momento para discutir com a turma onde ocorreu o equívoco.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos e apresentar as relações inversas entre multiplicação e divisão com resto zero.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Há mais de uma forma de resolver?
- Como podemos ter certeza de que está correto?
- Será que é possível resolver utilizando operações diferentes?
Discussão de soluções
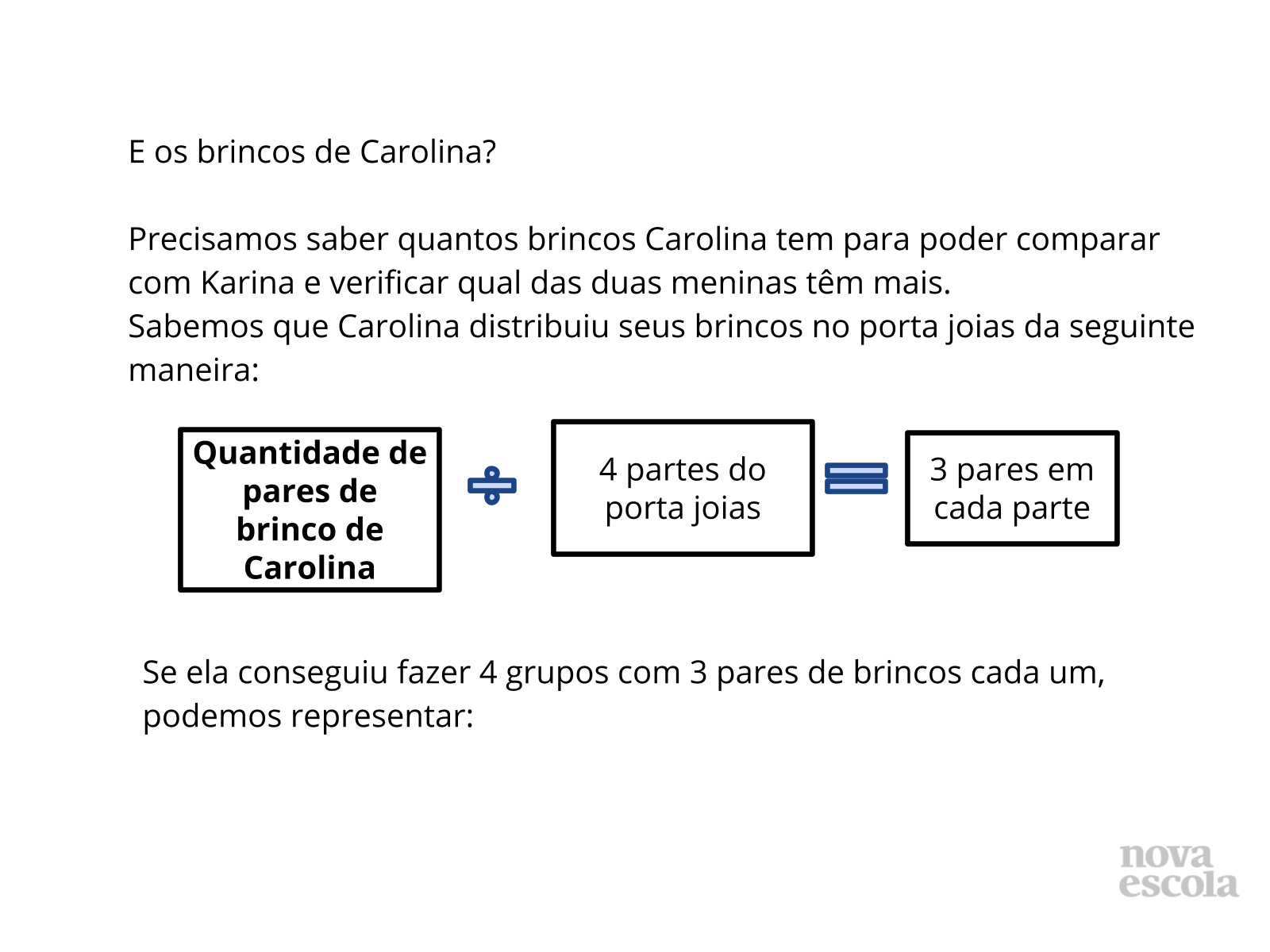
Tempo sugerido: 10 minutos. (Slides 5 a 14)
Orientação: Questione as duplas sobre as estratégias que utilizaram para resolver. Depois apresente as sugestões de solução dos slides. Destaque que para cada questão é possível pensar de diferentes formas, e elaborar diferentes estratégias para encontrar a resposta. É possível pensar por meio de uma multiplicação, ou de uma divisão. Isso é possível devido às relações inversas entre multiplicação e divisão. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Caso haja alguma solução equivocada, utilize esse momento para discutir com a turma onde ocorreu o equívoco.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos e apresentar as relações inversas entre multiplicação e divisão com resto zero.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Há mais de uma forma de resolver?
- Como podemos ter certeza de que está correto?
- Será que é possível resolver utilizando operações diferentes?
Discussão de soluções
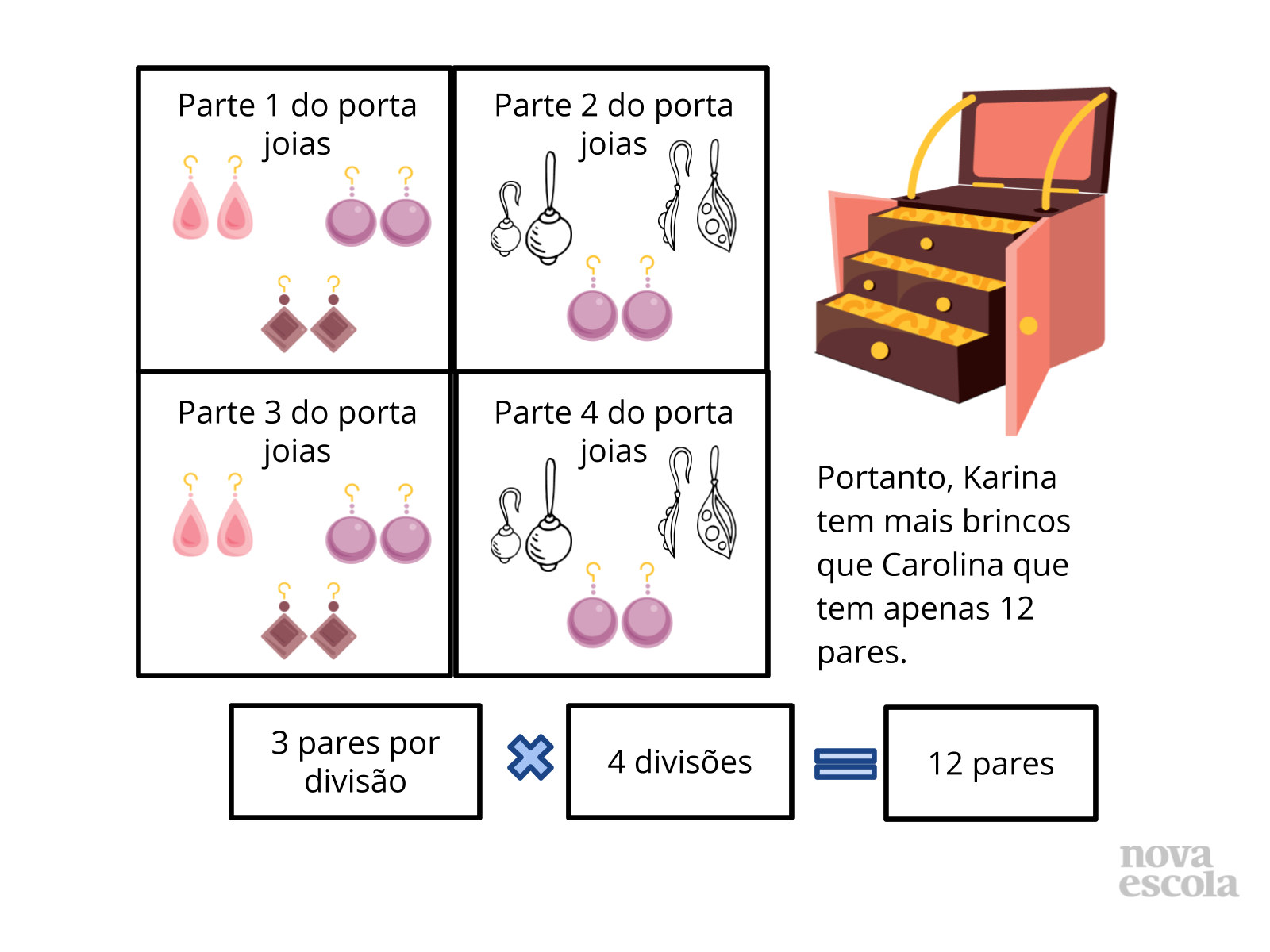
Tempo sugerido: 10 minutos. (Slides 5 a 14)
Orientação: Questione as duplas sobre as estratégias que utilizaram para resolver. Depois apresente as sugestões de solução dos slides. Destaque que para cada questão é possível pensar de diferentes formas, e elaborar diferentes estratégias para encontrar a resposta. É possível pensar por meio de uma multiplicação, ou de uma divisão. Isso é possível devido às relações inversas entre multiplicação e divisão. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Caso haja alguma solução equivocada, utilize esse momento para discutir com a turma onde ocorreu o equívoco.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos e apresentar as relações inversas entre multiplicação e divisão com resto zero.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Há mais de uma forma de resolver?
- Como podemos ter certeza de que está correto?
- Será que é possível resolver utilizando operações diferentes?
Sistematização do conceito

Tempo sugerido: 5 minutos. (Slides 15 e 16)
Orientação: Leia o conteúdo do balão com os alunos passe para o próximo slide.
Propósito: Sistematizar as relações inversas entre multiplicação e divisão com resto zero e os significados envolvidos.
Sistematização do conceito
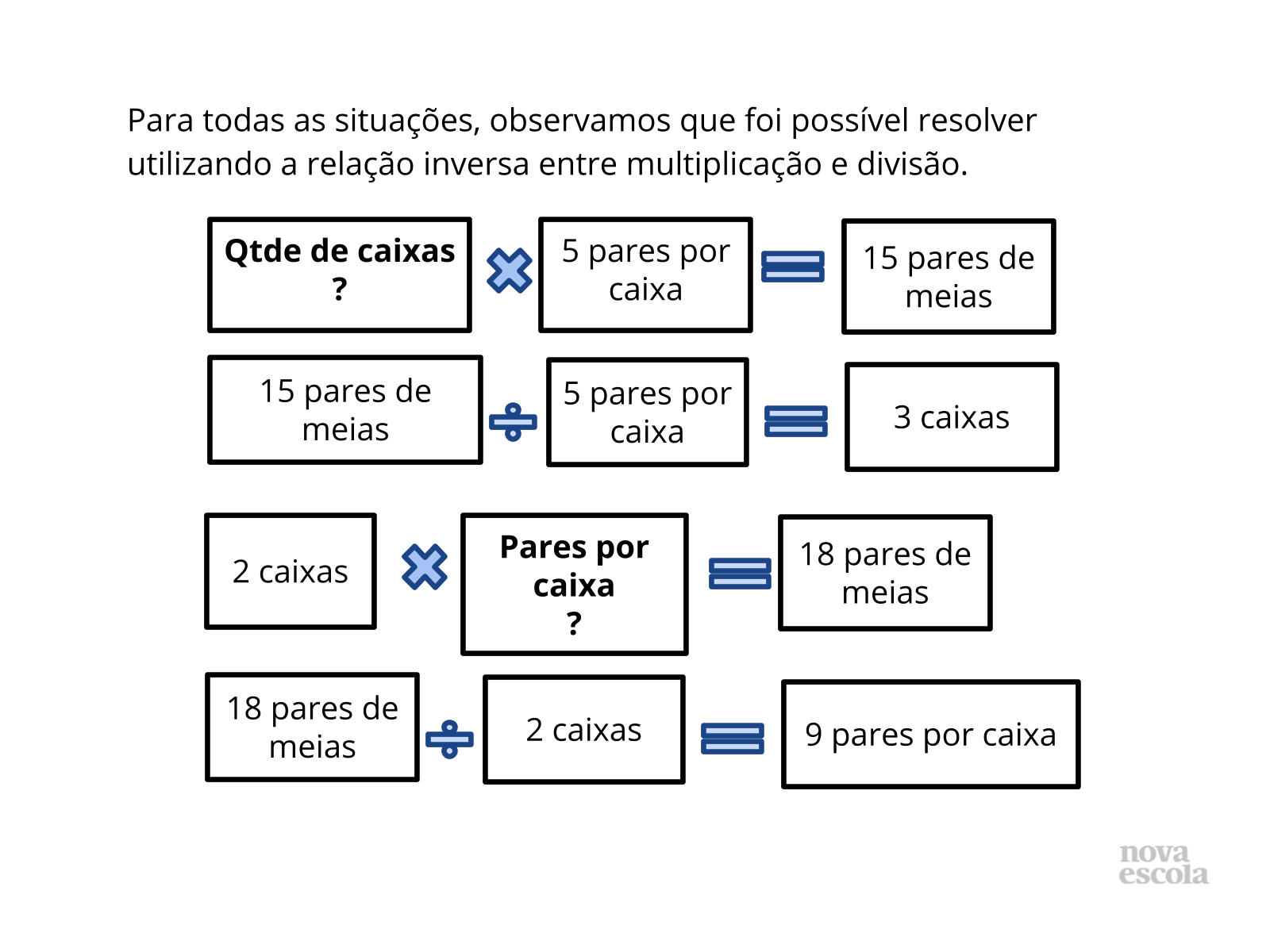
Tempo sugerido: 5 minutos. (Slides 15 e 16)
Orientação: Apresente o slide aos alunos para recordar, através de alguns exemplos trabalhados durante a aula, que foi possível pensar de diferentes formas para solucionar as questões. Destaque que o importante é estar atento às informações que são fornecidas e ao que desejamos saber. Assim podemos elaborar diferentes estratégias de solução. Pensar de maneira inversa é uma estratégia interessante em muitos casos, pois pode ser uma forma mais rápida de identificar a resposta.
Propósito: Sistematizar as relações inversas entre multiplicação e divisão com resto zero e os significados envolvidos.
Encerramento
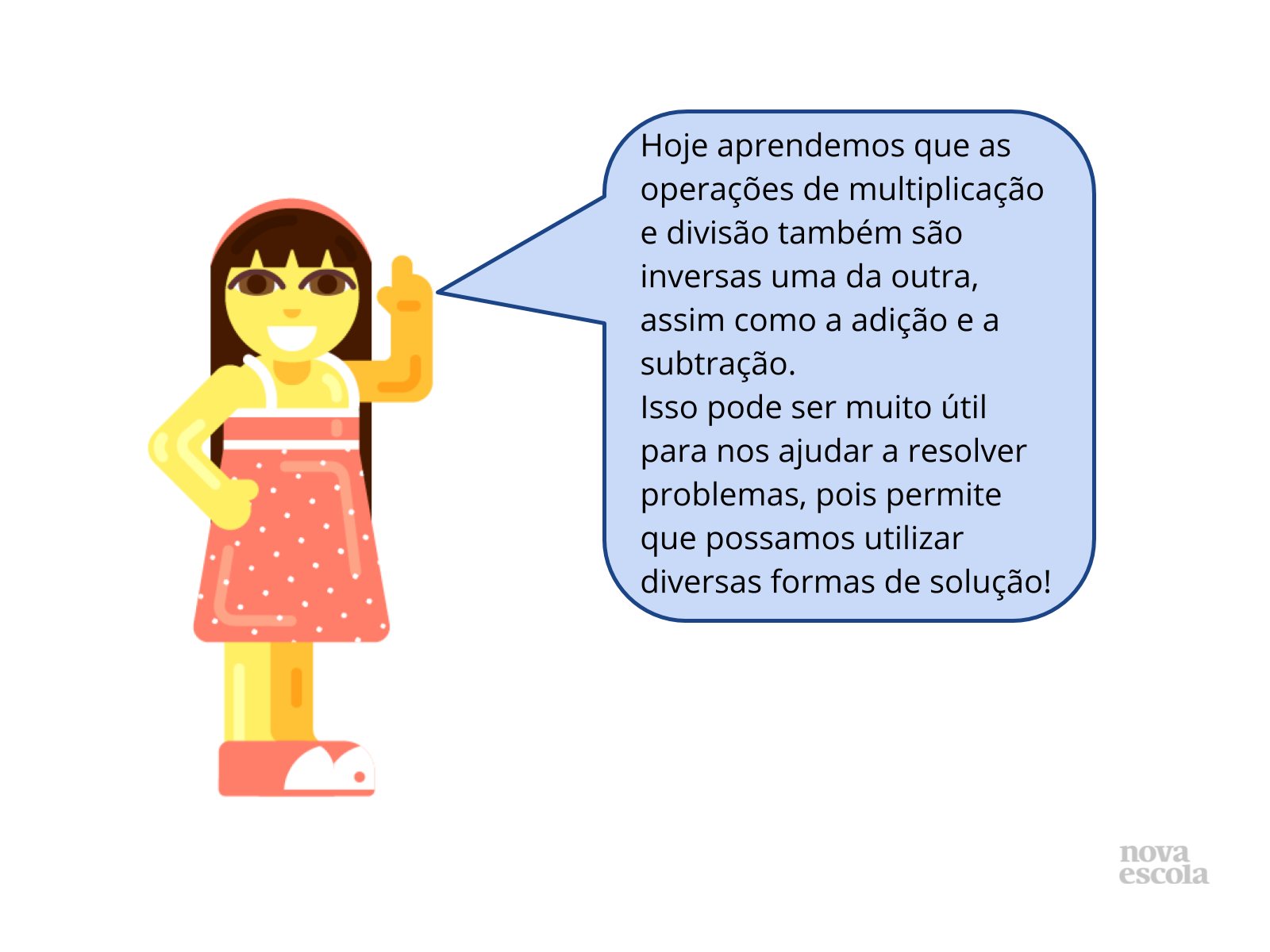
Tempo sugerido: 3 minutos.
Orientação: Leia o conteúdo do balão com os alunos e reforce que assim como acontece com as operação de adição e subtração, a multiplicação e a divisão também são operações inversas uma da outra e que saber disso pode nos ajudar muito a resolver problemas.
Propósito: Encerrar a aula resumindo o que foi estudado.
Raio X

Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem, respondendo cada uma das questões. Para isso eles devem refletir sobre o que foi estudado sobre as relações inversas entre multiplicação e divisão com resto zero.
Propósito: Aplicar as relações inversas entre multiplicação e divisão com resto zero e os significados envolvidos para resolver problemas.
Discuta com a turma:
- Como vocês estão pensando?
- Como podemos identificar que operação devemos usar?
Materiais complementares:
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_15ALG_03
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: (apenas se forem absolutamente indispensáveis; caso contrário, inserir todos como opcionais)
- Opcionais: Google Documentos, Google Apresentações, Google Formulários.
Para este plano, foque na etapa Discussão das soluções.
Aquecimento
Apresentar a atividade e pedir a eles que respondam-na, além de responderem às questões presentes nas orientações ao professor.
Atividade principal
Pedir aos alunos que resolvam a situação no caderno para discutir as soluções na etapa seguinte.
Discussão das soluções
O professor pode abrir um arquivo usando o Google Documentos para que os alunos insiram suas resoluções, as quais ficarão expostas para toda a turma acessar e conhecer as estratégias. Caso o professor perceba que uma ou outra estratégia não tenha aparecido, ele pode complementar essa etapa usando o Google Apresentações com os slides presentes nesta etapa para enviar o link aos alunos.
Caso a turma não use os recursos digitais, o professor pode fazer esse levantamento das resoluções e socializar os slides impressos após a resolução da Atividade Principal, inserindo as questões presentes nas orientações ao professor.
Sistematização
Propor aos alunos que criem uma sequência de desafios usando o Google Formulários para serem trocados com toda a turma, lembrando-os de fazer uma explicação inicial sobre o que aprenderam nesta aula. Fechar os desafios com uma pergunta sobre o que aprenderam com os desafios para que os demais colegas respondam, atendendo à etapa seguinte (Encerramento).
Encerramento
Ver etapa anterior.
Raio X
O professor pode incluir mais uma situação ao Raio X para que os alunos pratiquem um pouco mais sobre o tema abordado, seja na resolução escrita ou via Google Formulários, lembrando sempre de incluir as questões presentes nas orientações ao professor.
Convite às famílias
Convidar os alunos a criarem, junto à família, uma lista de enigmas matemáticos a partir das operações de multiplicação e divisão com resto zero como sendo inversas.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Márcia Regina Kaminski
Mentora: Carla Simone Albuquerque
Revisora Pedagógica: Eliane Zanin
Especialista de área: Sandra Regina Correa Amorim
Habilidade da BNCC
(EF04MA13) Reconhecer, por meio de investigações, utilizando a calculadora quando necessário, as relações inversas entre as operações de adição e de subtração e de multiplicação e de divisão, para aplicá-las na resolução de problemas.
Objetivos específicos
- Trabalhar as relações inversas entre multiplicação e divisão a partir de situações problemas.
- Compreender que as operações de multiplicação e divisão são inversas e que envolvem um significado.
Conceito-chave
- Investigação de padrões em operações: entre multiplicação e divisão com resto zero com os números naturais.
Vocabulário
- Multiplicação.
- Divisão.
- Inversa.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
- Lápis preto e de cor,
- Datashow ( opcional ).