Atividade principal
Plano de Aula
Plano de aula: Relações inversas entre adição e subtração
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Investigação de padrões em operações fundamentais
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Márcia Regina Kaminski
Mentora: Carla Simone Albuquerque
Revisora Pedagógica: Eliane Zanin
Especialista de área: Sandra Regina Correa Amorim
Habilidade da BNCC
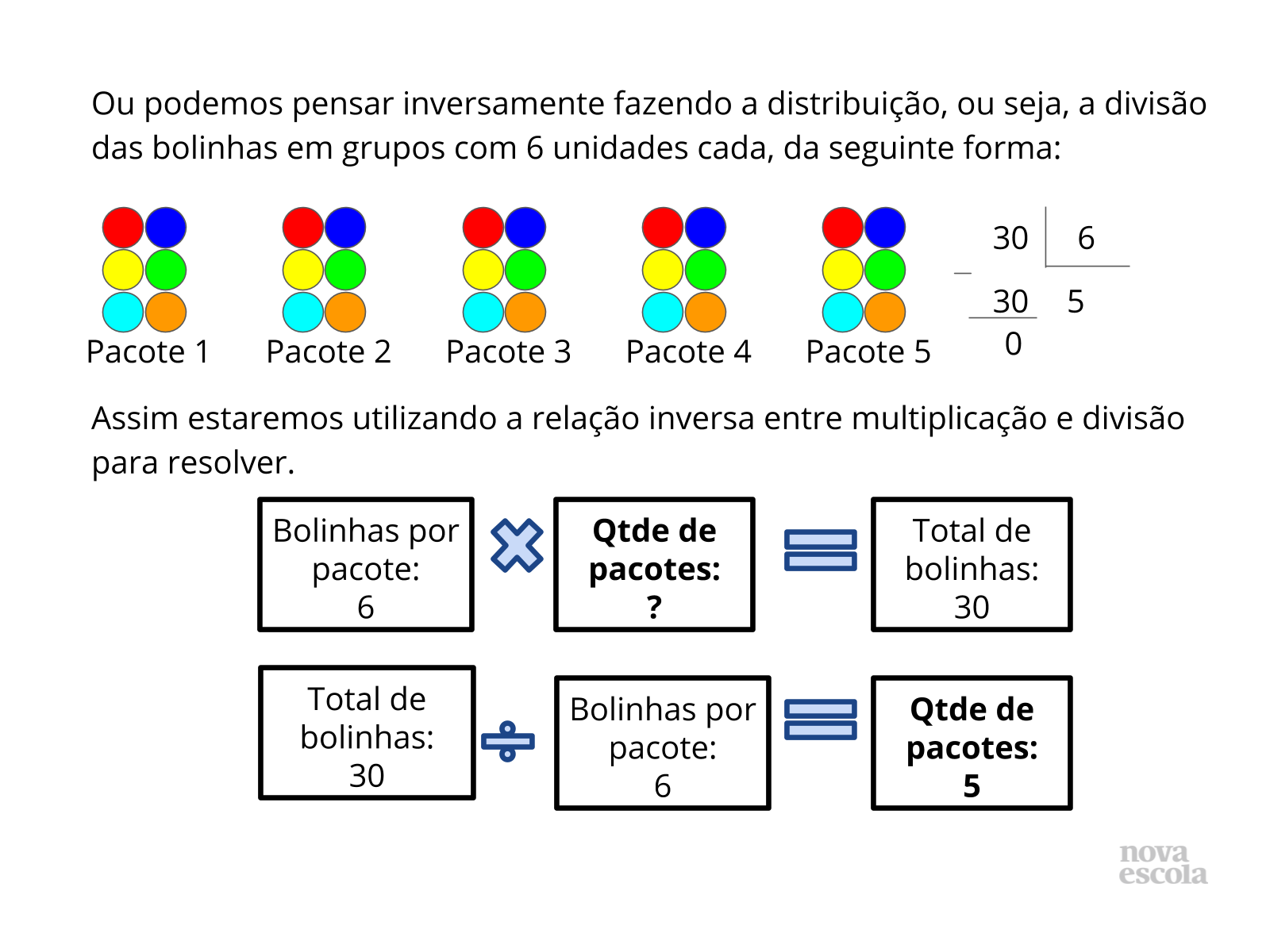
(EF04MA13) Reconhecer, por meio de investigações, utilizando a calculadora quando necessário, as relações inversas entre as operações de adição e de subtração e de multiplicação e de divisão, para aplicá-las na resolução de problemas.
Objetivos específicos
- Trabalhar as relações inversas entre adição e subtração a partir de situações- problema;
- Compreender que as operações de adição e subtração são inversas e que envolvem um significado.
Conceito-chave
- Investigação de padrões em operações: entre adição e subtração com os números naturais.
Vocabulário
- Adição.
- Subtração.
- Inversa.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
- Lápis preto e de cor;
- Datashow ( opcional ).
Habilidades BNCC:
Objetivos de aprendizagem
- Trabalhar as relações inversas entre adição e subtração a partir de situações- problema;
- Compreender que as operações de adição e subtração são inversas e que envolvem um significado.
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 5 minutos.
Orientação: Leia o conteúdo do slide com os alunos e questione o que eles acham: É possível identificar os números ocultos? De que forma podemos fazer isso? Deixe que os alunos comentem que estratégias utilizariam para identificar isso. Reserve três minutos para que os alunos tentem decifrar os enigmas. Peça que alguns alunos expliquem a forma que utilizaram para que a turma possa discutir coletivamente. Verifique se alguns alunos pensaram em utilizar as relações inversas entre adição e subtração como estratégias de solução. No primeiro caso, os alunos devem perceber que se 23 foi subtraído do número oculto, basta fazer a operação inversa, ou seja, adicionar 23 ao resultado 74 para identificar o número oculto: 74 + 23 = 97. No segundo caso, os alunos devem perceber que se 32 foi adicionado ao número oculto, basta fazer a operação inversa, ou seja, subtrair 32 do resultado 87, para identificar o número oculto:
87 - 32 = 55. Nos dois casos, o que desejamos é saber a situação inicial antes de um transformação ter acontecido. Nestes casos precisamos fazer a inversão da situação. Adicionar se foi subtraído, e subtrair se foi adicionado. Estaremos assim desfazendo a situação, para identificar como ela era anteriormente.
Propósito: Introduzir as relações inversas entre as operações de adição e subtração.
Discuta com a turma:
- Será que é possível decifrar os enigmas identificando os números ocultos?
- Como vocês fariam para saber isso?
- Seria possível resolver utilizando algum tipo de cálculo? Qual? Por quê? Como podemos ter certeza disso?
- Por onde podemos começar a pensar na solução?
Atividade principal

Tempo sugerido: 15 minutos.
Orientação: Leia as questões com os alunos e proponha que respondam, trabalhando em duplas. Permita que eles utilizem diferentes estratégias para encontrar a solução. Acompanhe o trabalho das duplas observando os caminhos utilizados por eles para resolver.
Propósito: Explorar os diferentes significados envolvidos em uma mesma operação e as relações inversas entre adição e subtração.
Discuta com a turma:
- Como podemos pensar para responder cada uma das questões?
- Por que vocês escolheram esta forma de solução?
- É possível resolver de outra maneira?
Materiais complementares:
Discussão das soluções
Tempo sugerido: 10 minutos. (Slides 5, 6, 7, 8, 9, 10 e 11)
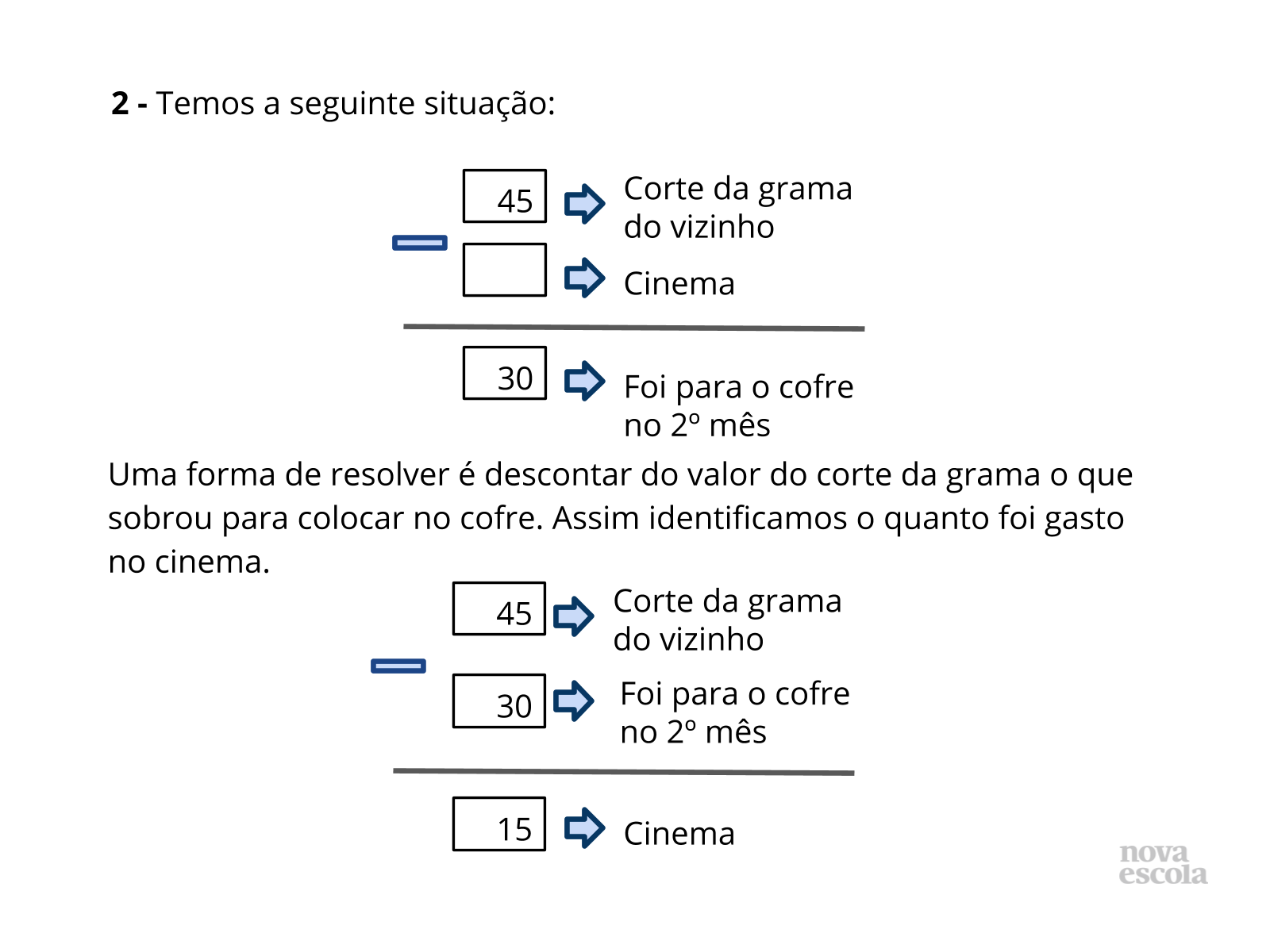
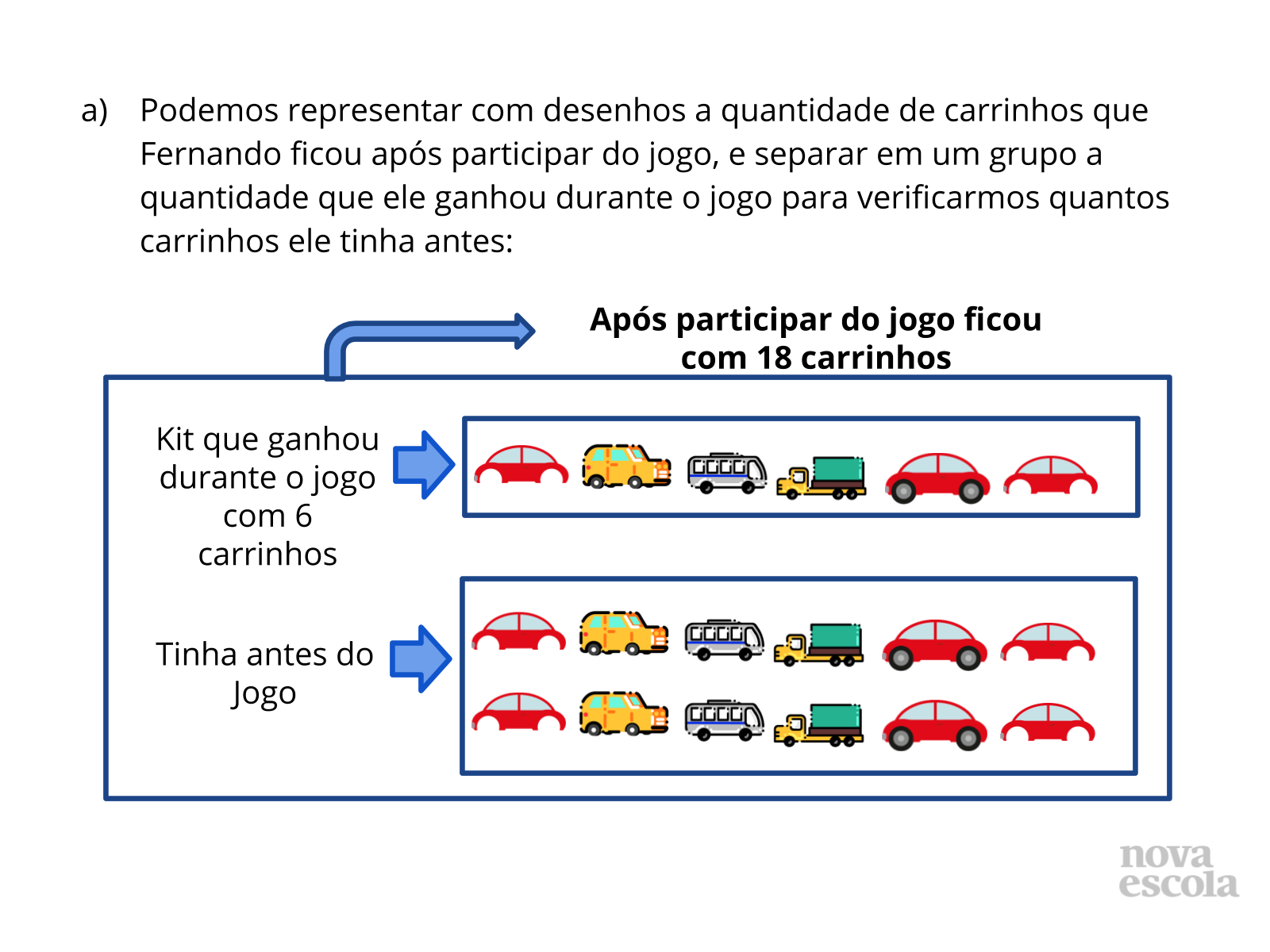
Orientação: Questione as duplas sobre como pensaram para responder cada uma das questões. Depois apresente as formas utilizadas nos slides. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Destaque que apesar da situação inicial ter sido modificada por um ganho ou acréscimo, utilizamos a subtração para resolver em função da pergunta que foi feita. Caso algum aluno tenha resolvido de outra forma, abra espaço para que ele apresente sua solução e a forma como pensou. Caso haja alguma solução equivocada, também utilize este momento para discutir com a turma onde ocorreu o engano.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Se Fernando ganhou carrinhos, por que utilizamos a subtração? Destaque que ao separarmos os carrinhos, estamos retirando os carrinhos ganhos durante o jogo do total de carrinhos que Fernando ficou após jogar. Assim é possível verificar a quantidade anterior ao jogo.
Material Complementar:
Discussão das soluções
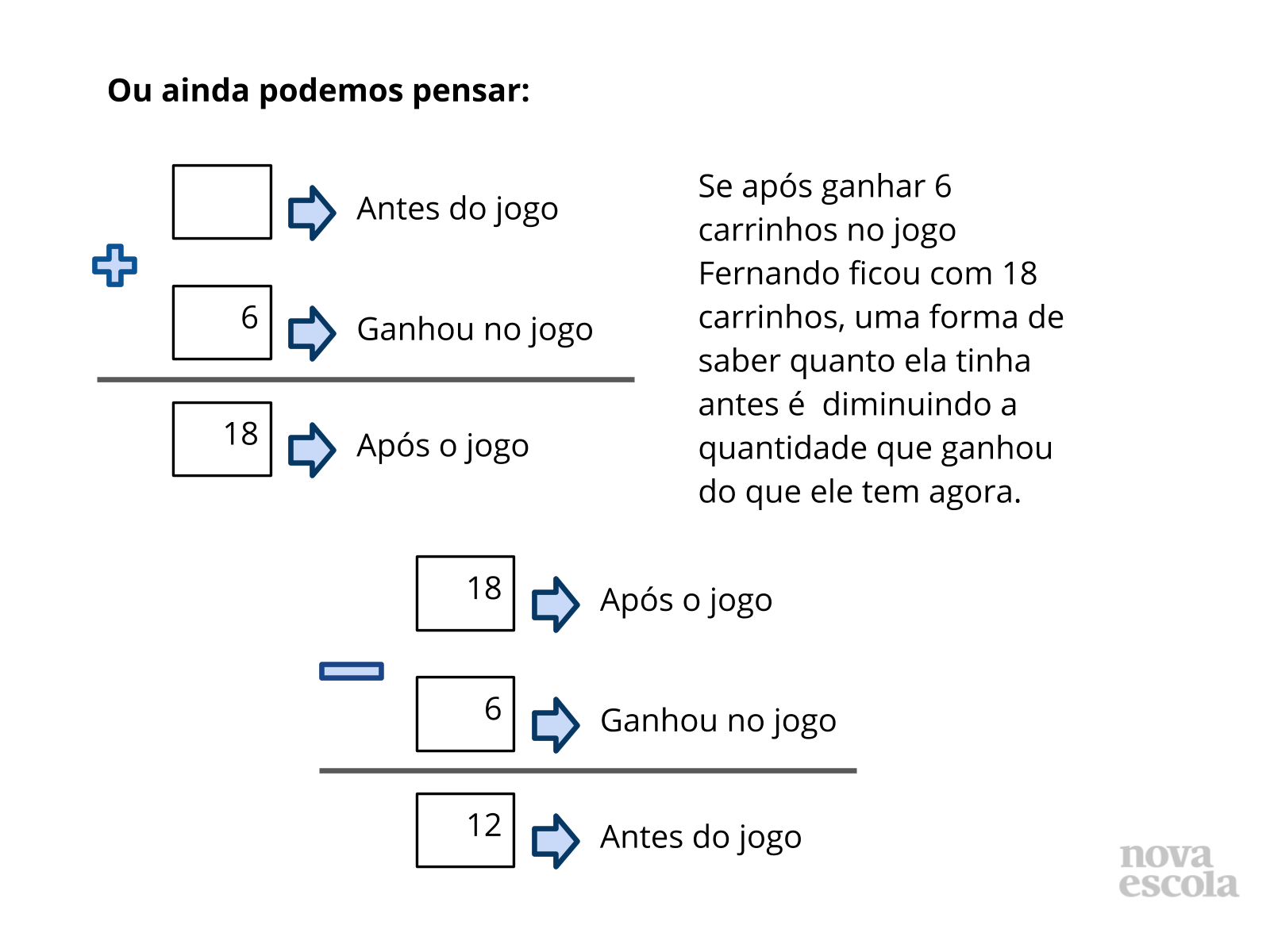
Tempo sugerido: 10 minutos. (Slides 5, 6, 7, 8, 9, 10 e 11)
Orientação: Questione as duplas sobre como pensaram para responder cada uma das questões. Depois apresente as formas utilizadas nos slides. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Destaque que apesar da situação inicial ter sido modificada por um ganho ou acréscimo, utilizamos a subtração para resolver em função da pergunta que foi feita. Caso algum aluno tenha resolvido de outra forma, abra espaço para que ele apresente sua solução e a forma como pensou. Caso haja alguma solução equivocada, também utilize este momento para discutir com a turma onde ocorreu o engano.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Se Fernando ganhou carrinhos, por que utilizamos a subtração? Destaque que ao separarmos os carrinhos, estamos retirando os carrinhos ganhos durante o jogo do total de carrinhos que Fernando ficou após jogar. Assim é possível verificar a quantidade anterior ao jogo.
Discussão das soluções
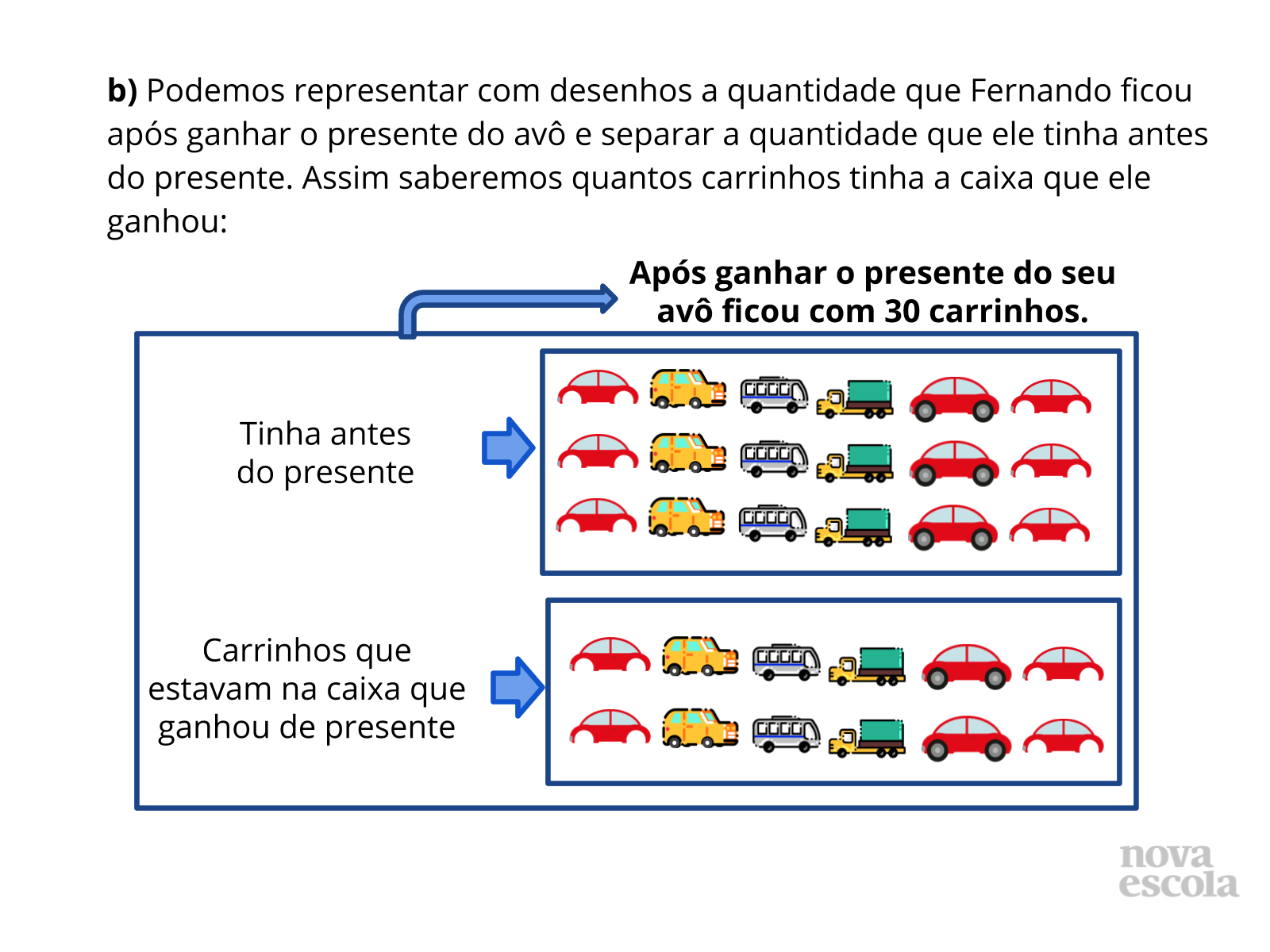
Tempo sugerido: 10 minutos. (Slides 5, 6, 7, 8, 9, 10 e 11)
Orientação: Questione as duplas sobre como pensaram para responder cada uma das questões. Depois apresente as formas utilizadas nos slides. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Destaque que apesar da situação inicial ter sido modificada por um ganho ou acréscimo, utilizamos a subtração para resolver em função da pergunta que foi feita. Caso algum aluno tenha resolvido de outra forma, abra espaço para que ele apresente sua solução e a forma como pensou. Caso haja alguma solução equivocada, também utilize este momento para discutir com a turma onde ocorreu o engano.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Por que é importante saber a quantidade de carrinhos da caixa?
- Como podemos identificar a quantidade de carrinhos da caixa?
- Se Fernando ganhou carrinhos, por que utilizamos a subtração?
Discussão das soluções
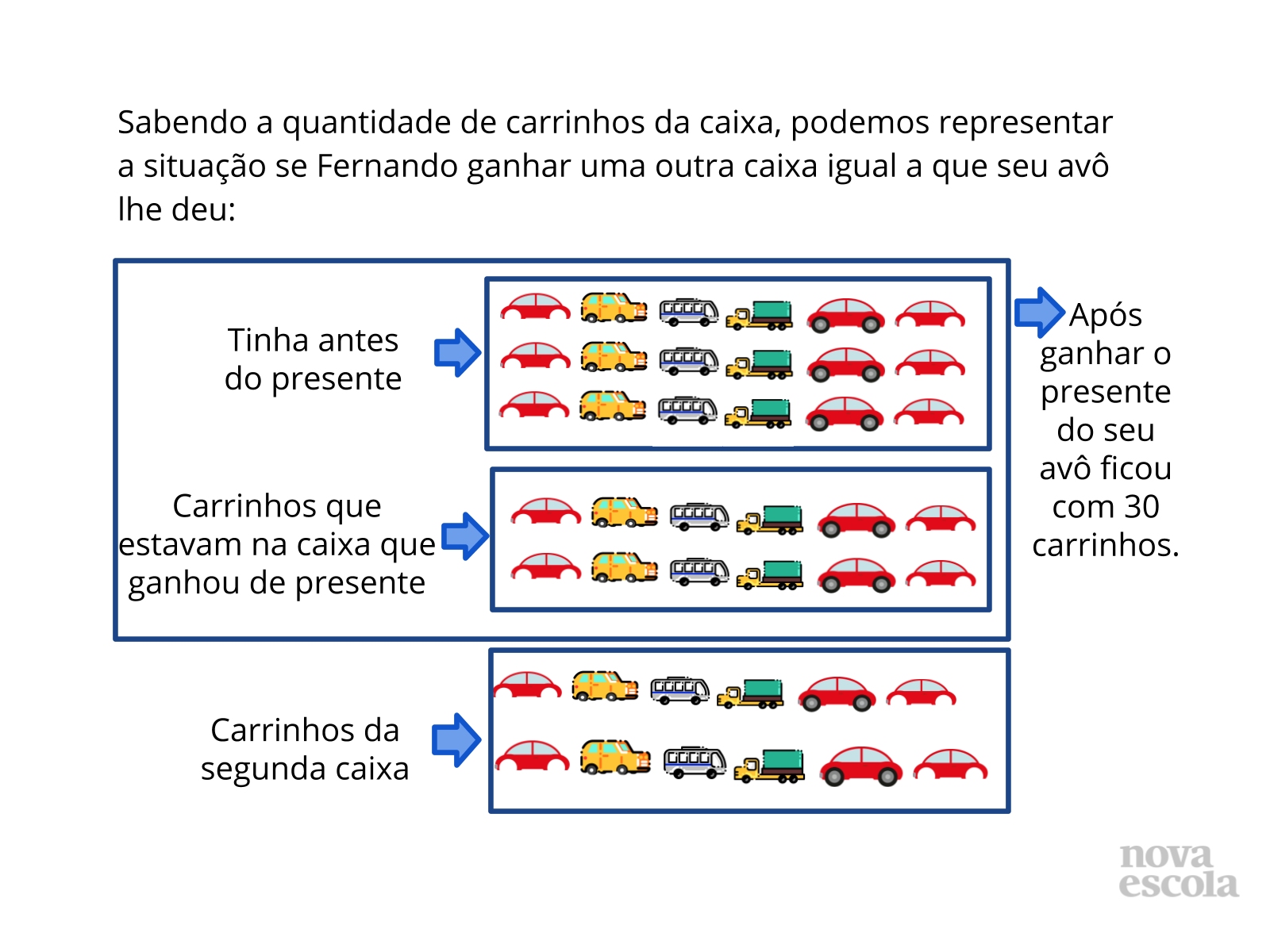
Tempo sugerido: 10 minutos. (Slides 5, 6, 7, 8, 9, 10 e 11)
Orientação: Questione as duplas sobre como pensaram para responder cada uma das questões. Depois apresente as formas utilizadas nos slides. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Destaque que apesar da situação inicial ter sido modificada por um ganho ou acréscimo, utilizamos a subtração para resolver em função da pergunta que foi feita. Caso algum aluno tenha resolvido de outra forma, abra espaço para que ele apresente sua solução e a forma como pensou. Caso haja alguma solução equivocada, também utilize este momento para discutir com a turma onde ocorreu o engano.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Por que é importante saber a quantidade de carrinhos da caixa?
- Como podemos identificar a quantidade de carrinhos da caixa?
- Se Fernando ganhou carrinhos, por que utilizamos a subtração?
Discussão das soluções
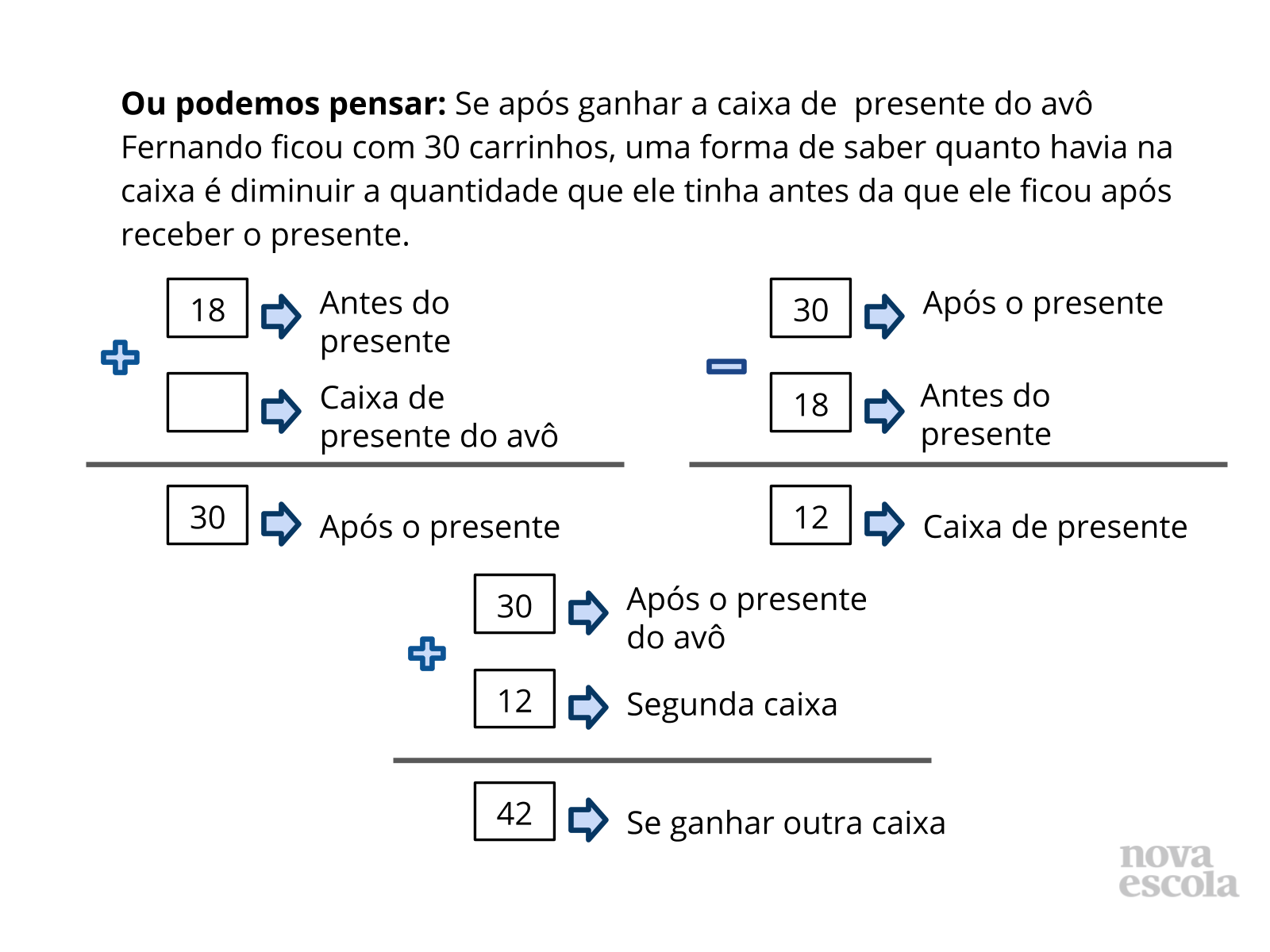
Tempo sugerido: 10 minutos. (Slides 5, 6, 7, 8, 9, 10 e 11)
Orientação: Questione as duplas sobre como pensaram para responder cada uma das questões. Depois apresente as formas utilizadas nos slides. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Destaque que apesar da situação inicial ter sido modificada por um ganho ou acréscimo, utilizamos a subtração para resolver em função da pergunta que foi feita. Caso algum aluno tenha resolvido de outra forma, abra espaço para que ele apresente sua solução e a forma como pensou. Caso haja alguma solução equivocada, também utilize este momento para discutir com a turma onde ocorreu o engano.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Se Fernando ganhou carrinhos, por que utilizamos a subtração?
Discussão das soluções
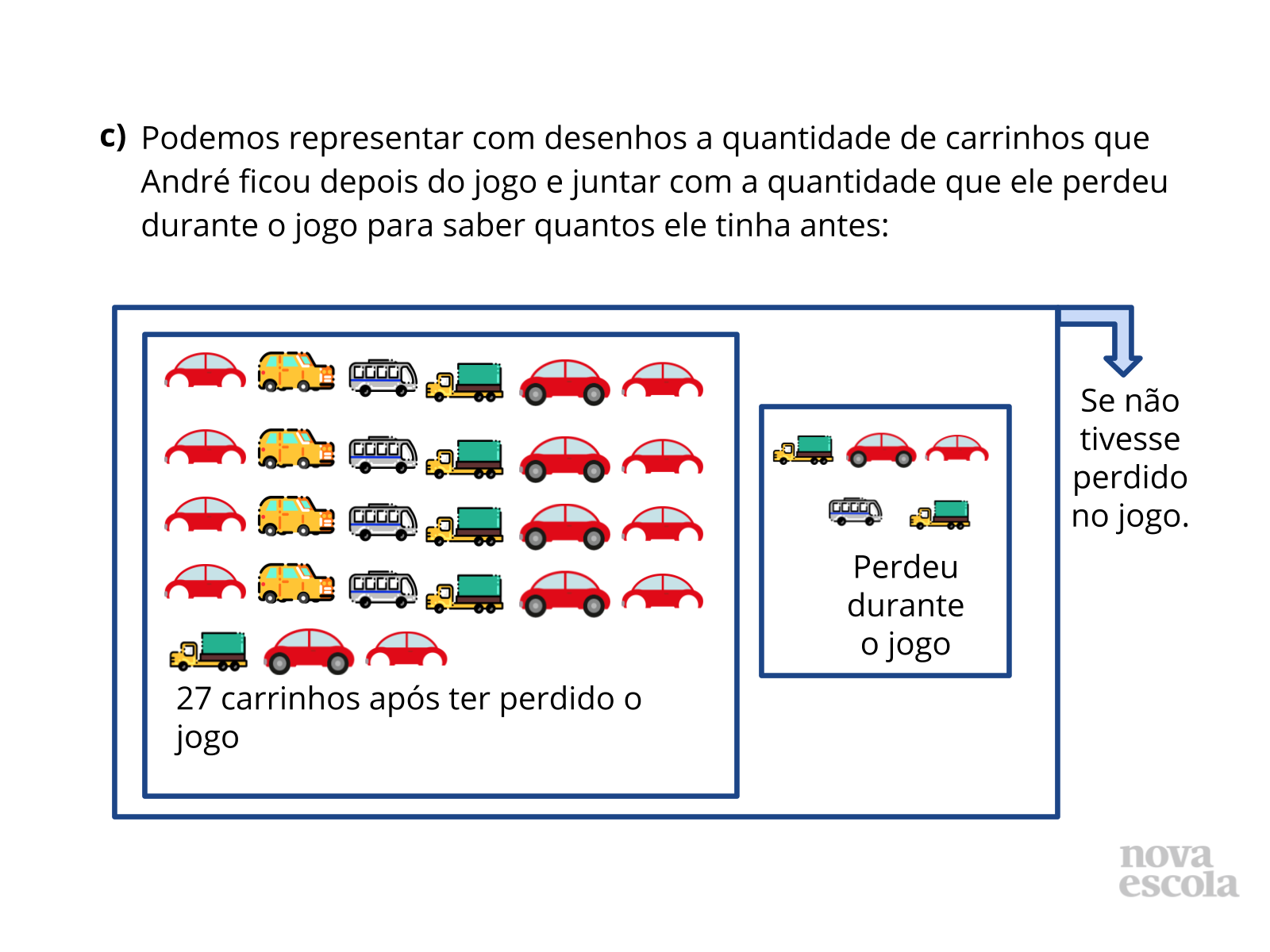
Tempo sugerido: 10 minutos. (Slides 5, 6, 7, 8, 9, 10 e 11)
Orientação: Questione as duplas sobre como pensaram para responder cada uma das questões. Depois apresente as formas utilizadas nos slides. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Destaque que apesar da situação inicial ter sido modificada por um ganho ou acréscimo, utilizamos a subtração para resolver em função da pergunta que foi feita. Caso algum aluno tenha resolvido de outra forma, abra espaço para que ele apresente sua solução e a forma como pensou. Caso haja alguma solução equivocada, também utilize este momento para discutir com a turma onde ocorreu o engano.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Se André perdeu carrinhos, por que utilizamos a adição?
Discussão das soluções
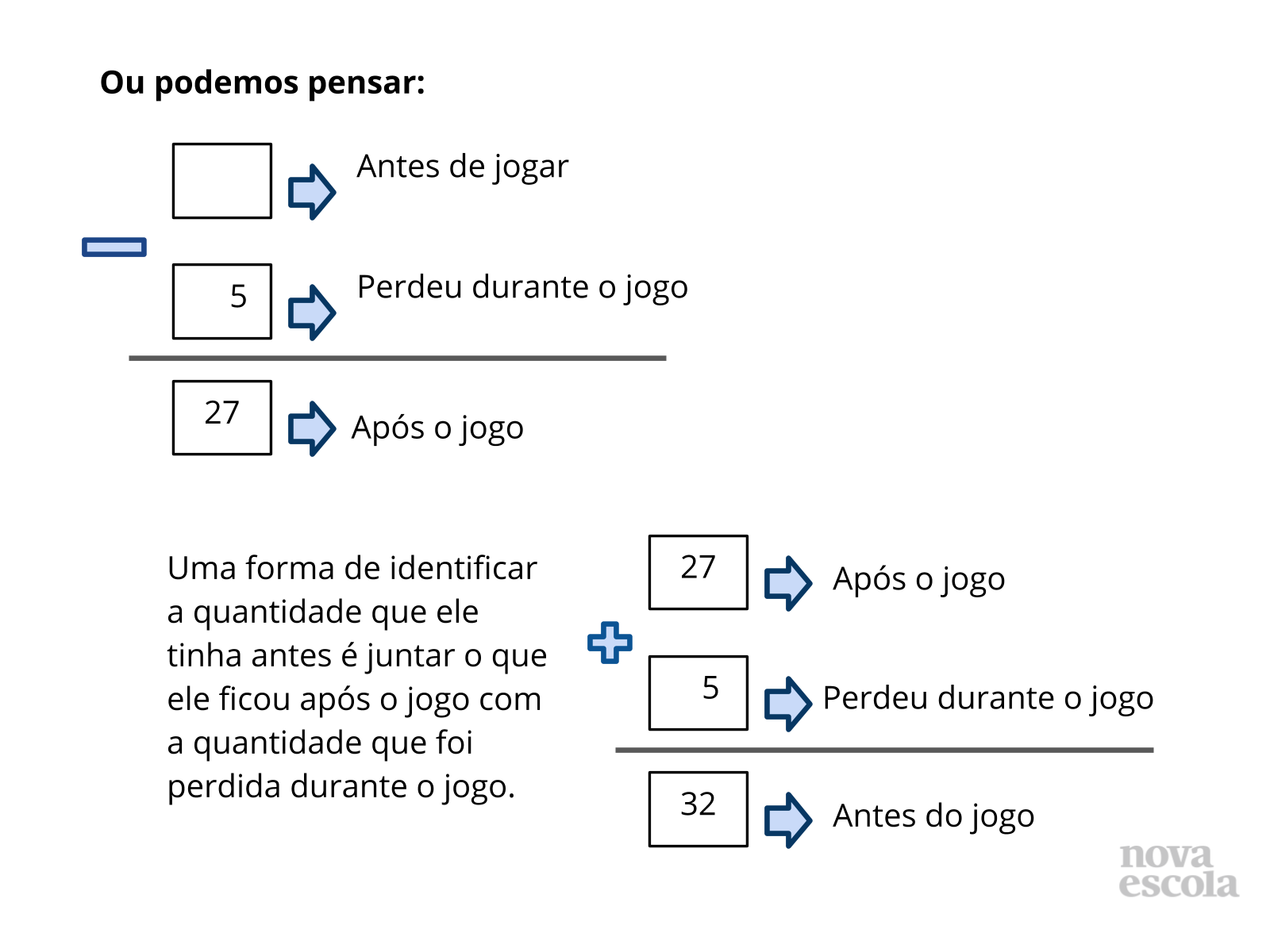
Tempo sugerido: 10 minutos. (Slides 5, 6, 7, 8, 9, 10 e 11)
Orientação: Questione as duplas sobre como pensaram para responder cada uma das questões. Depois apresente as formas utilizadas nos slides. Relacione sempre a solução feita através do esquema ou desenhos com a solução que utilizou a operação, para que os alunos compreendam o motivo da escolha de cada operação, qual o significado da operação envolvido no problema e a relação com a pergunta feita no problema. Destaque que apesar da situação inicial ter sido modificada por um ganho ou acréscimo, utilizamos a subtração para resolver em função da pergunta que foi feita. Caso algum aluno tenha resolvido de outra forma, abra espaço para que ele apresente sua solução e a forma como pensou. Caso haja alguma solução equivocada, também utilize este momento para discutir com a turma onde ocorreu o engano.
Propósito: Discutir as possíveis formas de solução encontradas pelos alunos.
Discuta com a turma:
- Como vocês pensaram para resolver? Utilizaram desenhos, esquemas? Como isso foi útil?
- É possível resolver através de algum tipo de cálculo? Qual e por quê?
- Se André perdeu carrinhos, por que utilizamos a adição?
Sistematização do conceito

Tempo sugerido: 5 minutos. (Slides 12 e 13)
Orientação: Leia o conteúdo do balão com os alunos e passe para o próximo slide.
Propósito: Sistematizar as relações inversas entre adição e subtração e os significados envolvidos.
Sistematização do conceito
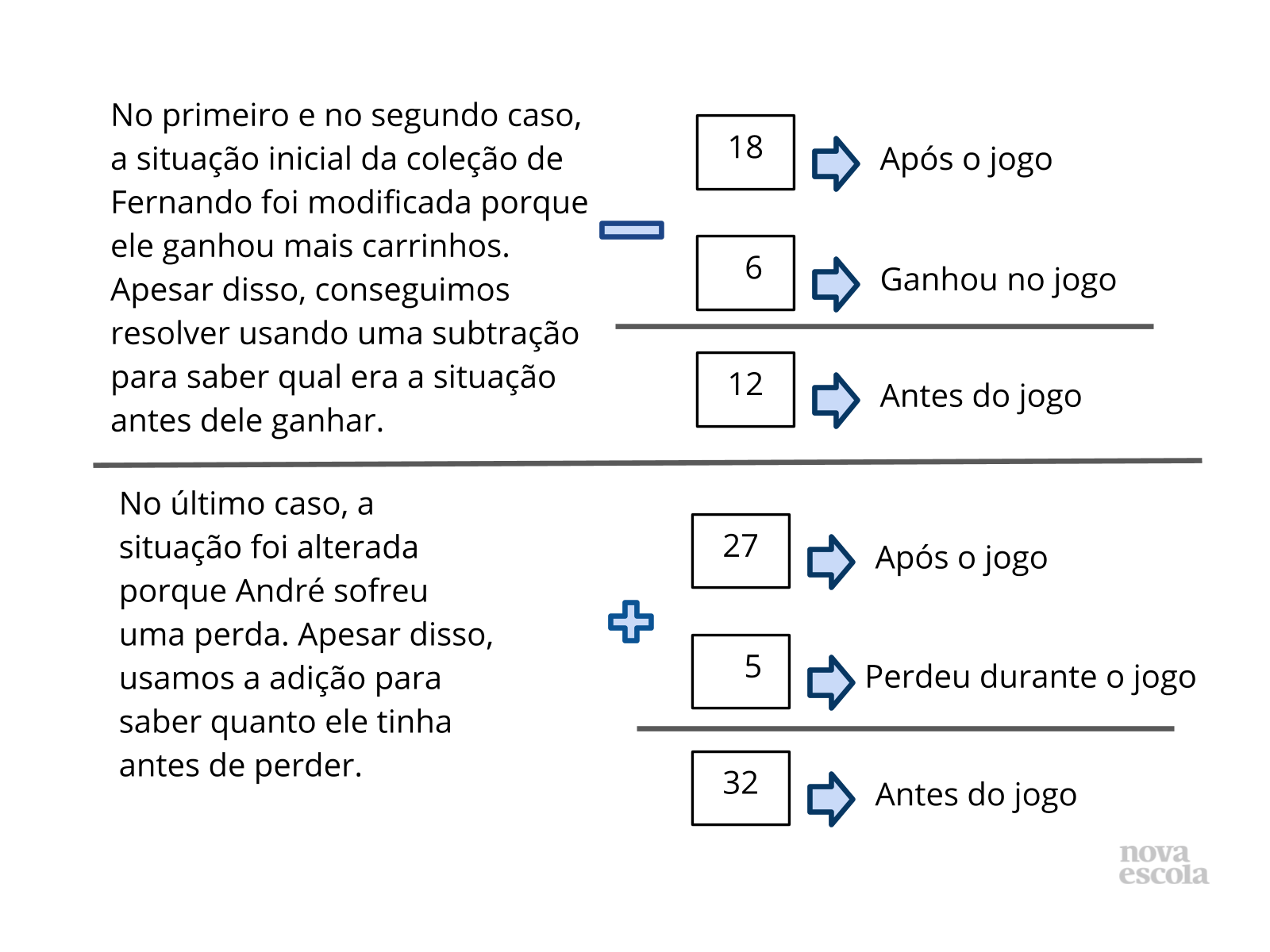
Tempo sugerido: 5 minutos. (Slides 12 e 13)
Orientação: Apresente o slide aos alunos para recordar que em cada caso usamos operações inversas à situação inicial devido ao significado envolvido e ao que precisávamos saber. Mostre que a interpretação da situação problema é muito importante para definir qual a melhor operação a ser usada. Destaque que nem sempre a palavra “ganhar” ou “perder” indicarão necessariamente que devemos usar adição ou subtração respectivamente, mas que isso será definido pelo que desejamos saber em cada caso.
Propósito: Sistematizar as relações inversas entre adição e subtração e os significados envolvidos.
Encerramento

Tempo sugerido: 3 minutos.
Orientação: Reforce de forma simples e objetiva aos alunos, que adição e subtração são operações inversas e que é muito importante ler e analisar com atenção cada situação- problema para definir qual estratégia de solução é mais adequada.
Propósito: Encerrar a aula resumindo o que foi estudado.
Raio x

Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem respondendo adequadamente cada uma das perguntas. Para isso eles devem refletir sobre o que foi estudado a respeito das relações inversas entre adição e subtração.
Propósito: Aplicar as relações inversas entre adição e subtração e os significados envolvidos para resolver situações.
Discuta com a turma:
- Como vocês estão pensando?
- Como podemos identificar que operação devemos usar?
Materiais complementares:
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_15ALG_01
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: (apenas se forem absolutamente indispensáveis; caso contrário, inserir todos como opcionais)
- Opcionais: Google Meet, Google Formulários, Google Apresentações, YouTube.
Para este plano, foque na etapa Atividade Principal.
Aquecimento
O professor pode lançar os enigmas encaminhando por e-mail aos alunos e, posteriormente abrindo uma discussão via Google Meet sobre o tema, com as questões propostas nas orientações.
Caso não tenham o recurso digital, o professor pode propor a resolução dos enigmas por escrito e, posteriormente inserir as questões das orientações para que os alunos reflitam sobre o que estão fazendo.
Atividade principal
Propor aos alunos que resolvam a situação de mais de uma forma, seja por registro escrito ou pelo Google Documentos, onde os alunos podem digitar seu raciocínio, além de inserirem registros fotográficos de suas resoluções.
Discussão das soluções
O professor pode socializar as resoluções dos alunos usando o Google Apresentações ou em um momento com toda a turma via Google Meet.
Sistematização
O professor pode criar um vídeo no YouTube apresentando a sistematização para que os alunos consultem sempre que for preciso.
Caso a turma não tenha acesso ao recurso, isso pode ser feito de maneira impressa. Unir essa etapa à próxima (Encerramento).
Encerramento
Ver etapa anterior.
Raio X
Apresentar as questões impressas ou via Google Formulários, inserindo as questões problematizadoras presentes nas orientações ao professor.
Convite às famílias
Convidar as famílias a construírem um banco de questões que se assemelham às estudadas nesta aula para compor a problemoteca pessoal do aluno, que pode ser física ou virtual.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Márcia Regina Kaminski
Mentora: Carla Simone Albuquerque
Revisora Pedagógica: Eliane Zanin
Especialista de área: Sandra Regina Correa Amorim
Habilidade da BNCC
(EF04MA13) Reconhecer, por meio de investigações, utilizando a calculadora quando necessário, as relações inversas entre as operações de adição e de subtração e de multiplicação e de divisão, para aplicá-las na resolução de problemas.
Objetivos específicos
- Trabalhar as relações inversas entre adição e subtração a partir de situações- problema;
- Compreender que as operações de adição e subtração são inversas e que envolvem um significado.
Conceito-chave
- Investigação de padrões em operações: entre adição e subtração com os números naturais.
Vocabulário
- Adição.
- Subtração.
- Inversa.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
- Lápis preto e de cor;
- Datashow ( opcional ).