Sugestão de adaptação para ensino remoto
Código do plano
MAT6_19GRMO05
Recursos
- Necessários: Folha sulfite, lápis, caderno
- Opcionais: Meet, Zoom, WhatsApp, Google sala de Aula
Introdução ao volume: https://pt.khanacademy.org/math/basic-geo/basic-geo-volume-sa/volume-rect-prism/v/how-we-measure-volume
Sistema Internacional de medidas: http://www.inmetro.gov.br/consumidor/pdf/Resumo_SI.pdf
Para este plano, foque na etapa: Atividade Principal
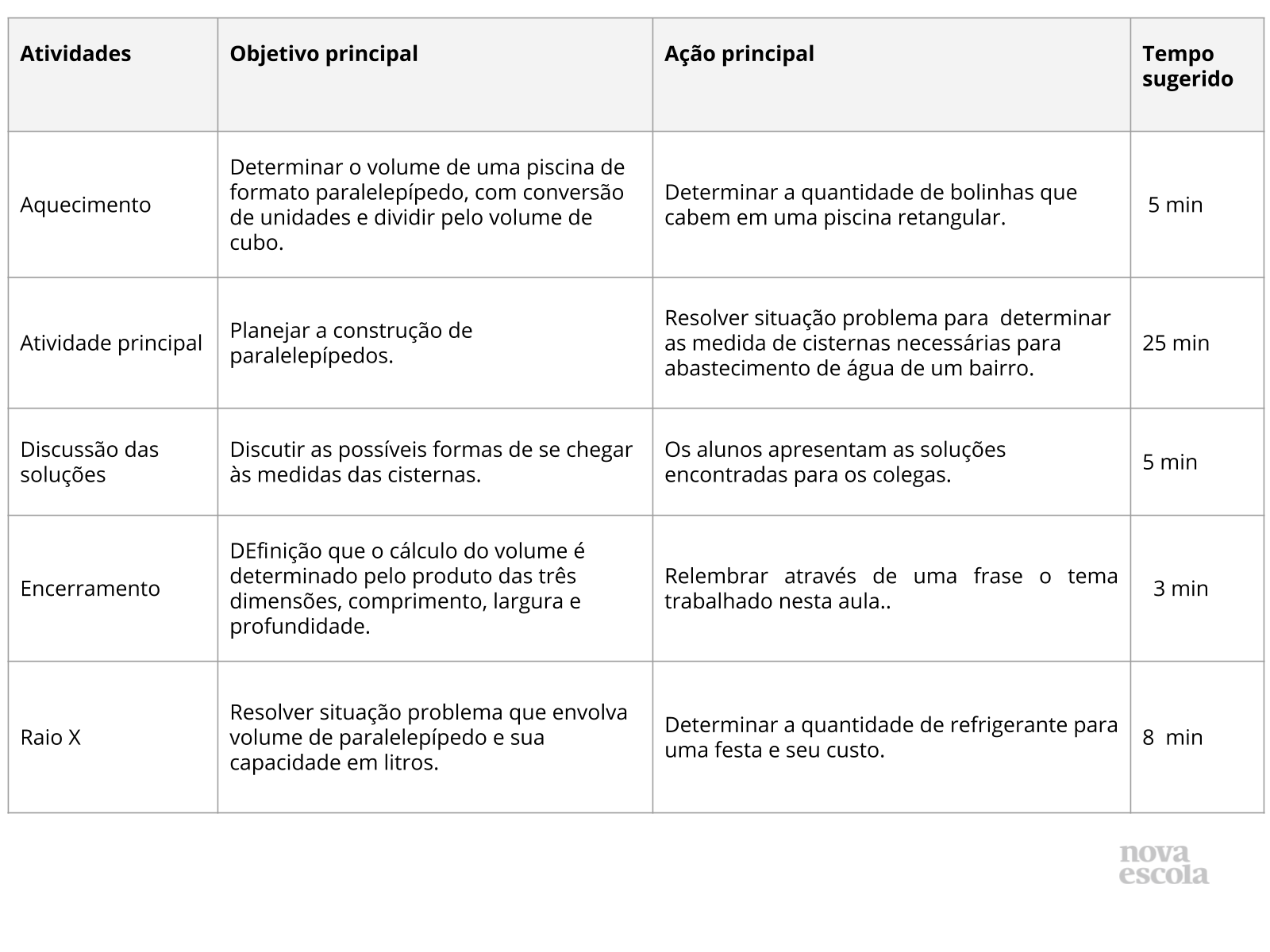
Aquecimento
Você pode disponibilizar aos alunos (via WhatsApp) o slide do Aquecimento que é uma preparação para Atividade Principal.
Atividade Principal (adaptada)
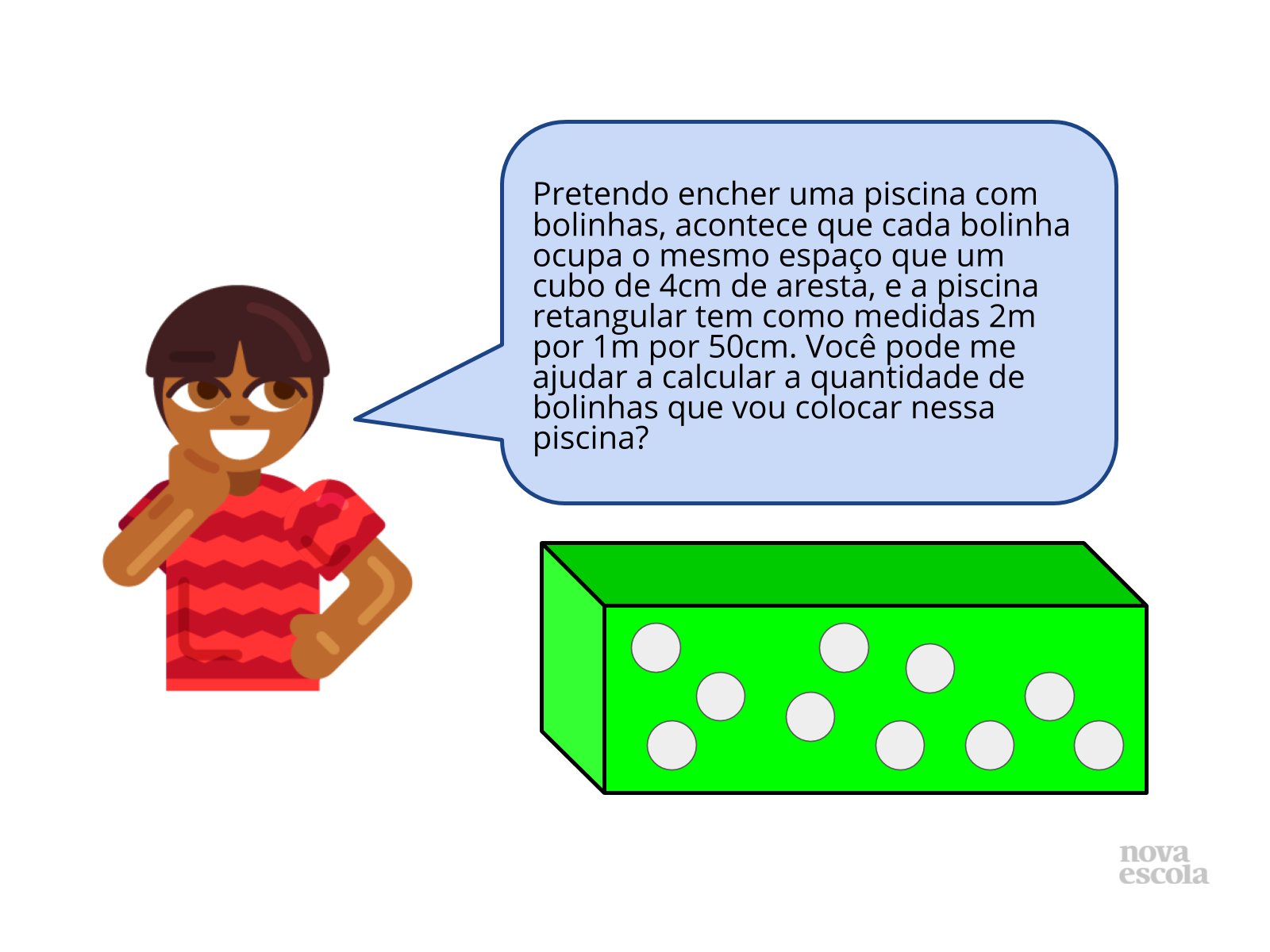
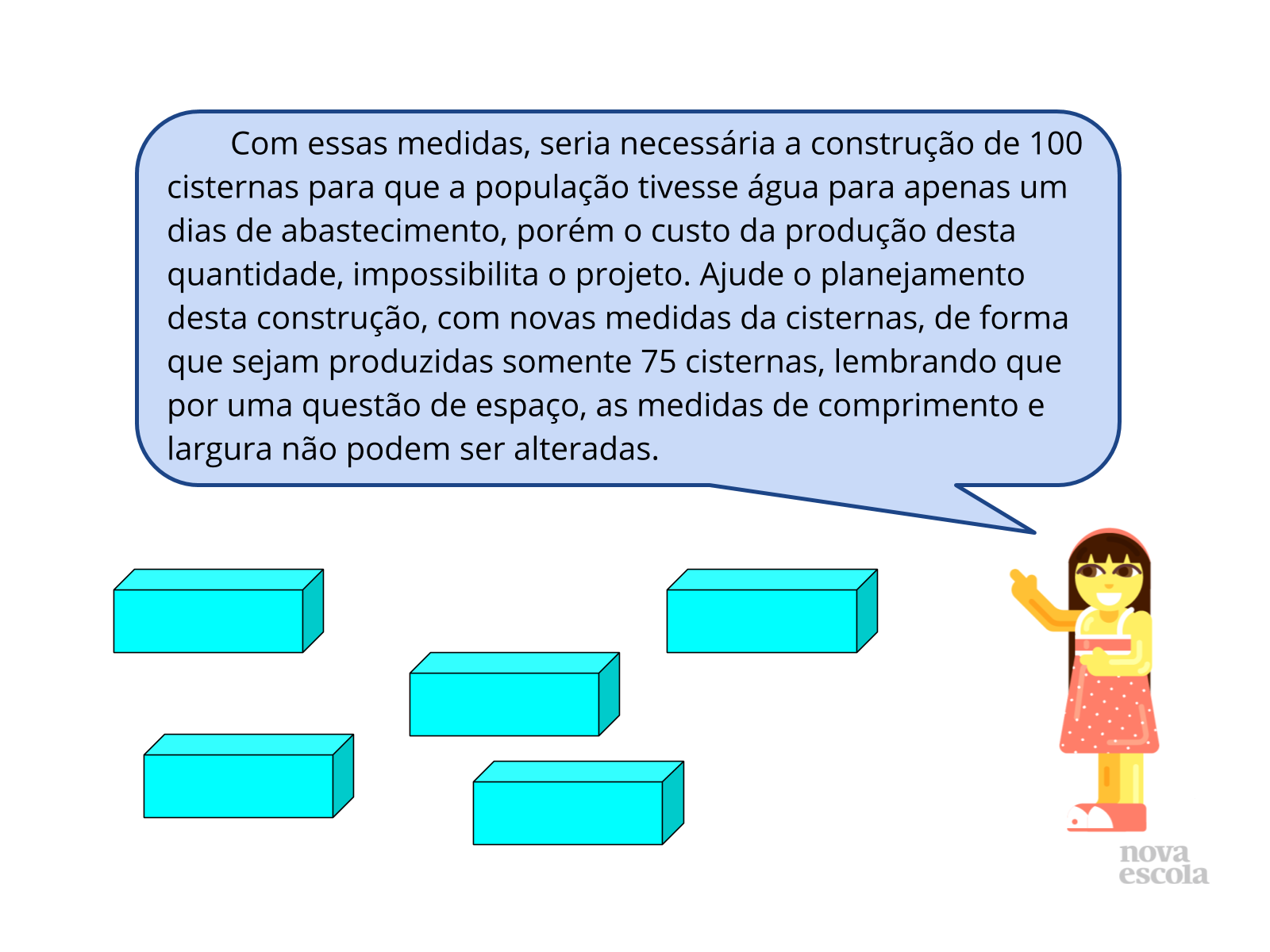
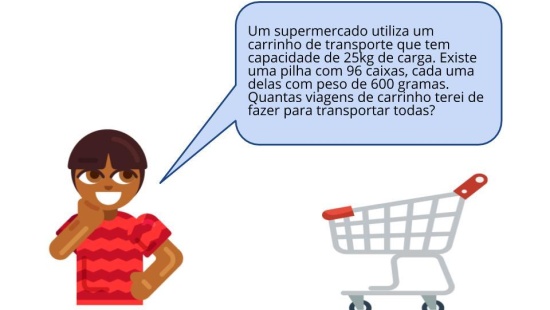
Professor, o foco da atividade é o volume do paralelepípedo. Para isso, os alunos vão precisar vivenciar algumas etapas para essa aula. É importante que você encaminhe orientações, via áudio ou vídeo (por WhatsApp), focando nessas informações (ver slides 4 a 6). Sugerimos que você encaminhe a atividade principal (versão impressa) para os alunos realizarem, solicitando que eles deem um retorno da atividade. É interessante manter um canal de comunicação para dúvidas e esclarecimentos. Oriente-os a fotografar as suas estratégias e respostas para compartilhar com o professor e a turma no momento da discussão das soluções.
Se sua aula fora assíncrona, deixe a tarefa na escola ou envie pelo WhatsApp. Grave um áudio explicando e peçam que enviem para você combinando um retorno de devolutiva. Nesse retorno, você pode enviar o print com registros dos outros alunos para que eles comparem com suas estratégias e colem no seu caderno como repertório de soluções.
Para saber mais sobre a aula e auxiliar no encaminhamento das atividades, sugira os links:
Onde mais se consome água no Brasil: https://exame.com/brasil/onde-mais-se-consome-agua-no-brasil/
Volume de um prisma retangular: https://pt.khanacademy.org/math/basic-geo/basic-geo-volume-sa/volume-rect-prism/v/volume-of-a-rectangular-prism-or-box-examples
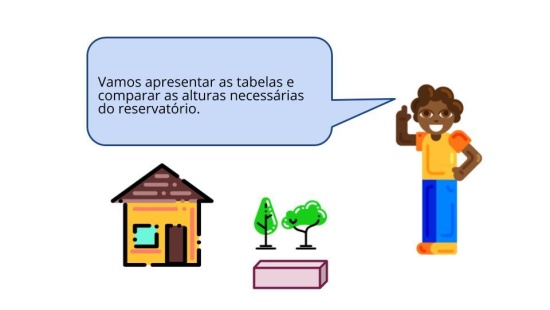
Discussão das soluções
Professor, esse é um dos momentos mais importantes da aula, portanto fique atento às respostas dos alunos. Observe as informações nas discussões das soluções desse plano de aula (slides). Escolha o que você vai discutir de forma síncrona e que pode servir de referência para seu feedback à turma. Considere, sobretudo, as respostas dos alunos para observar erros e estratégias adotadas e assim, poder reorientar o estudo e dar dica a para a realização de novas atividades (Raio X e atividades complementares).
Se sua aula for assíncrona, envie as explicações por mensagens de áudio pelo WhatsApp.
Raio X
Use o Raio X e as atividades complementares como forma de revisão para consolidação das aprendizagens. Não esqueça de retomar discussões também dessas atividades e focar nos pontos de aprendizagem mais críticos.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
 Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.