Guia de intervenções
Plano de Aula
Plano de aula: Analisando eventos Aleatórios
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Análise de chances de eventos aleatórios
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Cristiano Santos Rodrigues
Mentor: Edicleia Xavier da Costa
Especialista de área: Rita Batista
Habilidade da BNCC
EF04MA26 - Identificar, entre eventos aleatórios cotidianos, aqueles que têm maior chance de ocorrência, reconhecendo características de resultados mais prováveis, sem utilizar frações.
Objetivo específico
Compreender melhor a análise de eventos aleatórios e trabalhar com as possibilidades de um espaço amostral.
Conceito-chave
Aleatoriedade
Recursos necessários
- Papel
- Lápis
- Borracha
- Lousa
- Atividades projetadas em formato de slides ou impressas.
Habilidades BNCC:
Objetivos de aprendizagem
Resumo da aula
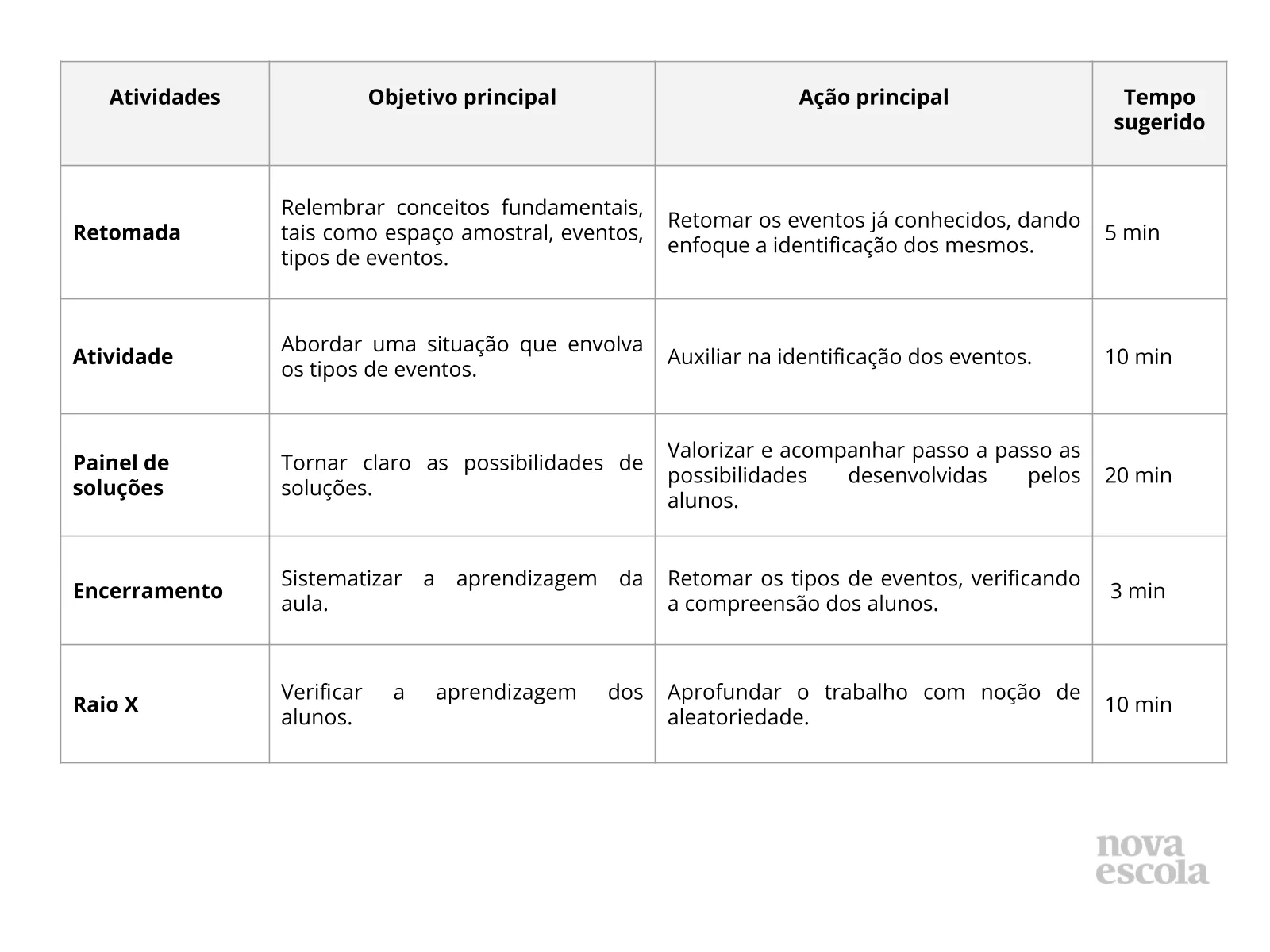 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo previsto: 5 minutos.
Orientações: Professor, aproveite a retomada para verificar o entendimento da turma sobre probabilidade. É importante que tenham facilidade em diferenciar em uma determinada situação qual o espaço amostral, o evento definido, e qual tipo de evento é o solicitado. Percebendo que uma mesma situação pode admitir diferentes possibilidades.
Propósito: Retomar conceitos probabilísticos.
Discuta com a turma:
- Vocês conseguem diferenciar os tipos de eventos?
- Já ouviu falar em evento certo, evento nulo ou evento provável?
Atividade Principal
Tempo Sugerido: 10 min (Slides 4 e 5)
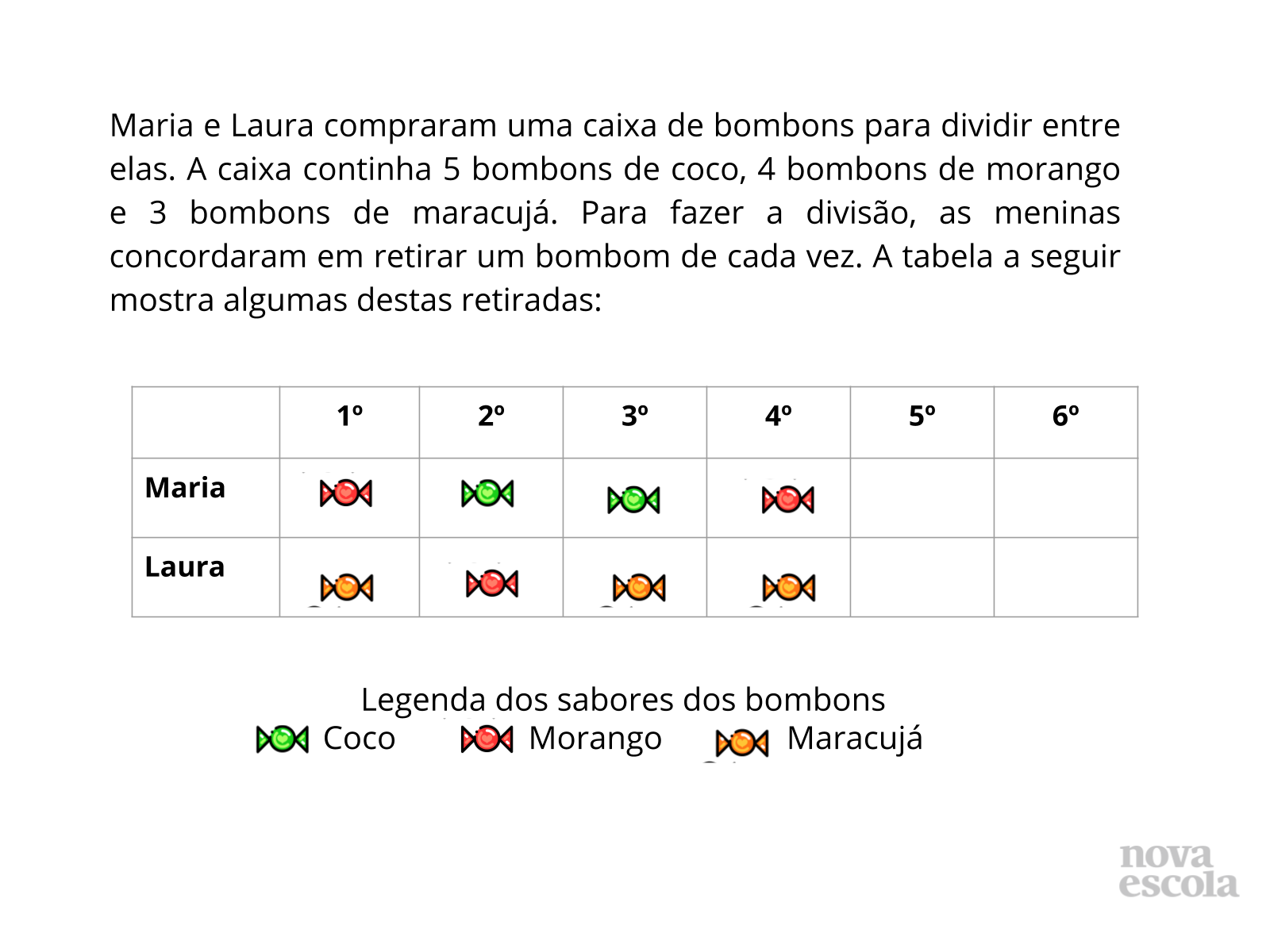
Orientações: Professor, deixe que o aluno leia individualmente a situação, analisando sua compreensão da situação proposta. Nesse primeiro momento, vamos sugerir que destaque as informações que considera importante, identificando qual foi seu entendimento dos dados tabelados, o que eles indicam. Discuta a situação proposta, o que eles acham que compõe o espaço amostral na atividade. Para as perguntas propostas, o aluno terá que observar o espaço amostral que compõem a situação, os bombons que foram retirados e os que restam, assim para cada alternativa definirá a probabilidade de retirada do evento citado. Com essa situação problema, os alunos irão identificar que um mesmo espaço amostral pode admitir diferentes possibilidades de soluções, além de tipos de eventos variados, dependendo da probabilidade de ocorrência procurada.Você pode fazer o download desta atividade para imprimir para os seus alunos.
Utilize o guia de intervenções para discutir com a turma os tipos de eventos abordados.
Propósito: Desenvolver uma situação que permita vivenciar variados tipos de eventos.
Discuta com a turma:
- Quais elementos compõem o espaço amostral desta situação?
- A cada retirada o que ocorre com o espaço amostral? Ele é alterado?
- Qual é o evento solicitado em cada item?
Materiais complementares para impressão:
Atividade Principal

Tempo Sugerido: 10 min (Slides 4 e 5)
Orientações: Professor, deixe que o aluno leia individualmente a situação, analisando sua compreensão da situação proposta. Nesse primeiro momento, vamos sugerir que destaque as informações que considera importante, identificando qual foi seu entendimento dos dados tabelados, o que eles indicam. Discuta a situação proposta, o que eles acham que compõe o espaço amostral na atividade. Para as perguntas propostas, o aluno terá que observar o espaço amostral que compõem a situação, os bombons que foram retirados e os que restam, assim para cada alternativa definirá a probabilidade de retirada do evento citado. Com essa situação problema, os alunos irão identificar que um mesmo espaço amostral pode admitir diferentes possibilidades de soluções, além de tipos de eventos variados, dependendo da probabilidade de ocorrência procurada.Você pode fazer o download desta atividade para imprimir para os seus alunos.
Utilize o guia de intervenções para discutir com a turma os tipos de eventos abordados.
Propósito: Desenvolver uma situação que permita vivenciar variados tipos de eventos.
Discuta com a turma:
- Quais elementos compõem o espaço amostral desta situação?
- A cada retirada o que ocorre com o espaço amostral? Ele é alterado?
- Qual é o evento solicitado em cada item?
Discussão da Solução

Tempo Sugerido: 20 minutos (slides 6, 7 e 8)
Orientações: Na sequência dos slides, estão apresentadas algumas soluções para o problema. Antes de discuti-las com a turma, deixe que apresentem suas considerações e estratégias. É importante ver o entendimento dos alunos sobre a situação apresentada. Discuta com eles as possibilidades que formam o espaço amostral.
Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides, nelas encontrará algumas formas de resolução da atividade. O primeiro passo é que o aluno identifique o espaço amostral, assim saberá quais as possibilidades existentes. Para a pergunta proposta em A, o aluno terá que verificar nas retiradas realizadas, quantas vezes o bombom de maracujá aparece, para isso deve analisar a tabela que ilustra as retiradas feitas pelas meninas. Oriente os alunos a destacarem os dados importantes, focando no evento solicitado em cada pergunta.
Para a pergunta proposta em B, o aluno deve associar as quantidades existentes de cada sabor, e quantos já foram retirados, assim saberá as possibilidades do evento solicitado ocorrer.
Para a pergunta feita em C, em que as retiradas seriam refeitas, o aluno terá que considerar o espaço amostral dado, identificando a probabilidade de Maria retirar um bombom de coco, como temos 5 bombons nesse sabor, a probabilidade é indicada por 5 em 12.
Se tiver projetor a sua disposição, você pode usar os slides no lugar do quadro.
Propósito: Realizar um fechamento das ideias discutidas até o momento.
Discuta com a turma:
- Todos alunos encontraram a mesma probabilidade?
- Quais eventos temos na situação proposta?
- Você acha que uma mesma situação pode ter mais de um evento?
Discussão da Solução
Tempo Sugerido: 20 minutos (slides 6, 7 e 8)
Orientações: Na sequência dos slides, estão apresentadas algumas soluções para o problema. Antes de discuti-las com a turma, deixe que apresentem suas considerações e estratégias. É importante ver o entendimento dos alunos sobre a situação apresentada. Discuta com eles as possibilidades que formam o espaço amostral.
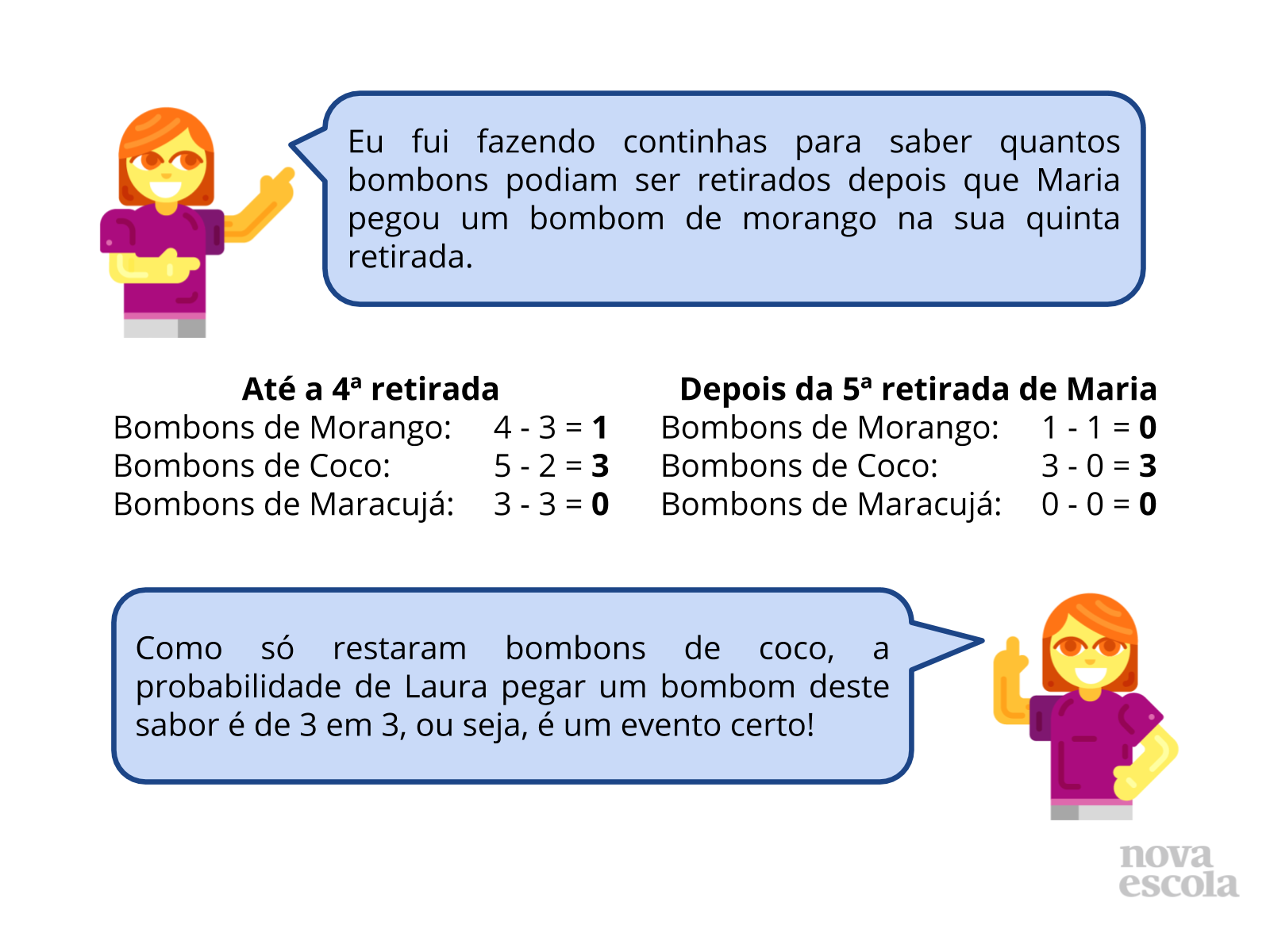
Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides, nelas encontrará algumas formas de resolução da atividade. O primeiro passo é que o aluno identifique o espaço amostral, assim saberá quais as possibilidades existentes. Para a pergunta proposta em A, o aluno terá que verificar nas retiradas realizadas, quantas vezes o bombom de maracujá aparece, para isso deve analisar a tabela que ilustra as retiradas feitas pelas meninas. Oriente os alunos a destacarem os dados importantes, focando no evento solicitado em cada pergunta.
Para a pergunta proposta em B, o aluno deve associar as quantidades existentes de cada sabor, e quantos já foram retirados, assim saberá as possibilidades do evento solicitado ocorrer.
Para a pergunta feita em C, em que as retiradas seriam refeitas, o aluno terá que considerar o espaço amostral dado, identificando a probabilidade de Maria retirar um bombom de coco, como temos 5 bombons nesse sabor, a probabilidade é indicada por 5 em 12.
Se tiver projetor a sua disposição, você pode usar os slides no lugar do quadro.
Propósito: Realizar um fechamento das ideias discutidas até o momento.
Discuta com a turma:
- Todos alunos encontraram a mesma probabilidade?
- Quais eventos temos na situação proposta?
- Você acha que uma mesma situação pode ter mais de um evento?
Discussão da Solução
Tempo Sugerido: 20 minutos (slides 6, 7 e 8)
Orientações: Na sequência dos slides, estão apresentadas algumas soluções para o problema. Antes de discuti-las com a turma, deixe que apresentem suas considerações e estratégias. É importante ver o entendimento dos alunos sobre a situação apresentada. Discuta com eles as possibilidades que formam o espaço amostral.
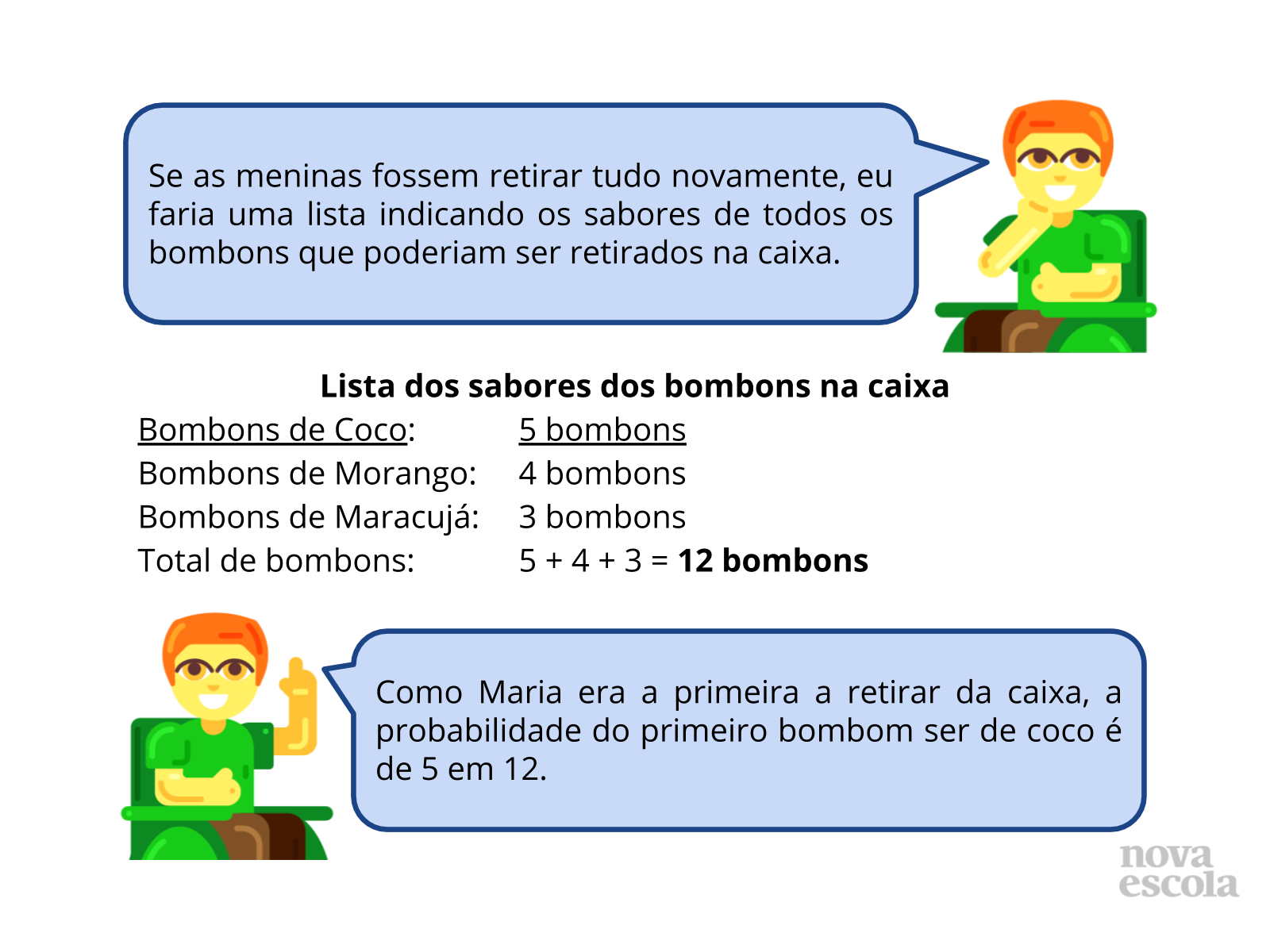
Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides, nelas encontrará algumas formas de resolução da atividade. O primeiro passo é que o aluno identifique o espaço amostral, assim saberá quais as possibilidades existentes. Para a pergunta proposta em A, o aluno terá que verificar nas retiradas realizadas, quantas vezes o bombom de maracujá aparece, para isso deve analisar a tabela que ilustra as retiradas feitas pelas meninas. Oriente os alunos a destacarem os dados importantes, focando no evento solicitado em cada pergunta.
Para a pergunta proposta em B, o aluno deve associar as quantidades existentes de cada sabor, e quantos já foram retirados, assim saberá as possibilidades do evento solicitado ocorrer.
Para a pergunta feita em C, em que as retiradas seriam refeitas, o aluno terá que considerar o espaço amostral dado, identificando a probabilidade de Maria retirar um bombom de coco, como temos 5 bombons nesse sabor, a probabilidade é indicada por 5 em 12.
Se tiver projetor a sua disposição, você pode usar os slides no lugar do quadro.
Propósito: Realizar um fechamento das ideias discutidas até o momento.
Discuta com a turma:
- Todos alunos encontraram a mesma probabilidade?
- Quais eventos temos na situação proposta?
- Você acha que uma mesma situação pode ter mais de um evento?
Encerramento

Tempo sugerido: 3 minutos
Orientação: O professor realiza aos alunos a pergunta proposta no slide, deixando eles refletirem e exporem suas opiniões oralmente. O objetivo é a retomada dos conceitos abordados na aula, percebendo a compreensão da turma em relação ao objetivo proposto. Professor, nesse momento defina com os alunos os tipos de eventos abordados. Na atividade principal temos o evento possível, certo e o impossível, aproveite para melhor exemplificá-los. Veja que um mesmo espaço amostral admite eventos variados, dependendo de que possibilidades estamos explorando dentro deste.
Discuta com a turma:
- Quando lançamos um dado, qual a probabilidade de sair um número menor que 3? (Resp.: Temos nesse caso um evento possível, em que o evento é composto pelos números 1 e 2).
- Se lançarmos o mesmo dado qual a probabilidade de sair um número maior que 6? (Resp.: Nesse caso temos um evento impossível, pois nosso espaço amostral não é composto por números maiores que 6, logo não podemos definir um evento maior que o espaço amostral ).
- E lançando o dado novamente, qual a probabilidade do número obtido ser menor que 7? (Resp.: Nesse caso temos um evento certo, pois o evento é o próprio espaço amostral).
Propósito: Promover o encerramento das ideias abordadas.
Raio X

Orientações: Deixe que o aluno individualmente leia a questão proposta. Para a atividade, ele terá que definir as possibilidades de siglas existentes, e identificar entre estas quais não iniciam-se pela letra C. Para a pergunta feita em B, o aluno terá que associar que as opções de formação de sigla só permitem as duas consoantes, logo não há probabilidade de a sigla ser iniciada por outra letra, temos um evento impossível. Você pode fazer o download desta atividade para imprimir para os seus alunos.
Utilize o guia de intervenções para discutir com os alunos as possibilidades de formação.
Propósito: Verificar a aprendizagem dos alunos.
Discuta com a turma:
- Como pode ser definido o espaço amostral desta situação?
- Você acha que alterando os nomes dos personagens interfere na quantidade de siglas?
- Quais tipos de eventos você encontrou nesta situação?
Materiais complementares para impressão:
Resolução da atividade complementar
Cálculo da probabilidade em eventos aleatórios
Para o professor
Para o aluno
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_26PES_05
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: (apenas se forem absolutamente indispensáveis; caso contrário, inserir todos como opcionais)
- Opcionais: Google Documentos, Google Apresentações, Google Formulários, Google Planilhas.
Para este plano, foque na etapa Atividade Principal.
Retomada
Propor aos alunos que pesquisem uma definição sobre os 3 tipos de eventos estudados até o momento: evento nulo, evento certo e evento provável. Esta pesquisa pode ser feita conversando com os familiares que residem na mesma casa, usando a internet ou as tarefas já estudadas em aulas anteriores.
Após a pesquisa, pedir que eles registrem uma explicação para cada tipo de evento. Isso pode ser feito em folha para envio ao professor ou usando o Google Documentos, permitindo ao professor inserir comentários para possíveis ajustes nas definições.
Atividade principal
Propor que os alunos respondam à questão indicada nesta etapa. Os alunos podem fazer seus registros escritos em folha de papel ou usando o Google Formulários, caso seja possível. É importante que o professor insira questões que façam os alunos refletirem sobre a proposta.
Discussão das soluções
O professor pode usar das respostas enviadas pelos alunos para organizar um painel de soluções a partir do Google Apresentações, disponibilizando o link para a turma ter acesso ao material. Em seguida, uma segunda etapa de questões, agora sobre as soluções apresentadas, que façam com que a turma reflita sobre as estratégias utilizadas (atenção aqui para as orientações ao professor e as problematizações propostas neste campo do plano de aula).
Sistematização
Não há.
Encerramento
Proponha aos alunos que façam, junto com a família, papéis de mesmo tamanho que contenham a mesma quantidade de bombons indicadas na Atividade Principal. Isso pode ser colocado em uma caixinha ou um saquinho, desde que não seja possível saber qual o sabor do bombom (representado pelo papel) que será retirado. Peça que os alunos, usando o Google Planilhas, façam uma tabela sobre as retiradas dos bombons, simulando as retiradas de Maria e Laura.
Caso não tenham acesso à internet, podem fazer esse movimento criando uma planilha a partir de uma folha de caderno ou uma folha quadriculada.
Raio X
Propor que os alunos respondam ao problema apresentado, seja por escrito ou usando o Google Documentos, inserindo uma explicação das estratégias utilizadas para resolução.
Convite às famílias
Convidar a família a participar, junto ao aluno, das propostas da etapa de Encerramento, seja usando recursos digitais ou não.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Cristiano Santos Rodrigues
Mentor: Edicleia Xavier da Costa
Especialista de área: Rita Batista
Habilidade da BNCC
EF04MA26 - Identificar, entre eventos aleatórios cotidianos, aqueles que têm maior chance de ocorrência, reconhecendo características de resultados mais prováveis, sem utilizar frações.
Objetivo específico
Compreender melhor a análise de eventos aleatórios e trabalhar com as possibilidades de um espaço amostral.
Conceito-chave
Aleatoriedade
Recursos necessários
- Papel
- Lápis
- Borracha
- Lousa
- Atividades projetadas em formato de slides ou impressas.











