Atividade principal
Plano de Aula
Plano de aula: Cálculos convencionais para a operação da adição
Plano 7 de uma sequência de 10 planos. Veja todos os planos sobre Estratégias convencionais e não convencionais de cálculos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Bruna Albieri Cruz da Silva
Mentora: Eliane Zanin
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF03MA05) Desenvolvimento de estratégias pessoais e convencionais de cálculo envolvendo adição, subtração e multiplicação (usando propriedades do sistema de numeração).
Conhecimentos prévios que a turma deve dominar
- Reconhecer as propriedades do sistema de numeração decimal.
- Reconhecer os numerais e quantidades.
- Possuir noções a respeito do conceito de adição.
Objetivos específicos
Realizar cálculos de adição utilizando o algoritmo convencional
Conceito-chave
Algoritmo da adição.
Recursos necessários
- Lápis.
- Papel.
- Atividades impressas.
- Ábaco e argolas coloridas (opcional).
Habilidades BNCC:
Objetivos de aprendizagem
Realizar cálculos de adição utilizando o algoritmo convencional
Resumo da aula
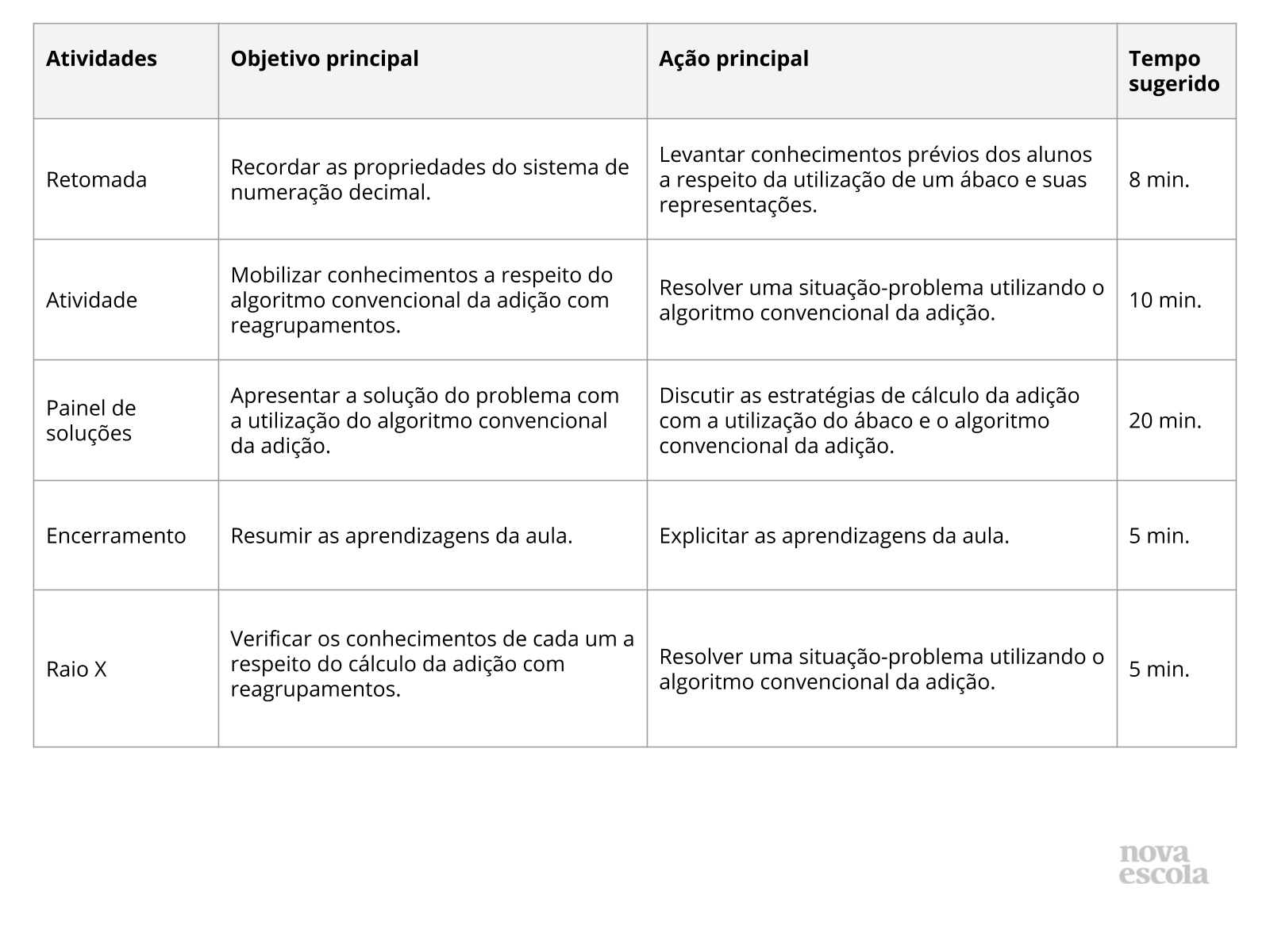 Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
Tempo sugerido: 8 minutos.
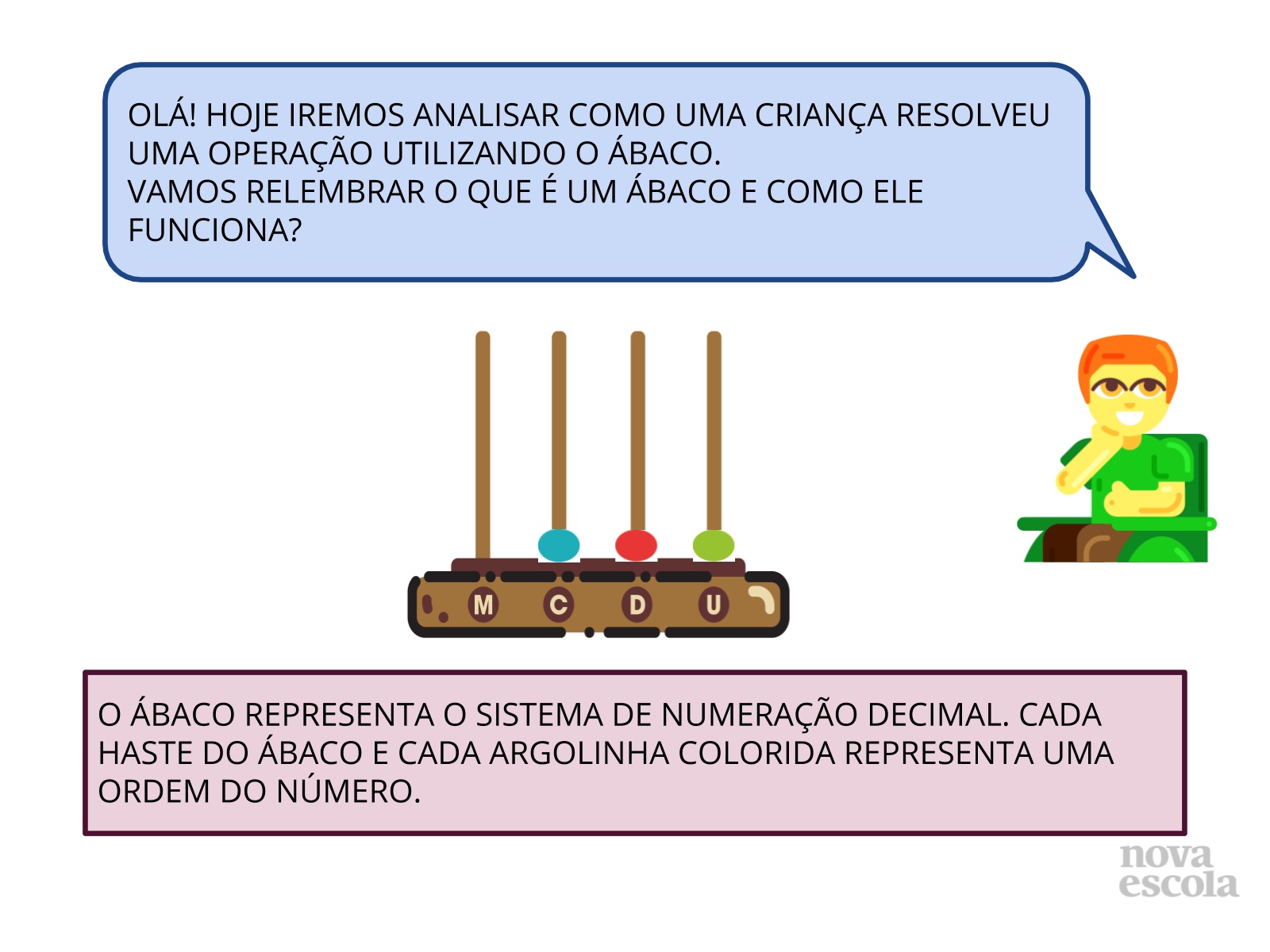
Orientações: Retome com os alunos como representar as propriedades do sistema de numeração decimal em um ábaco. O que representam as hastes e as argolinhas, assim como o valor posicional dos numerais.
Propósito: Recordar com os alunos as propriedades do sistema de numeração decimal e as representações de um ábaco.
Discuta com a turma:
- Vocês já viram um ábaco como esse?
- O que representam estas hastes?
- Para o que vocês pensam que ele serve?
- Como representar numerais com o ábaco?
Atividade principal (slides de 4 a 7)
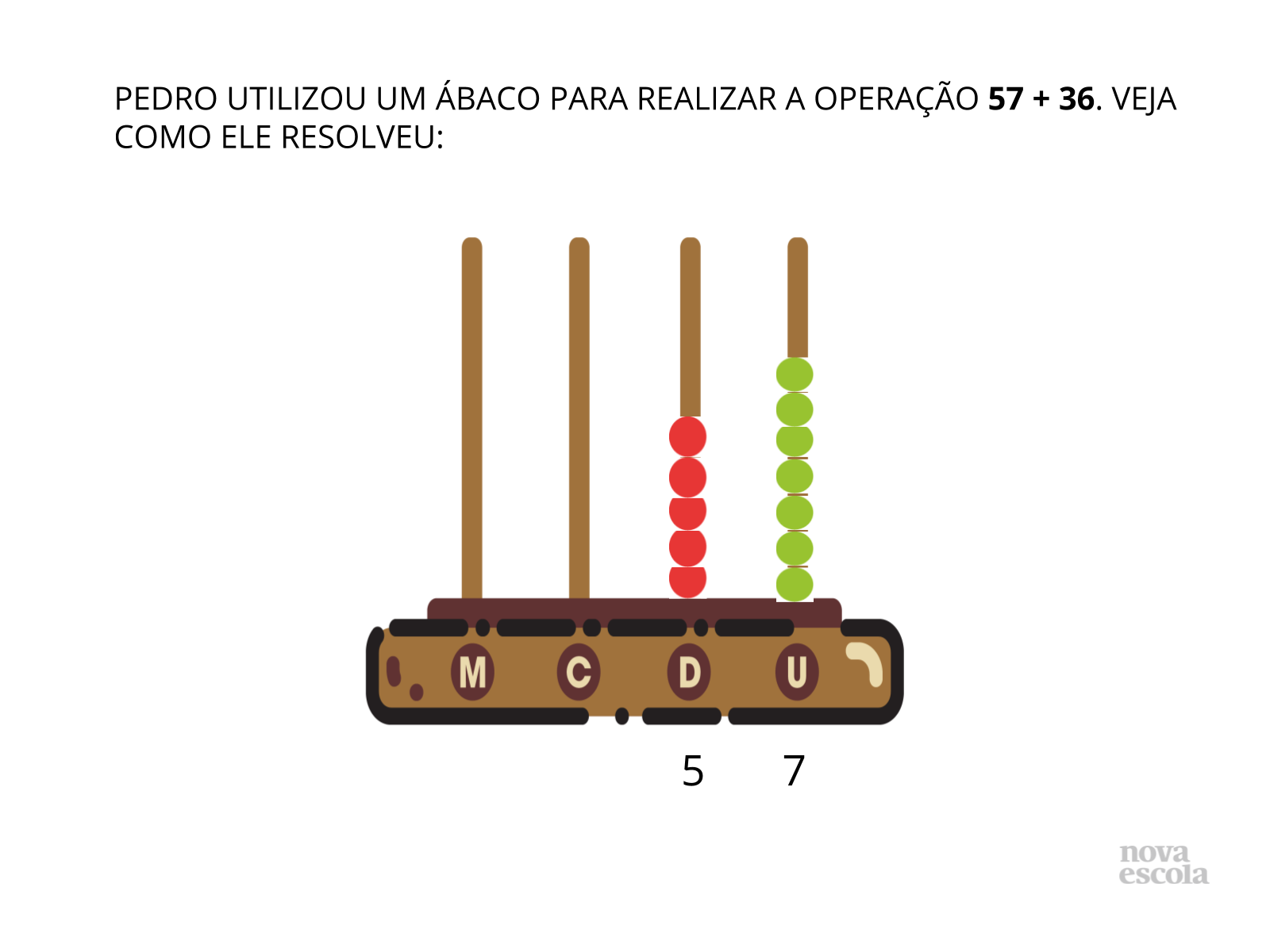
Tempo sugerido: 10 minutos.
Orientação: Introduza a atividade e peça para que os alunos reflitam sobre a forma como a resolução da operação é apresentada com a utilização do ábaco. Faça o levantamento das respostas procurando compreender qual a primeira impressão dos alunos em relação à situação posta.
Você pode demonstrar a atividade com o ábaco, ou somente apresentando as ilustrações.
Para responderem as questões, peça para que considerem os conhecimentos que já possuem sobre o conceito da adição com reagrupamentos e as propriedades do sistema de numeração decimal. No primeiro momento, eles devem responder individualmente e, em seguida, permita que socializem suas respostas com um colega. Neste momento, é interessante que caminhe pela sala e observe como os alunos estão respondendo as questões, procurando compreender o pensamento do aluno, suas hipóteses, dúvidas e fazendo questionamentos.
Propósito: Fazer com que os alunos levantem hipóteses e resolvam o problema utilizando o conceito da adição com reagrupamentos e o algoritmo convencional.
Discuta com a turma:
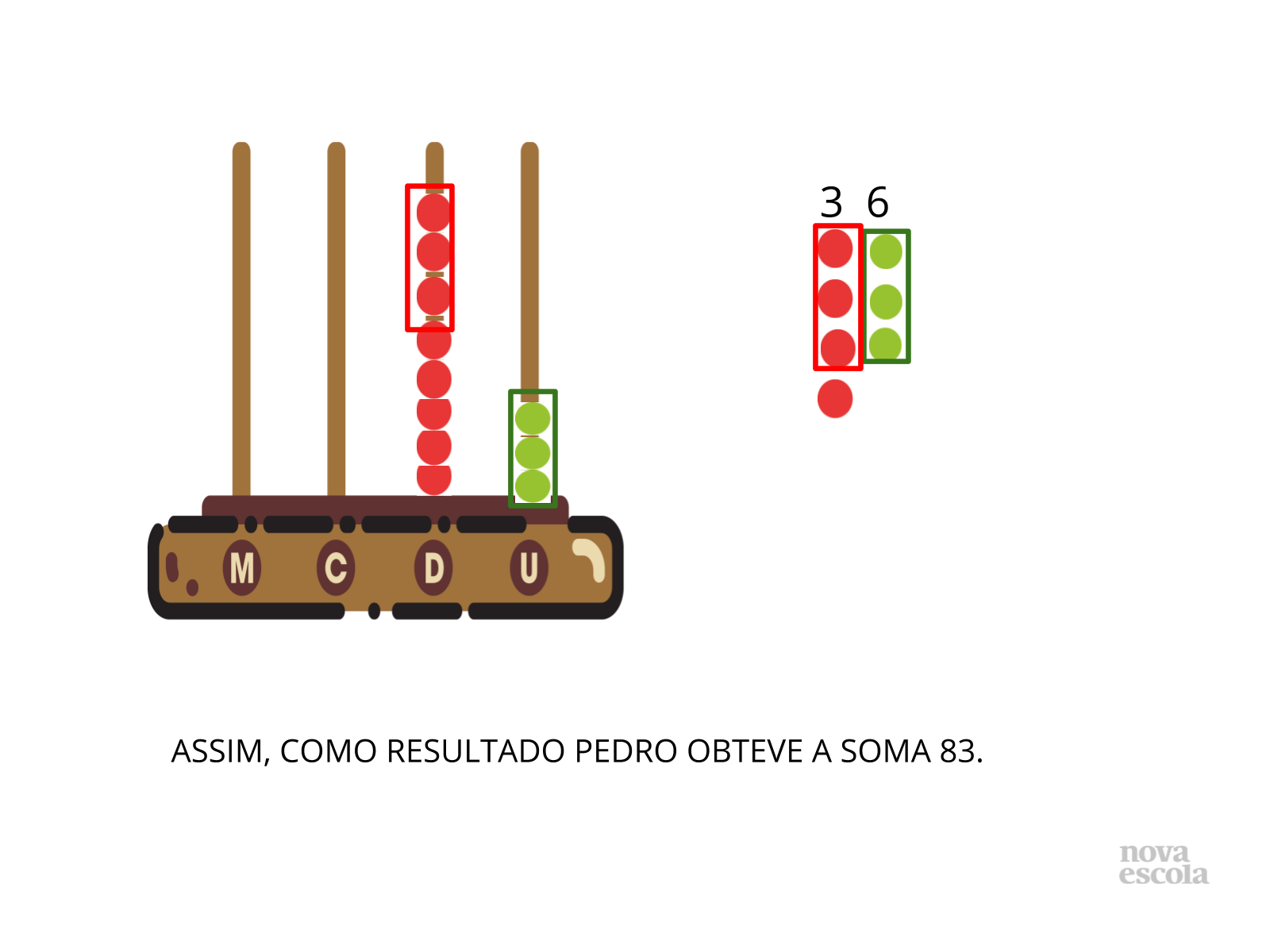
- Observe como Pedro realizou a operação.
- Como ele compôs os numerais no ábaco?
- Como o ábaco o ajudou na resolução da operação?
- Pedro possuía apenas 10 argolinhas que representam as unidades. O que ele fez para conseguir realizar a adição?
- Qual foi a estratégia utilizada por Pedro?
Materiais Complementares:
Atividade principal (slides de 4 a 7)
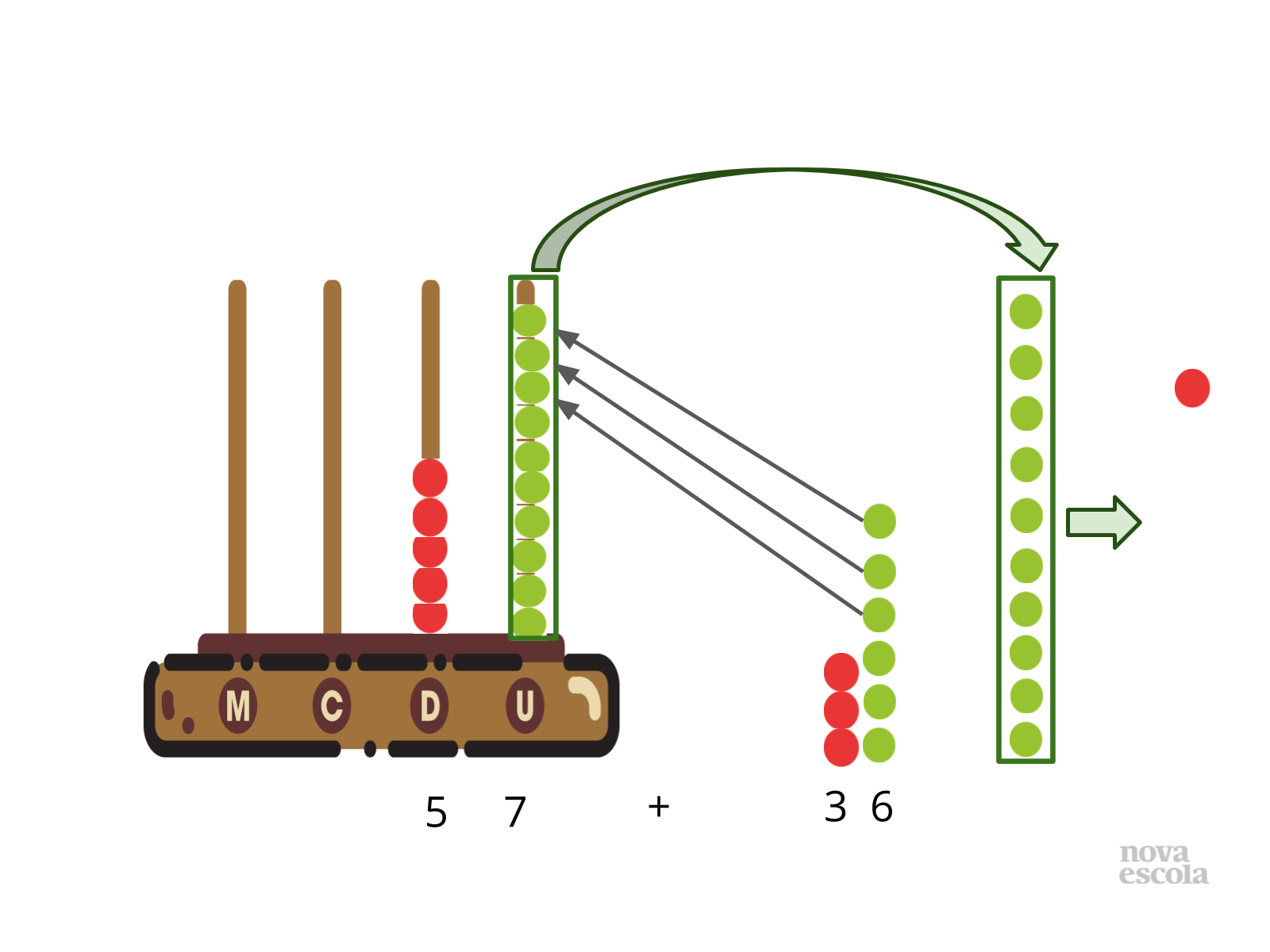
Tempo sugerido: 10 minutos.
Orientação: Introduza a atividade e peça para que os alunos reflitam sobre a forma como a resolução da operação é apresentada com a utilização do ábaco. Faça o levantamento das respostas procurando compreender qual a primeira impressão dos alunos em relação à situação posta.
Você pode demonstrar a atividade com o ábaco, ou somente apresentando as ilustrações.
Para responderem as questões, peça para que considerem os conhecimentos que já possuem sobre o conceito da adição com reagrupamentos e as propriedades do sistema de numeração decimal. No primeiro momento, eles devem responder individualmente e, em seguida, permita que socializem suas respostas com um colega. Neste momento, é interessante que caminhe pela sala e observe como os alunos estão respondendo as questões, procurando compreender o pensamento do aluno, suas hipóteses, dúvidas e fazendo questionamentos.
Propósito: Fazer com que os alunos levantem hipóteses e resolvam o problema utilizando o conceito da adição com reagrupamentos e o algoritmo convencional.
Discuta com a turma:
- Observe como Pedro realizou a operação.
- Como ele compôs os numerais no ábaco?
- Como o ábaco o ajudou na resolução da operação?
- Pedro possuía apenas 10 argolinhas que representam as unidades. O que ele fez para conseguir realizar a adição?
- Qual foi a estratégia utilizada por Pedro?
Atividade principal (slides de 4 a 7)
Tempo sugerido: 10 minutos.
Orientação: Introduza a atividade e peça para que os alunos reflitam sobre a forma como a resolução da operação é apresentada com a utilização do ábaco. Faça o levantamento das respostas procurando compreender qual a primeira impressão dos alunos em relação à situação posta.
Você pode demonstrar a atividade com o ábaco, ou somente apresentando as ilustrações.
Para responderem as questões, peça para que considerem os conhecimentos que já possuem sobre o conceito da adição com reagrupamentos e as propriedades do sistema de numeração decimal. No primeiro momento, eles devem responder individualmente e, em seguida, permita que socializem suas respostas com um colega. Neste momento, é interessante que caminhe pela sala e observe como os alunos estão respondendo as questões, procurando compreender o pensamento do aluno, suas hipóteses, dúvidas e fazendo questionamentos.
Propósito: Fazer com que os alunos levantem hipóteses e resolvam o problema utilizando o conceito da adição com reagrupamentos e o algoritmo convencional.
Discuta com a turma:
- Observe como Pedro realizou a operação.
- Como ele compôs os numerais no ábaco?
- Como o ábaco o ajudou na resolução da operação?
- Pedro possuía apenas 10 argolinhas que representam as unidades. O que ele fez para conseguir realizar a adição?
- Qual foi a estratégia utilizada por Pedro?
Atividade principal (slides de 4 a 7)

Tempo sugerido: 10 minutos.
Orientação: Introduza a atividade e peça para que os alunos reflitam sobre a forma como a resolução da operação é apresentada com a utilização do ábaco. Faça o levantamento das respostas procurando compreender qual a primeira impressão dos alunos em relação à situação posta.
Você pode demonstrar a atividade com o ábaco, ou somente apresentando as ilustrações.
Para responderem as questões, peça para que considerem os conhecimentos que já possuem sobre o conceito da adição com reagrupamentos e as propriedades do sistema de numeração decimal. No primeiro momento, eles devem responder individualmente e, em seguida, permita que socializem suas respostas com um colega. Neste momento, é interessante que caminhe pela sala e observe como os alunos estão respondendo as questões, procurando compreender o pensamento do aluno, suas hipóteses, dúvidas e fazendo questionamentos.
Propósito: Fazer com que os alunos levantem hipóteses e resolvam o problema utilizando o conceito da adição com reagrupamentos e o algoritmo convencional.
Discuta com a turma:
- Observe como Pedro realizou a operação.
- Como ele compôs os numerais no ábaco?
- Como o ábaco o ajudou na resolução da operação?
- Pedro possuía apenas 10 argolinhas que representam as unidades. O que ele fez para conseguir realizar a adição?
- Qual foi a estratégia utilizada por Pedro?
Painel de soluções (Slides de 8 a 10)

Tempo sugerido: 20 minutos.
Orientação: Convide alguns alunos para que demonstrem para o restante da sala, como resolveram a operação utilizando o algoritmo convencional. Caso haja respostas diferentes, convide estes alunos para que demonstrem a forma como pensaram a resolução da operação e permita que a turma chegue a um consenso sobre a resposta correta.
É esperado que os alunos percebam que na situação apresentada, Pedro não considerou a dezena obtida com a troca das unidades na adição da ordem das dezenas.
Propósito: Compartilhar as resoluções dos alunos e compreender a forma como pensaram.
Discuta com a turma:
- Alguém pensou de outra forma?
- Vocês acham que haveria outra forma de compor os números da operação?
- Haveria outra forma de solucionar essa operação?
- Por onde devemos começar?
- Qual a diferença entre o resultado obtido pela turma e o resultado obtido por Pedro?
- Qual foi o erro que ele cometeu?
Após as apresentações dos alunos e as discussões com a turma, retome o que já foi exposto pelos alunos e sistematize a resolução.
Painel de soluções (Slides de 8 a 10)
Tempo sugerido: 20 minutos.
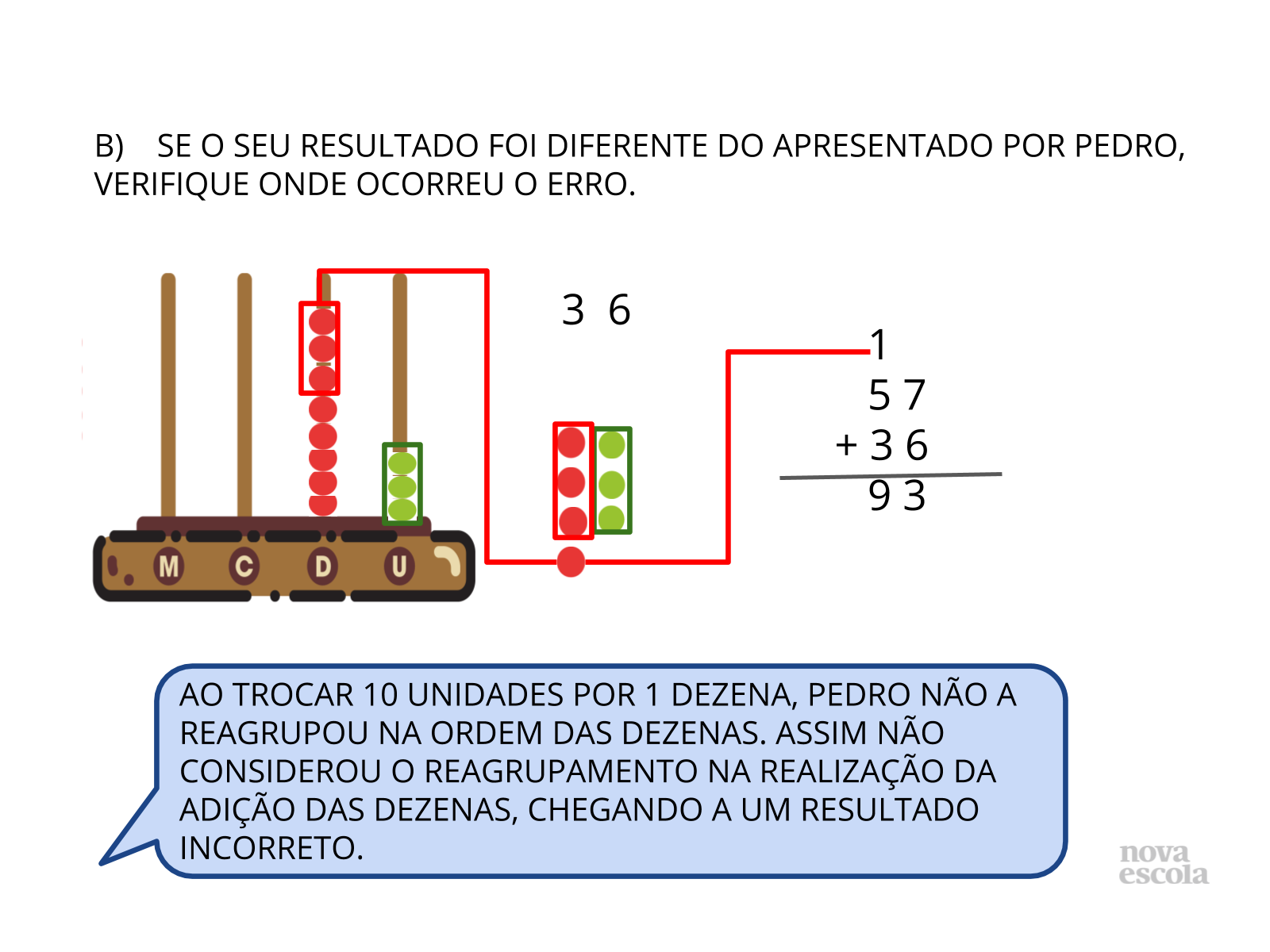
Orientação: Convide alguns alunos para que demonstrem para o restante da sala, como resolveram a operação utilizando o algoritmo convencional. Caso haja respostas diferentes, convide estes alunos para que demonstrem a forma como pensaram a resolução da operação e permita que a turma chegue a um consenso sobre a resposta correta.
É esperado que os alunos percebam que na situação apresentada, Pedro não considerou a dezena obtida com a troca das unidades na adição da ordem das dezenas.
Propósito: Compartilhar as resoluções dos alunos e compreender a forma como pensaram.
Discuta com a turma:
- Alguém pensou de outra forma?
- Vocês acham que haveria outra forma de compor os números da operação?
- Haveria outra forma de solucionar essa operação?
- Por onde devemos começar?
- Qual a diferença entre o resultado obtido pela turma e o resultado obtido por Pedro?
- Qual foi o erro que ele cometeu?
Após as apresentações dos alunos e as discussões com a turma, retome o que já foi exposto pelos alunos e sistematize a resolução.
Painel de soluções (Slides de 8 a 10)
Tempo sugerido: 20 minutos.
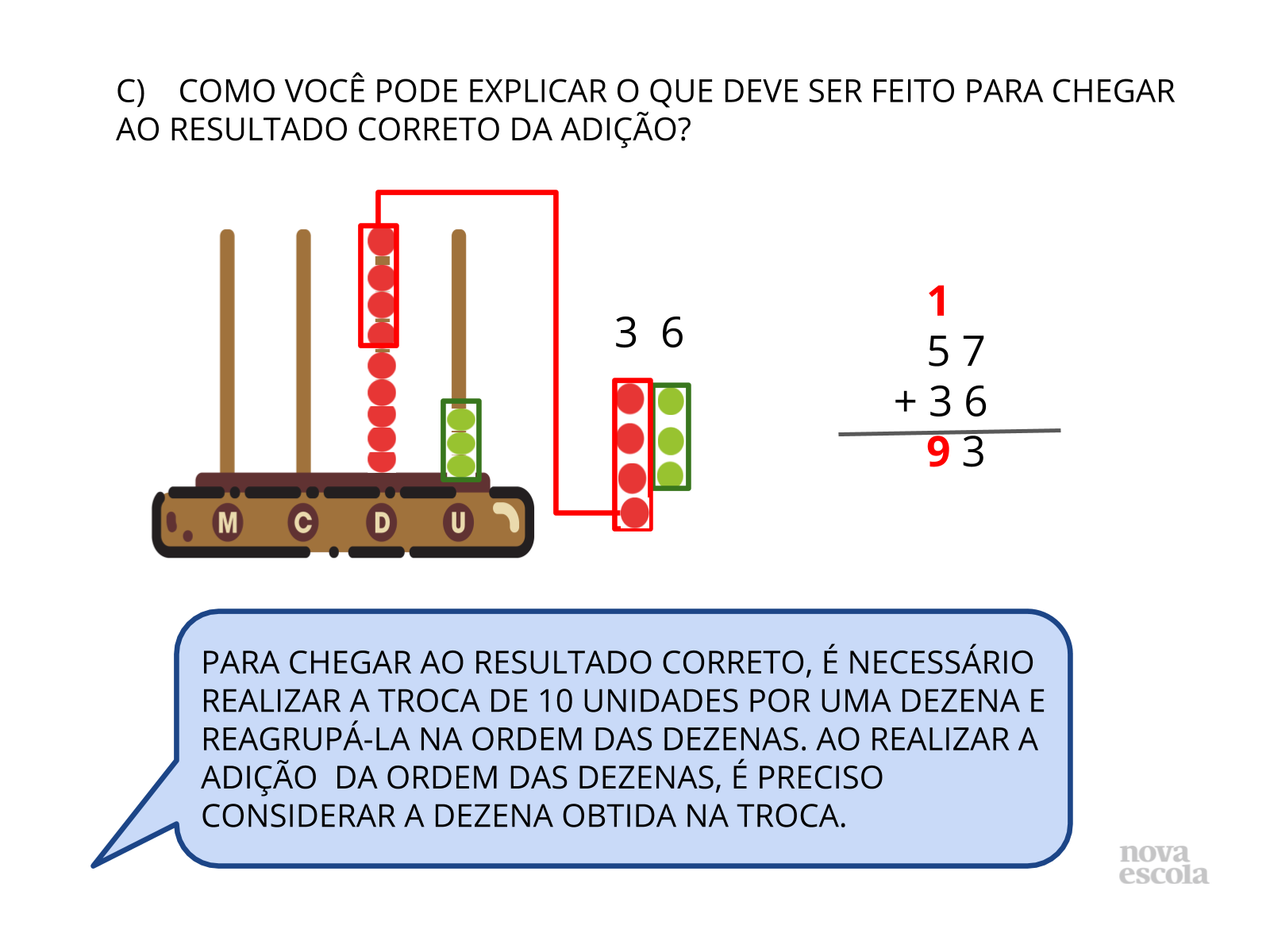
Orientação: Convide alguns alunos para que demonstrem para o restante da sala, como resolveram a operação utilizando o algoritmo convencional. Caso haja respostas diferentes, convide estes alunos para que demonstrem a forma como pensaram a resolução da operação e permita que a turma chegue a um consenso sobre a resposta correta.
É esperado que os alunos percebam que na situação apresentada, Pedro não considerou a dezena obtida com a troca das unidades na adição da ordem das dezenas.
Propósito: Compartilhar as resoluções dos alunos e compreender a forma como pensaram.
Discuta com a turma:
- Alguém pensou de outra forma?
- Vocês acham que haveria outra forma de compor os números da operação?
- Haveria outra forma de solucionar essa operação?
- Por onde devemos começar?
- Qual a diferença entre o resultado obtido pela turma e o resultado obtido por Pedro?
- Qual foi o erro que ele cometeu?
Após as apresentações dos alunos e as discussões com a turma, retome o que já foi exposto pelos alunos e sistematize a resolução..
Encerramento

Tempo sugerido: 5 minutos.
Orientação: Encerre a atividade chamando a atenção dos alunos para a utilização correta dos reagrupamentos durante a realização das operações com o algoritmo convencional.
Propósito: Resumir as aprendizagens da aula.
Raio X

Tempo sugerido: 5 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem, utilizando as estratégias discutidas na aula. Circule para verificar como os alunos estão realizando os cálculos. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções no quadro.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito do algoritmo convencional da adição.
Materiais Complementares:
Sugestão de adaptação para ensino remoto
Código do plano
MAT3_04NUM07
Recursos
- Necessários: estojo, papel ou caderno do aluno para que faça as anotações pertinentes.
Algum meio de comunicação com alunos: Zoom, Meet, WhatsApp, e-mail ou impressão.
Atividade principal.
Ábaco, ábaco desenhado ou ábaco virtual
- Opcionais:
Celular, computador ou tablet
Ábaco virtual
Vídeo: Adição com o ábaco
Vídeo: Ábaco
Para este plano, foque na etapa da Atividade principal
Atividade principal
O foco desta atividade principal é realizar cálculos de adição utilizando o algoritmo convencional. Para a realização da atividade, os alunos precisam ter acesso aos slides que mostram a atividade principal. Se estiver em uma videoconferência, apresente os slides com a situação problema. Caso esteja em uma aula assíncrona/síncrona por WhatsApp ou ferramenta semelhante, envie as imagens dos slides em forma de fotografia (print) ou o arquivo da atividade principal. Primeiramente, os slides irão mostrar como a operação de adição é realizada no ábaco. Depois, você pode apresentar a atividade que os alunos deverão realizar em forma de texto ou áudio. Os alunos devem copiá-la no caderno. De todas as formas os alunos devem copiar a situação no caderno. Questione os alunos:
- Observe como Pedro realizou a operação.
- Como ele compôs os numerais no ábaco?
- Como o ábaco o ajudou na resolução da operação?
- Pedro possuía apenas 10 argolinhas que representam as unidades. O que ele fez para conseguir realizar a adição?
- Qual foi a estratégia utilizada por Pedro?
- Quais são as possibilidades de solução?
Primeiramente, os alunos devem tentar efetuar a operação de adição pelo algoritmo individualmente, depois podem comentar com os colegas e pedir ajuda, caso estejam encontrando alguma dificuldade.
Painel de soluções
Compartilhe ou fotografe os slides do painel de soluções e compartilhe via WhatsApp ou outro meio de interação com o aluno que você esteja utilizando. Os alunos devem apresentar também as formas que realizaram a operação por fotografias ou de forma escrita. Depois, podem observar as soluções dos slides e escrever ou enviar áudios, respondendo-as ou comentando-as. Podem também comparar com as que foram encontradas por eles e, assim, complementar o painel de soluções.
Encerramento
Conclua a aula com o slide ou com o que está escrito na sistematização do conceito para que os alunos copiem no caderno como forma de anotação para consultas posteriores. Pergunte se os alunos gostariam de complementar o registro com alguma outra informação.
Raio X
A atividade do Raio X pode ser usada como tarefa de casa ou como avaliação da aula. Envie e faça a discussão da mesma forma que fez com a atividade principal. Lembre-se também que há atividades complementares que podem ser enviadas para os alunos como atividades de fixação ou sistematização.
Convite às famílias
É interessante que os alunos envolvam as pessoas que estão ao seu redor em suas atividades escolares, mas devemos considerar que algumas vezes essas pessoas não poderão deixar seus afazeres e trabalhos para ajudá-los.
Envie uma mensagem de texto ou áudio explicando o que está sendo trabalhado em aula e pedindo a colaboração das famílias para auxiliar os alunos na organização de seus materiais.
Uma forma de envolvimento da família com os alunos nesta atividade poderia ser no uso do ábaco, incentivando que os alunos representem os números e que realizem operações pelo ábaco e pelo algoritmo convencional.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Bruna Albieri Cruz da Silva
Mentora: Eliane Zanin
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF03MA05) Desenvolvimento de estratégias pessoais e convencionais de cálculo envolvendo adição, subtração e multiplicação (usando propriedades do sistema de numeração).
Conhecimentos prévios que a turma deve dominar
- Reconhecer as propriedades do sistema de numeração decimal.
- Reconhecer os numerais e quantidades.
- Possuir noções a respeito do conceito de adição.
Objetivos específicos
Realizar cálculos de adição utilizando o algoritmo convencional
Conceito-chave
Algoritmo da adição.
Recursos necessários
- Lápis.
- Papel.
- Atividades impressas.
- Ábaco e argolas coloridas (opcional).















