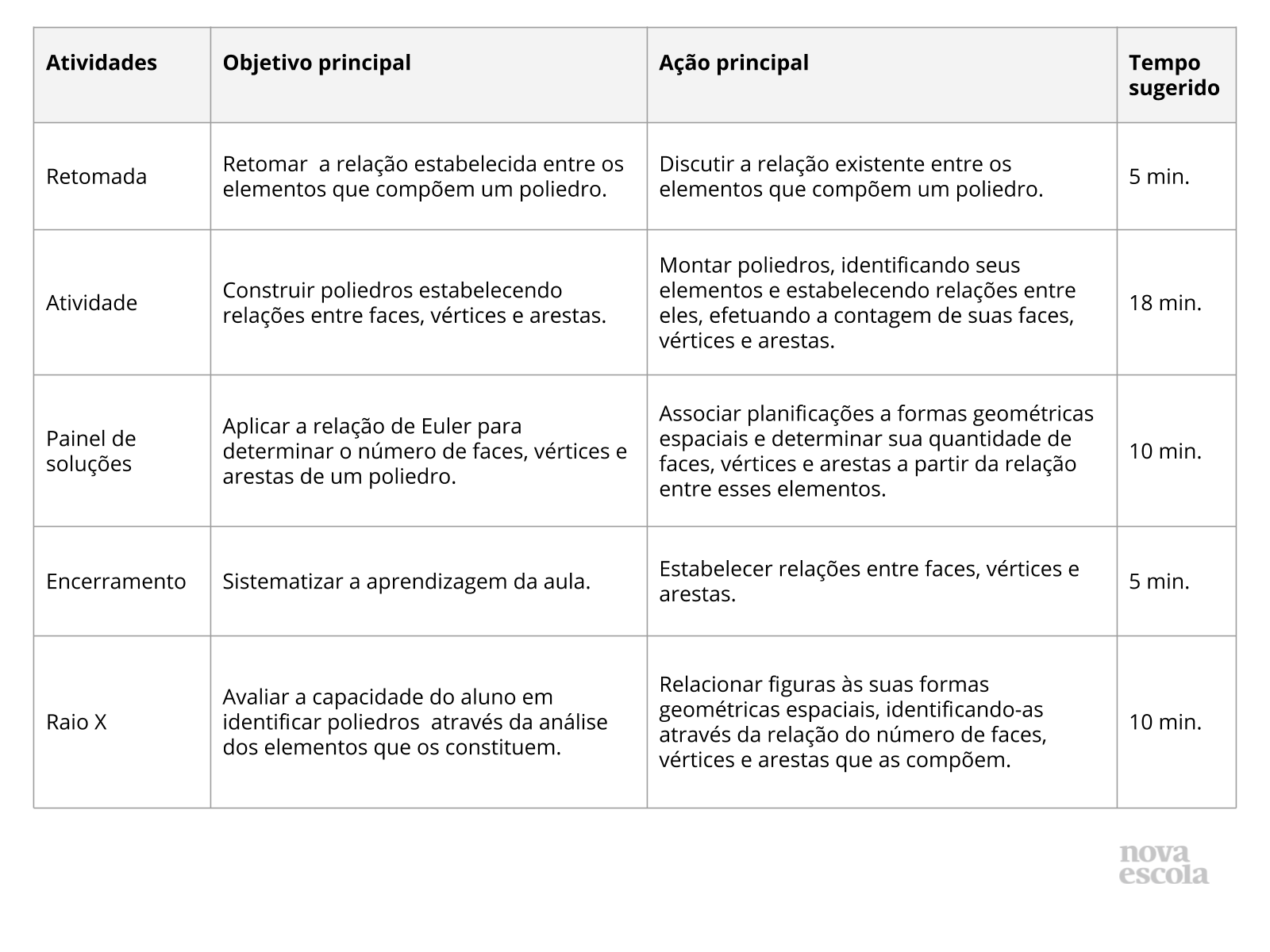
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
Tempo sugerido: 5 minutos.
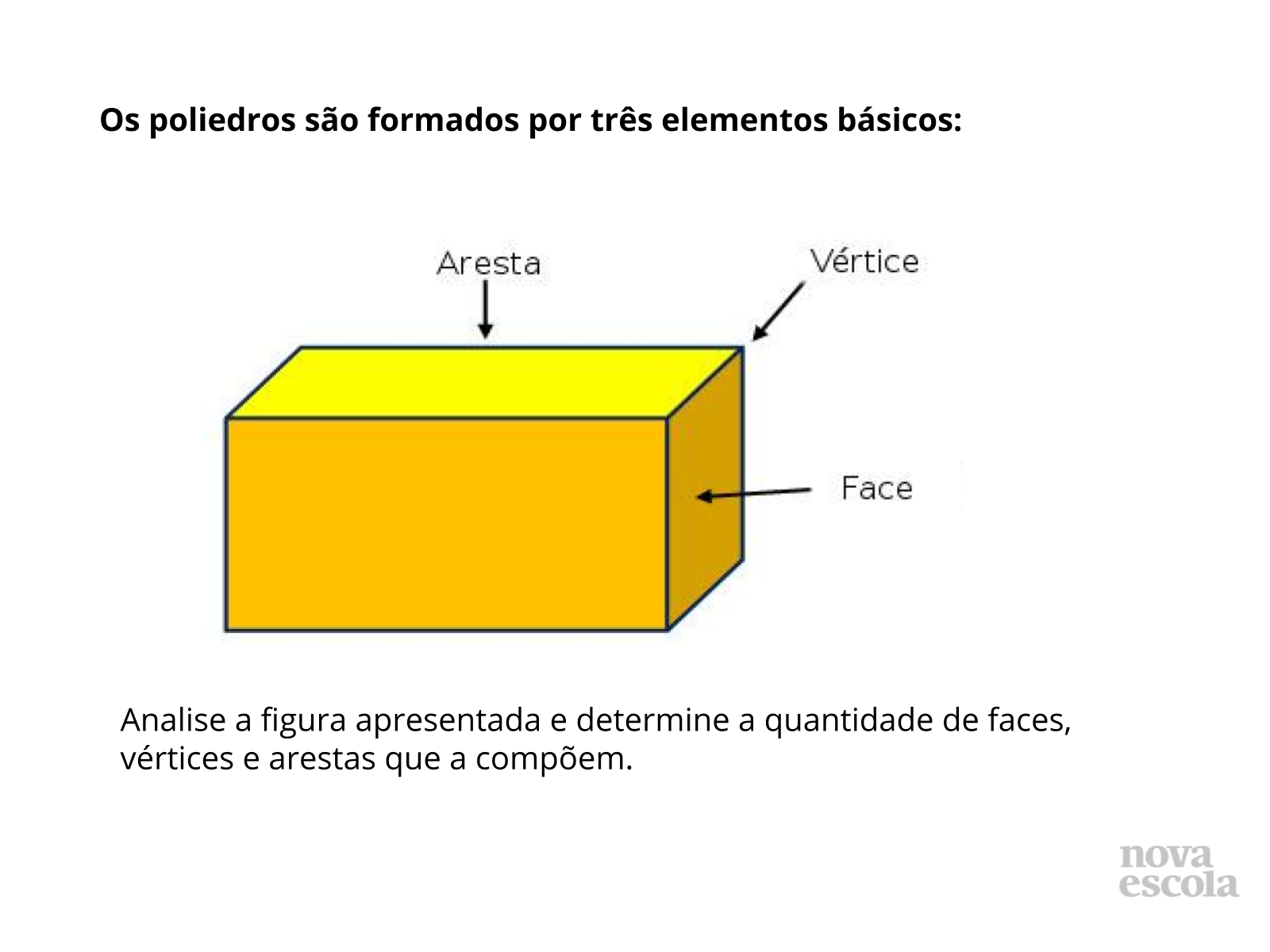
Orientação: Retome o conceito de poliedros (Figuras tridimensionais constituídas apenas por superfícies planas e composta por elementos denominados de faces, vértices e arestas).
Deixe que os alunos façam a contagem desses elementos e discuta a relação de dependência existente entre eles (Arestas - Vértices + Faces = dois: A - V + F = 2) ressaltando a importância da expressão para determinar o número de faces, vértices e arestas de qualquer poliedro.
Propósito: Retomar a relação estabelecida entre os elementos que constituem um poliedro.
Discuta com a turma:
- Para obter a quantidade de faces, vértices e arestas é necessário contar todos os elementos? (Não, aplicando a relação encontrada entre os elementos que compõem um poliedro, ao se obter a quantidade de dois de seus elementos é possível determinar o terceiro).
- Ao encontrar a quantidade de faces e arestas, como fazemos para determinar a quantidade de vértices? (Basta subtrair a quantidade de faces da quantidade de arestas e adicionar duas unidades: A - F + 2 = V)
- Se obtemos a quantidade de faces e vértices, como determinar a quantidade de arestas? (Somamos a quantidade de faces com a quantidade de vértices e subtraímos duas unidades: F + V - 2 = A)
- Dada a quantidade de vértices e arestas, como determinar a quantidade de faces? (Subtraímos a quantidade de vértices da quantidade de arestas e adicionamos duas unidades: A - V + 2 = F)
Atividade Principal
Tempo sugerido: 18 minutos
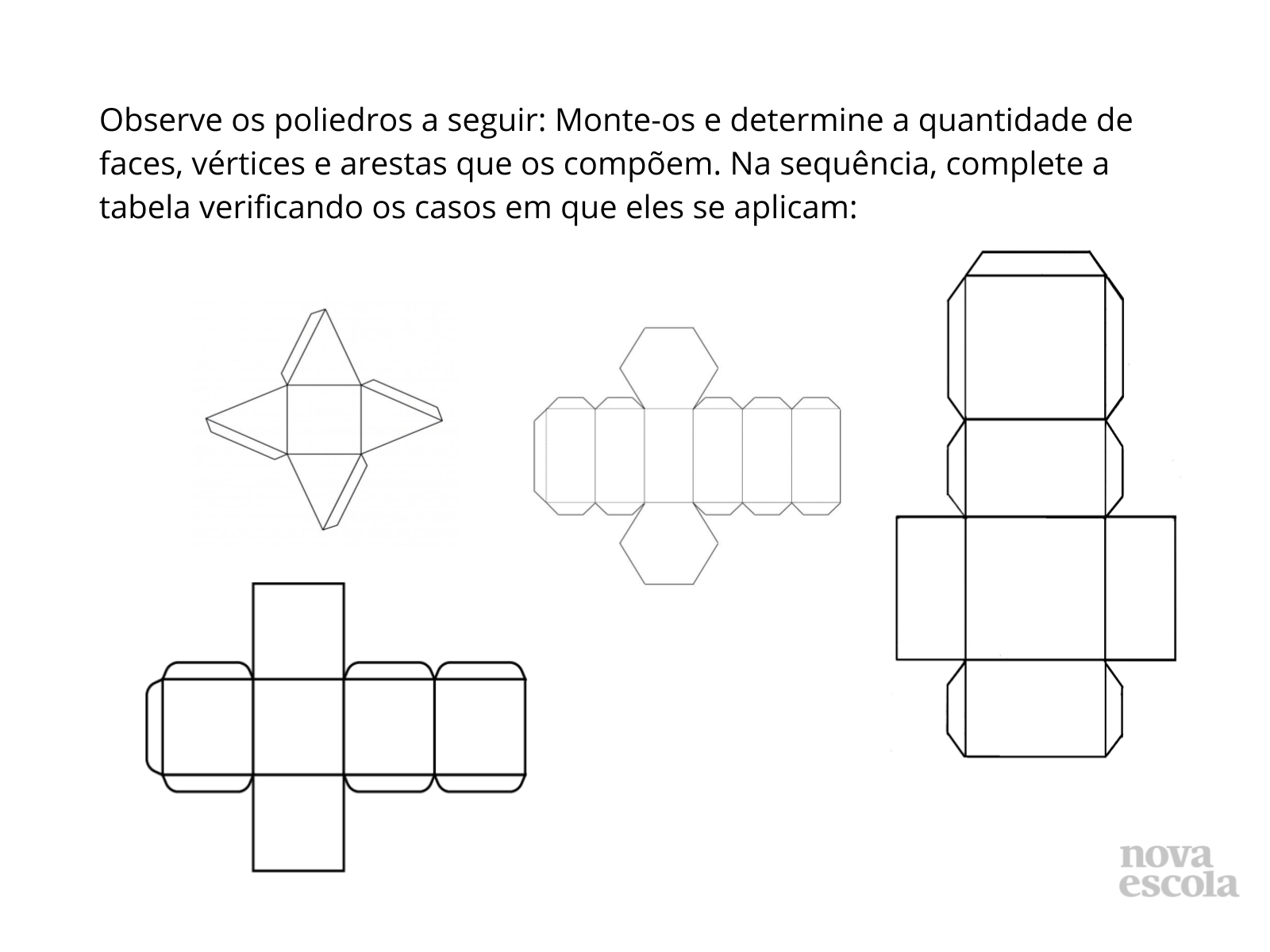
Orientações: Divida a turma em duplas, entregue os moldes das figuras para que os alunos os recortem e montem. Projete a tabela no quadro para uma ampla visualização e entregue uma cópia da tabela a cada dupla para que eles as completem após verificação do poliedro montado.
Propósito: Construir poliedros estabelecendo relações entre faces, vértices e arestas.
Discuta com a turma:
- Com quais formas são possíveis relacionar cada molde? (Os moldes apresentados representam as planificações de uma pirâmide de base quadrada, um prisma de base hexagonal, um paralelepípedo e um cubo)
- Como fazer para identificar as faces, as arestas e os vértices de cada poliedro? (As faces são cada um dos lados que compõem o poliedro, as arestas são formadas pelo encontro de faces e os vértices formado pelo encontro das arestas)
- Será necessário efetuar a contagem de cada uma das faces, vértices e arestas para obter a quantidade exata de todos os elementos que compõem o poliedro? (Não, obtendo a quantidade de dois de seus elementos é possível determinar o terceiro aplicando a relação de dependência existente eles determinadas pela expressão: V - A + F = 2)
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal

Tempo sugerido: 18 minutos
Orientações: Divida a turma em duplas, entregue os moldes das figuras para que os alunos os recortem e montem. Projete a tabela no quadro para uma ampla visualização e entregue uma cópia da tabela a cada dupla para que eles as completem após verificação do poliedro montado.
Propósito: Construir poliedros estabelecendo relações entre faces, vértices e arestas.
Discuta com a turma:
- Com quais formas são possíveis relacionar cada molde? (Os moldes apresentados representam as planificações de uma pirâmide de base quadrada, um prisma de base hexagonal, um paralelepípedo e um cubo)
- Como fazer para identificar as faces, as arestas e os vértices de cada poliedro? ( As faces são cada um dos lados que compõem o poliedro, as arestas são formadas pelo encontro de faces e os vértices formado pelo encontro das arestas)
- Será necessário efetuar a contagem de cada uma das faces, vértices e arestas para obter a quantidade exata de todos os elementos que compõem o poliedro? ( Não, obtendo a quantidade de dois de seus elementos é possível determinar o terceiro aplicando a relação de dependência existente eles determinadas pela expressão: V - A + F = 2)
Discussão da Solução
Tempo sugerido: 10 minutos
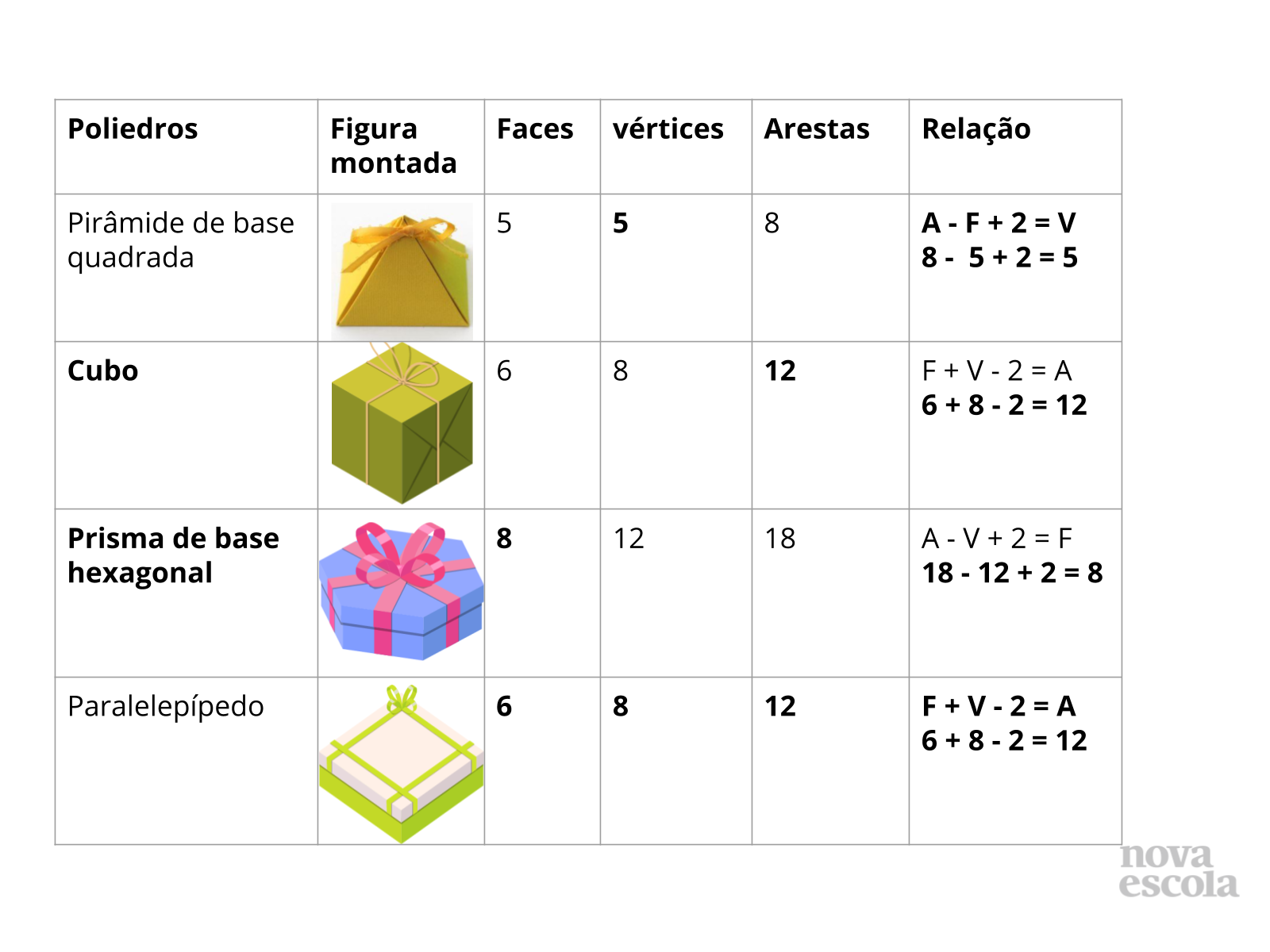
Orientações: Nesse momento é importante que o professor deixe os alunos arriscarem qual relação deve ser aplicada para determinar a quantidade de elementos que faltam para completar a tabela. Após feitas verificação e complementação dos espaços sugeridos, socialize com o grupo para saber se mais duplas chegaram ao mesmo resultado.
Propósito: Aplicar a relação de Euler para determinar o número de faces, vértices e arestas de um poliedro.
Discuta com a turma:
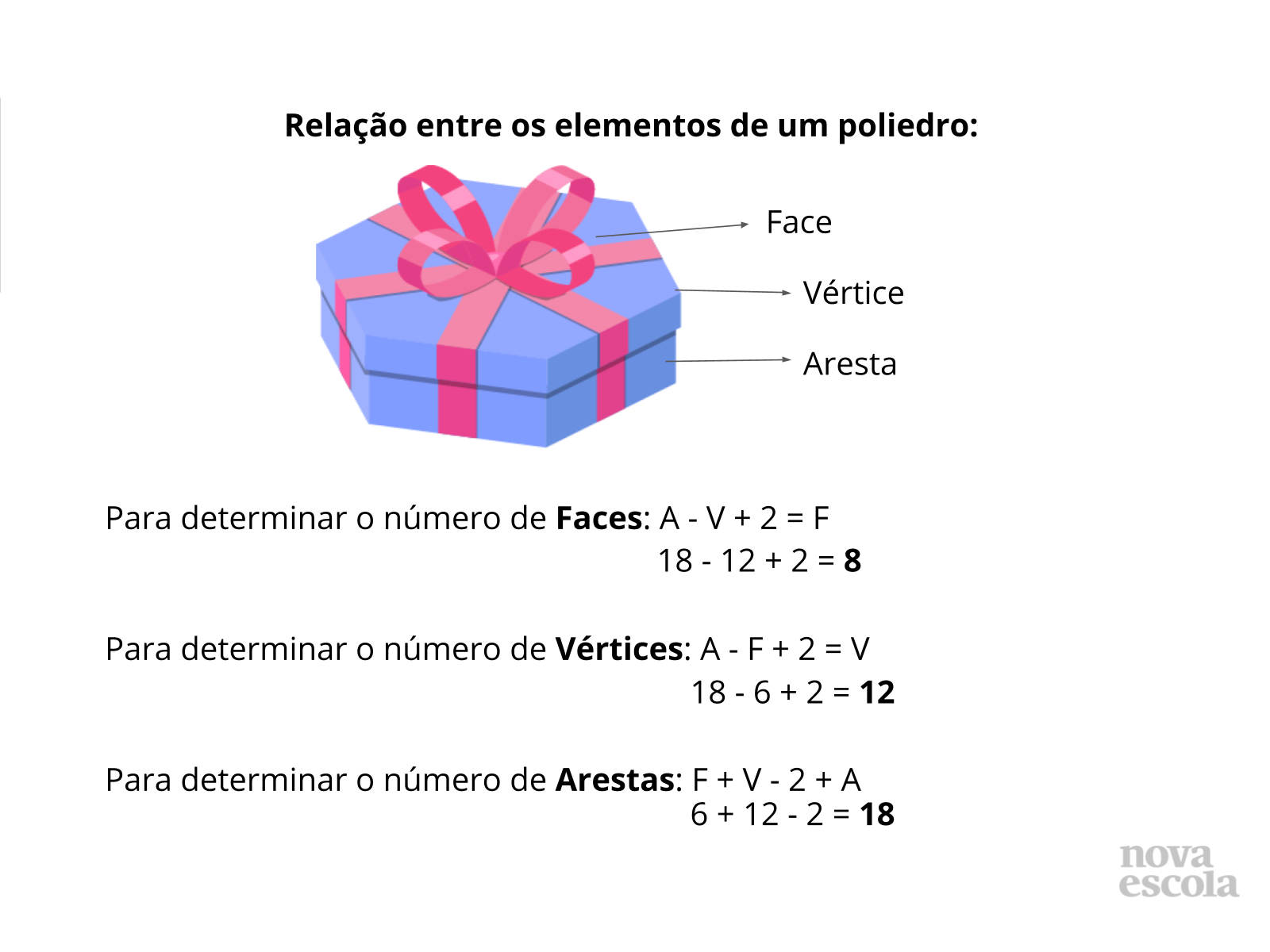
- Qual relação foi aplicada para obter a quantidade de faces? ( A - V + 2 = F)
- Qual relação foi aplicada para obter o número exato de vértices? (A - F + 2 = V)
- Qual relação foi aplicada para obter a quantidade de arestas? (F + V - 2 = A)
Encerramento
Tempo sugerido: 5 minutos
Orientações: Socialize com o grupo quais conhecimentos foram adquiridos na aula.
Propósito: Compartilhar os conhecimentos adquiridos na aula.
Discuta com a turma:
O que aprendemos hoje na aula? (Resposta pessoal)
Raio X

Tempo sugerido: 10 minutos
Orientações: Represente as figuras na lousa ou apresente caixas semelhantes às que aparecem na questão para que os alunos melhor visualizem e identifiquem as propriedades que as compõem.
Propósito: Relacionar figuras às suas formas geométricas espaciais, identificando-as através da relação do número de faces, vértices e arestas que as compõem.
Discuta com a turma:
Com qual figura espacial se assemelha cada embalagem?
Qual a quantidade de faces e vértices possui cada figura?
Ao obter a quantidade de faces e vértices, como é possível determinar a quantidade de arestas sem que seja necessário contar uma a uma?
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
Raio X

Tempo sugerido: 10 minutos
Orientações: Represente as figuras na lousa ou apresente caixas semelhantes às que aparecem na questão para que os alunos melhor visualizem e identifiquem as propriedades que as compõem.
Propósito: Relacionar figuras às suas formas geométricas espaciais, identificando-as através da relação do número de faces, vértices e arestas que as compõem.
Discuta com a turma:
Com qual figura espacial se assemelha cada embalagem?
Qual a quantidade de faces e vértices possui cada figura?
Ao obter a quantidade de faces e vértices, como é possível determinar a quantidade de arestas sem que seja necessário contar uma a uma?



















