Guia de intervenções
Plano de Aula
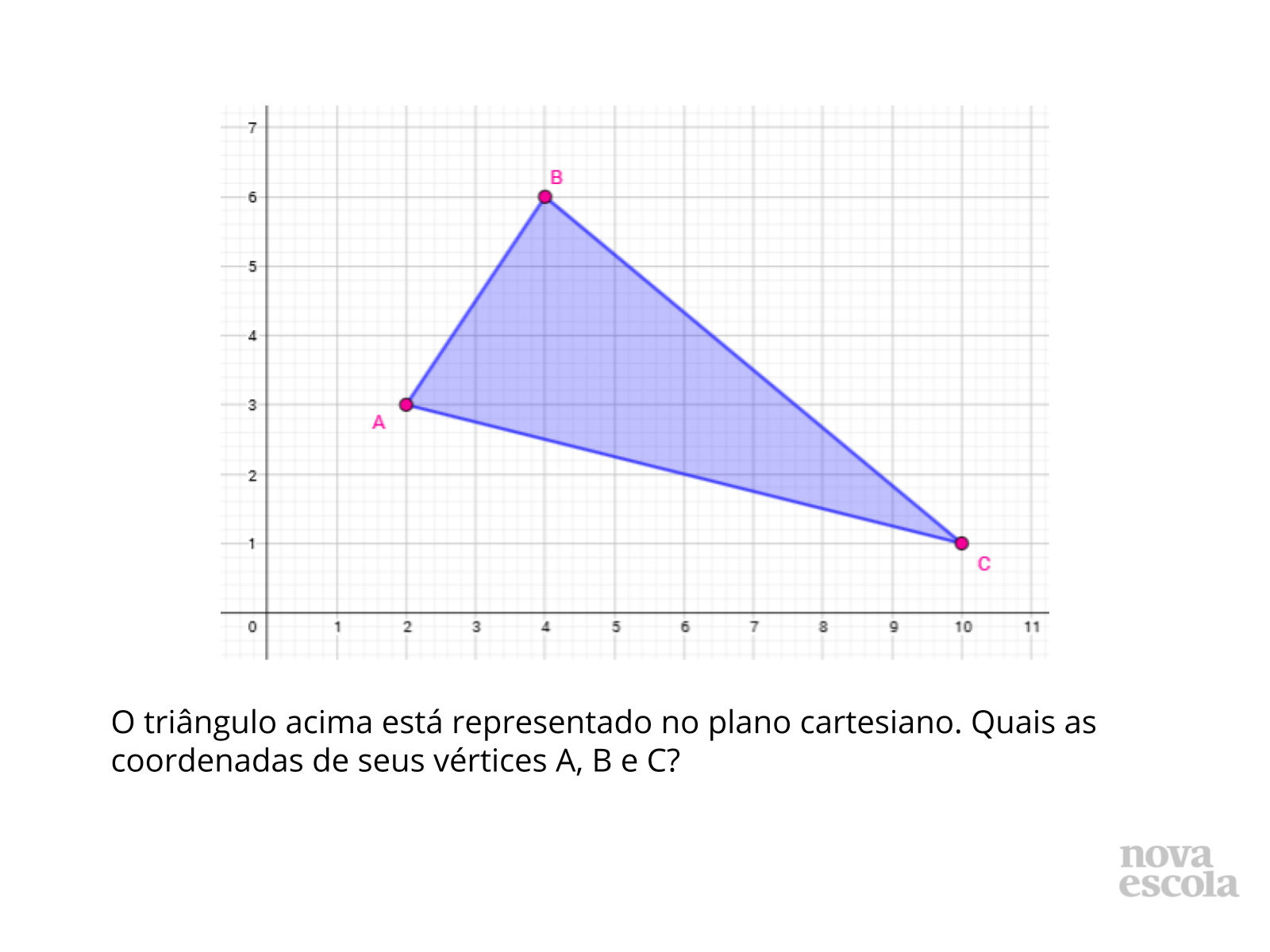
Plano de aula: Semelhanças no plano cartesiano
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Ampliação e redução de figuras planas em malhas quadriculadas
Por: Paula Vieira Soares
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Paula Vieira
Mentora: Renata S. Gonçalves
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
EF06MA20 - Construção de figuras semelhantes: ampliação e redução de figuras planas em malhas quadriculadas.
Objetivos específicos
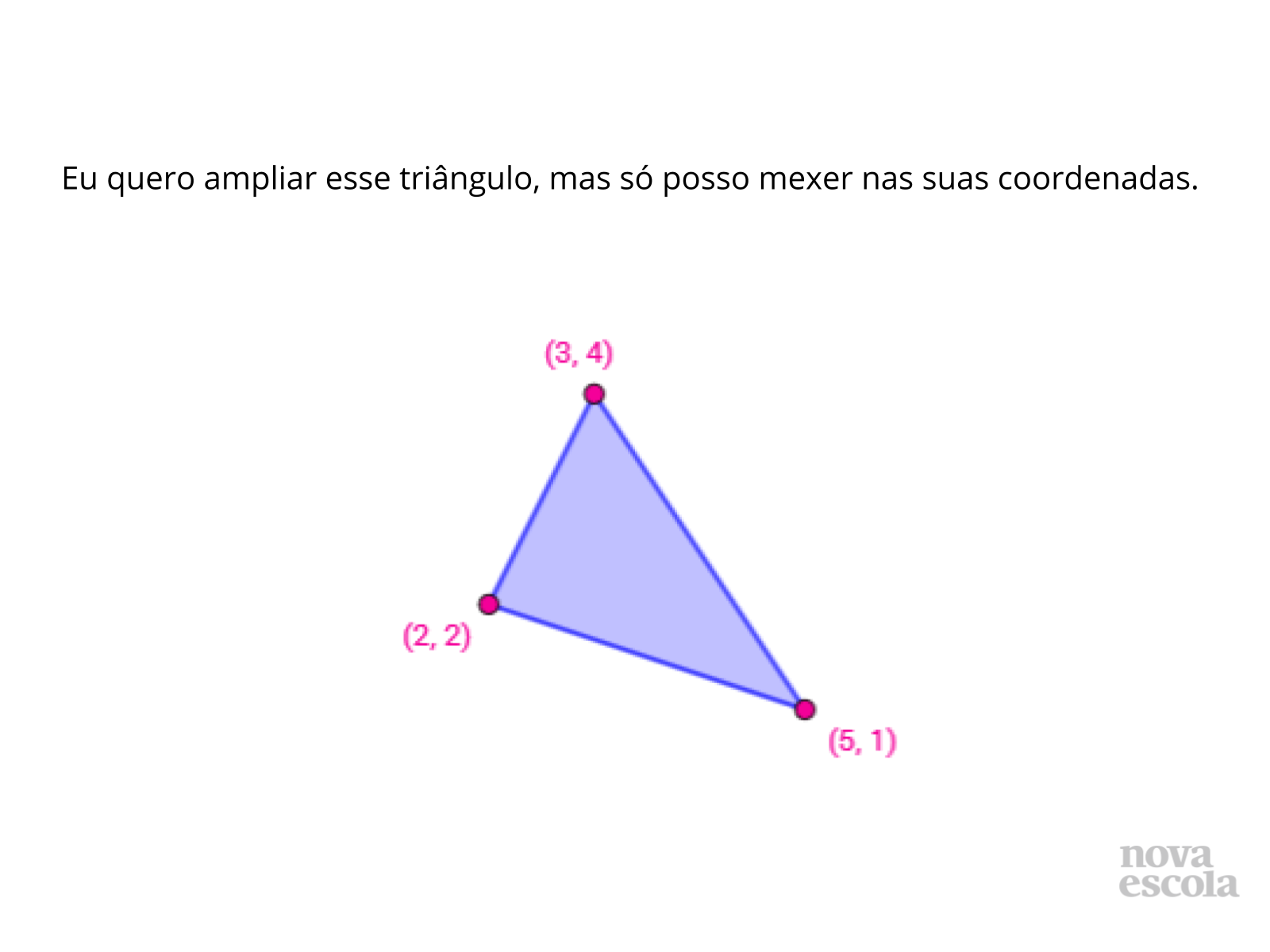
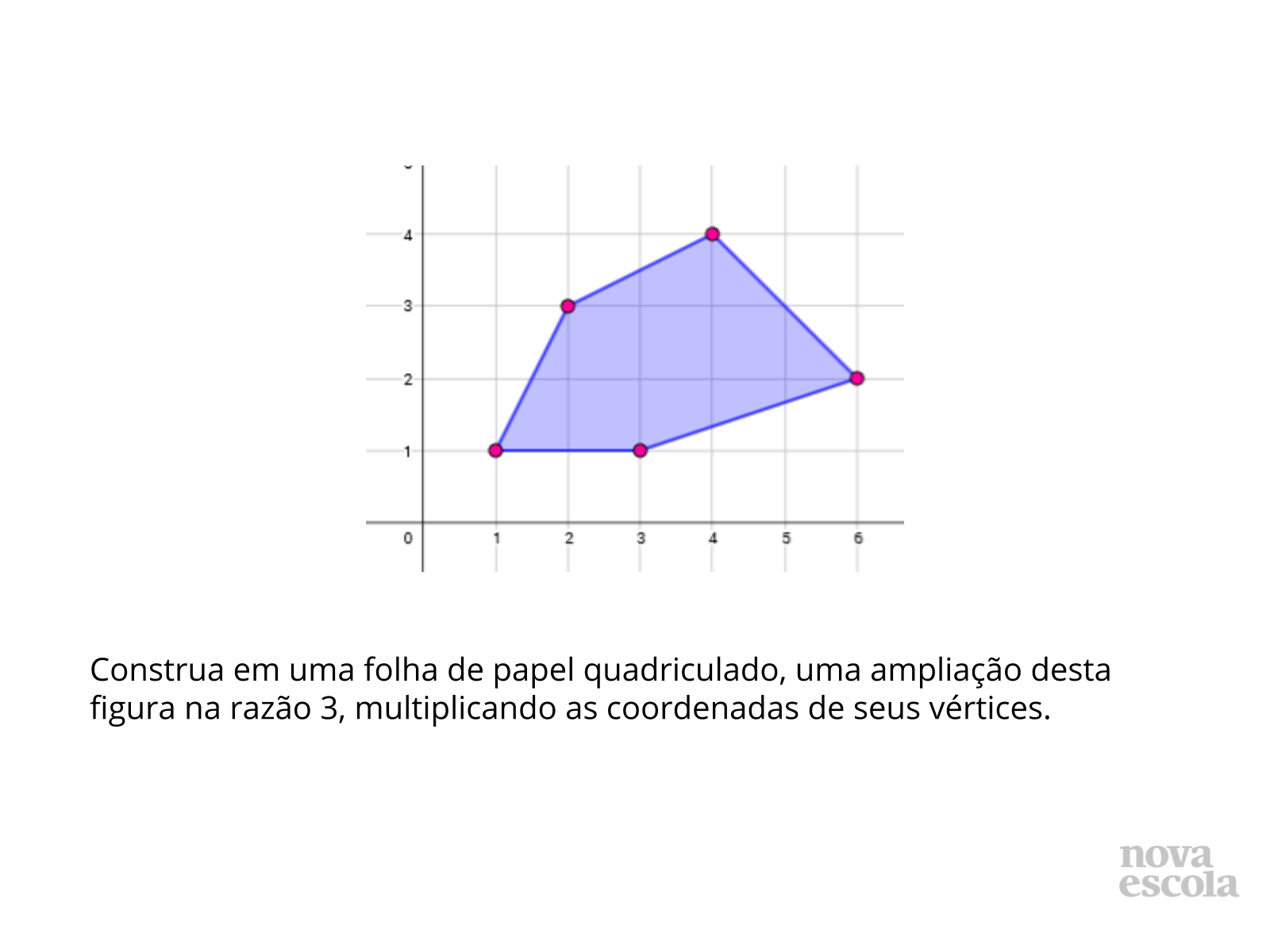
Aprofundar o estudo de semelhanças através de reduções e ampliações no plano cartesiano.
Conceito-chave
Ampliação, redução e semelhança.
Recursos necessários
- Régua;
- Papel quadriculado;
Sugestões de Leitura
MACHADO, Nílson José. Semelhança não é mera coincidência - (Coleção Vivendo a Matemática). Scipione, 2000.
SBPC - CIÊNCIA HOJE NA ESCOLA - Volume 8 - Matemática - Por que e pra que? - Brincar e aprender - Coordenadas no plano. p. 31 - RJ. Global, 1999.
BOALER, Jo. Mentalidades Matemáticas. 1ª ed. Porto Alegre - RS. Penso, 2018
Conhecimentos que a turma deve dominar:
- Plano cartesiano;
- Operações com coordenadas no plano cartesiano (multiplicação de número natural por par ordenado, adição de pares ordenados, etc.);
Habilidades BNCC:
Objetivos de aprendizagem
Aprofundar o estudo de semelhanças através de reduções e ampliações no plano cartesiano.
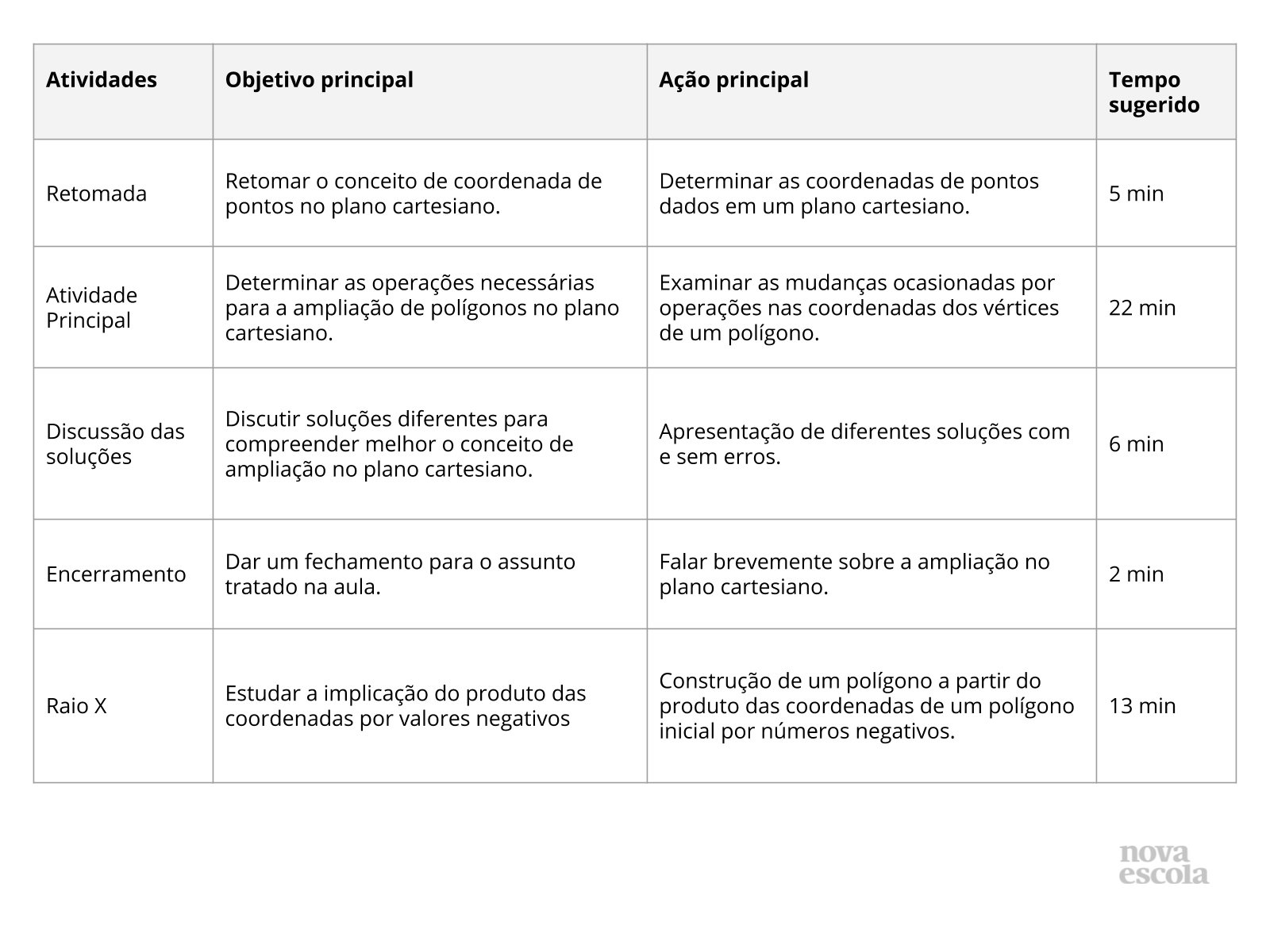 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.