Resumo da Aula
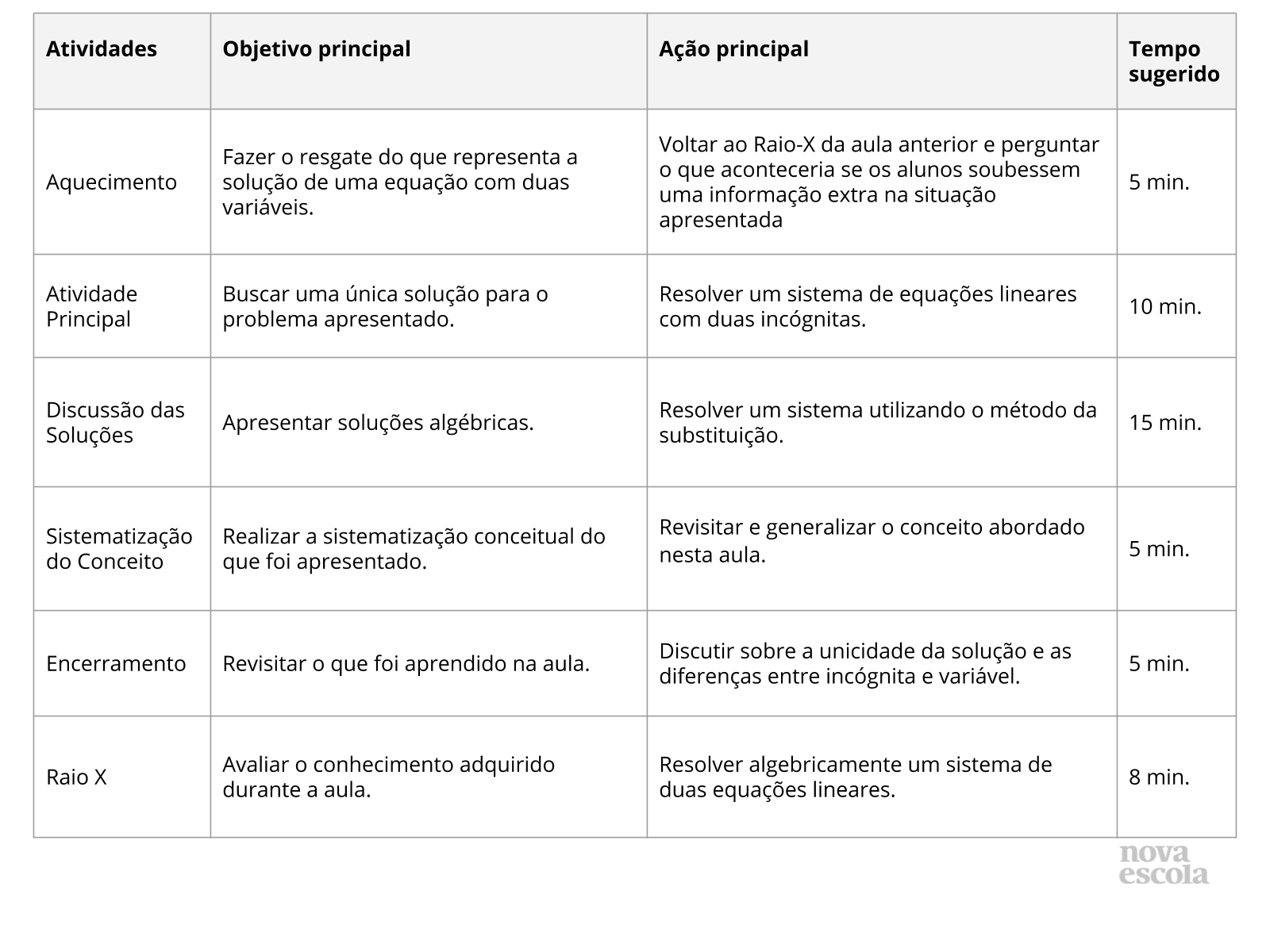
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo
Tempo sugerido: 2 minutos.
Orientação: Projete o slide ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento
Tempo sugerido: 5 minutos.
Orientações: Neste momento, retome os conhecimentos adquiridos na aula anterior.
Propósito: Revisitar os conhecimentos aprendidos na aula anterior para aplicá-los nesta aula.
Aquecimento
Tempo sugerido: 5 minutos.
Orientações: Leia a nova condição para a turma e verifique as estratégias que eles podem elaborar para responder à nova situação.
Propósito: Revisitar os conhecimentos aprendidos na aula anterior para aplicá-los nesta aula.
Aquecimento
Tempo sugerido: 5 minutos.
Orientações: Leia as duas condições, observe e compartilhe as estratégias que os alunos trazem para tentar responder à nova situação.
Propósito: Revisitar os conhecimentos aprendidos na aula anterior para aplicá-los nesta aula.
Aquecimento
Tempo sugerido: 5 minutos.
Orientações: Estimule os alunos a tentarem encontrar uma única solução para o problema proposto.
Propósito: Revisitar os conhecimentos aprendidos na aula anterior para aplicá-los nesta aula.
Atividade Principal
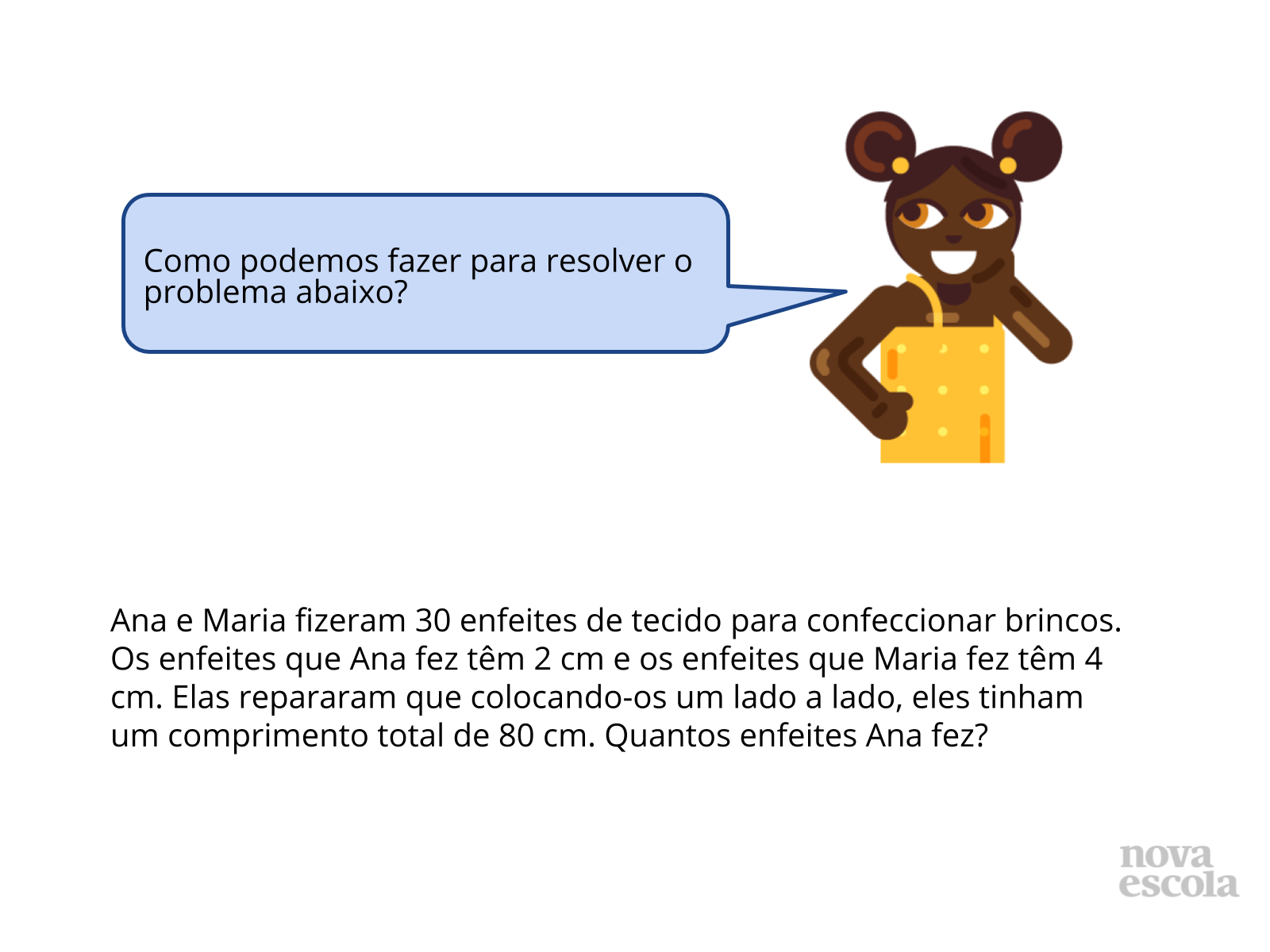
Tempo sugerido: 10 minutos.
Orientações: Neste momento, deixe os alunos procurarem todas as soluções possíveis do problema proposto. Incentive-os a pensar sozinhos e depois peça que verifiquem com o colega do lado as respostas encontradas. Peça para eles compararem as respostas encontradas. Por fim, procure que eles cheguem a uma conclusão.
Propósito: Procurar diferentes estratégias para responder ao problema proposto.
Discuta com a Turma:
- Esse problema apresenta mais de uma solução?
- Por que não há como apresentar mais do que uma solução?
- Quais as diferentes estratégias utilizadas?
Materiais Complementares:
Atividade para impressão
Resolução da atividade
Guia de intervenção
Atividade Principal
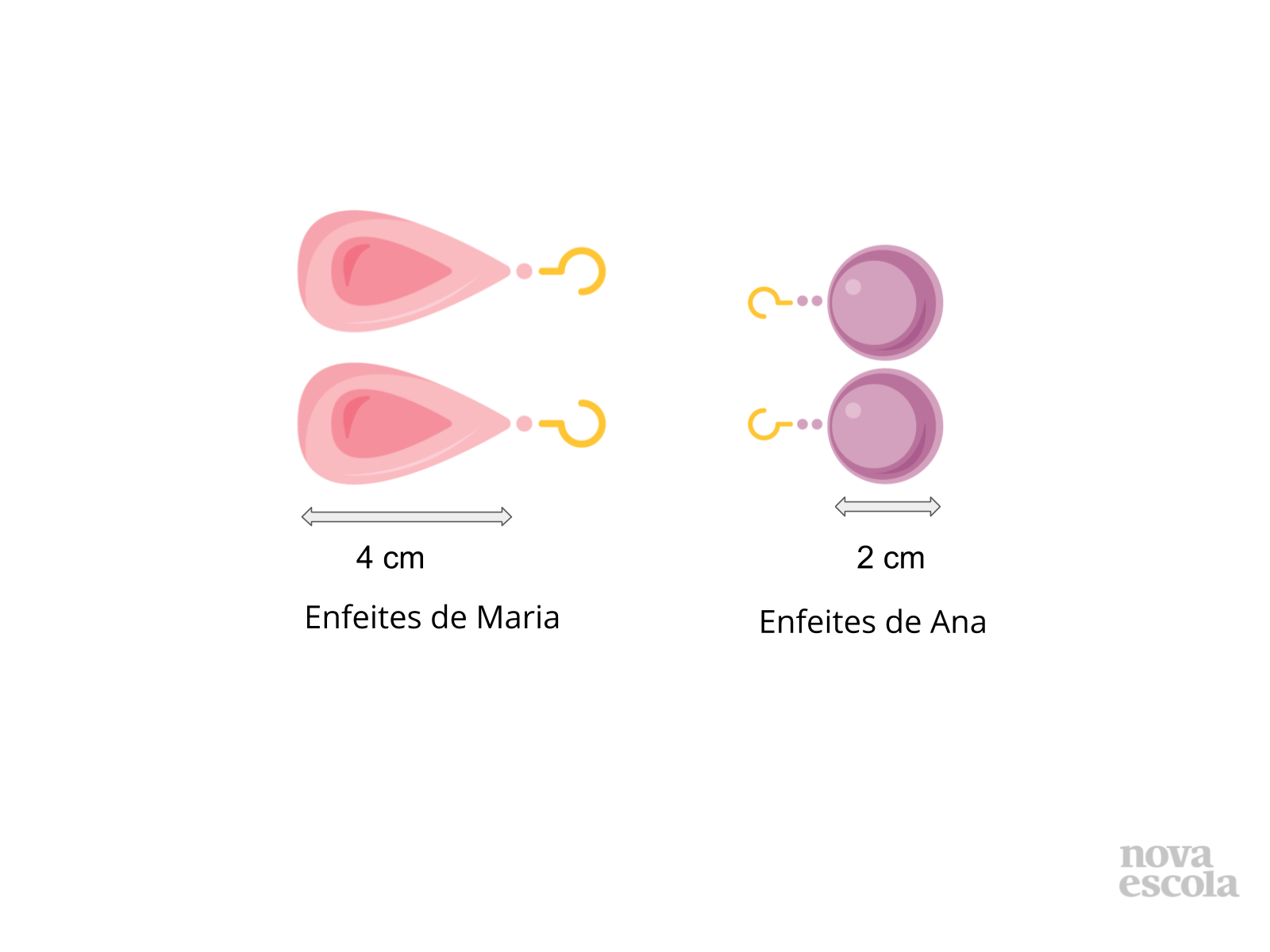
Tempo sugerido: 10 minutos. (Slide 8 e 9).
Orientações: Caso os alunos tenham dificuldade de compreender o enunciado, apresente as imagens, isto poderá auxiliar a resolver este problema.
Propósito: Procurar diferentes estratégias para responder ao problema proposto.
Atividade Principal
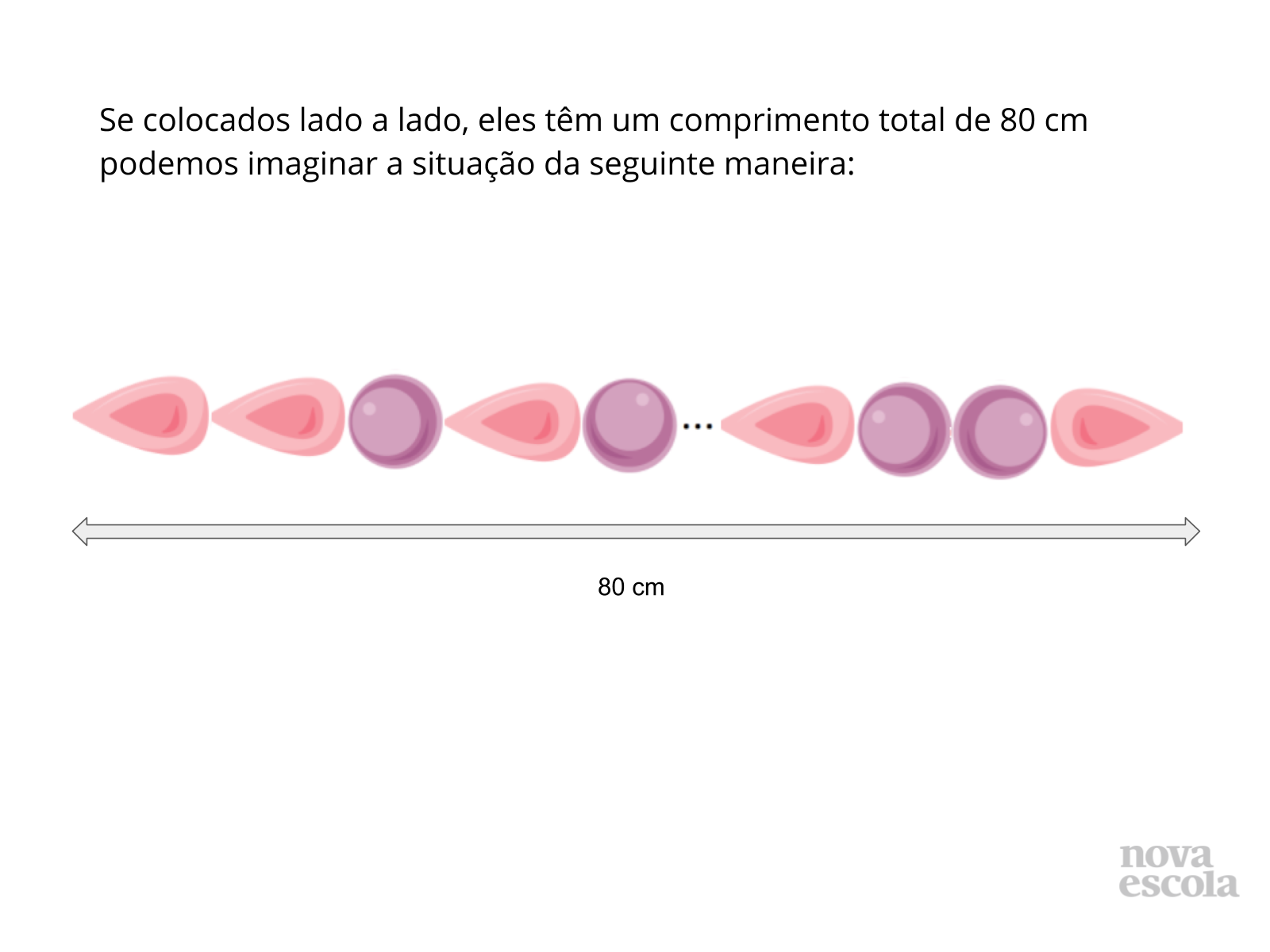
Tempo sugerido: 10 minutos. (Slides 8 e 9).
Orientações: Caso os alunos tenham dificuldade de compreender o enunciado, apresente as imagens, isto poderá auxiliar a resolver este problema.
Propósito: Procurar diferentes estratégias para responder ao problema proposto.
Atividade Principal
Tempo sugerido: 10 minutos.
Orientações: Estimule-os a utilizar uma representação algébrica para poder iniciar a discussão sobre a resolução algébrica do sistema.
Propósito: Procurar diferentes estratégias para responder ao problema proposto.
Discussão das Soluções
Tempo sugerido: 20 minutos.
Orientações: Existe a possibilidade de algum aluno apresentar esta maneira de solucionar o problema proposto. Valorize esta metodologia e mostre que, apesar de eficiente, não é tão prática, uma vez que pode levar muito tempo para encontrar a solução.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Discussão das Soluções
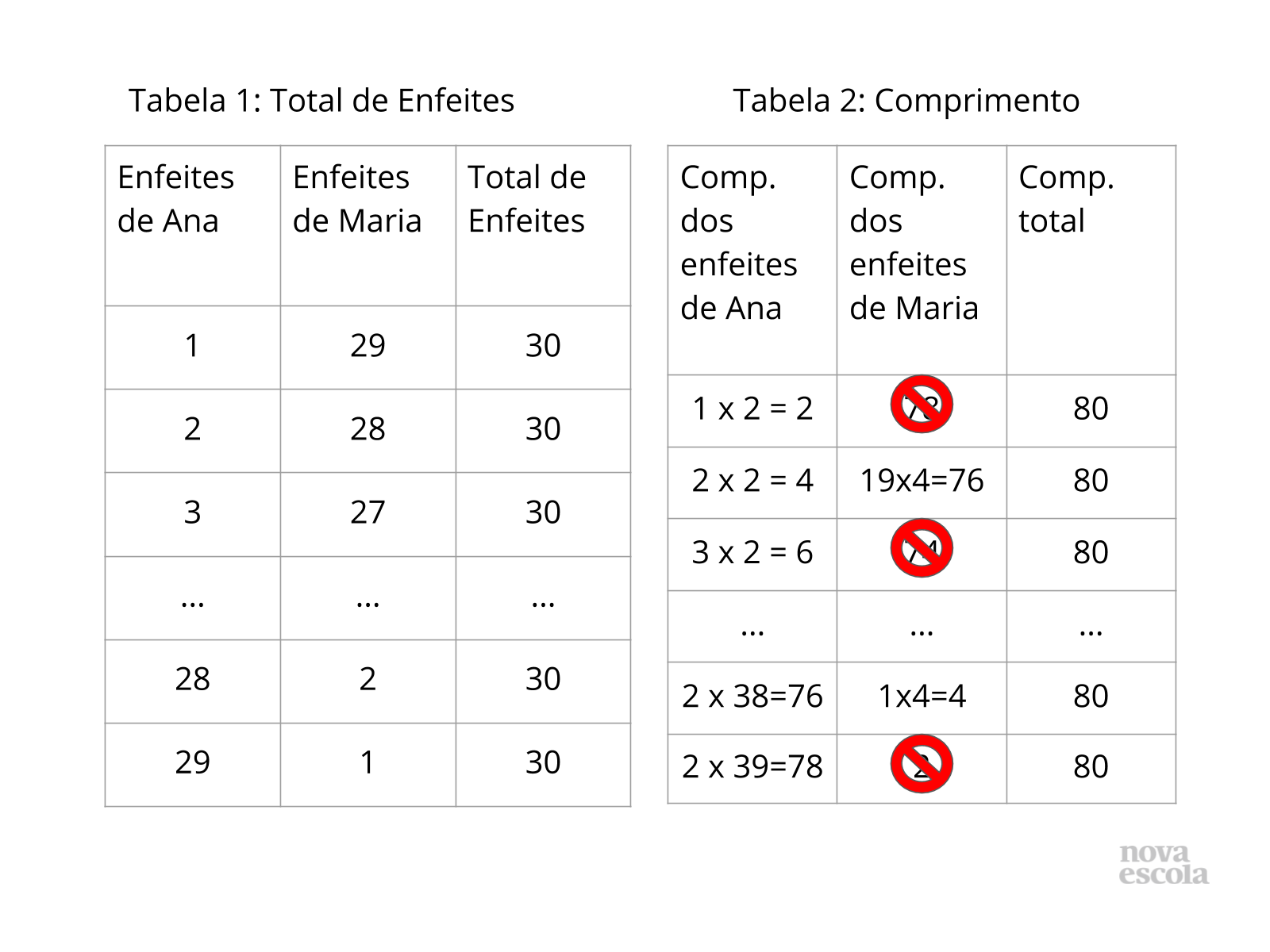
Tempo sugerido: 20 minutos.
Orientações: Existe a possibilidade de algum aluno apresentar esta maneira de solucionar o problema proposto. Valorize esta metodologia e mostre que, apesar de eficiente, não é tão prática, uma vez que pode levar muito tempo para encontrar a solução. Repare que não há um número que multiplicado por 4 resulte em 78 e, por isso, precisamos eliminar esta possibilidade.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Discussão das Soluções
Tempo sugerido: 20 minutos.
Orientações: Existe a possibilidade de algum aluno apresentar esta maneira de solucionar o problema proposto. Valorize esta metodologia e mostre que, apesar de eficiente, não é tão prática, uma vez que pode levar muito tempo para encontrar a solução.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Discussão das Soluções
Tempo sugerido: 20 minutos.
Orientações: Lembre aos alunos que podemos representar valores desconhecidos com letras. Escrever uma situação-problema utilizando uma representação algébrica é uma das questões mais difíceis. Caso os alunos tenham dificuldade de compreender utilizando letras, tente fazer uma tradução lado a lado da língua materna para a linguagem algébrica, ou seja, escreva, de um lado, em português e de outro, em linguagem algébrica. Vá fazendo passo a passo.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Discussão das Soluções
Orientações: Este slide é o momento que antecede a tradução para a linguagem algébrica da segunda restrição ao problema apresentado.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Discussão das Soluções
Orientações: Este slide é o momento que antecede a tradução para a linguagem algébrica da segunda restrição ao problema apresentado.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Discussão das Soluções
Orientações: Este slide é o momento que antecede a tradução para a linguagem algébrica da segunda restrição ao problema apresentado.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
.
Discussão das Soluções
Tempo sugerido: 20 minutos.
Orientações: Caso o aluno encontre uma outra maneira de representar a situação, observe qual é a dificuldade apresentada e oriente-o da melhor maneira possível.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Discussão das Soluções
Tempo sugerido: 20 minutos.
Orientações: Este é um momento importante, apresente aos alunos como se representa um sistema de equações lineares e que esta simbologia representa que o resultado precisa satisfazer todos os casos compreendidos na chave.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Discussão das Soluções
Tempo sugerido: 20 minutos.
Orientações: Lembre os alunos que, se conhecêssemos o número de enfeites produzidos por Maria, não seria difícil determinar o valor de A. Sendo assim, utilizamos a mesma estratégia de uma equação com apenas uma incógnita normalmente. A diferença é que neste caso, ao invés de apresentar uma resposta numérica, o número de enfeites de Ana está representado pela diferença entre o total de enfeites e o número de enfeites de Maria.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Discussão das Soluções
Tempo sugerido: 20 minutos.
Orientações: É possível que os alunos não compreendam o motivo de realizar a substituição. Mostre que, com isso, a nova equação possui apenas uma incógnita a ser determinada. Outra situação possível é que os alunos não vejam a razão de ser possível substituir o valor de A pela expressão 30-M. Neste caso, mostre que são valores equivalentes.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Discussão das Soluções
Tempo sugerido: 20 minutos.
Orientações: Relembre com os alunos a propriedade distributiva da multiplicação.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Discussão das Soluções
Tempo sugerido: 20 minutos.
Orientações: Mostre que, sabendo o valor de M, a expressão algébrica que representa o valor de A passa a ser uma expressão numérica, onde podemos determinar seu valor, uma vez que basta substituir na expressão, o valor de M.
Propósito: Comentar resoluções alternativas e mostrar as vantagens e desvantagens.
Sistematização do Conceito
Tempo sugerido: 5 minutos.
Orientações: Antes de comentar o que está sendo dito no slide, pergunte o que aconteceu com a equação após a substituição ser realizada. Depois que os alunos perceberem que agora temos uma equação com apenas um valor desconhecido, pergunte para eles se isso acontecerá sempre, ou se isso foi por acaso. Isso proporciona um sentido de generalização onde os alunos vão reconhecer que isso não acontece apenas nesse caso específico, mas também em todas as situações em que podemos resolver o problema a partir de um sistema de equações.
Propósito: Revisitar e generalizar o conceito abordado nesta aula.
Encerramento
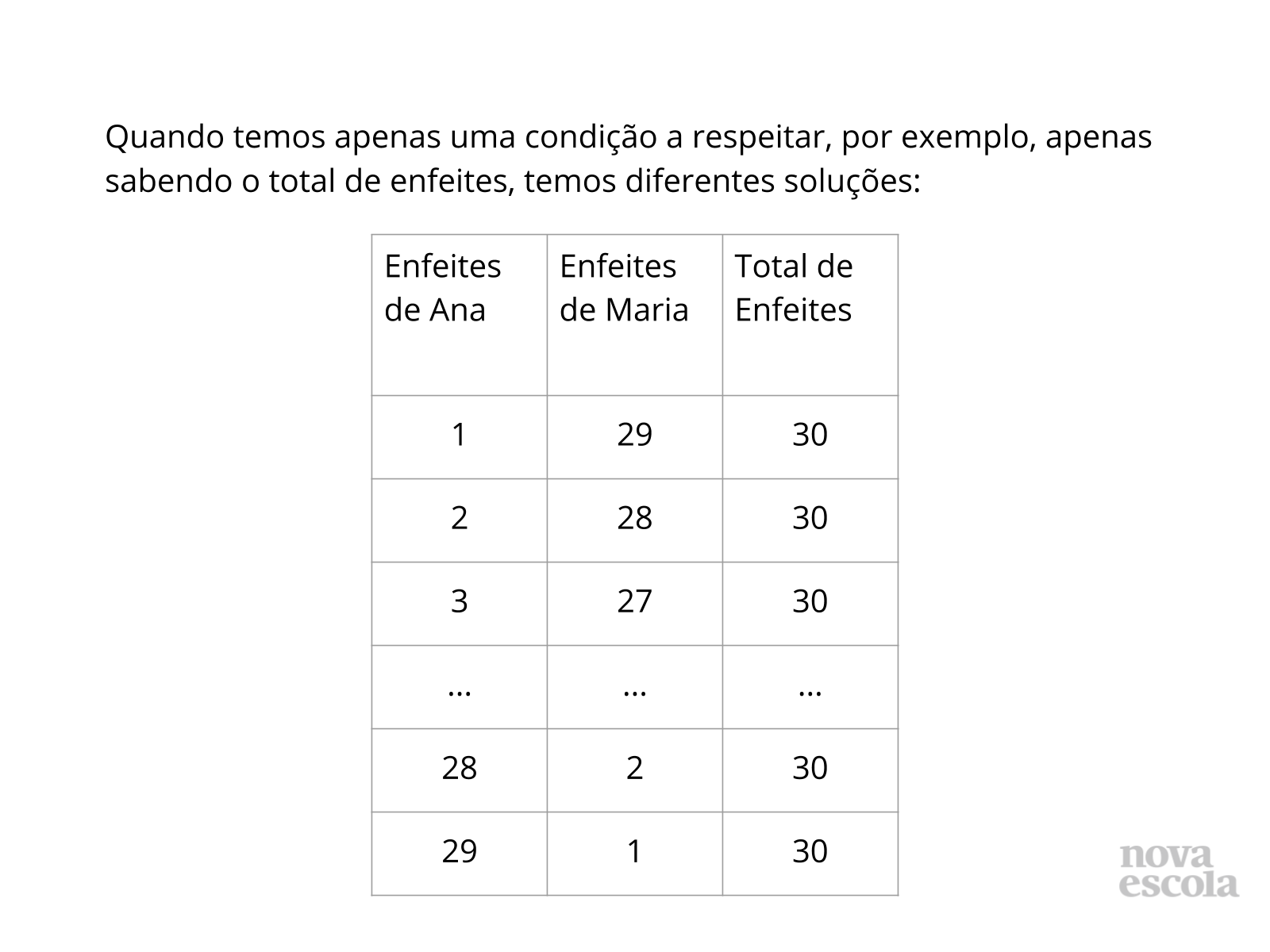
Tempo sugerido: 5 minutos. (Slides 24 e 25).
Orientações: Os alunos estão acostumados a encontrar um conjunto de soluções para cada um dos problemas apresentados desde a aula anterior. Neste caso, determine, juntando as duas condições, um único número de enfeites feitos por Maria e outro que responda a pergunta feita. A resposta, neste caso, seria um único par de números. Caso não seja possível projetar essa situação, coloque as tabelas em um papel pardo para que todos possam ver o que acontece. Não precisa ter a tabela completa, pois o objetivo não é resolver utilizando a tabela, mas é interessante que os alunos percebam que as duas condições sozinhas nos oferecem várias soluções.
Propósito: Mostrar a diferença entre variável e incógnita.
Encerramento
Tempo sugerido: 5 minutos. (Slides 24 e 25).
Orientações: Os alunos estão acostumados a encontrar um conjunto de soluções para cada um dos problemas apresentados desde a aula anterior. Neste caso, determine, juntando as duas condições, um único número de enfeites feitos por Maria e outro que responda a pergunta feita. A resposta, neste caso, seria um único par de números. Caso não seja possível projetar essa situação, coloque as tabelas em um papel pardo para que todos possam ver o que acontece. Não precisa ter a tabela completa, pois o objetivo não é resolver utilizando a tabela, mas é interessante que os alunos percebam que as duas condições sozinhas nos oferecem várias soluções.
Propósito: Mostrar a diferença entre variável e incógnita.
Encerramento
Tempo sugerido: 5 minutos.
Orientações: Os alunos estão acostumados a encontrar um conjunto de soluções para cada um dos problemas apresentados desde a aula anterior. Neste caso, juntando as duas condições, determine um único número de enfeites feitos por Maria e outro que responda a pergunta feita. A resposta, neste caso, seria um único par de números.
Propósito: Mostrar a diferença entre variável e incógnita.
Raio X
Tempo sugerido: 8 minutos.
Orientações: Apresente o novo problema e pergunte aos alunos quais as estratégias que podem ser traçadas para resolver o problema. Pergunte, também, se é possível determinar a resposta em uma primeira tentativa estimada, ou seja, se eles têm uma estimativa para o resultado.
Propósito: Auxiliar os alunos a perceber que existe uma única solução para o problema proposto.
Discuta com a turma:
- Quais as diferentes maneiras para que o problema possa ser resolvido?
- Quais as relações lineares estabelecidas?
- Quais as restrições impostas?
- Por que não pode ser outra resposta?
Materiais Complementares:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
