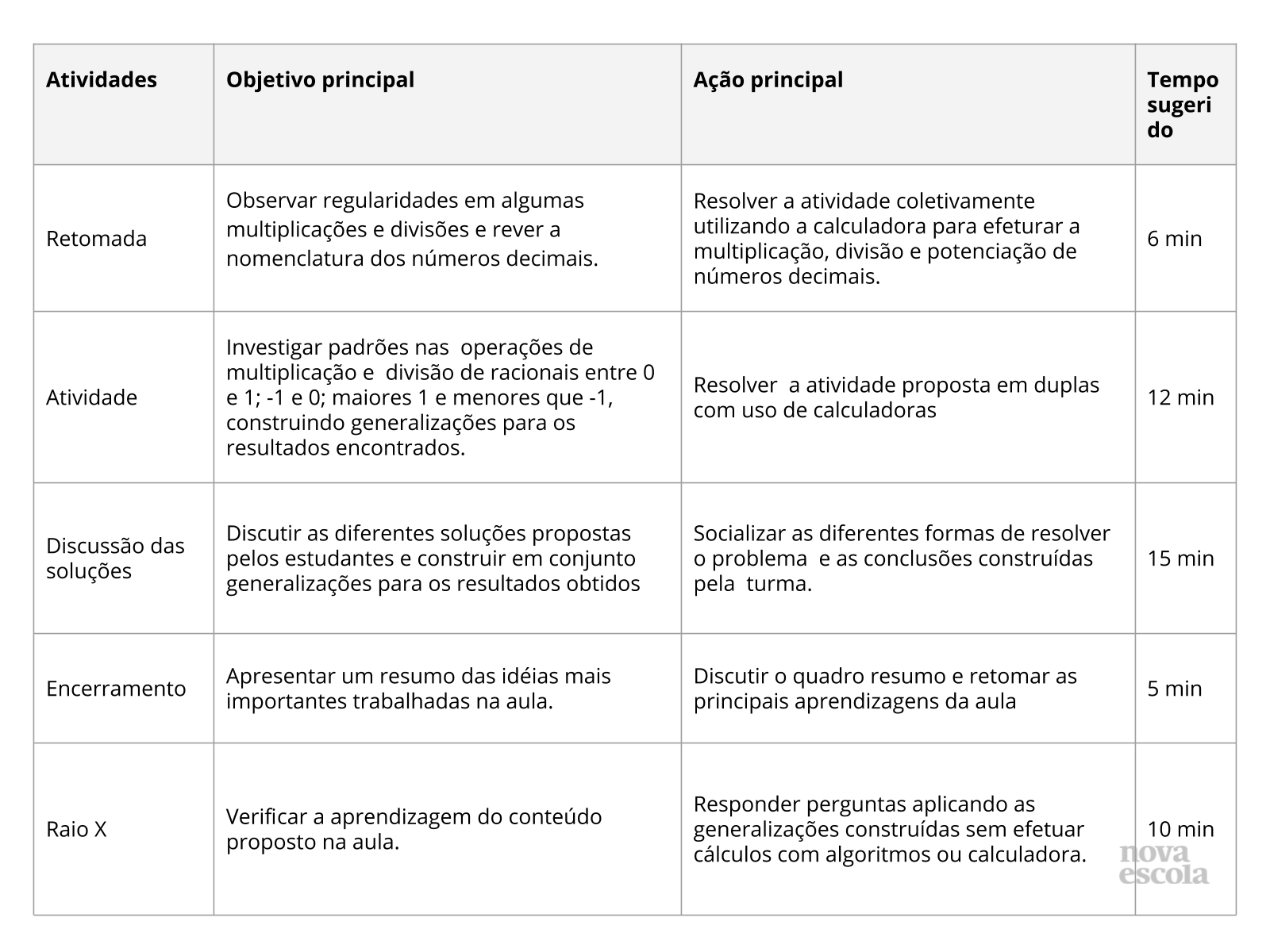
Retomada
Plano de Aula
Plano de aula: O QUE EXISTE ENTRE ZERO E UM?
Plano 3 de uma sequência de 5 planos. Veja todos os planos sobre Operações aritméticas com números inteiros e racionais
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
Cálculo das quatro operações e potenciação com números inteiros e racionais ( fluência em cálculo mental; escrito e aproximado ou calculadora)
Objetivos específicos
Estabelecer generalizações para a multiplicação e a divisão de racionais na forma decimal entre zero e um, maiores que um e menores que -1 usando estimativas mentais e calculadora.
Conceito-chave
Multiplicação, divisão, intervalo [0,1], falsas generalizações.
Recursos necessários
- Projetor (caso haja)
- Calculadoras;
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
Estabelecer generalizações para a multiplicação e a divisão de racionais na forma decimal entre zero e um, maiores que um e menores que -1 usando estimativas mentais e calculadora.
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 6 minutos. (slides 3 a 5)
Orientações: Antes de iniciar, organize a sala em forma de meia lua em torno do quadro. Inicie então este momento da aula fazendo aos alunos o questionamento do slide 3. Deixe que pensem por um tempo e anote algumas considerações deles no quadro, para validá-las ou refutá-las ao fim da aula.
Em seguida, entregue uma cópia impressa da atividade e/ou projete o slide 4. Peça então para que os alunos peguem suas calculadoras (que deverá ser solicitada em aulas anteriores) e efetuem os cálculos, anotando os resultados na tabela da atividade que receberam. Em seguida, peça para que respondam nos espaços da folha que foi entregue o item B.
Pergunte então o que eles reponderam nos dois tópicos do item B. Deixe os alunos à vontade, por mais que tenham respondido errado, pois assim, poderão logo depois corrigir seus erros e aprender como evitá-los.
Passe então para o slide 5 e leia junto dos alunos as informações sobre os tópicos do item B, apresentadas no balão da fala da personagem.
Propósito: Retomar os conhecimentos e habilidades necessários para uma boa compreensão da aula.
Discuta com a turma:
- Qual o menor número que você obteve? E o maior?
- No objetivo da aula apresentado pela classe fala apenas de multiplicação e divisão. Que justificativa podemos dar para que a potenciação esteja contemplada na atividade?
Possível resposta: Por definição, a potenciação é uma multiplicação de fatores iguais. E a multiplicação está contemplada em nosso objetivo para esta aula.
- Uma das funções da calculadora é agilizar alguns processos mecânicos de cálculos que demoraram muito para fazer manualmente, ela dá resultados precisos com bastante rapidez. Nessa aula qual será a função da calculadora?
Possível Resposta: A calculadora irá nos auxiliar na investigação de alguns padrões que vamos encontrar em nossa atividade, também vai dar agilidade para os cálculos a serem feitos, se tivéssemos que efetuar os cálculos manualmente demandaria uma quantidade excessiva de tempo.
Materiais complementares:
Retomada
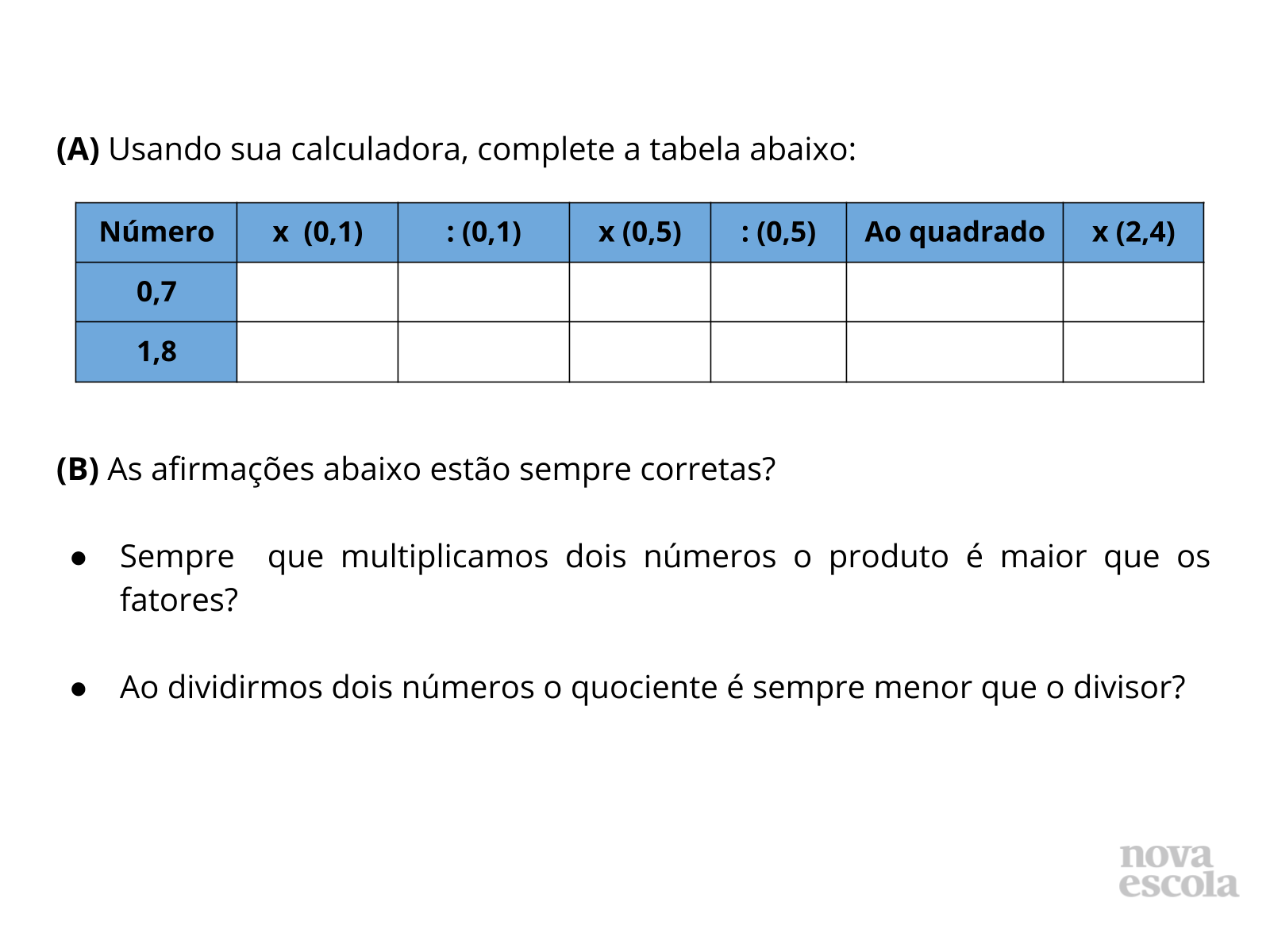
Tempo sugerido: 6 minutos. (slides 3 a 5)
Orientações: Antes de iniciar, organize a sala em forma de meia lua em torno do quadro. Inicie então este momento da aula fazendo aos alunos o questionamento do slide 3. Deixe que pensem por um tempo e anote algumas considerações deles no quadro, para validá-las ou refutá-las ao fim da aula.
Em seguida, entregue uma cópia impressa da atividade e/ou projete o slide 4. Peça então para que os alunos peguem suas calculadoras (que deverá ser solicitada em aulas anteriores) e efetuem os cálculos, anotando os resultados na tabela da atividade que receberam. Em seguida, peça para que respondam nos espaços da folha que foi entregue o item B.
Pergunte então o que eles reponderam nos dois tópicos do item B. Deixe os alunos à vontade, por mais que tenham respondido errado, pois assim, poderão logo depois corrigir seus erros e aprender como evitá-los.
Passe então para o slide 5 e leia junto dos alunos as informações sobre os tópicos do item B, apresentadas no balão da fala da personagem.
Propósito: Retomar os conhecimentos e habilidades necessários para uma boa compreensão da aula.
Discuta com a turma:
- Qual o menor número que você obteve? E o maior?
- No objetivo da aula apresentado pela classe fala apenas de multiplicação e divisão. Que justificativa podemos dar para que a potenciação esteja contemplada na atividade?
Possível resposta: Por definição, a potenciação é uma multiplicação de fatores iguais. E a multiplicação está contemplada em nosso objetivo para esta aula.
- Uma das funções da calculadora é agilizar alguns processos mecânicos de cálculos que demoraram muito para fazer manualmente, ela dá resultados precisos com bastante rapidez. Nessa aula qual será a função da calculadora?
Possível Resposta: A calculadora irá nos auxiliar na investigação de alguns padrões que vamos encontrar em nossa atividade, também vai dar agilidade para os cálculos a serem feitos, se tivéssemos que efetuar os cálculos manualmente demandaria uma quantidade excessiva de tempo.
Retomada
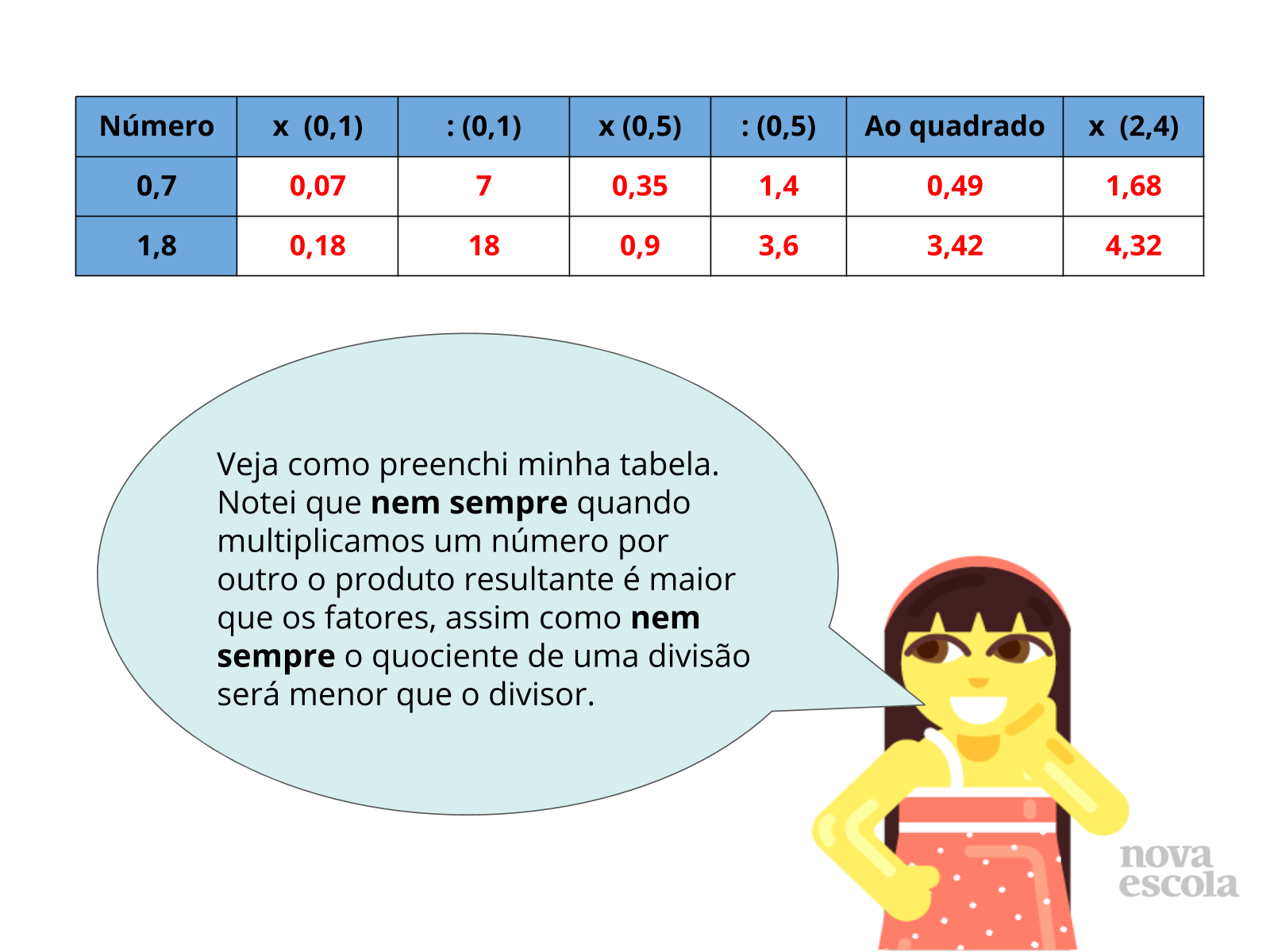
Tempo sugerido: 6 minutos. (slides 3 a 5)
Orientações: Antes de iniciar, organize a sala em forma de meia lua em torno do quadro. Inicie então este momento da aula fazendo aos alunos o questionamento do slide 3. Deixe que pensem por um tempo e anote algumas considerações deles no quadro, para validá-las ou refutá-las ao fim da aula.
Em seguida, entregue uma cópia impressa da atividade e/ou projete o slide 4. Peça então para que os alunos peguem suas calculadoras (que deverá ser solicitada em aulas anteriores) e efetuem os cálculos, anotando os resultados na tabela da atividade que receberam. Em seguida, peça para que respondam nos espaços da folha que foi entregue o item B.
Pergunte então o que eles reponderam nos dois tópicos do item B. Deixe os alunos à vontade, por mais que tenham respondido errado, pois assim, poderão logo depois corrigir seus erros e aprender como evitá-los.
Passe então para o slide 5 e leia junto dos alunos as informações sobre os tópicos do item B, apresentadas no balão da fala da personagem.
Propósito: Retomar os conhecimentos e habilidades necessários para uma boa compreensão da aula.
Discuta com a turma:
- Qual o menor número que você obteve? E o maior?
- No objetivo da aula apresentado pela classe fala apenas de multiplicação e divisão. Que justificativa podemos dar para que a potenciação esteja contemplada na atividade?
Possível resposta: Por definição, a potenciação é uma multiplicação de fatores iguais. E a multiplicação está contemplada em nosso objetivo para esta aula.
- Uma das funções da calculadora é agilizar alguns processos mecânicos de cálculos que demoraram muito para fazer manualmente, ela dá resultados precisos com bastante rapidez. Nessa aula qual será a função da calculadora?
Possível Resposta: A calculadora irá nos auxiliar na investigação de alguns padrões que vamos encontrar em nossa atividade, também vai dar agilidade para os cálculos a serem feitos, se tivéssemos que efetuar os cálculos manualmente demandaria uma quantidade excessiva de tempo.
Atividade principal

Tempo sugerido: 15 minutos (slides 6 e 7)
Orientações: Projete e/ou entregue uma cópia impressa da atividade, aos alunos e faça uma leitura conjunta. Peça então para que iniciem a resolução da atividade individualmente. Solicite também para que utilizem a calculadora para encontrar o resultado do item “Leitura no display” da atividade.
Após responderem, passados cerca de 10 minutos de atividade, solicite que os alunos respondam o item B e compartilhem suas respostas com colegas próximos.
Enquanto os alunos respondem toda a atividade, circule pela sala para tirar suas eventuais dúvidas e ajudar aqueles que estão com dificuldades. Consulte o guia de intervenções para verificar sugestões de como mediar a resolução da atividade sem dar a resposta certa ao aluno, mas estimulando-o a pensar matematicamente.
Propósito: Fazer com que os alunos trabalhem individualmente e em grupo em busca da resolução da atividade e da ampliação de conhecimentos.
Discuta com a truma:
- Esta atividade foi criada para ser desenvolvida em um ambiente colaborativo onde todos aprendem com todos, então todos devem contribuir tentando resolver a atividade solicitando ajuda do professor ou dos colegas sempre que precisar.
Materiais complementares:
Atividade principal
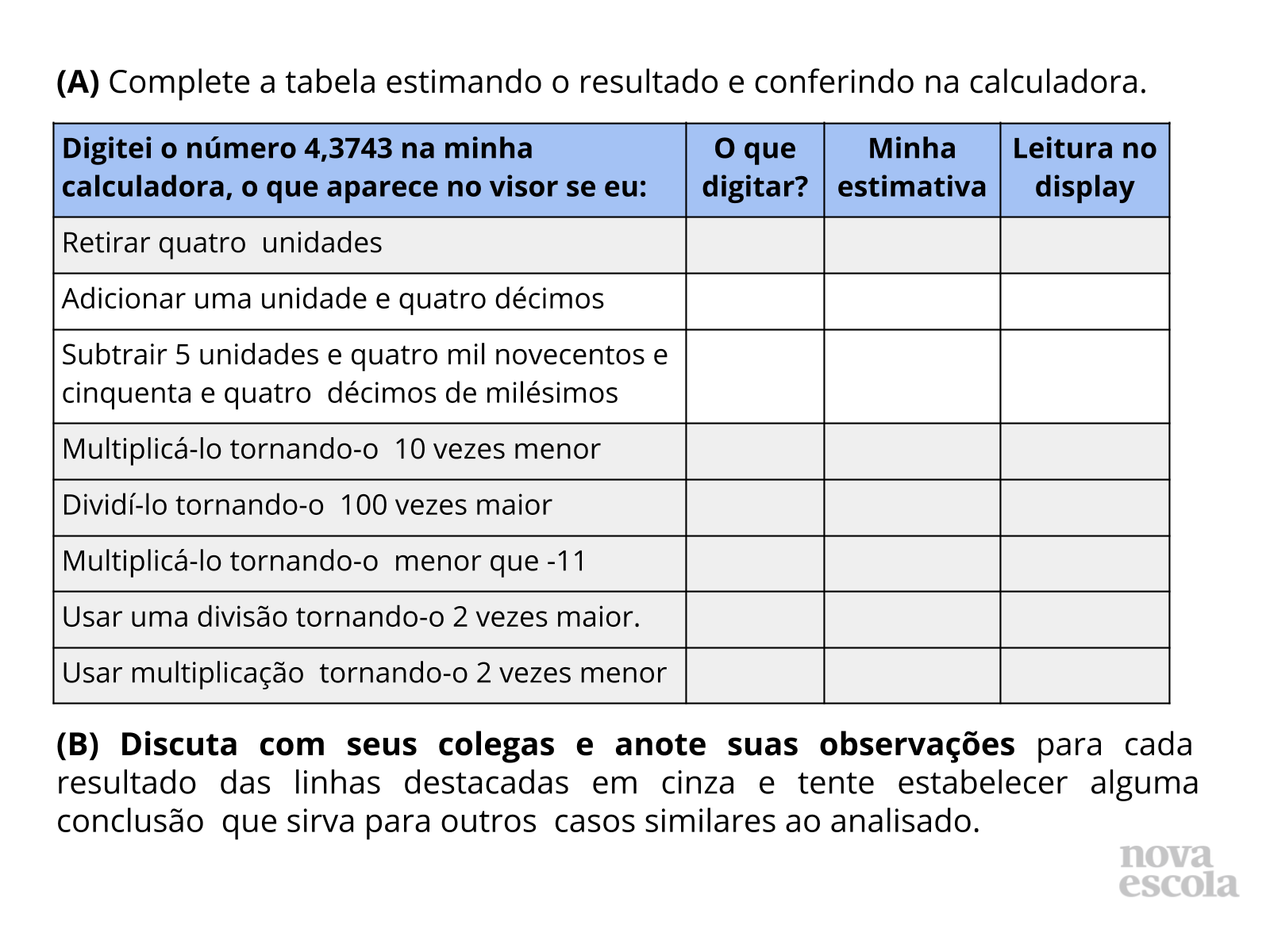
Tempo sugerido: 15 minutos (slides 6 e 7)
Orientações: Projete e/ou entregue uma cópia impressa da atividade, aos alunos e faça uma leitura conjunta. Peça então para que iniciem a resolução da atividade individualmente. Solicite também para que utilizem a calculadora para encontrar o resultado do item “Leitura no display” da atividade.
Após responderem, passados cerca de 10 minutos de atividade, solicite que os alunos respondam o item B e compartilhem suas respostas com colegas próximos.
Enquanto os alunos respondem toda a atividade, circule pela sala para tirar suas eventuais dúvidas e ajudar aqueles que estão com dificuldades. Consulte o guia de intervenções para verificar sugestões de como mediar a resolução da atividade sem dar a resposta certa ao aluno, mas estimulando-o a pensar matematicamente.
Propósito: Fazer com que os alunos trabalhem individualmente e em grupo em busca da resolução da atividade e da ampliação de conhecimentos.
Discuta com a truma:
- A responsabilidade pelo aprendizado é individual, portanto, os estudantes devem ter consciência de que o esforço na resolução tem que ser seu e não esperar um colega próximo fazer e copiar o resultado. A atividade é desenvolvida em um ambiente colaborativo onde todos aprendem com todos, então todos devem contribuir tentando resolver a atividade solicitando ajuda do professor ou dos colegas sempre que precisar.
Discussão da solução
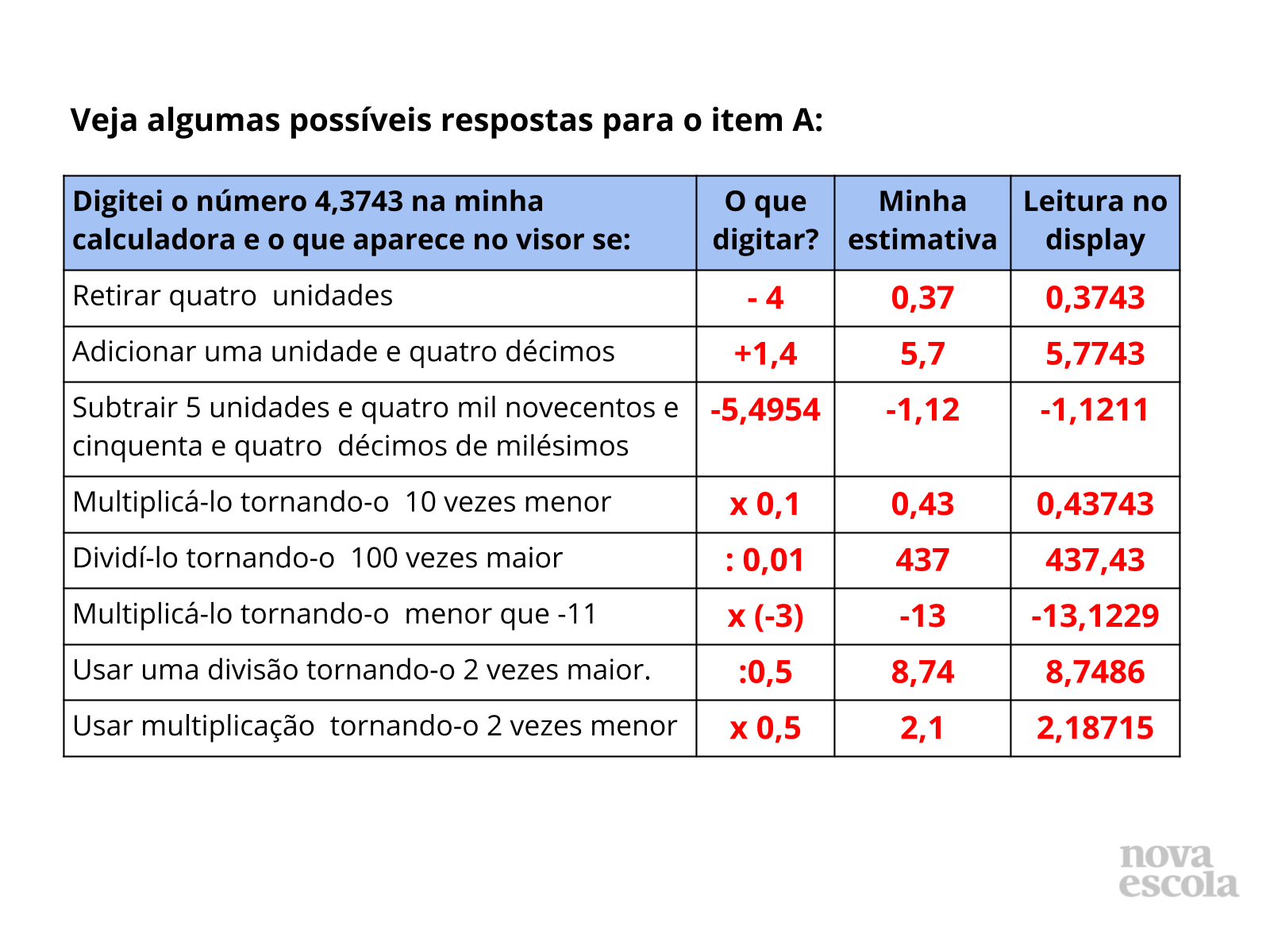
Tempo sugerido: 12 minutos (slides 8 a 12)
Orientações: Convide os alunos para apresentar suas tabelas, especialmente suas estimativas, se acertaram muitas, poucas ou quais foram. Em seguida, peça que compartilhem suas conclusões no item B e também que justifiquem o motivo de cada uma delas, ainda que tenham feito errado ou apresentem dúvidas, pois esse será o momento mais adequado para verificar como e porque os erros ocorreram. Valorize a participação dos alunos, provoque um debate matemático, sempre que alguém apresentar uma solução, pergunte se outros fizeram do mesmo jeito ou diferente. Caso os alunos não consigam alcançar argumentos satisfatórios sozinhos faça as devidas intervenções até que consigam atingir os objetivos propostos para a aula.
Nos slides 9 a 12, você encontra sugestões de respostas para todos os casos estudados na atividade, se necessário, aborde os tópicos disponíveis nesses slides a fim de justificar e apresentar possibilidades para determinadas respostas da atividade.
Propósito: Apresentar e discutir diferentes soluções para a atividade principal.
Discuta com a turma:
- É importante buscar sempre fazer uma estimativa mental do resultado antes de realizarmos um cálculo?
Possível resposta: É importante, afinal, teremos um valor próximo do correto, assim, se cometermos um erro ao fazer a conta, saberemos vendo que o resultado está muito distante daquele que foi estimado.
- Por que o zero é uma exceção nas linhas 7 e 8?
Possível resposta: Zero multiplicado por qualquer número, é sempre zero, e se dividido por qualquer número diferente de zero também é zero. Mas se qualquer número, for dividido por zero, teremos uma indeterminação.
Discussão da solução

Tempo sugerido: 12 minutos (slides 8 a 12)
Orientações: Convide os alunos para apresentar suas tabelas, especialmente suas estimativas, se acertaram muitas, poucas ou quais foram. Em seguida, peça que compartilhem suas conclusões no item B e também que justifiquem o motivo de cada uma delas, ainda que tenham feito errado ou apresentem dúvidas, pois esse será o momento mais adequado para verificar como e porque os erros ocorreram. Valorize a participação dos alunos, provoque um debate matemático, sempre que alguém apresentar uma solução, pergunte se outros fizeram do mesmo jeito ou diferente. Caso os alunos não consigam alcançar argumentos satisfatórios sozinhos faça as devidas intervenções até que consigam atingir os objetivos propostos para a aula.
Nos slides 9 a 12, você encontra sugestões de respostas para todos os casos estudados na atividade, se necessário, aborde os tópicos disponíveis nesses slides a fim de justificar e apresentar possibilidades para determinadas respostas da atividade.
Propósito: Apresentar e discutir diferentes soluções para a atividade principal.
Discuta com a turma:
- É importante buscar sempre fazer uma estimativa mental do resultado antes de realizarmos um cálculo?
Possível resposta: É importante, afinal, teremos um valor próximo do correto, assim, se cometermos um erro ao fazer a conta, saberemos vendo que o resultado está muito distante daquele que foi estimado.
- Por que o zero é uma exceção nas linhas 7 e 8?
Possível resposta: Zero multiplicado por qualquer número, é sempre zero, e se dividido por qualquer número diferente de zero também é zero. Mas se qualquer número, for dividido por zero, teremos uma indeterminação.
Discussão da solução

Tempo sugerido: 12 minutos (slides 8 a 12)
Orientações: Convide os alunos para apresentar suas tabelas, especialmente suas estimativas, se acertaram muitas, poucas ou quais foram. Em seguida, peça que compartilhem suas conclusões no item B e também que justifiquem o motivo de cada uma delas, ainda que tenham feito errado ou apresentem dúvidas, pois esse será o momento mais adequado para verificar como e porque os erros ocorreram. Valorize a participação dos alunos, provoque um debate matemático, sempre que alguém apresentar uma solução, pergunte se outros fizeram do mesmo jeito ou diferente. Caso os alunos não consigam alcançar argumentos satisfatórios sozinhos faça as devidas intervenções até que consigam atingir os objetivos propostos para a aula.
Nos slides 9 a 12, você encontra sugestões de respostas para todos os casos estudados na atividade, se necessário, aborde os tópicos disponíveis nesses slides a fim de justificar e apresentar possibilidades para determinadas respostas da atividade.
Propósito: Apresentar e discutir diferentes soluções para a atividade principal.
Discuta com a turma:
- É importante buscar sempre fazer uma estimativa mental do resultado antes de realizarmos um cálculo?
Possível resposta: É importante, afinal, teremos um valor próximo do correto, assim, se cometermos um erro ao fazer a conta, saberemos vendo que o resultado está muito distante daquele que foi estimado.
- Por que o zero é uma exceção nas linhas 7 e 8?
Possível resposta: Zero multiplicado por qualquer número, é sempre zero, e se dividido por qualquer número diferente de zero também é zero. Mas se qualquer número, for dividido por zero, teremos uma indeterminação.
Discussão da solução

Tempo sugerido: 12 minutos (slides 8 a 12)
Orientações: Convide os alunos para apresentar suas tabelas, especialmente suas estimativas, se acertaram muitas, poucas ou quais foram. Em seguida, peça que compartilhem suas conclusões no item B e também que justifiquem o motivo de cada uma delas, ainda que tenham feito errado ou apresentem dúvidas, pois esse será o momento mais adequado para verificar como e porque os erros ocorreram. Valorize a participação dos alunos, provoque um debate matemático, sempre que alguém apresentar uma solução, pergunte se outros fizeram do mesmo jeito ou diferente. Caso os alunos não consigam alcançar argumentos satisfatórios sozinhos faça as devidas intervenções até que consigam atingir os objetivos propostos para a aula.
Nos slides 9 a 12, você encontra sugestões de respostas para todos os casos estudados na atividade, se necessário, aborde os tópicos disponíveis nesses slides a fim de justificar e apresentar possibilidades para determinadas respostas da atividade.
Propósito: Apresentar e discutir diferentes soluções para a atividade principal.
Discuta com a turma:
- É importante buscar sempre fazer uma estimativa mental do resultado antes de realizarmos um cálculo?
Possível resposta: É importante, afinal, teremos um valor próximo do correto, assim, se cometermos um erro ao fazer a conta, saberemos vendo que o resultado está muito distante daquele que foi estimado.
- Por que o zero é uma exceção nas linhas 7 e 8?
Possível resposta: Zero multiplicado por qualquer número, é sempre zero, e se dividido por qualquer número diferente de zero também é zero. Mas se qualquer número, for dividido por zero, teremos uma indeterminação.
Discussão da solução

Tempo sugerido: 12 minutos (slides 8 a 12)
Orientações: Convide os alunos para apresentar suas tabelas, especialmente suas estimativas, se acertaram muitas, poucas ou quais foram. Em seguida, peça que compartilhem suas conclusões no item B e também que justifiquem o motivo de cada uma delas, ainda que tenham feito errado ou apresentem dúvidas, pois esse será o momento mais adequado para verificar como e porque os erros ocorreram. Valorize a participação dos alunos, provoque um debate matemático, sempre que alguém apresentar uma solução, pergunte se outros fizeram do mesmo jeito ou diferente. Caso os alunos não consigam alcançar argumentos satisfatórios sozinhos faça as devidas intervenções até que consigam atingir os objetivos propostos para a aula.
Nos slides 9 a 12, você encontra sugestões de respostas para todos os casos estudados na atividade, se necessário, aborde os tópicos disponíveis nesses slides a fim de justificar e apresentar possibilidades para determinadas respostas da atividade.
Propósito: Apresentar e discutir diferentes soluções para a atividade principal.
Discuta com a turma:
- É importante buscar sempre fazer uma estimativa mental do resultado antes de realizarmos um cálculo?
Possível resposta: É importante, afinal, teremos um valor próximo do correto, assim, se cometermos um erro ao fazer a conta, saberemos vendo que o resultado está muito distante daquele que foi estimado.
- Por que o zero é uma exceção nas linhas 7 e 8?
Possível resposta: Zero multiplicado por qualquer número, é sempre zero, e se dividido por qualquer número diferente de zero também é zero. Mas se qualquer número, for dividido por zero, teremos uma indeterminação.
Encerramento

Tempo sugerido: 5 minutos (slides 13 a 15)
Orientações: O conteúdo dos slides 13 a 15 concentram os principais conceitos contemplados nesta aula. Explique o texto dos slides, verifique se ainda há dúvidas, e esclareça-as, pois o próximo momento da aula é a verificação da aprendizagem por meio do raio x.
Propósito: Fazer o fechamento da ideias desenvolvidas durante a resolução das atividades da aula.
Discuta com a turma:
- Questione ainda há alguma dúvida.
- Enfatize e discuta junto com a turma as conclusões para racionais negativos.
- O que foi alterado em sua compreensão após a atividade principal?
Encerramento

Tempo sugerido: 5 minutos (slides 13 a 15)
Orientações: O conteúdo dos slides 13 a 15 concentram os principais conceitos contemplados nesta aula. Explique o texto dos slides, verifique se ainda há dúvidas, e esclareça-as, pois o próximo momento da aula é a verificação da aprendizagem por meio do raio x.
Propósito: Fazer o fechamento da ideias desenvolvidas durante a resolução das atividades da aula.
Discuta com a turma:
- Questione ainda há alguma dúvida.
- Enfatize e discuta junto com a turma as conclusões para racionais negativos.
- O que foi alterado em sua compreensão após a atividade principal?
Encerramento

Tempo sugerido: 5 minutos (slides 13 a 15)
Orientações: O conteúdo dos slides 13 a 15 concentram os principais conceitos contemplados nesta aula. Explique o texto dos slides, verifique se ainda há dúvidas, e esclareça-as, pois o próximo momento da aula é a verificação da aprendizagem por meio do raio x.
Propósito: Fazer o fechamento da ideias desenvolvidas durante a resolução das atividades da aula.
Discuta com a turma:
- Questione ainda há alguma dúvida.
- Enfatize e discuta junto com a turma as conclusões para racionais negativos.
- O que foi alterado em sua compreensão após a atividade principal?
Atividade de Raio X

Tempo sugerido: 10 minutos.
Orientação: Leia junto dos alunos o enunciado da atividade e verifiquem se todos compreenderam o problema e sabem o que devem fazer, e pedir para que resolvam. Circule pela sala para verificar as resoluções. Lembre-se que neste momento você está avaliando os avanços dos estudantes em relação ao conteúdo da aula. Procure identificar as dúvidas que ainda ficaram e reserve os 3 minutos finais da aula para uma breve correção desta atividade.
Propósito: Verificar a assimilação dos conteúdos desenvolvidos durante a aula.
Materiais complementares:
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
Cálculo das quatro operações e potenciação com números inteiros e racionais ( fluência em cálculo mental; escrito e aproximado ou calculadora)
Objetivos específicos
Estabelecer generalizações para a multiplicação e a divisão de racionais na forma decimal entre zero e um, maiores que um e menores que -1 usando estimativas mentais e calculadora.
Conceito-chave
Multiplicação, divisão, intervalo [0,1], falsas generalizações.
Recursos necessários
- Projetor (caso haja)
- Calculadoras;
- Atividades impressas em folhas, coladas no caderno ou não.










