Retomada
Plano de Aula
Plano de aula: Interpretando Visualmente Operações Racionais.
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Operações aritméticas com números inteiros e racionais
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
( a definir) .Cálculo das quatro operações e potenciação com números inteiros e racionais (fluência em cálculo mental; escrito e aproximado ou calculadora)
Objetivos Específicos
Resolver e interpretar problemas aplicando as operações de adição, subtração, multiplicação e divisão de racionais nas formas fracionária e decimal.
Conceito-chave
Fração, número decimal, multiplicação, divisão.
Recursos Necessários
- Projetor (caso haja)
- Calculadoras;
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
( a definir) .Cálculo das quatro operações e potenciação com números inteiros e racionais (fluência em cálculo mental; escrito e aproximado ou calculadora)
Objetivos Específicos
Resolver e interpretar problemas aplicando as operações de adição, subtração, multiplicação e divisão de racionais nas formas fracionária e decimal.
Conceito-chave
Fração, número decimal, multiplicação, divisão.
Recursos Necessários
- Projetor (caso haja)
- Calculadoras;
- Atividades impressas em folhas, coladas no caderno ou não.
Resumo da aula
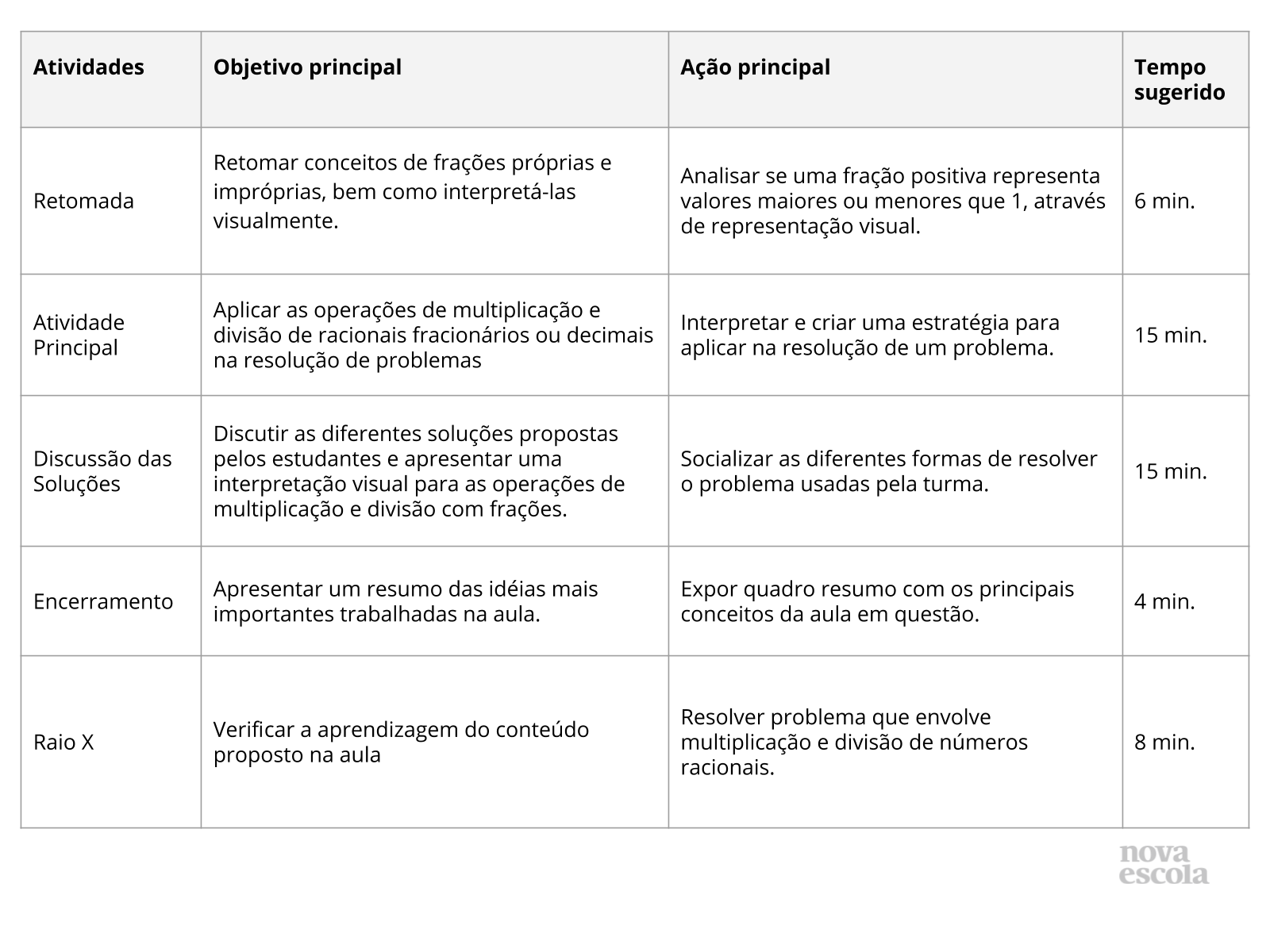
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
Tempo sugerido: 6 minutos (slides 3, 4 e 5)
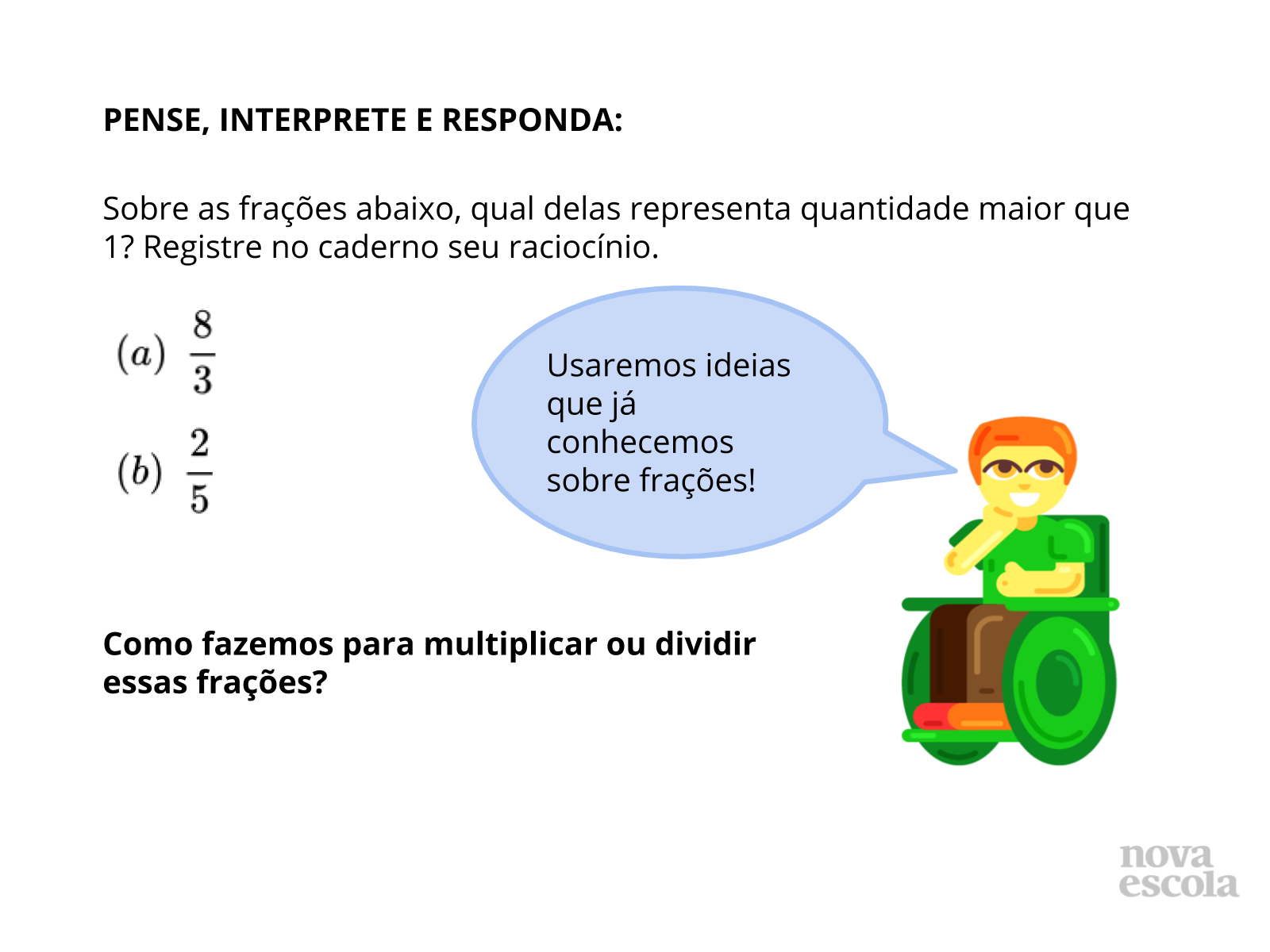
Orientações: Organize os alunos em duplas, de modo que não fiquem de costas uns para os outros, pois haverá momentos de discussões e socialização das soluções. Leia para a turma o enunciado, esclareça possíveis dúvidas e sugira que pensem, junto com o colega de dupla, em uma forma de chegar em uma resposta. Dê um tempo de 2 minutos para essa discussão. Antes de projetar os slides seguintes, verifique se alguém quer compartilhar sua resposta. Só então, se achar necessário, projete os slides 4 e 5 com uma forma de abordagem para o problema.
Essa atividade permite também que você verifique se os alunos se lembram das operações que serão utilizadas na atividade seguinte. Caso algum aluno não se lembre dos algoritmos da multiplicação e da divisão de decimais, peça a um colega que explique, dando alguns exemplos.
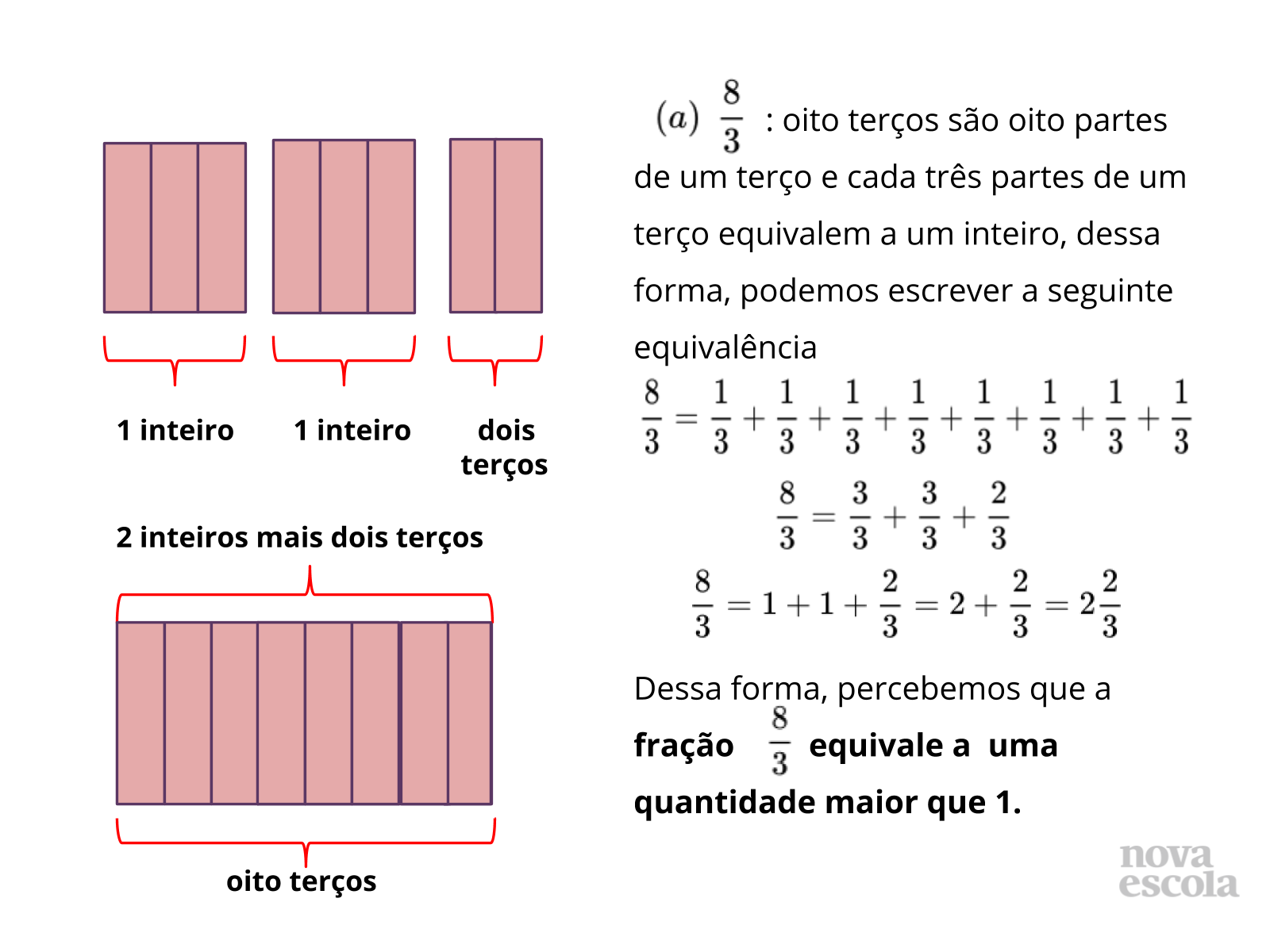
Propósito: Retomar os conceitos de fração própria, fração imprópria e número misto, analisar visualmente a transformação de uma fração imprópria em número misto e diagnosticar o quanto os alunos se lembram sobre as operações com frações.
Discuta com a Turma:
- Qual a melhor forma de visualizar a quantidade do inteiro que uma fração representa? Para este caso, a notação fracionária ou decimal são as mais indicadas?
- Qual a relação entre numerador e denominador para que o resultado seja maior que 1? E para que seja menor que 1?
- No item (a), transformamos a fração em número misto. Podemos fazer isso com todas as frações?
Materiais Complementares:
Retomada
Tempo sugerido: 6 minutos (slides 3, 4 e 5)
Orientações: Organize os alunos em duplas, de modo que não fiquem de costas uns para os outros, pois haverá momentos de discussões e socialização das soluções. Leia para a turma o enunciado, esclareça possíveis dúvidas e sugira que pensem, junto com o colega de dupla, em uma forma de chegar em uma resposta. Dê um tempo de 2 minutos para essa discussão. Antes de projetar os slides seguintes, verifique se alguém quer compartilhar sua resposta. Só então, se achar necessário, projete os slides 4 e 5 com uma forma de abordagem para o problema.
Essa atividade permite também que você verifique se os alunos se lembram das operações que serão utilizadas na atividade seguinte. Caso algum aluno não se lembre dos algoritmos da multiplicação e da divisão de decimais, peça a um colega que explique, dando alguns exemplos.
Propósito: Retomar os conceitos de fração própria, fração imprópria e número misto, analisar visualmente a transformação de uma fração imprópria em número misto e diagnosticar o quanto os alunos se lembram sobre as operações com frações.
Discuta com a Turma:
- Qual a melhor forma de visualizar a quantidade do inteiro que uma fração representa? Para este caso, a notação fracionária ou decimal são as mais indicadas?
- Qual a relação entre numerador e denominador para que o resultado seja maior que 1? E para que seja menor que 1?
- No item (a), transformamos a fração em número misto. Podemos fazer isso com todas as frações?
Retomada
Tempo sugerido: 6 minutos (slides 3, 4 e 5)
Orientações: Organize os alunos em duplas, de modo que não fiquem de costas uns para os outros, pois haverá momentos de discussões e socialização das soluções. Leia para a turma o enunciado, esclareça possíveis dúvidas e sugira que pensem, junto com o colega de dupla, em uma forma de chegar em uma resposta. Dê um tempo de 2 minutos para essa discussão. Antes de projetar os slides seguintes, verifique se alguém quer compartilhar sua resposta. Só então, se achar necessário, projete os slides 4 e 5 com uma forma de abordagem para o problema.
Essa atividade permite também que você verifique se os alunos se lembram das operações que serão utilizadas na atividade seguinte. Caso algum aluno não se lembre dos algoritmos da multiplicação e da divisão de decimais, peça a um colega que explique, dando alguns exemplos.
Propósito: Retomar os conceitos de fração própria, fração imprópria e número misto, analisar visualmente a transformação de uma fração imprópria em número misto e diagnosticar o quanto os alunos se lembram sobre as operações com frações.
Discuta com a Turma:
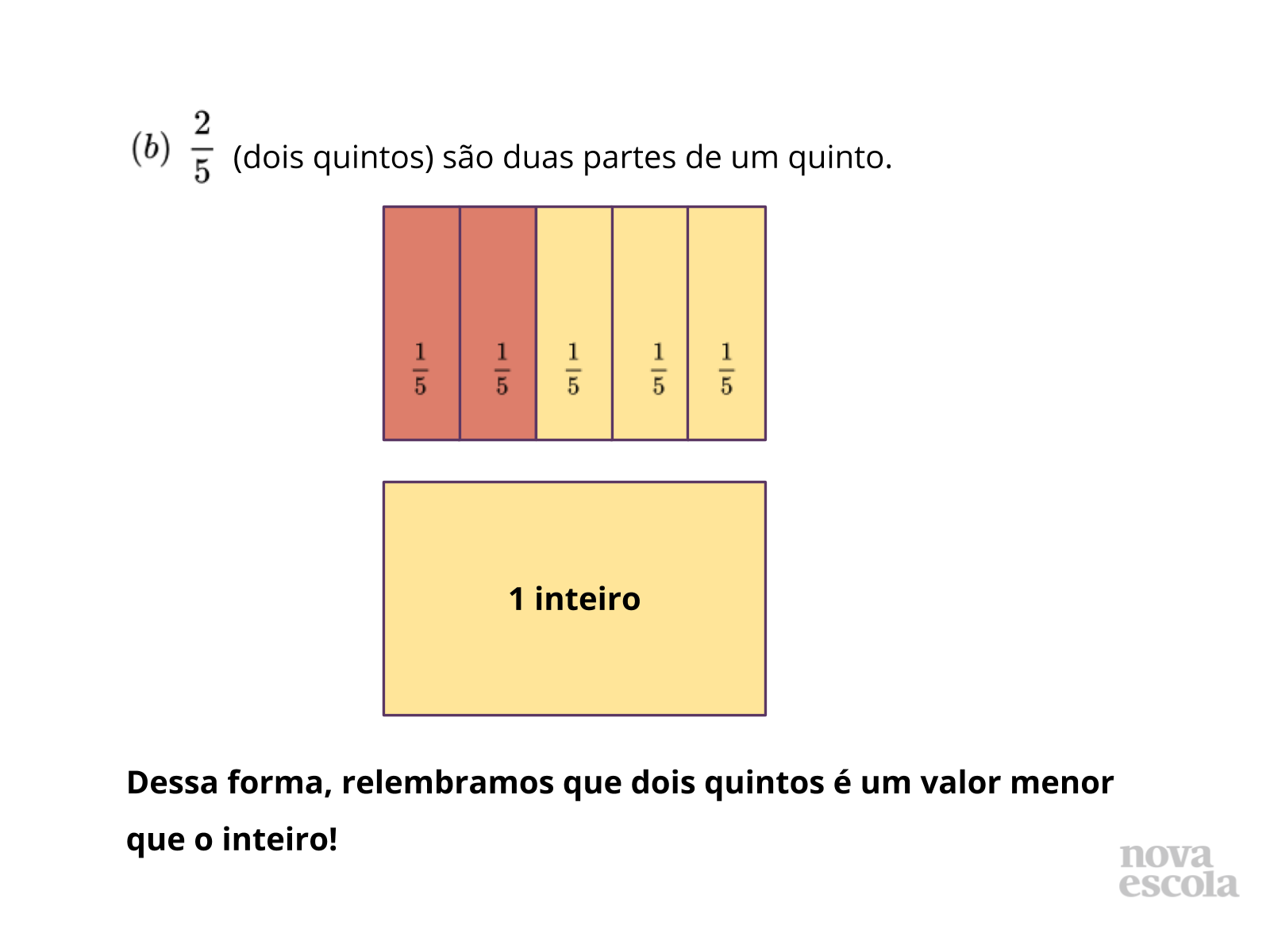
- Qual a melhor forma de visualizar a quantidade do inteiro que uma fração representa? Para este caso, a notação fracionária ou decimal são as mais indicadas?
- Qual a relação entre numerador e denominador para que o resultado seja maior que 1? E para que seja menor que 1?
- No item (a), transformamos a fração em número misto. Podemos fazer isso com todas as frações?
Atividade Principal

Tempo sugerido: 15 minutos (Slides 6 a 8)
Orientações: Projete o slide, leia o enunciado ou, se preferir, entregue uma cópia impressa da atividade aos alunos e esclareça possíveis dúvidas. Peça para tentarem iniciar a resolução sozinhos por 2 minutos, após esse tempo, libere-os para discutir e concluir suas soluções com o colega de dupla. Sugira que tentem solucionar buscando uma forma visual de representar o problema. Circule pela sala de aula mediando as discussões para garantir o entendimento e a participação de todos. Esclareça dúvidas e auxilie no processo de resolução consultando o Guia de Intervenções. Neste momento, é importante que você deixe que eles confrontem suas opiniões para aprender a aceitar e valorizar ideias e raciocínios diferentes dos seus.
Propósito: Apresentar o enunciado e passar as instruções para resolver a Atividade Principal.
Discuta com a Turma:
- Para resolver um exercício, devemos ter em mente o que o problema está pedindo, você consegue anotar ou destacar essas informações no texto?
- Quais são as informações relevantes do enunciado? Anote.
- Você consegue pensar em uma estratégia para resolver este problema?
Materiais complementares para impressão:
Atividade Principal

Tempo sugerido: 15 minutos (Slides 6 a 8)
Orientações: Projete o slide, leia o enunciado ou, se preferir, entregue uma cópia impressa da atividade aos alunos e esclareça possíveis dúvidas. Peça para tentarem iniciar a resolução sozinhos por 2 minutos, após esse tempo, libere-os para discutir e concluir suas soluções com o colega de dupla. Sugira que tentem solucionar buscando uma forma visual de representar o problema. Circule pela sala de aula mediando as discussões para garantir o entendimento e a participação de todos. Esclareça dúvidas e auxilie no processo de resolução consultando o Guia de Intervenções. Neste momento, é importante que você deixe que eles confrontem suas opiniões para aprender a aceitar e valorizar ideias e raciocínios diferentes dos seus.
Propósito: Apresentar o enunciado e passar as instruções para resolver a Atividade Principal.
Discuta com a Turma:
- Para resolver um exercício, devemos ter em mente o que o problema está pedindo, você consegue anotar ou destacar essas informações no texto?
- Quais são as informações relevantes do enunciado? Anote.
- Você consegue pensar em uma estratégia para resolver este problema?
Atividade Principal

Tempo sugerido: 15 minutos (Slides 6 a 8)
Orientações: Projete o slide, leia o enunciado ou, se preferir, entregue uma cópia impressa da atividade aos alunos e esclareça possíveis dúvidas. Peça para tentarem iniciar a resolução sozinhos por 2 minutos, após esse tempo, libere-os para discutir e concluir suas soluções com o colega de dupla. Sugira que tentem solucionar buscando uma forma visual de representar o problema. Circule pela sala de aula mediando as discussões para garantir o entendimento e a participação de todos. Esclareça dúvidas e auxilie no processo de resolução consultando o Guia de Intervenções. Neste momento, é importante que você deixe que eles confrontem suas opiniões para aprender a aceitar e valorizar ideias e raciocínios diferentes dos seus.
Propósito: Apresentar o enunciado e passar as instruções para resolver a Atividade Principal.
Discuta com a Turma:
- Para resolver um exercício, devemos ter em mente o que o problema está pedindo, você consegue anotar ou destacar essas informações no texto?
- Quais são as informações relevantes do enunciado? Anote.
- Você consegue pensar em uma estratégia para resolver este problema?
Discussão das Soluções

Tempo sugerido: 15 minutos. (slides 9 a 16)
Orientações: Convide os alunos a irem ao quadro apresentar suas soluções, incentivando e mediando a discussão sobre as diferentes soluções construídas. Somente ao final dessa discussão, projete o slide com a interpretação visual da solução. Ao mostrar o slide 9, verifique se eles compreendem a forma como a imagem foi construída, fazendo algumas perguntas, como as que aparecem abaixo. Se julgar necessário, peça a um aluno que explique por que um terço de nove meios é três meios utilizando a imagem. Peça também que tentem seguir esse caminho da representação visual para atingir a resposta do problema. Só então exiba os slides seguintes.
Propósito: Debater as soluções encontradas pelos alunos e apresentar uma solução voltada para a interpretação visual de frações.
Discuta com a Turma:
- Alguém encontrou outra forma de representar visualmente a situação?
- Por que um terço de nove meios é três meios?
- Ao multiplicar um número por um terço, o produto será aumentado ou reduzido? Por quê?
Discussão das Soluções
Tempo sugerido: 15 minutos. (slides 9 a 16)
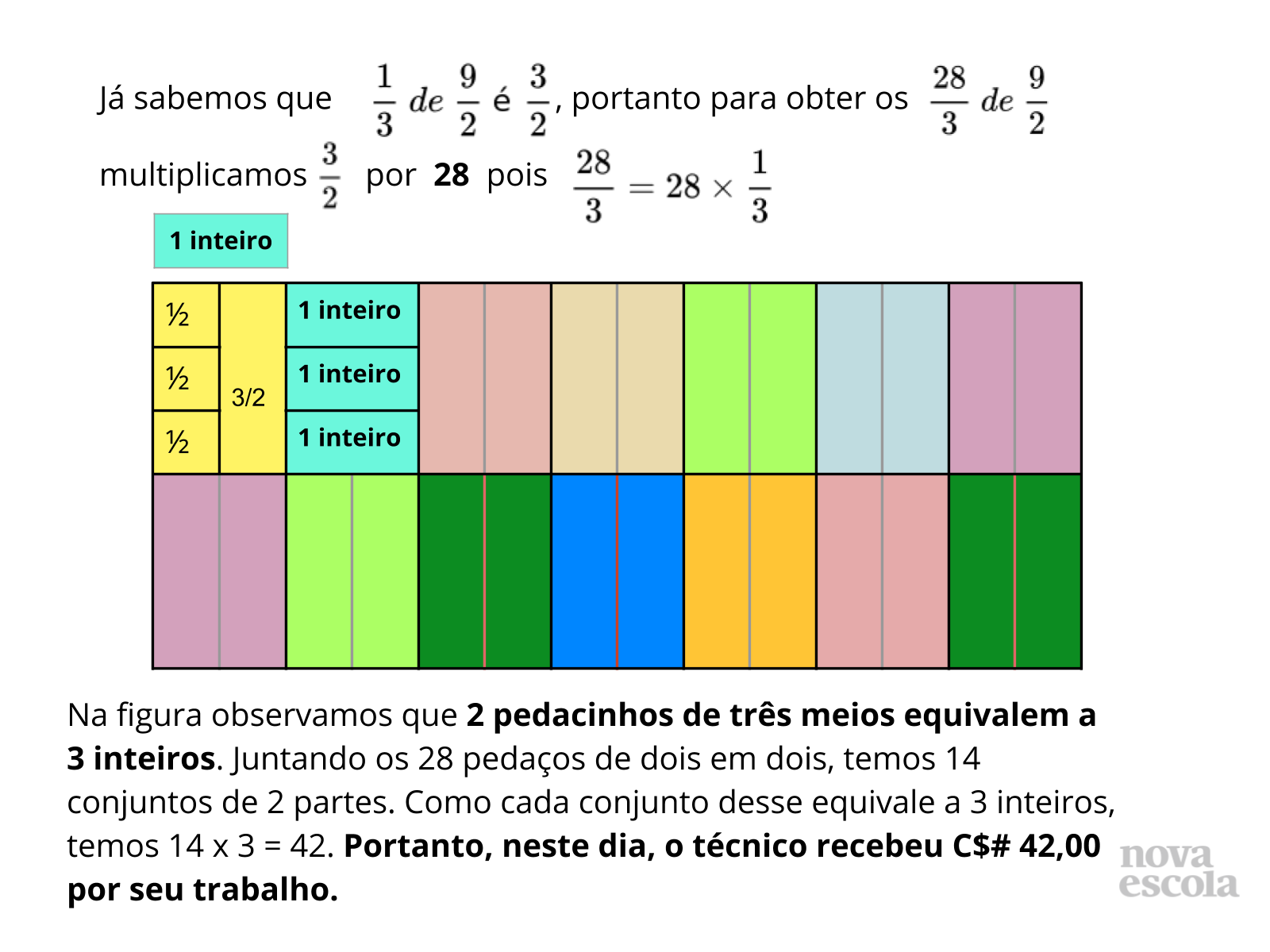
Orientações: Convide os alunos a irem ao quadro apresentar suas soluções, incentivando e mediando a discussão sobre as diferentes soluções construídas. Somente ao final dessa discussão, projete o slide com a interpretação visual da solução. Ao mostrar o slide 9, verifique se eles compreendem a forma como a imagem foi construída, fazendo algumas perguntas, como as que aparecem abaixo. Se julgar necessário, peça a um aluno que explique por que um terço de nove meios é três meios utilizando a imagem. Peça também que tentem seguir esse caminho da representação visual para atingir a resposta do problema. Só então exiba os slides seguintes.
Propósito: Debater as soluções encontradas pelos alunos e apresentar uma solução voltada para a interpretação visual de frações.
Discussão das Soluções
Tempo sugerido: 15 minutos. (slides 9 a 16)
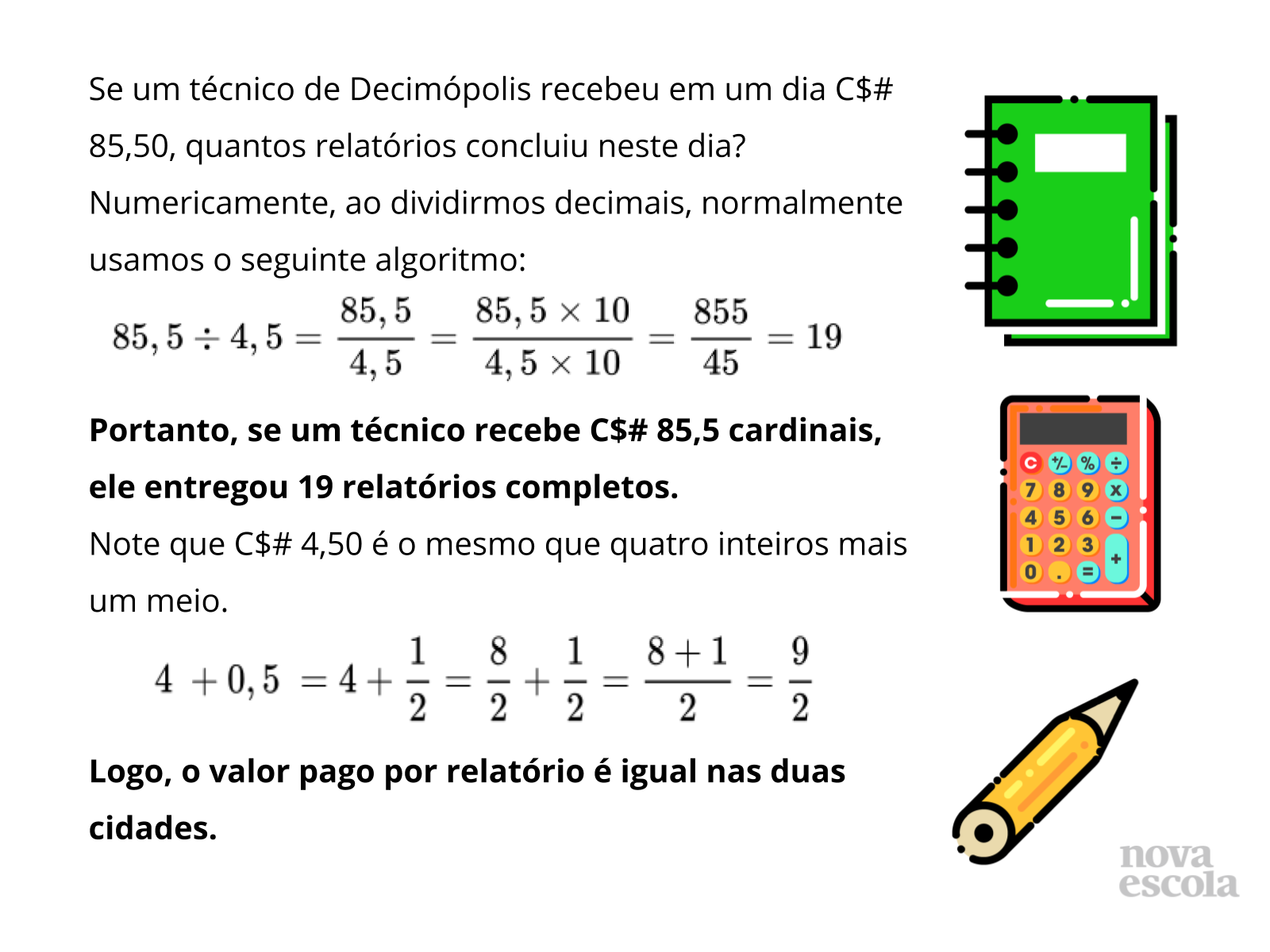
Orientações: Convide os alunos a irem ao quadro apresentar suas soluções, incentivando e mediando a discussão sobre as diferentes soluções construídas. Somente ao final dessa discussão, projete o slide com a interpretação visual da solução. Ao mostrar o slide 9, verifique se eles compreendem a forma como a imagem foi construída, fazendo algumas perguntas, como as que aparecem abaixo. Se julgar necessário, peça a um aluno que explique por que um terço de nove meios é três meios utilizando a imagem. Peça também que tentem seguir esse caminho da representação visual para atingir a resposta do problema. Só então exiba os slides seguintes.
Propósito: Debater as soluções encontradas pelos alunos e apresentar uma solução voltada para a interpretação visual de frações.
Discussão das Soluções

Tempo sugerido: 15 minutos. (slides 9 a 16)
Orientações: Convide os alunos a irem ao quadro apresentar suas soluções, incentivando e mediando a discussão sobre as diferentes soluções construídas. Somente ao final dessa discussão, projete o slide com a interpretação visual da solução. Ao mostrar o slide 9, verifique se eles compreendem a forma como a imagem foi construída, fazendo algumas perguntas, como as que aparecem abaixo. Se julgar necessário, peça a um aluno que explique por que um terço de nove meios é três meios utilizando a imagem. Peça também que tentem seguir esse caminho da representação visual para atingir a resposta do problema. Só então exiba os slides seguintes.
Propósito: Debater as soluções encontradas pelos alunos e apresentar uma solução voltada para a interpretação visual de frações.
Discussão das Soluções

Tempo sugerido: 15 minutos. (slides 9 a 16)
Orientações: Convide os alunos a irem ao quadro apresentar suas soluções, incentivando e mediando a discussão sobre as diferentes soluções construídas. Somente ao final dessa discussão, projete o slide com a interpretação visual da solução. Ao mostrar o slide 9, verifique se eles compreendem a forma como a imagem foi construída, fazendo algumas perguntas, como as que aparecem abaixo. Se julgar necessário, peça a um aluno que explique por que um terço de nove meios é três meios utilizando a imagem. Peça também que tentem seguir esse caminho da representação visual para atingir a resposta do problema. Só então exiba os slides seguintes.
Propósito: Debater as soluções encontradas pelos alunos e apresentar uma solução voltada para a interpretação visual de frações.
Discussão das Soluções
Tempo sugerido: 15 minutos. (slides 9 a 16)
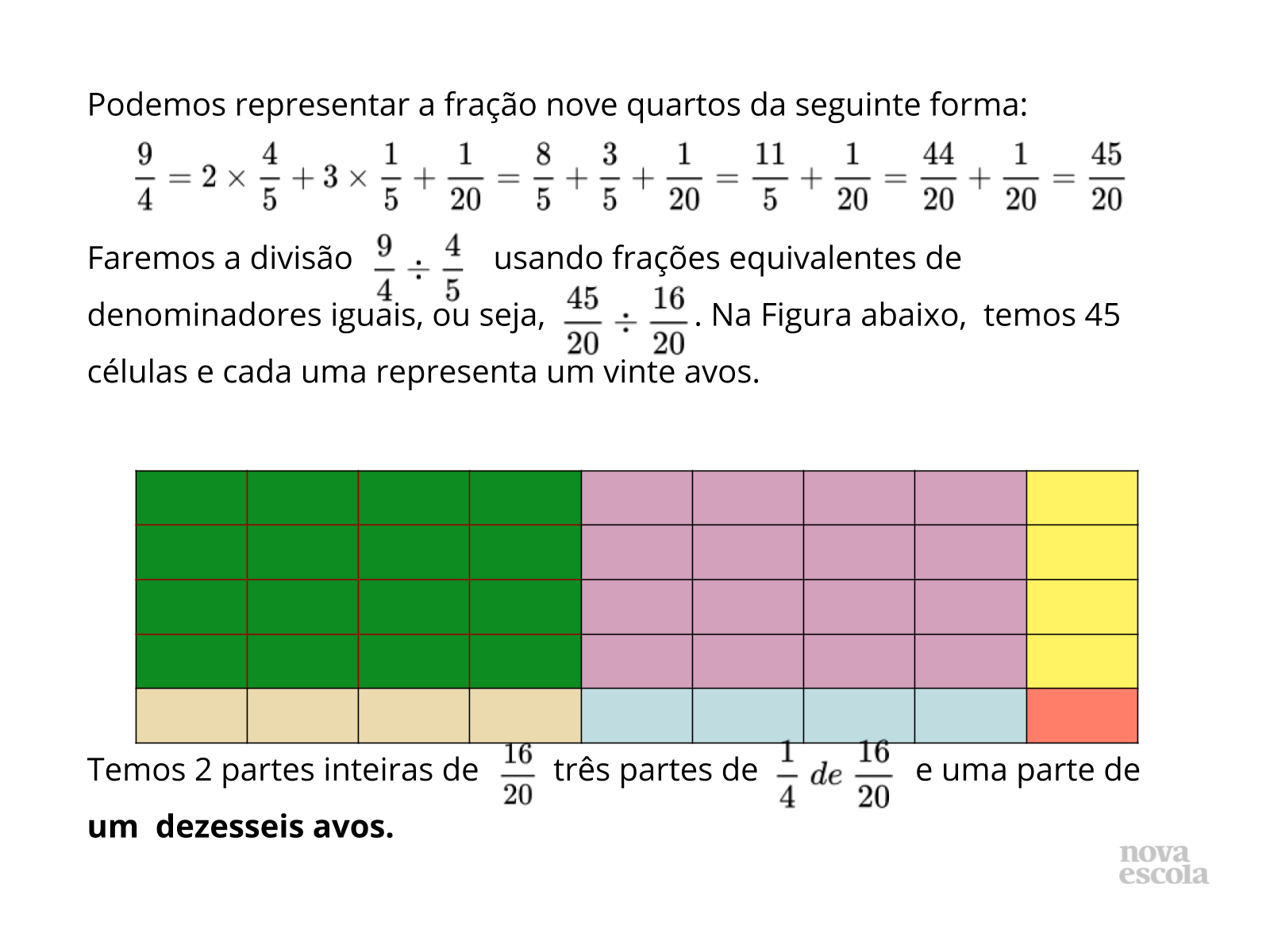
Orientações: Convide os alunos a irem ao quadro apresentar suas soluções, incentivando e mediando a discussão sobre as diferentes soluções construídas. Somente ao final dessa discussão, projete o slide com a interpretação visual da solução. Ao mostrar o slide 9, verifique se eles compreendem a forma como a imagem foi construída, fazendo algumas perguntas, como as que aparecem abaixo. Se julgar necessário, peça a um aluno que explique por que um terço de nove meios é três meios utilizando a imagem. Peça também que tentem seguir esse caminho da representação visual para atingir a resposta do problema. Só então exiba os slides seguintes.
Propósito: Debater as soluções encontradas pelos alunos e apresentar uma solução voltada para a interpretação visual de frações.
Discuta com a Turma:
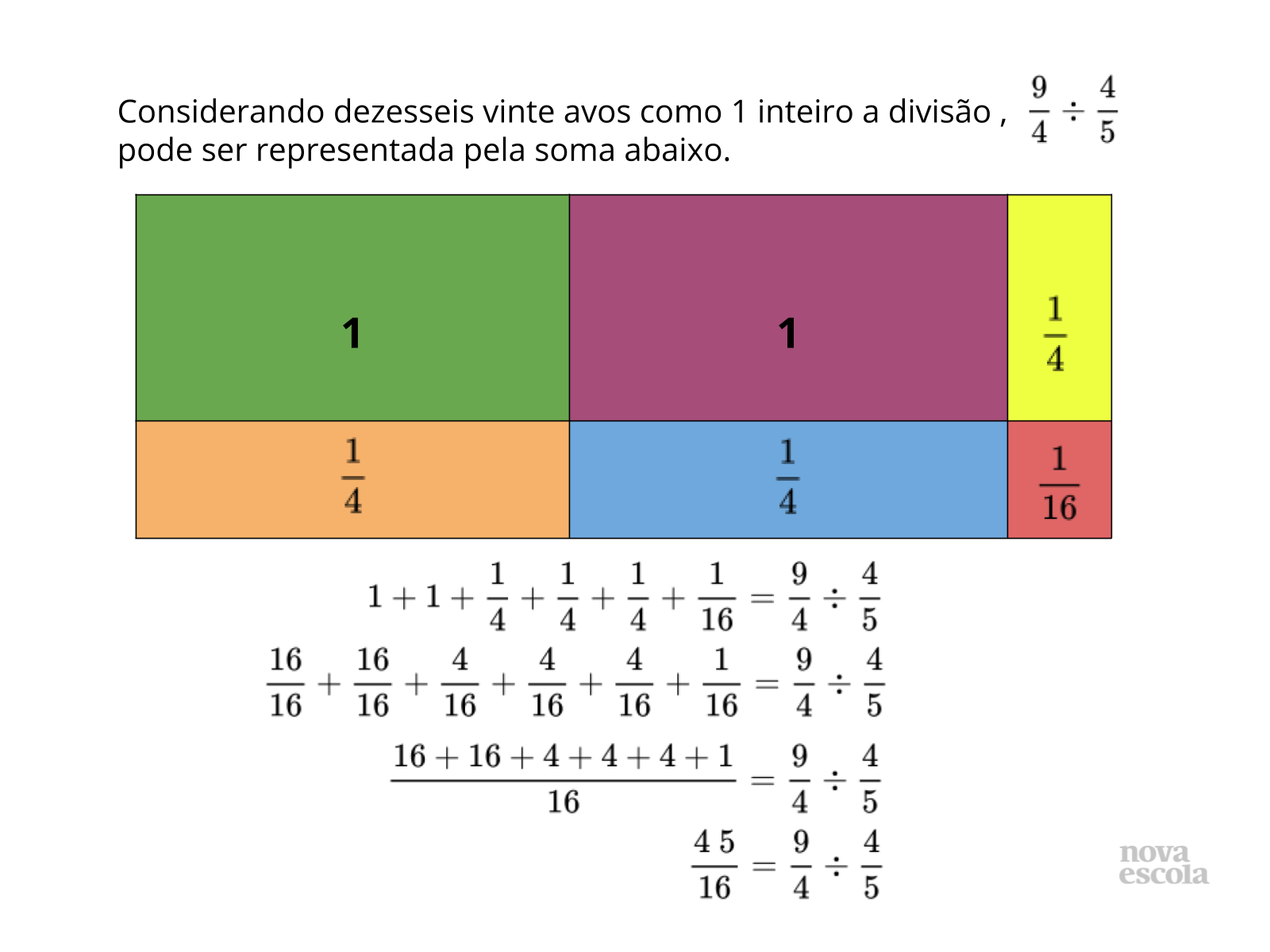
- Precisamos dividir quarenta e cinco dezesseis avos por dezesseis vinte avos, ou seja, quantas partes de dezesseis vinte avos podemos obter?
Discussão das Soluções
Tempo sugerido: 15 minutos. (slides 9 a 16)
Orientações: Convide os alunos a irem ao quadro apresentar suas soluções, incentivando e mediando a discussão sobre as diferentes soluções construídas. Somente ao final dessa discussão, projete o slide com a interpretação visual da solução. Ao mostrar o slide 9, verifique se eles compreendem a forma como a imagem foi construída, fazendo algumas perguntas, como as que aparecem abaixo. Se julgar necessário, peça a um aluno que explique por que um terço de nove meios é três meios utilizando a imagem. Peça também que tentem seguir esse caminho da representação visual para atingir a resposta do problema. Só então exiba os slides seguintes.
Propósito: Debater as soluções encontradas pelos alunos e apresentar uma solução voltada para a interpretação visual de frações.
Discuta com a Turma:
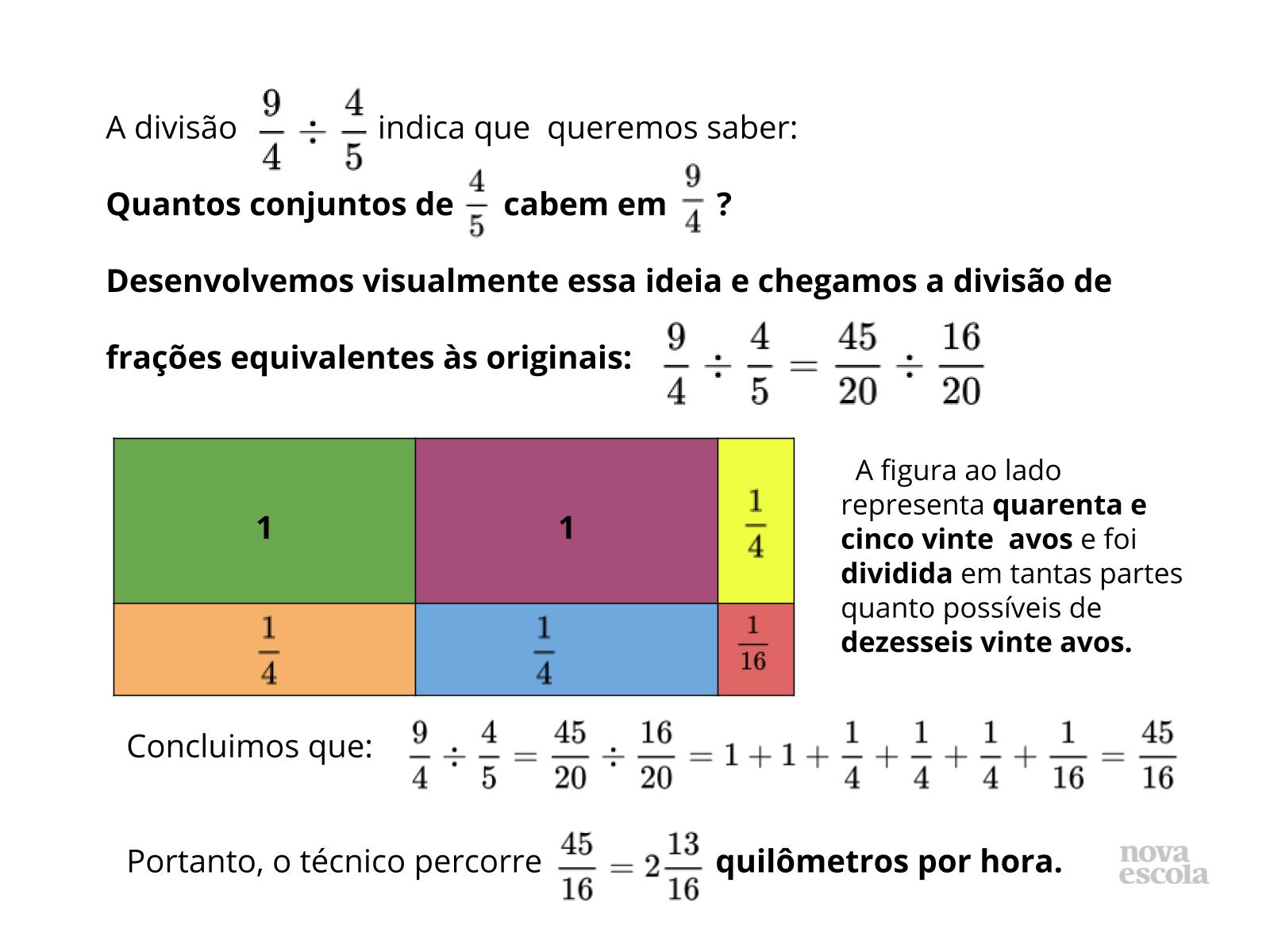
- As partes de um vinte avos do todo são equivalentes às partes de 1 dezesseis avos do divisor?
Discussão das Soluções
Tempo sugerido: 15 minutos. (slides 9 a 16)
Orientações: Convide os alunos a irem ao quadro apresentar suas soluções, incentivando e mediando a discussão sobre as diferentes soluções construídas. Somente ao final dessa discussão, projete o slide com a interpretação visual da solução. Ao mostrar o slide 9, verifique se eles compreendem a forma como a imagem foi construída, fazendo algumas perguntas, como as que aparecem abaixo. Se julgar necessário, peça a um aluno que explique por que um terço de nove meios é três meios utilizando a imagem. Peça também que tentem seguir esse caminho da representação visual para atingir a resposta do problema. Só então exiba os slides seguintes.
Propósito: Debater as soluções encontradas pelos alunos e apresentar uma solução voltada para a interpretação visual de frações.
Discuta com a Turma:
- Quantas vezes o divisor cabe dentro do dividendo?
Encerramento
Tempo sugerido: 4 minutos (slides 17 e 18)
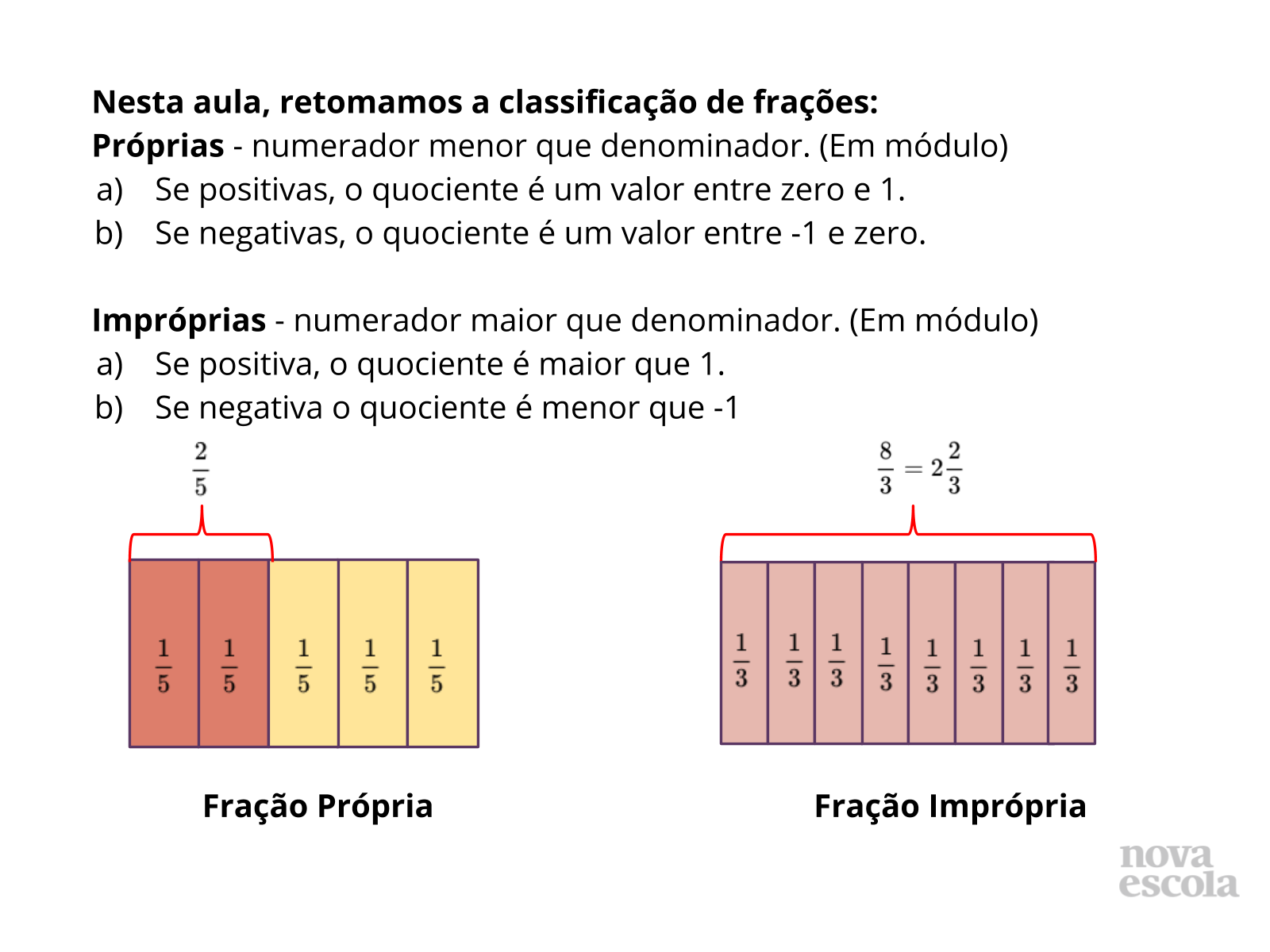
Orientações: Finalizar a aula com a exposição deste slide e do próximo, antecedendo a Atividade Raio X. Verifique se ainda há dúvidas entre os alunos antes de aplicar o Raio X.
Propósito: Revisar os tópicos mais importantes dos conteúdos desenvolvidos na aula e esclarecer as dúvidas da turma antes do momento de avaliação.
Encerramento

Tempo sugerido: 4 minutos (slides 17 e 18)
Orientações: Finalizar a aula com a exposição deste slide e do próximo, antecedendo a Atividade Raio X. Verifique se ainda há dúvidas entre os alunos antes de aplicar o Raio X.
Propósito: Revisar os tópicos mais importantes dos conteúdos desenvolvidos na aula e esclarecer as dúvidas da turma antes do momento de avaliação.
Raio X

Tempo sugerido: 8 minutos.
Orientações: Ler a proposta junto com os alunos, verificar se todos compreenderam o problema e sabem o que devem fazer. Peça para que resolvam a ativdade. Circule pela sala para verificar as resoluções. Lembre-se que neste momento, você está avaliando os avanços dos estudantes em relação ao conteúdo da aula. Procure identificar as dúvidas que ainda ficaram e reserve os minutos finais da aula para uma breve correção desta atividade. Nos 3 minutos finais, peça para os estudantes comparar suas respostas com as respostas dos colegas para verificarem seus erros e acertos.
Propósito: Verificar a assimilação dos conteúdos expostos durante a aula.
Materiais Complementares:
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
( a definir) .Cálculo das quatro operações e potenciação com números inteiros e racionais (fluência em cálculo mental; escrito e aproximado ou calculadora)
Objetivos Específicos
Resolver e interpretar problemas aplicando as operações de adição, subtração, multiplicação e divisão de racionais nas formas fracionária e decimal.
Conceito-chave
Fração, número decimal, multiplicação, divisão.
Recursos Necessários
- Projetor (caso haja)
- Calculadoras;
- Atividades impressas em folhas, coladas no caderno ou não.