Retomada
Plano de Aula
Plano de aula: Número é Número, Não Importa como está Escrito!
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Operações aritméticas com números inteiros e racionais
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Objetivos Específicos
Interpretar e resolver problemas visualmente e numericamente com números racionais na forma decimal e fracionária, aplicando as operações de adição e subtração.
Conceito-chave
Fração, número decimal, operações de adição e subtração.
Recursos Necessários
- Projetor (caso haja)
- Calculadoras
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Objetivos Específicos
Interpretar e resolver problemas visualmente e numericamente com números racionais na forma decimal e fracionária, aplicando as operações de adição e subtração.
Conceito-chave
Fração, número decimal, operações de adição e subtração.
Recursos Necessários
- Projetor (caso haja)
- Calculadoras
- Atividades impressas em folhas, coladas no caderno ou não.
Resumo da aula
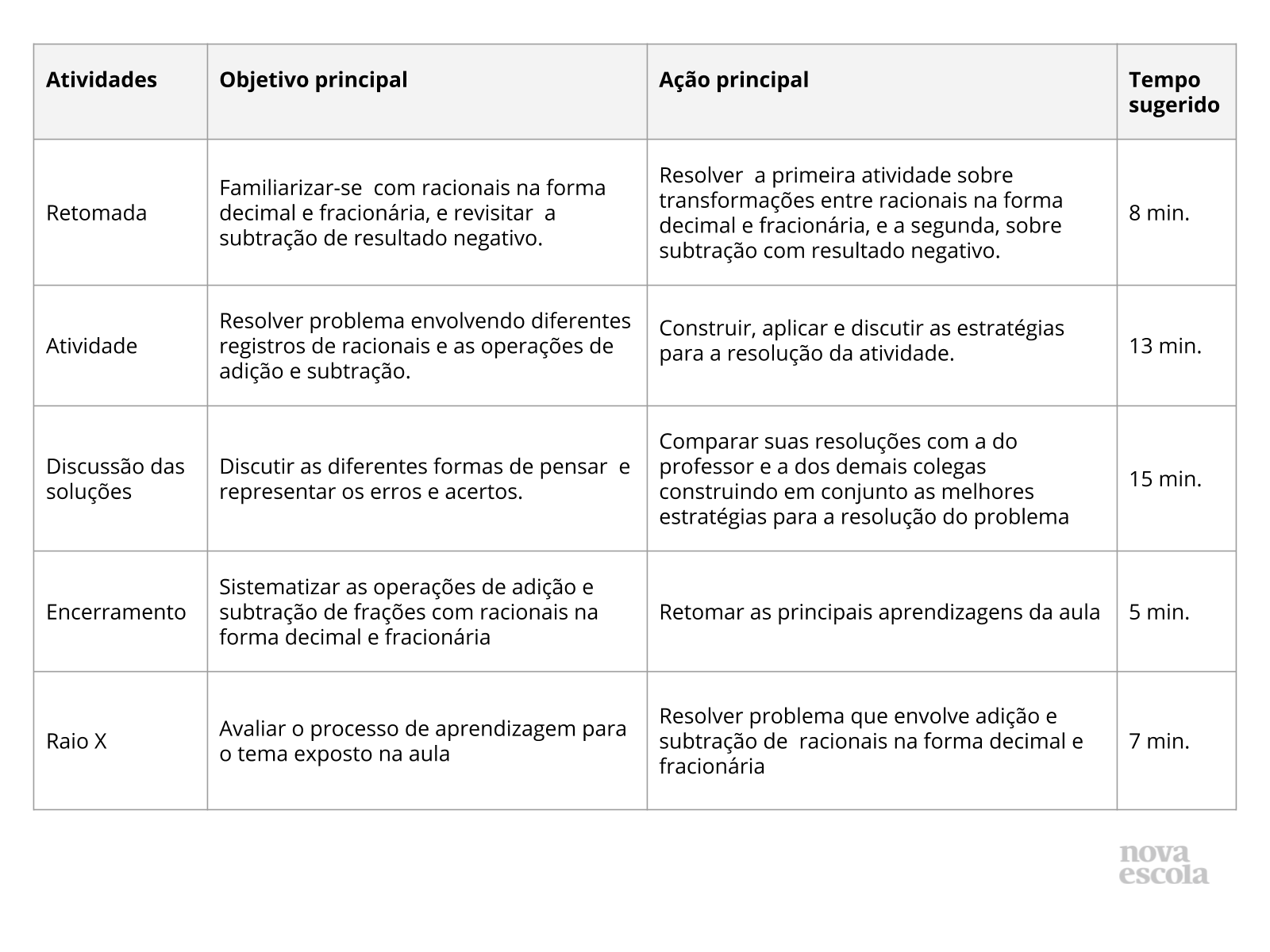
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo Sugerido: 8 minutos. (slides 3 a 5)
Orientações: Leia o enunciado do slide 3 com a classe e deixe os alunos pensarem em como resolver. Em seguida, apresente a resolução mostrando a divisão entre 2 e 5 usando o algoritmo convencional. Peça para os alunos confirmarem usando a calculadora.
Em seguida mostre a representação visual de 2 ÷ 5 no slide 4. Enfatize a soma de frações com denominadores iguais e também o algoritmo para a soma de decimais. Ainda no slide 4, desenvolva a ideia de relação entre os dois tipos de registro (decimal e fracionário), mostrando aos alunos que a soma de duas partes resulta em dois quintos ou 0,4, quando dividimos o numerador pelo denominador, reforçando a ideia de que ambas as representações significam a mesma quantidade.
Para finalizar essa atividade, proponha a questão dada no slide 5. Leia o enunciado com a classe e peça para que eles pensem em como resolver. Mostre que podemos calcular usando frações, pois 0,4 equivale a quatro décimos (ou seja ,quatro sobre dez). Compare as duas frações e faça com que percebam que nove quartos é maior que quatro décimos, portanto, o resultado é negativo. Outra possibilidade é transformar nove quartos em número decimal e efetuar a subtração. Comente que não é muito comum vermos nos livros dessa série, mas existem números decimais negativos.
Propósito: Relembrar conceitos que já foram trabalhados em unidades anteriores e fornecer ferramentas para que os estudantes possam trabalhar na resolução da atividade principal.
Discuta com a turma:
- Quais são as equivalências entre frações e decimais dadas nestas atividades?
- Por que a figura do slide foi dividida em 5 partes iguais? Pense no conceito de denominador e numerador de uma fração.
- Por que tiramos o MMC dos denominadores quando somamos frações?
- Vocês podem dar exemplos de situações que sejam representadas por decimais negativos?
Materiais complementares:
Retomada

Tempo Sugerido: 8 minutos. (slides 3 a 5)
Orientações: Leia o enunciado do slide 3 com a classe e deixe os alunos pensarem em como resolver. Em seguida, apresente a resolução mostrando a divisão entre 2 e 5 usando o algoritmo convencional. Peça para os alunos confirmarem usando a calculadora.
Em seguida mostre a representação visual de 2 ÷ 5 no slide 4. Enfatize a soma de frações com denominadores iguais e também o algoritmo para a soma de decimais. Ainda no slide 4, desenvolva a ideia de relação entre os dois tipos de registro (decimal e fracionário), mostrando aos alunos que a soma de duas partes resulta em dois quintos ou 0,4, quando dividimos o numerador pelo denominador, reforçando a ideia de que ambas as representações significam a mesma quantidade.
Para finalizar essa atividade, proponha a questão dada no slide 5. Leia o enunciado com a classe e peça para que eles pensem em como resolver. Mostre que podemos calcular usando frações, pois 0,4 equivale a quatro décimos (ou seja ,quatro sobre dez). Compare as duas frações e faça com que percebam que nove quartos é maior que quatro décimos, portanto, o resultado é negativo. Outra possibilidade é transformar nove quartos em número decimal e efetuar a subtração. Comente que não é muito comum vermos nos livros dessa série, mas existem números decimais negativos.
Propósito: Relembrar conceitos que já foram trabalhados em unidades anteriores e fornecer ferramentas para que os estudantes possam trabalhar na resolução da atividade principal.
Discuta com a turma:
- Quais são as equivalências entre frações e decimais dadas nestas atividades?
- Por que a figura do slide foi dividida em 5 partes iguais? Pense no conceito de denominador e numerador de uma fração.
- Por que tiramos o MMC dos denominadores quando somamos frações?
- Vocês podem dar exemplos de situações que sejam representadas por decimais negativos?
Retomada

Tempo Sugerido: 8 minutos. (slides 3 a 5)
Orientações: Leia o enunciado do slide 3 com a classe e deixe os alunos pensarem em como resolver. Em seguida, apresente a resolução mostrando a divisão entre 2 e 5 usando o algoritmo convencional. Peça para os alunos confirmarem usando a calculadora.
Em seguida mostre a representação visual de 2 ÷ 5 no slide 4. Enfatize a soma de frações com denominadores iguais e também o algoritmo para a soma de decimais. Ainda no slide 4, desenvolva a ideia de relação entre os dois tipos de registro (decimal e fracionário), mostrando aos alunos que a soma de duas partes resulta em dois quintos ou 0,4, quando dividimos o numerador pelo denominador, reforçando a ideia de que ambas as representações significam a mesma quantidade.
Para finalizar essa atividade, proponha a questão dada no slide 5. Leia o enunciado com a classe e peça para que eles pensem em como resolver. Mostre que podemos calcular usando frações, pois 0,4 equivale a quatro décimos (ou seja ,quatro sobre dez). Compare as duas frações e faça com que percebam que nove quartos é maior que quatro décimos, portanto, o resultado é negativo. Outra possibilidade é transformar nove quartos em número decimal e efetuar a subtração. Comente que não é muito comum vermos nos livros dessa série, mas existem números decimais negativos.
Propósito: Relembrar conceitos que já foram trabalhados em unidades anteriores e fornecer ferramentas para que os estudantes possam trabalhar na resolução da atividade principal.
Discuta com a turma:
- Quais são as equivalências entre frações e decimais dadas nestas atividades?
- Por que a figura do slide foi dividida em 5 partes iguais? Pense no conceito de denominador e numerador de uma fração.
- Por que tiramos o MMC dos denominadores quando somamos frações?
- Vocês podem dar exemplos de situações que sejam representadas por decimais negativos?
Atividade Principal

Tempo sugerido: 10 minutos. (Slides 6 e 7)
Orientação: Discuta o texto do slide 6 e atente para as dúvidas dos estudantes, pois as próximas etapas da aula dependem muito da assimilação dos conceitos trabalhados nas duas atividades de retomada. Distribua os enunciados da atividade principal impressa e/ou projete o slide 7. Peça que, individualmente, que os alunos leiam a atividade e comecem a resolver por 2 minutos, em silêncio. Após passar esse tempo, libere para discutir as idéias e terminar a resolução em dupla, utilizando qualquer estratégia. O primeiro momento de leitura e início da resolução de forma individual faz com que cada um tenha suas próprias idéias para poder discutir com seu companheiro de equipe.
Propósito: Desenvolver o raciocínio voltado para a leitura, interpretação e resolução de um problema que exija alta demanda cognitiva através do esforço produtivo e colaborativo.
Discuta com a turma:
- Alguém gostaria de socializar uma forma diferente de resolver a atividade?
- Para resolvermos um problema, devemos ter em mente:
(A)Procurar entender o que problema está pedindo para fazer, você até anotar ou destacar no texto;
(B) Verificar quais são as informações relevantes do enunciado e anotar;
(C) Pensar em uma estratégia para resolver;
(D) Colocar em prática o que pensou.
Materiais Complementares:
Atividade Principal

Tempo sugerido: 13 minutos. (Slides 6 e 7)
Orientação: Discuta o texto do slide 6 e atente para as dúvidas dos estudantes, pois as próximas etapas da aula dependem muito da assimilação dos conceitos trabalhados nas duas atividades de retomada. Distribua os enunciados da atividade principal impressa e/ou projete o slide 7. Peça que, individualmente, que os alunos leiam a atividade e comecem a resolver por 2 minutos, em silêncio. Após passar esse tempo, libere para discutir as idéias e terminar a resolução em dupla, utilizando qualquer estratégia. O primeiro momento de leitura e início da resolução de forma individual faz com que cada um tenha suas próprias idéias para poder discutir com seu companheiro de equipe.
Enquanto os alunos resolvem e discutem a atividade, circule pela sala e observe as estratégias de resolução de cada um. Se algum aluno apresentar dúvidas ou dificuldades durante a resolução, não forneça a resposta pronta da atividade a ele, busque fazer questionamentos que o ajude a pensar matematicamente e encontrar a resposta desejada.
Propósito: Desenvolver o raciocínio voltado para a leitura, interpretação e resolução de um problema que exija alta demanda cognitiva através do esforço produtivo e colaborativo.
Discuta com a turma:
- Alguém gostaria de socializar uma forma diferente de resolver a atividade?
- Para resolvermos um problema, devemos ter em mente:
(A)Procurar entender o que problema está pedindo para fazer, você pode até anotar ou destacar no texto;
(B) Verificar quais são as informações relevantes do enunciado e anotar;
(C) Pensar em uma estratégia para resolver;
(D) Colocar em prática o que pensou
Materiais Complementares:
Discussão das Soluções

Tempo sugerido: 15 minutos. (Slides 8 a 14)
Orientação: Inicie fazendo os questionamentos do item “Discuta com a Turma”. Só depois apresente o slide e verifique se algum aluno gostaria de expor seu cálculo no quadro. Caso ninguém consiga escrever seus pensamentos, mostre o slide ou faça essa resolução no quadro, com o auxílio deles, tanto utilizando frações quanto utilizando as representações gráficas. Sempre pergunte se alguém resolveu de maneira diferente e qual estratégia utilizou.
Caso algum aluno tenha usado a calculadora para transformar todas as frações em decimais e efetuar o cálculo, o resultado não será exato, pois ? e 14/15 são dízimas periódicas e terão de ser truncadas ou arredondadas. Discuta porque esse resultado pode ser inconveniente em alguns casos. Os erros devem ser discutidos, entendidos e valorizados, pois são um importante meio para chegar no resultado certo.
Por fim, faça o questionamento do slide 14 aos alunos.
OBSERVAÇÃO: Nos slides 9 a 14, há uma interpretação visual para os dados do problema e a resolução . Se o tempo permitir, apresente as duas soluções, caso contrário, preferimos que o professor dê preferência para a solução visual, no slides 9 a 21.
Propósito: Apresentar uma solução para a atividade principal e demonstrar a necessidade de trabalhar com partes iguais do todo ao se somar ou subtrair frações.
Discuta com a turma:
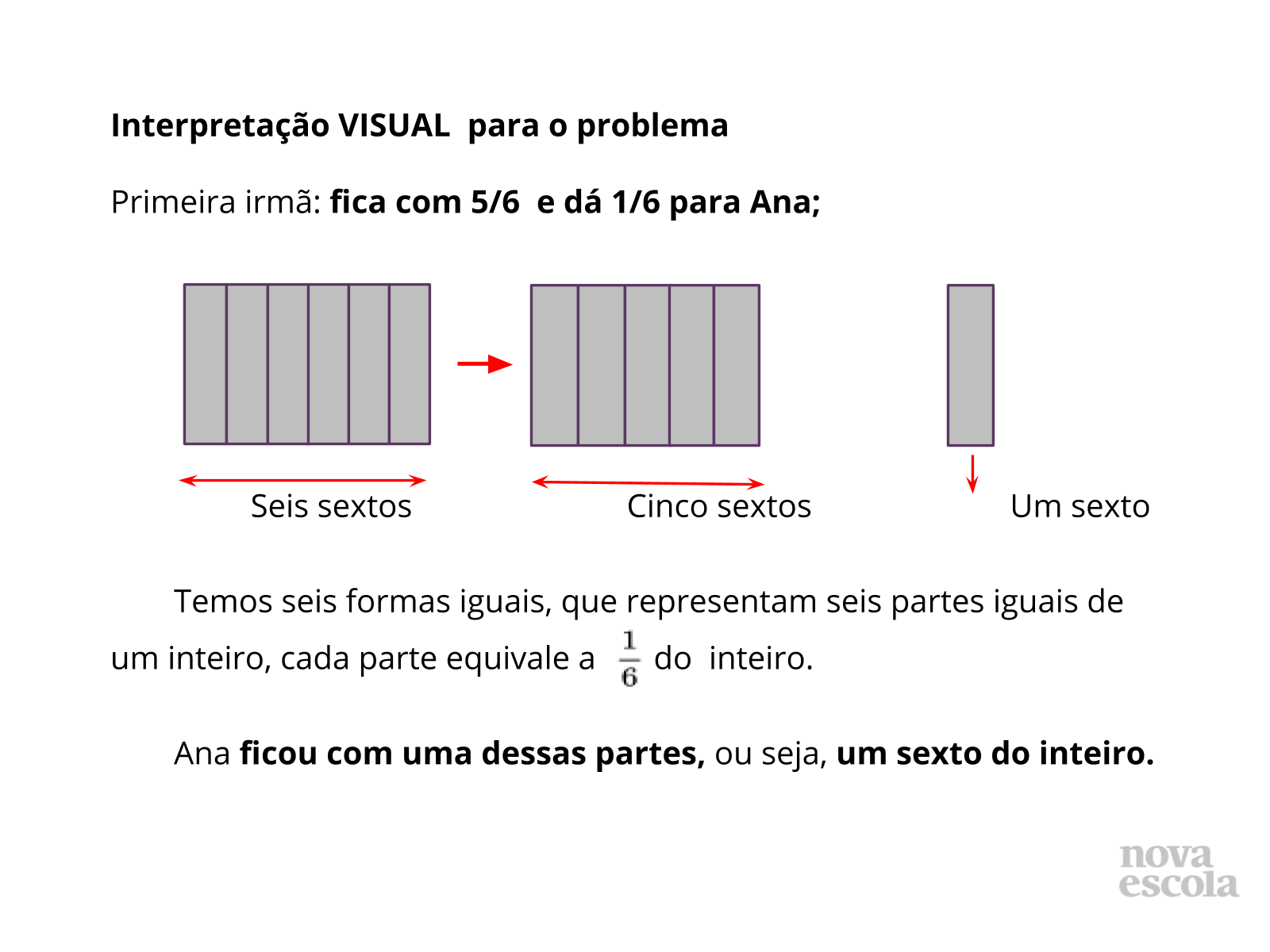
- A primeira irmã fica com 5/6 e dá quanto para Ana?;
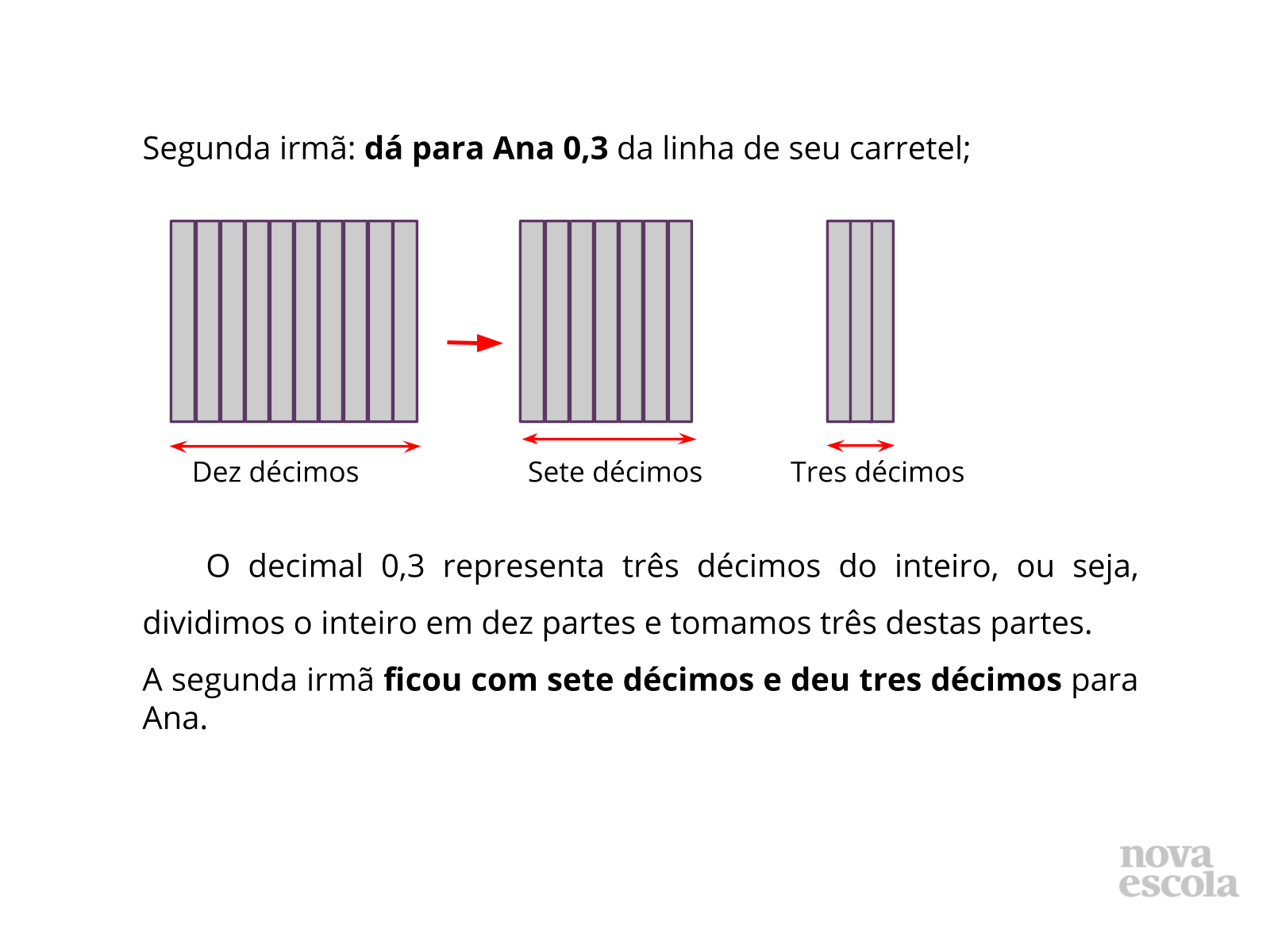
- A segunda irmã dá para Ana 0,3 da linha de seu carretel e fica com quanto?
- A terceira irmã dá a Ana 14/15 da linha de seu carretel e fica com quanto?
Discussão das Soluções
Tempo sugerido: 15 minutos. (Slides 8 a 14)
Orientação: Inicie fazendo os questionamentos do item “Discuta com a Turma”. Só depois apresente o slide e verifique se algum aluno gostaria de expor seu cálculo no quadro. Caso ninguém consiga escrever seus pensamentos, mostre o slide ou faça essa resolução no quadro, com o auxílio deles, tanto utilizando frações quanto utilizando as representações gráficas. Sempre pergunte se alguém resolveu de maneira diferente e qual estratégia utilizou.
Caso algum aluno tenha usado a calculadora para transformar todas as frações em decimais e efetuar o cálculo, o resultado não será exato, pois ? e 14/15 são dízimas periódicas e terão de ser truncadas ou arredondadas. Discuta porque esse resultado pode ser inconveniente em alguns casos. Os erros devem ser discutidos, entendidos e valorizados, pois são um importante meio para chegar no resultado certo.
Por fim, faça o questionamento do slide 14 aos alunos.
OBSERVAÇÃO: Nos slides 9 a 14, há uma interpretação visual para os dados do problema e a resolução . Se o tempo permitir, apresente as duas soluções, caso contrário, preferimos que o professor dê preferência para a solução visual, no slides 9 a 21.
Propósito: Apresentar uma solução para a atividade principal e demonstrar a necessidade de trabalhar com partes iguais do todo ao se somar ou subtrair frações.
Discuta com a turma:
- A primeira irmã fica com 5/6 e dá quanto para Ana?;
- A segunda irmã dá para Ana 0,3 da linha de seu carretel e fica com quanto?
- A terceira irmã dá a Ana 14/15 da linha de seu carretel e fica com quanto?
Discussão das Soluções
Tempo sugerido: 15 minutos. (Slides 8 a 14)
Orientação: Inicie fazendo os questionamentos do item “Discuta com a Turma”. Só depois apresente o slide e verifique se algum aluno gostaria de expor seu cálculo no quadro. Caso ninguém consiga escrever seus pensamentos, mostre o slide ou faça essa resolução no quadro, com o auxílio deles, tanto utilizando frações quanto utilizando as representações gráficas. Sempre pergunte se alguém resolveu de maneira diferente e qual estratégia utilizou.
Caso algum aluno tenha usado a calculadora para transformar todas as frações em decimais e efetuar o cálculo, o resultado não será exato, pois ? e 14/15 são dízimas periódicas e terão de ser truncadas ou arredondadas. Discuta porque esse resultado pode ser inconveniente em alguns casos. Os erros devem ser discutidos, entendidos e valorizados, pois são um importante meio para chegar no resultado certo.
Por fim, faça o questionamento do slide 14 aos alunos.
OBSERVAÇÃO: Nos slides 9 a 14, há uma interpretação visual para os dados do problema e a resolução . Se o tempo permitir, apresente as duas soluções, caso contrário, preferimos que o professor dê preferência para a solução visual, no slides 9 a 21.
Propósito: Apresentar uma solução para a atividade principal e demonstrar a necessidade de trabalhar com partes iguais do todo ao se somar ou subtrair frações.
Discuta com a turma:
- A primeira irmã fica com 5/6 e dá quanto para Ana?;
- A segunda irmã dá para Ana 0,3 da linha de seu carretel e fica com quanto?
- A terceira irmã dá a Ana 14/15 da linha de seu carretel e fica com quanto?
Discussão das Soluções

Tempo sugerido: 15 minutos. (Slides 8 a 14)
Orientação: Inicie fazendo os questionamentos do item “Discuta com a Turma”. Só depois apresente o slide e verifique se algum aluno gostaria de expor seu cálculo no quadro. Caso ninguém consiga escrever seus pensamentos, mostre o slide ou faça essa resolução no quadro, com o auxílio deles, tanto utilizando frações quanto utilizando as representações gráficas. Sempre pergunte se alguém resolveu de maneira diferente e qual estratégia utilizou.
Caso algum aluno tenha usado a calculadora para transformar todas as frações em decimais e efetuar o cálculo, o resultado não será exato, pois ? e 14/15 são dízimas periódicas e terão de ser truncadas ou arredondadas. Discuta porque esse resultado pode ser inconveniente em alguns casos. Os erros devem ser discutidos, entendidos e valorizados, pois são um importante meio para chegar no resultado certo.
Por fim, faça o questionamento do slide 14 aos alunos.
OBSERVAÇÃO: Nos slides 9 a 14, há uma interpretação visual para os dados do problema e a resolução . Se o tempo permitir, apresente as duas soluções, caso contrário, preferimos que o professor dê preferência para a solução visual, no slides 9 a 21.
Propósito: Apresentar uma solução para a atividade principal e demonstrar a necessidade de trabalhar com partes iguais do todo ao se somar ou subtrair frações.
Discuta com a turma:
- A primeira irmã fica com 5/6 e dá quanto para Ana?;
- A segunda irmã dá para Ana 0,3 da linha de seu carretel e fica com quanto?
- A terceira irmã dá a Ana 14/15 da linha de seu carretel e fica com quanto?
Discussão das Soluções
Tempo sugerido: 15 minutos. (Slides 8 a 14)
Orientação: Inicie fazendo os questionamentos do item “Discuta com a Turma”. Só depois apresente o slide e verifique se algum aluno gostaria de expor seu cálculo no quadro. Caso ninguém consiga escrever seus pensamentos, mostre o slide ou faça essa resolução no quadro, com o auxílio deles, tanto utilizando frações quanto utilizando as representações gráficas. Sempre pergunte se alguém resolveu de maneira diferente e qual estratégia utilizou.
Caso algum aluno tenha usado a calculadora para transformar todas as frações em decimais e efetuar o cálculo, o resultado não será exato, pois ? e 14/15 são dízimas periódicas e terão de ser truncadas ou arredondadas. Discuta porque esse resultado pode ser inconveniente em alguns casos. Os erros devem ser discutidos, entendidos e valorizados, pois são um importante meio para chegar no resultado certo.
Por fim, faça o questionamento do slide 14 aos alunos.
OBSERVAÇÃO: Nos slides 9 a 14, há uma interpretação visual para os dados do problema e a resolução . Se o tempo permitir, apresente as duas soluções, caso contrário, preferimos que o professor dê preferência para a solução visual, no slides 9 a 21.
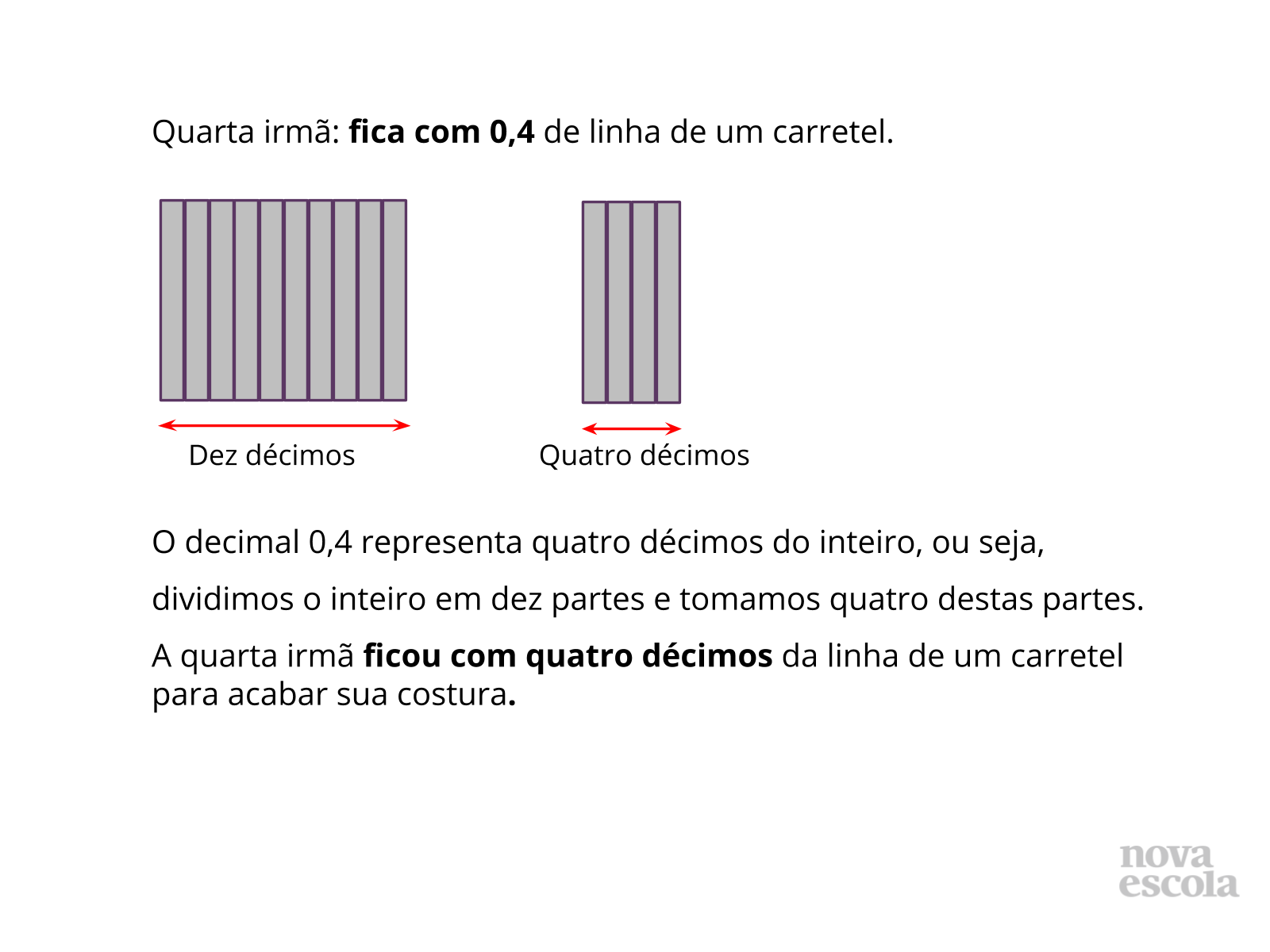
Propósito: Apresentar uma solução para a atividade principal e demonstrar a necessidade de trabalhar com partes iguais do todo ao se somar ou subtrair frações.
Discuta com a turma:
- A primeira irmã fica com 5/6 e dá quanto para Ana?;
- A segunda irmã dá para Ana 0,3 da linha de seu carretel e fica com quanto?
- A terceira irmã dá a Ana 14/15 da linha de seu carretel e fica com quanto?
Discussão das Soluções
Tempo sugerido: 15 minutos. (Slides 8 a 14)
Orientação: Inicie fazendo os questionamentos do item “Discuta com a Turma”. Só depois apresente o slide e verifique se algum aluno gostaria de expor seu cálculo no quadro. Caso ninguém consiga escrever seus pensamentos, mostre o slide ou faça essa resolução no quadro, com o auxílio deles, tanto utilizando frações quanto utilizando as representações gráficas. Sempre pergunte se alguém resolveu de maneira diferente e qual estratégia utilizou.
Caso algum aluno tenha usado a calculadora para transformar todas as frações em decimais e efetuar o cálculo, o resultado não será exato, pois ? e 14/15 são dízimas periódicas e terão de ser truncadas ou arredondadas. Discuta porque esse resultado pode ser inconveniente em alguns casos. Os erros devem ser discutidos, entendidos e valorizados, pois são um importante meio para chegar no resultado certo.
Por fim, faça o questionamento do slide 14 aos alunos.
OBSERVAÇÃO: Nos slides 9 a 14, há uma interpretação visual para os dados do problema e a resolução . Se o tempo permitir, apresente as duas soluções, caso contrário, preferimos que o professor dê preferência para a solução visual, no slides 9 a 21.
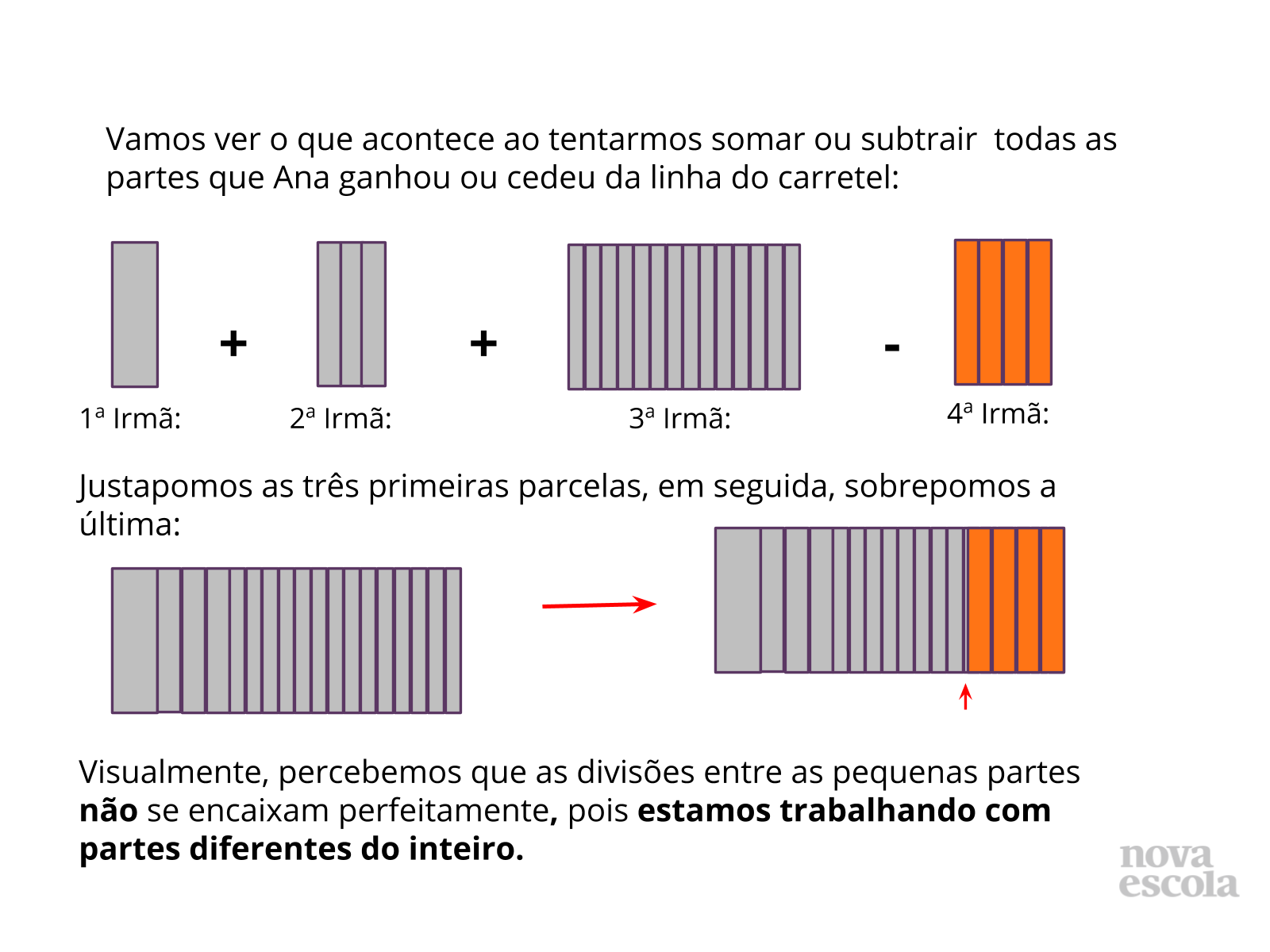
Propósito: Apresentar uma solução para a atividade principal e demonstrar a necessidade de trabalhar com partes iguais do todo ao se somar ou subtrair frações.
Discuta com a turma:
- A primeira irmã fica com 5/6 e dá quanto para Ana?;
- A segunda irmã dá para Ana 0,3 da linha de seu carretel e fica com quanto?
- A terceira irmã dá a Ana 14/15 da linha de seu carretel e fica com quanto?
Discussão das Soluções
Tempo sugerido: 15 minutos. (Slides 8 a 14)
Orientação: Inicie fazendo os questionamentos do item “Discuta com a Turma”. Só depois apresente o slide e verifique se algum aluno gostaria de expor seu cálculo no quadro. Caso ninguém consiga escrever seus pensamentos, mostre o slide ou faça essa resolução no quadro, com o auxílio deles, tanto utilizando frações quanto utilizando as representações gráficas. Sempre pergunte se alguém resolveu de maneira diferente e qual estratégia utilizou.
Caso algum aluno tenha usado a calculadora para transformar todas as frações em decimais e efetuar o cálculo, o resultado não será exato, pois ? e 14/15 são dízimas periódicas e terão de ser truncadas ou arredondadas. Discuta porque esse resultado pode ser inconveniente em alguns casos. Os erros devem ser discutidos, entendidos e valorizados, pois são um importante meio para chegar no resultado certo.
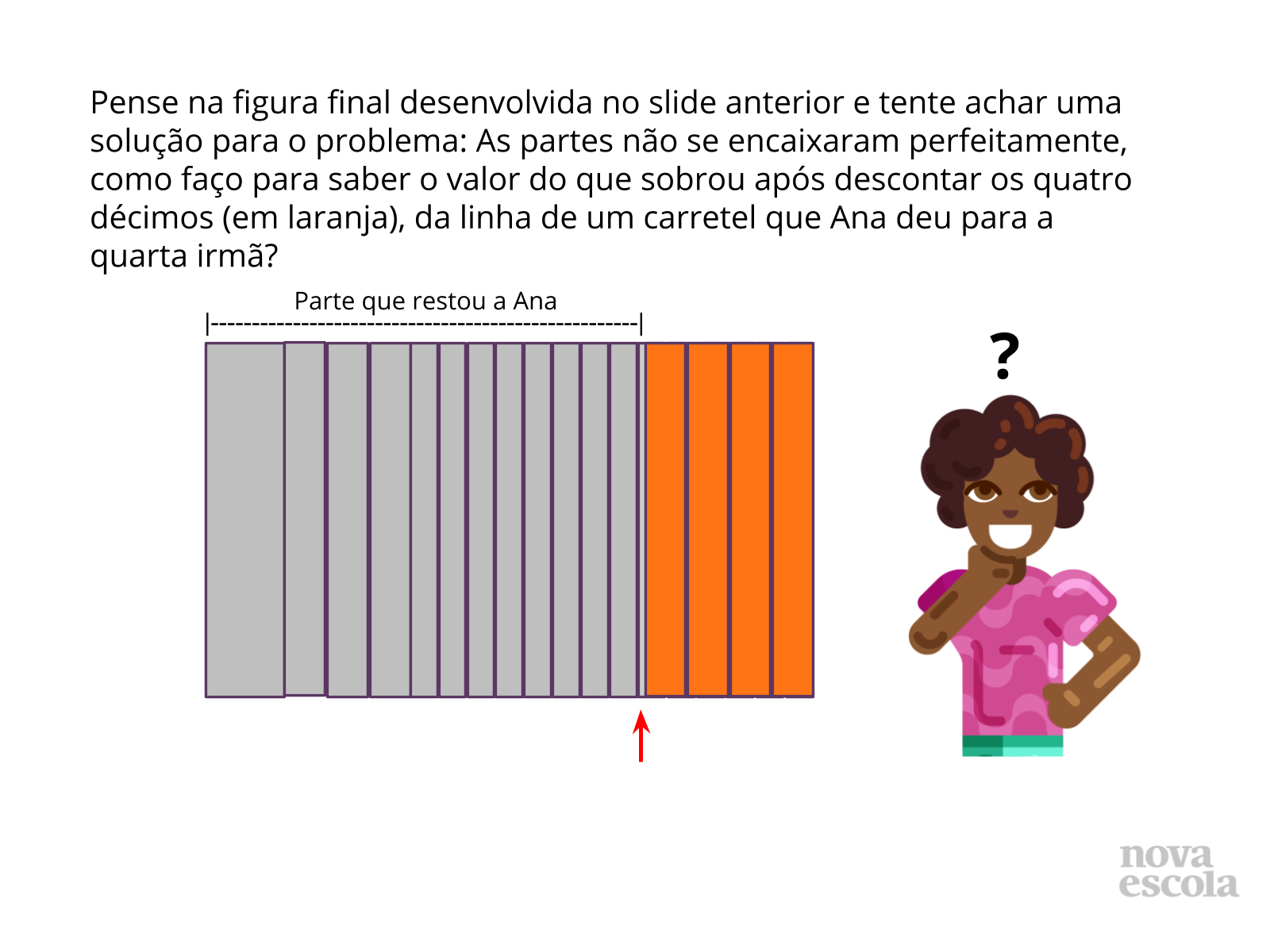
Por fim, faça o questionamento do slide 14 aos alunos.
OBSERVAÇÃO: Nos slides 9 a 14, há uma interpretação visual para os dados do problema e a resolução . Se o tempo permitir, apresente as duas soluções, caso contrário, preferimos que o professor dê preferência para a solução visual, no slides 9 a 21.
Propósito: Apresentar uma solução para a atividade principal e demonstrar a necessidade de trabalhar com partes iguais do todo ao se somar ou subtrair frações.
Discuta com a turma:
- A primeira irmã fica com 5/6 e dá quanto para Ana?;
- A segunda irmã dá para Ana 0,3 da linha de seu carretel e fica com quanto?
- A terceira irmã dá a Ana 14/15 da linha de seu carretel e fica com quanto?
Encerramento

Tempo sugerido: 5 minutos.
Orientação: Finalize a aula com a exposição deste slide, antecedendo a atividade de Raio X. Verifique se ainda há dúvidas entre os alunos antes de aplicar o Raio X.
Propósito: Revisar o assunto desenvolvido na aula e esclarecer as dúvidas da turma antes do momento de avaliação.
Discuta com a turma:
- Para somar ou subtrair frações de denominadores diferentes devemos transformar as frações em frações equivalentes de denominadores iguais, por quê?
Raio X

Tempo sugerido: 7 minutos.
Orientação: Leia junto com os alunos e verifique se todos compreenderam o problema e sabem o que devem fazer. Circule pela sala para verificar as resoluções. Lembre-se que neste momento você está avaliando os avanços dos estudantes em relação ao conteúdo da aula. Identifique as dúvidas que ainda ficaram e reserve os minutos finais da aula para uma breve correção desta atividade.
Propósito: Verificar a assimilação dos conteúdos expostos durante a aula.
Materiais Complementares:
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Altamiro Marlon Ribeiro
Mentor: Amanda Ferreira Verardo Bilia
Especialista de área: Luciana Maria Tenuta de Freitas
Objetivos Específicos
Interpretar e resolver problemas visualmente e numericamente com números racionais na forma decimal e fracionária, aplicando as operações de adição e subtração.
Conceito-chave
Fração, número decimal, operações de adição e subtração.
Recursos Necessários
- Projetor (caso haja)
- Calculadoras
- Atividades impressas em folhas, coladas no caderno ou não.