Sugestão de adaptação para ensino remoto
Ferramentas sugeridas
- Essenciais: alguma rede social: Whatsapp, Facebook etc.
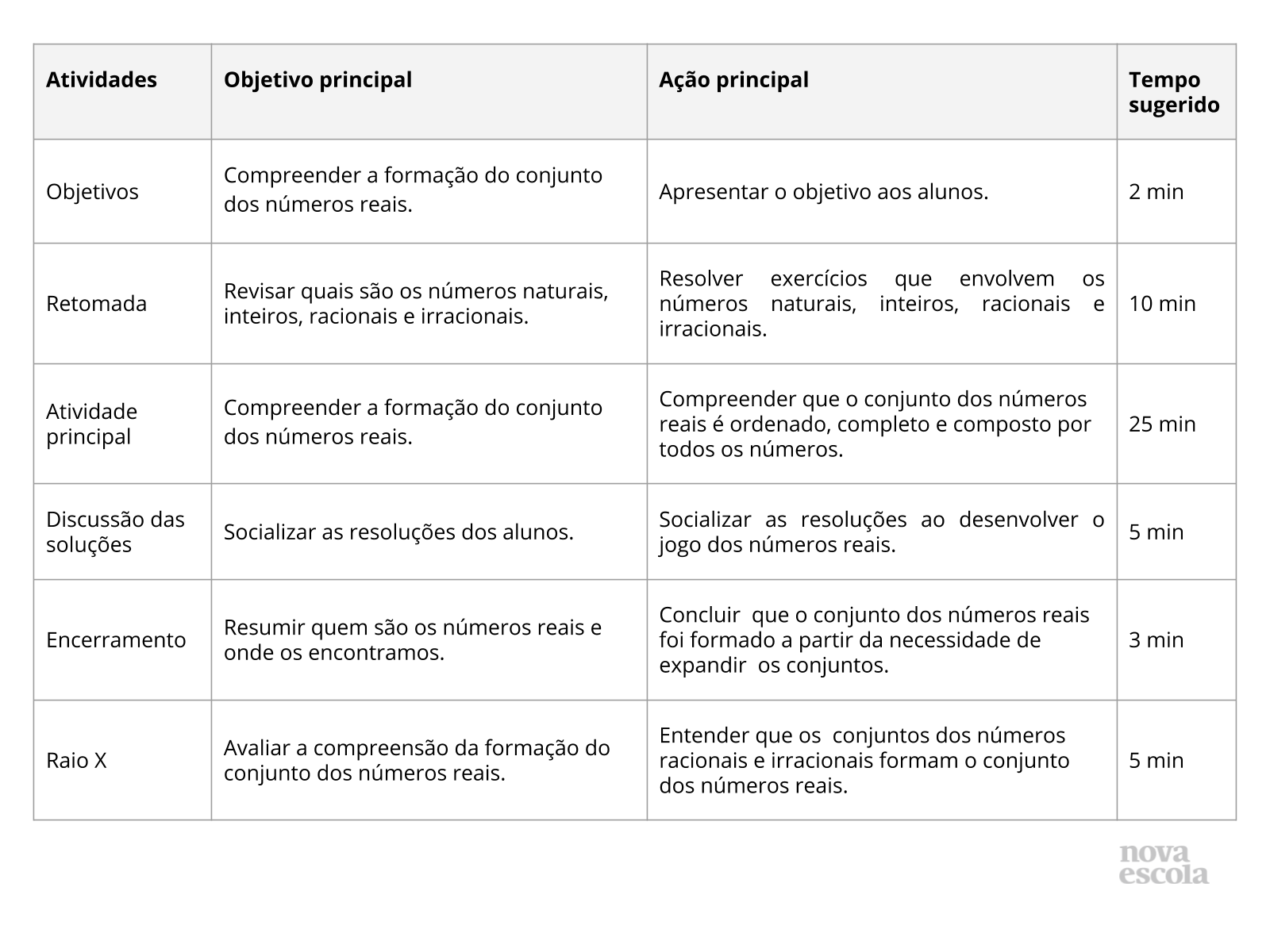
Atividade principal
Faça dessa aula um Quizz! Se possível, promova uma reunião em uma sala como a do Google Meet (disponível aqui).
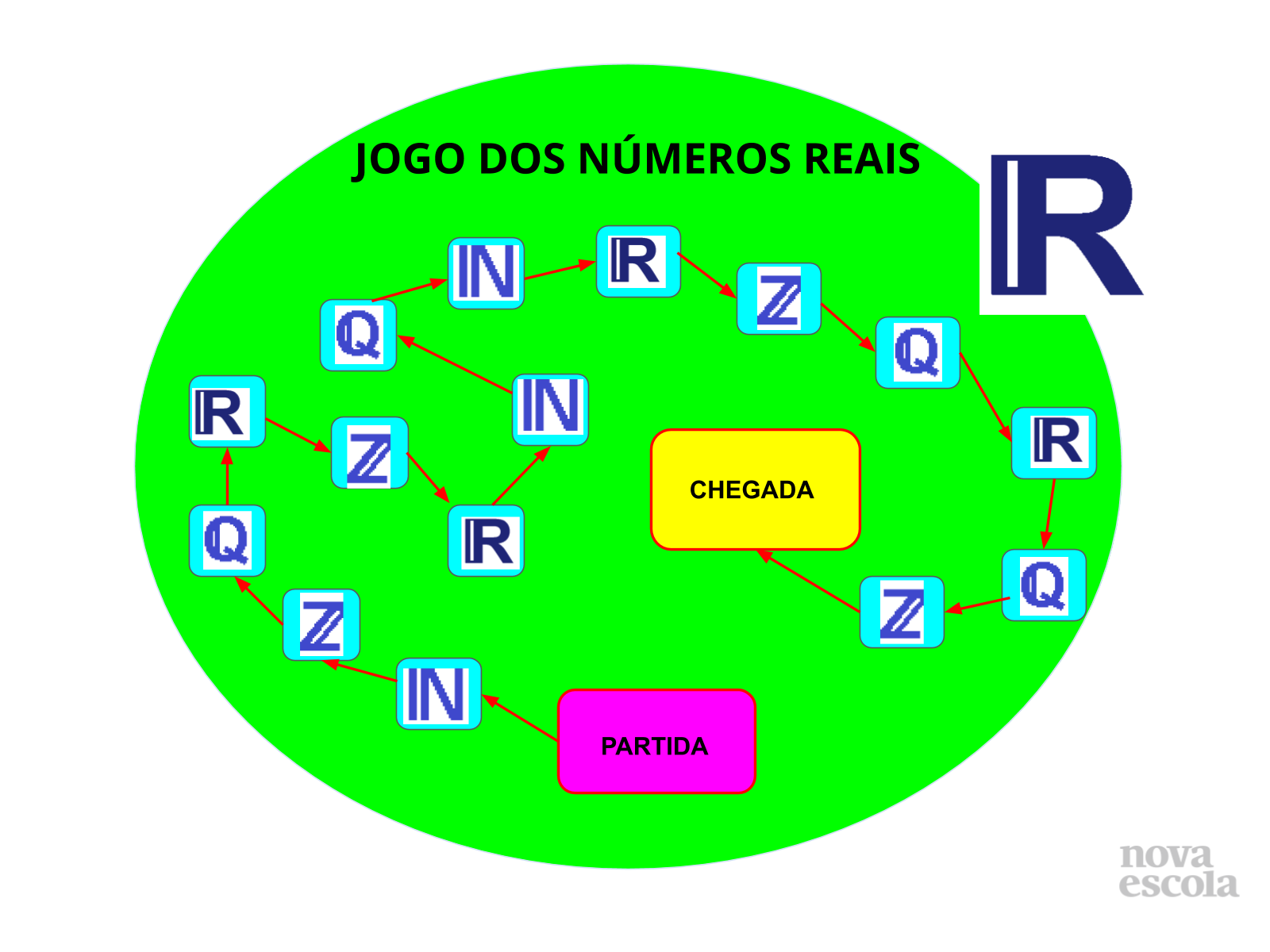
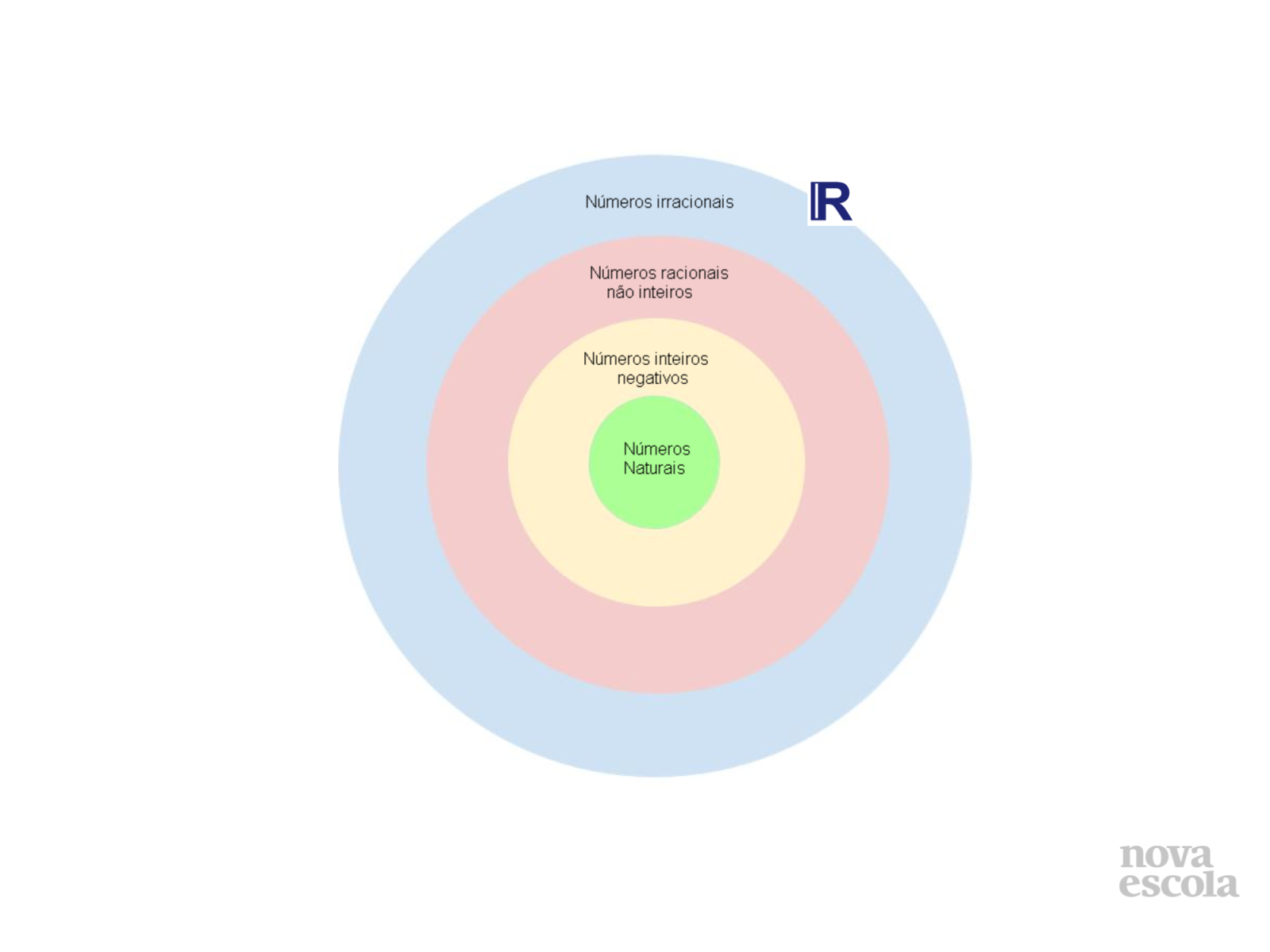
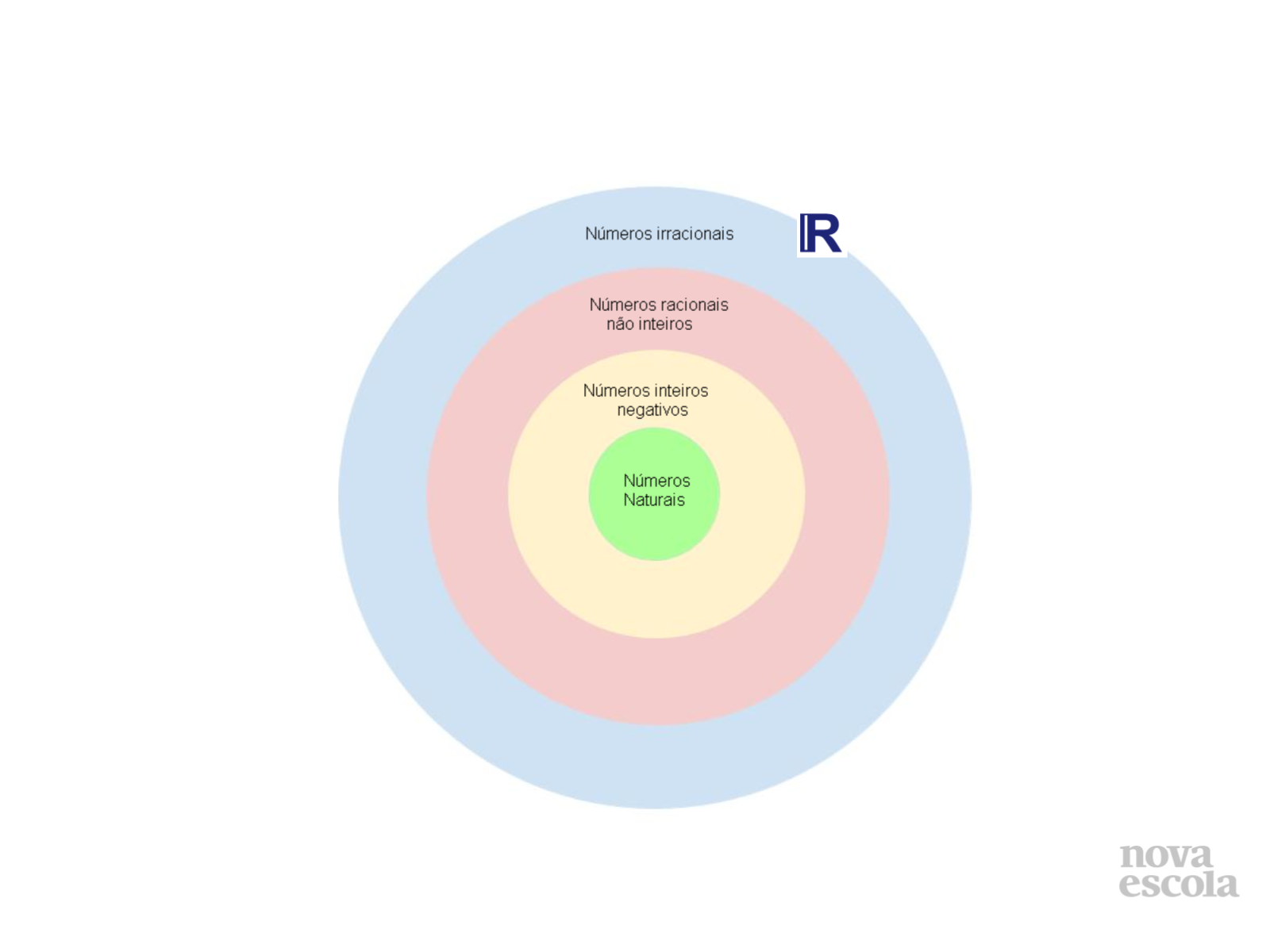
Obs.: Sugiro não considerar as representações em diagramas de Venn usadas comumente e também consideradas nos planos originais. Elas podem gerar confusões conceituais.
Pergunte:
1) No conjunto dos números naturais é possível subtrair 10 de 5? (Ou seja, tem resposta para 5 – 10?).
2) No conjunto dos inteiros, é possível realizar essa conta? Qual seria a resposta?
3) No conjunto dos naturais é possível dividir 3 por 2? (Ou seja, tem resposta para 3 : 2?).
4) ) No conjunto dos inteiros é possível dividir 3 por 2? (Ou seja, tem resposta para 3 : 2?).
5) Em qual conjunto é possível ter resposta para 3 : 2?
6) No conjunto do inteiros é possível multiplicar -2 por 0,5? Se for possível, qual é a resposta?
7) O resultado de 1,5 x 2 está em que conjuntos?
8) O número 0,44444... é racional ou irracional?
9) O número 0,43528... é racional ou irracional?
10) Desafio: Ao juntarmos um pedaço de reta medindo 2cm com outro medindo 2cm o resultado do comprimento estaria em qual conjunto numérico?
Painel de soluções
1) No conjunto dos números naturais é possível subtrair 10 de 5? (Ou seja, tem resposta para 5 – 10?) NÃO.
2) No conjunto dos inteiros, é possível realizar essa conta? SIM. Qual seria a resposta? -5.
3) No conjunto dos naturais é possível dividir 3 por 2? (Ou seja, tem resposta para 3 : 2?) NÃO.
4) No conjunto dos inteiros é possível dividir 3 por 2? (Ou seja, tem resposta para 3 : 2?) NÃO.
5) Em qual conjunto é possível ter resposta para 3 : 2? RACIONAIS. Pode ser a fração 3/2 ou o número 1,5 que é um número que tem representação decimal finita.
6) No conjunto do inteiros é possível multiplicar -2 por 0,5? Se for possível, qual é a resposta? NÃO.
7) O resultado de 1,5 x 2 está em que conjuntos? Racionais, Inteiros e Naturais, visto que satisfaz condições para se situar nos três.
8) O número 0,44444... é racional ou irracional? RACIONAL. Pois tem representação decimal finita e periódica.
9) O número 0,43528... é racional ou irracional? IRRACIONAL. Pois tem representação decimal finita e NÃO-periódica.
10) Desafio: ao juntarmos um pedaço de reta medindo 2cm com outro medindo 2 cm o resultado do comprimento estaria em qual conjunto numérico? IRRACIONAL.
Sistematização
Conclua explicando que a separação dos conjuntos numéricos está ligada às expansões de possibilidades de resultados aritméticos.
Dessa forma, reforce que dos naturais para os inteiros há um ganho em relação à subtração, com possiblidades de resultados negativos. Relembre que na multiplicação há a reflexão na reta quando usamos números negativos.
Dos inteiros para os racionais, há o ganho também na divisão, pois resultados não inteiros são possíveis, gerando decimais finitos ou dízimas periódicas.
Destaque que os naturais e inteiros também são racionais, porque as divisões entre inteiros também podem resultar nesses tipos de números (ex.: 6/2 ou 4/(-2)).
Ressalte que, entre os racionais e irracionais não há um ganho aritmético ou algébrico e sim topológico. São números que, por serem localizados por aproximações, não há uma relação de expansão e sim de completamento dos espaços da reta que ficam entre os racionais.
Encerramento
Encerre dizendo que o conjunto dos números reais é completo porque reúne os racionais e irracionais.
Raio X
Pergunte:
- É possível um número ser racional e irracional ao mesmo tempo? (NÃO).
- Será que uma soma entre dois números racionais pode ser irracional? (NÃO).
- Será que uma soma entre dois números irracionais pode ser racional? (NÃO).
Convite às famílias
Peça para os alunos pesquisarem junto aos familiares se existem mais números racionais ou irracionais como 2 ou 3, por exemplo, além de números racionais em forma de fração, para que eles identifiquem qual a posição deles.