Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
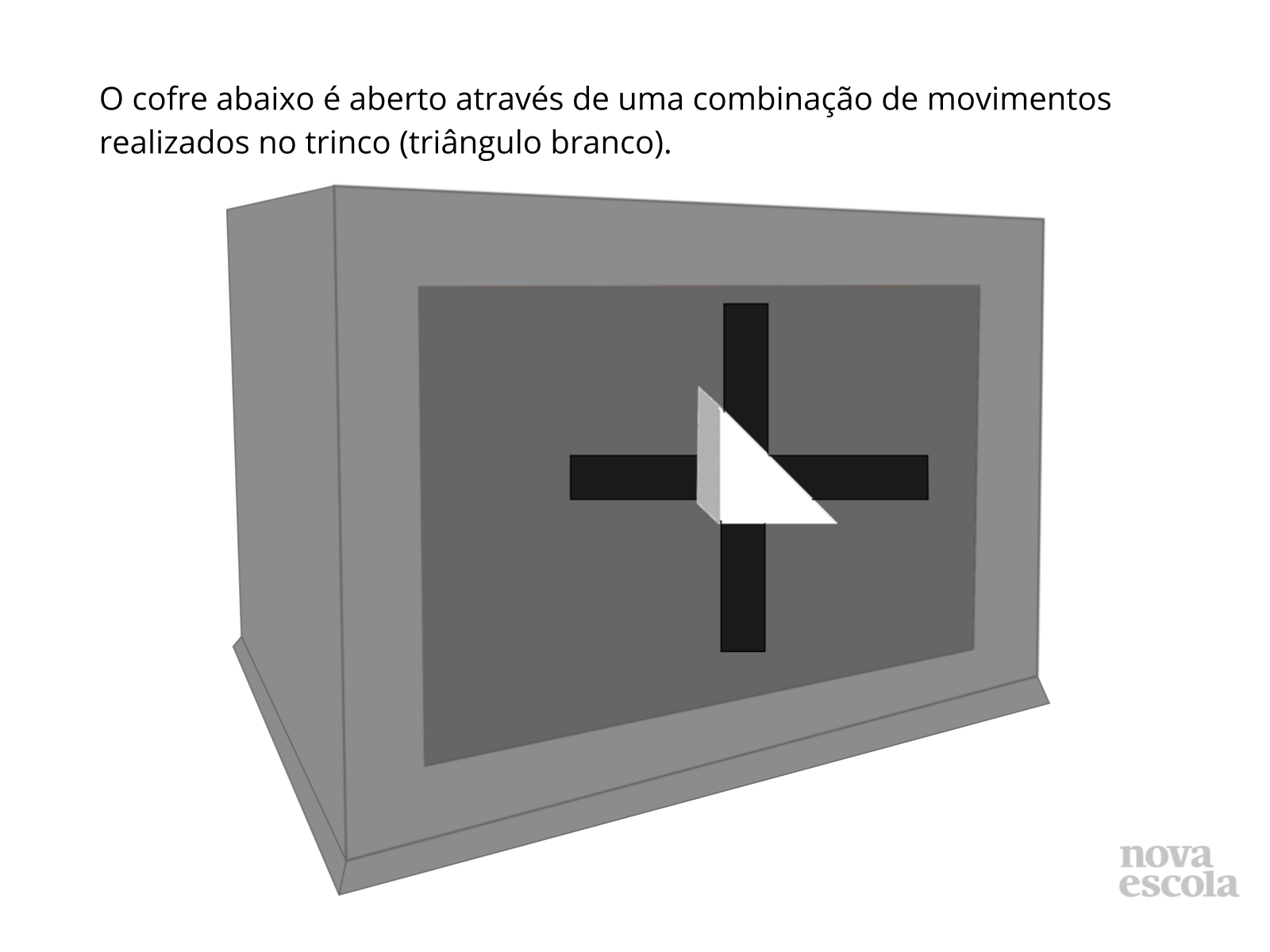
Tempo sugerido: 7 minutos (slides 3 e 4).
Orientações: Deixe que os alunos leiam a atividade e resolvam no caderno.
Propósito: Retomar quais são as transformações geométricas e reconhecê-las.
Materiais complementares para impressão:
Retomada
Resolução da Retomada
Retomada
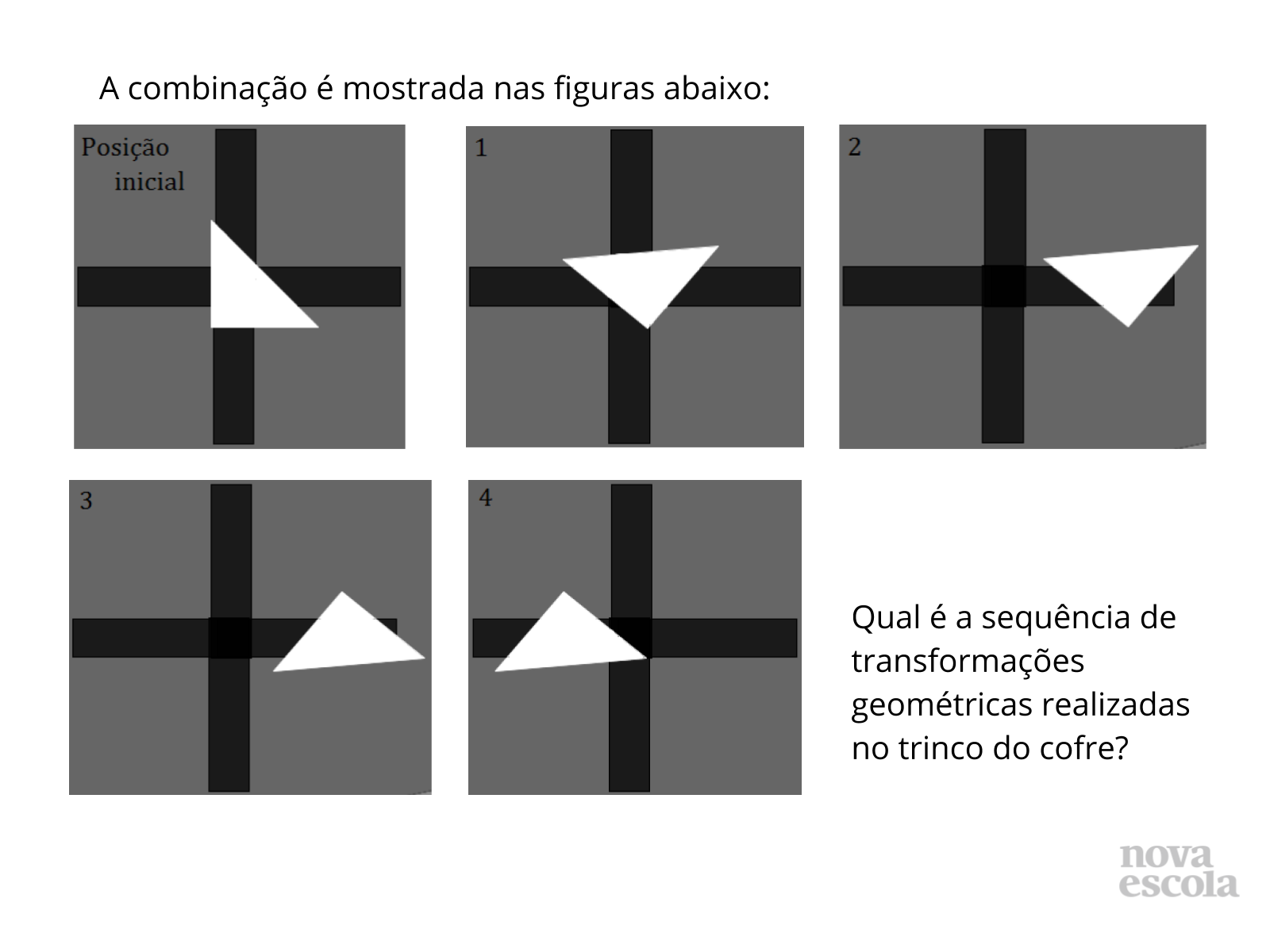
Tempo sugerido: 7 minutos (slides 3 e 4).
Orientações: Deixe que os alunos leiam a atividade e resolvam no caderno.
Propósito: Retomar quais são as transformações geométricas e reconhecê-las.
Discuta com a turma:
- Quais são as outras transformações geométricas existentes que não apareceram na combinação?
- Porque as transformações redução e ampliação não podem fazer parte de uma combinação dessa cofre?
Atividade Principal

Tempo sugerido: 16 minutos (slides 5, 6, 7, 8 e 9).
Orientações: Peça que, individualmente, os alunos leiam a atividade, respondam os itens e realizem as medições necessárias para o preenchimento da tabela utilizando régua. Oriente os alunos no preenchimento da mesma. Exemplifique realizando com eles as primeiras medições e cálculos. Circule na sala e fique atento aos comentários dos alunos, pois podem surgir dúvidas quanto a qual triângulo deve ser observado em cada iteração. Deixe que discutam com um colega e façam observações. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
Propósito: Perceber a semelhança entre todos os triângulos e chegar nas relações entre os perímetros e áreas de triângulos semelhantes.
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal
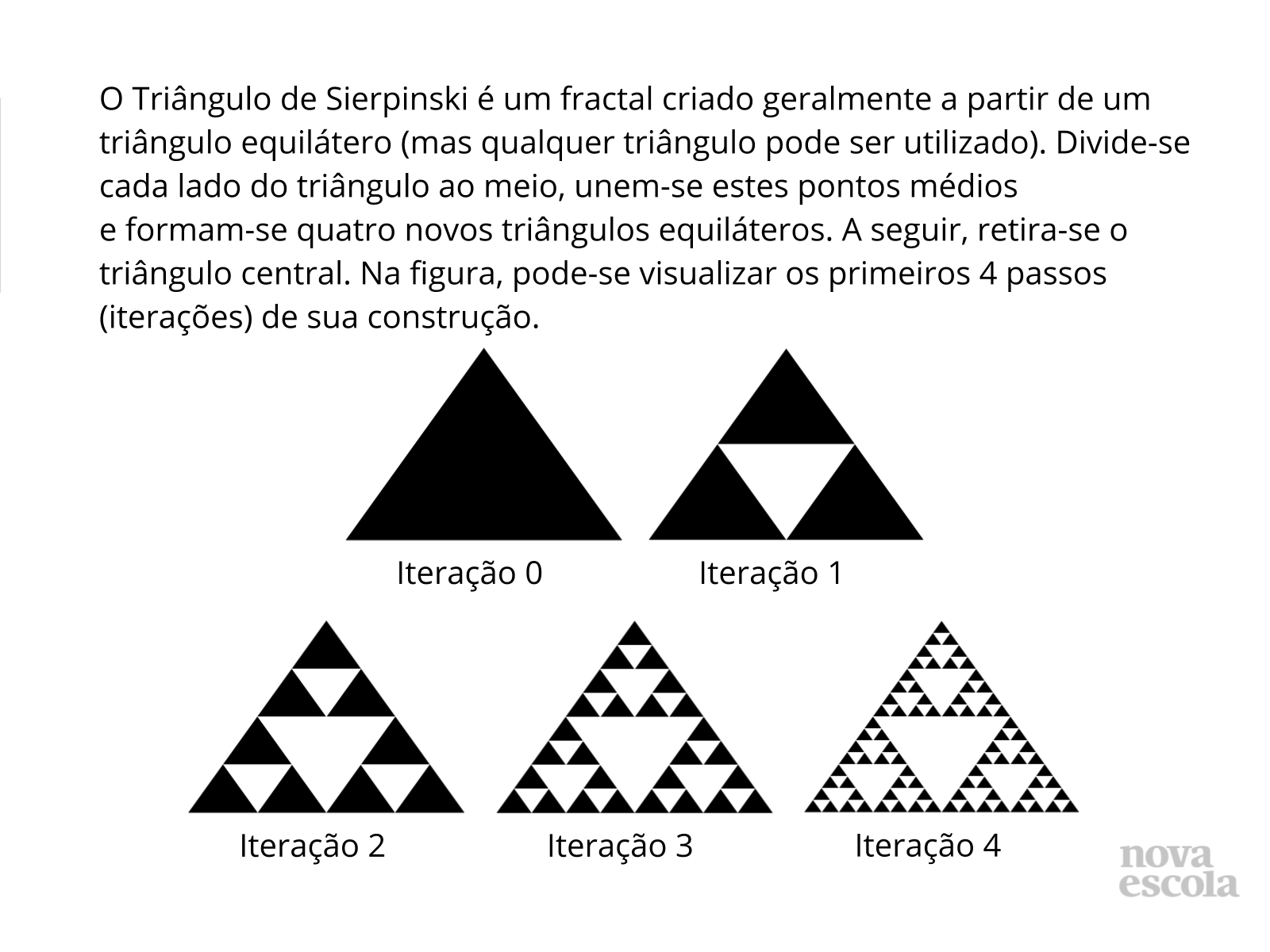
Tempo sugerido: 16 minutos (slides 5, 6, 7, 8 e 9).
Orientações: Certifique que os alunos compreenderam bem o processo de construção do Triângulo de Sierpinski.
Propósito: Facilitar a percepção de que os triângulos são semelhantes.
Atividade Principal

Tempo sugerido: 16 minutos (slides 5, 6, 7, 8 e 9).
Orientações: Questione os alunos quanto às diferenças entre este e o triângulo do slide anterior. Anote as respostas dos alunos dos questionamentos do discuta com a turma, ou solicite que algum aluno o faça. Dessa forma, estas respostas podem ser retomadas na discussão das soluções para verificar se as ideias dos alunos mudaram depois de realizada a atividade.
Propósito: Perceber que os triângulos são semelhantes e relacionar a semelhança com as transformações geométricas.
Discuta com a turma:
- Qual a diferença entre este triângulo e o do slide anterior?
- O processo de construção foi o mesmo?
- O que acontece com os lados dos novos triângulos de cada iteração com relação aos lados dos triângulos da iteração anterior?
Atividade Principal

Tempo sugerido: 16 minutos (slides 5, 6, 7, 8 e 9).
Orientações: Circule na sala e acompanhe o processo de preenchimento da tabela, auxiliando os alunos se for necessário. Atente-se ao fato de que as medidas apresentadas aqui são das construções do Triângulo de Sierpinski no GeoGebra, podendo divergir das medidas na impressão encontradas pelos alunos. Você pode deixar que os alunos utilizem calculadora para agilizar os cálculos, já que o objetivo principal é obter as relações entre os perímetros e áreas de triângulos semelhantes.
Propósito: Preenchimento da tabela.
Atividade Principal

Tempo sugerido: 16 minutos (slides 5, 6, 7, 8 e 9).
Orientações: Após os alunos terem lido e refletido sobre os dados da tabela, sugira que se reúnam em duplas para discutirem o que já pensaram e juntos compreenderem melhor as situações e chegarem a conclusões a respeito do perímetro e área de triângulos semelhantes.
Propósito: Obter relações entre os perímetros e áreas de triângulos semelhantes.
Discuta com a turma:
- O que está acontecendo com os valores dos perímetros?
- Ocorre o mesmo com os valores das áreas?
Discussão da Solução

Tempo sugerido: 15 minutos (slides 10, 11, 12, 13 e 14).
Orientações: Convide alguns alunos a exporem seus resultados. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos.
Propósito: Discutir com os alunos as respostas obtidas e retomar conceitos que se referem à semelhança de triângulos.
Discuta com a turma:
- Se tomássemos como referência um triângulo da iteração 4, qual seria a transformação geométrica pela qual os triângulos das iterações anteriores seriam originados?
Discussão da Solução
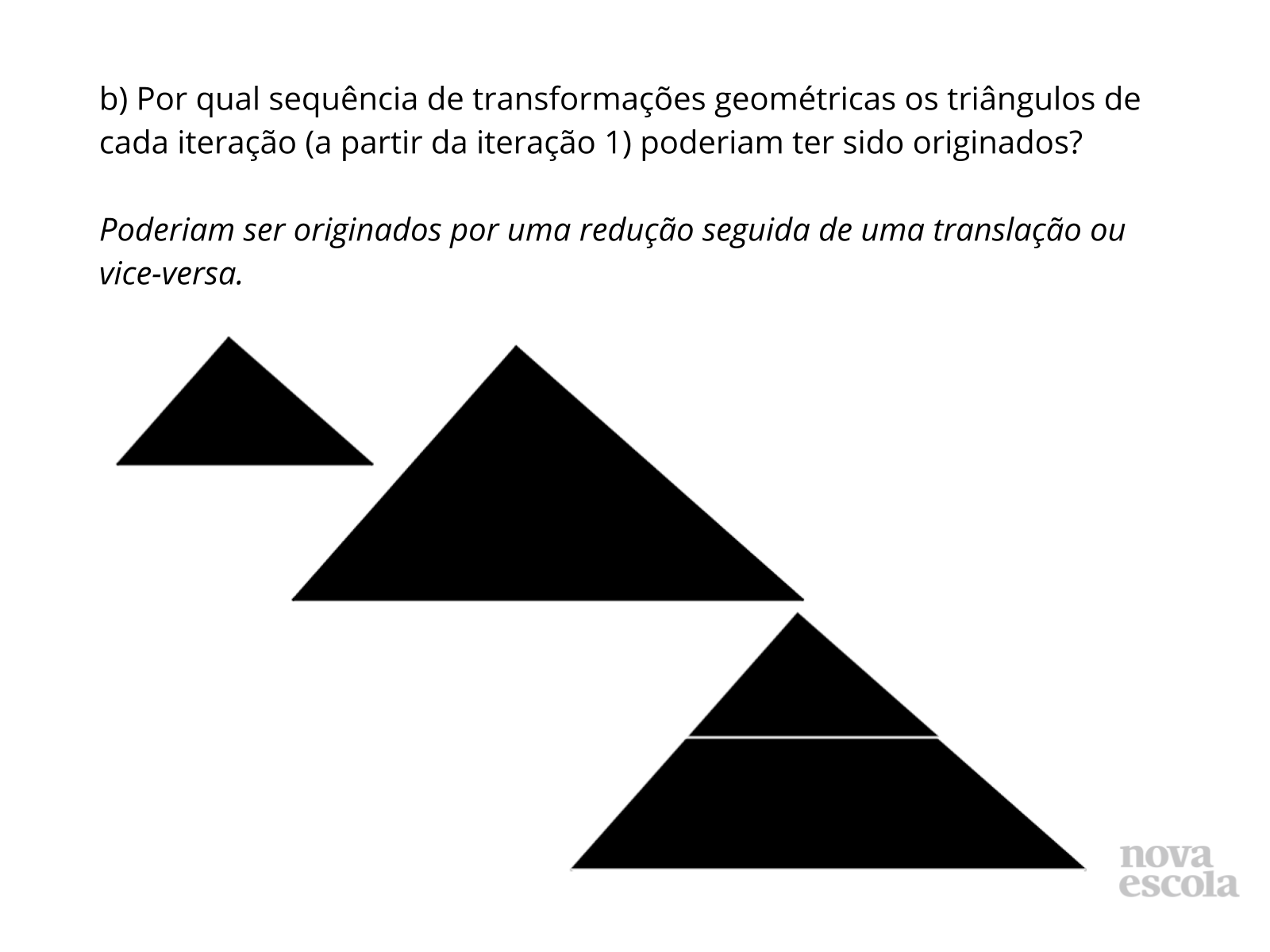
Tempo sugerido: 15 minutos (slides 10, 11, 12, 13 e 14).
Orientações: Convide alguns alunos a exporem seus resultados. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos.
Propósito: Discutir com os alunos as respostas obtidas e retomar conceitos que se referem à semelhança de triângulos.
Discussão da Solução
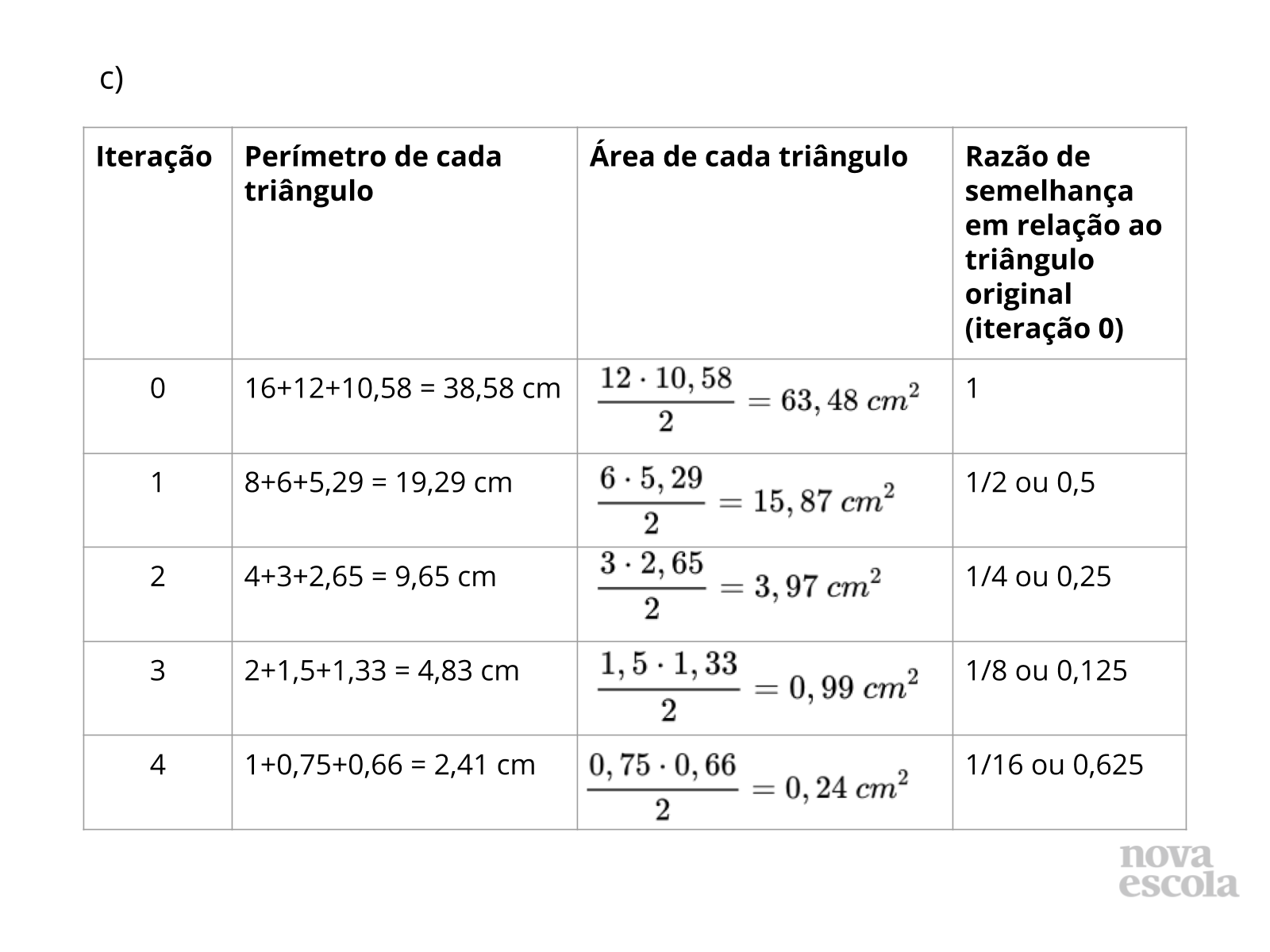
Tempo sugerido: 15 minutos (slides 10, 11, 12, 13 e 14).
Orientações: Convide alguns alunos a exporem seus resultados. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos. Atente-se ao fato de que as medidas apresentadas aqui são das construções do Triângulo de Sierpinski no GeoGebra, podendo divergir das medidas na impressão encontradas pelos alunos.
Propósito: Discutir com os alunos as respostas obtidas e retomar conceitos que se referem à semelhança de triângulos.
Discuta com a turma:
- Há uma regularidade na forma com que os perímetros diminuem no decorrer das iterações? Que regularidade é essa?
- Há uma regularidade na forma com que as áreas diminuem no decorrer das iterações? Que regularidade é essa?
Discussão da Solução

Tempo sugerido: 15 minutos (slides 10, 11, 12, 13 e 14).
Orientações: Convide alguns alunos a exporem seus resultados. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos. Explique aos alunos que na expressão P’ é o perímetro do triângulo transformado, P, o perímetro do triângulo original e r a razão de semelhança. Outra relação que pode ser encontrada pelos alunos ou abordada por você é P(1/2)^n, em que n representa a iteração. Essa é uma relação específica para reduções sucessivas à metade.
Propósito: Discutir com os alunos as respostas obtidas e retomar conceitos que se referem à semelhança de triângulos.
Discuta com a turma:
- Essa relação é válida também quando ampliamos um triângulo?
- Essa relação é válida também para retângulos semelhantes?
Discussão da Solução

Tempo sugerido: 15 minutos (slides 10, 11, 12, 13 e 14).
Orientações: Convide alguns alunos a exporem seus resultados. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos. Explique aos alunos que na expressão A’ é a área do triângulo transformado, A, a área do triângulo original e r a razão de semelhança. Outra relação que pode ser encontrada pelos alunos ou abordada por você é A(1/4)^n, em que n representa a iteração. Essa é uma relação específica para reduções sucessivas à metade.
Propósito: Discutir com os alunos as respostas obtidas e retomar conceitos que se referem à semelhança de triângulos.
Discuta com a turma:
- Essa relação é válida também quando ampliamos um triângulo?
- Essa relação é válida também para retângulos semelhantes?
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade retomando com os estudantes o Triângulo de Sierpinski e os conceitos trabalhados por meio dele. Peça que leiam a conclusão e registrem no caderno a respeito da relação entre os perímetros e a relação entre as áreas de triângulos semelhantes.
Propósito: Retomar os conceitos envolvidos na atividade principal.
Raio X
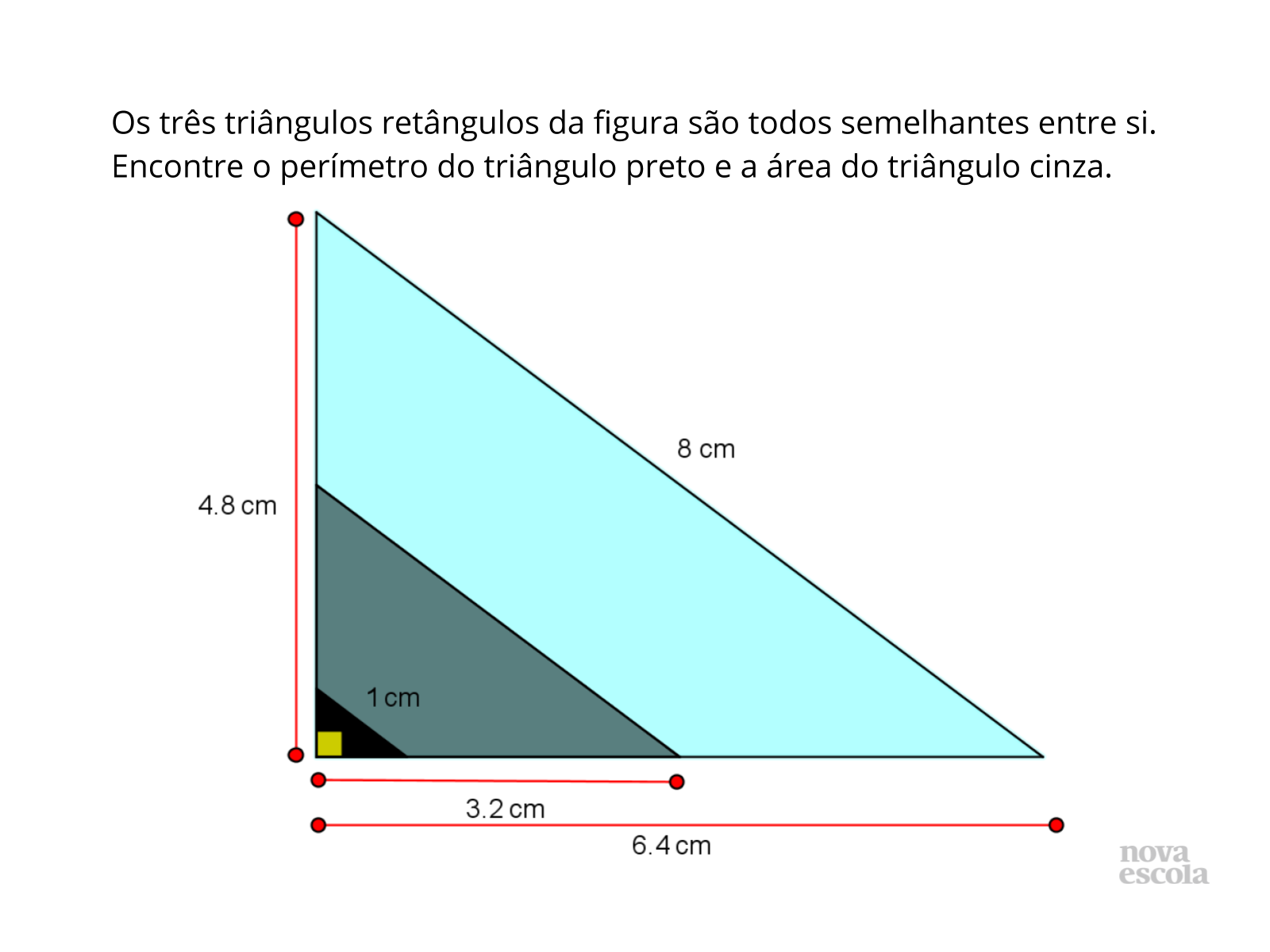
Tempo sugerido: 8 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos no que se refere à relação existente entre os perímetros e a relação entre as áreas de triângulos semelhantes.
Discuta com a turma:
- É possível calcular o perímetro do triângulo cinza? De quais formas?
- É possível calcular a área do triângulo preto? De quais formas?
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar