Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Apresentar o objetivo para que fique claro o que se deseja atingir com essa aula.
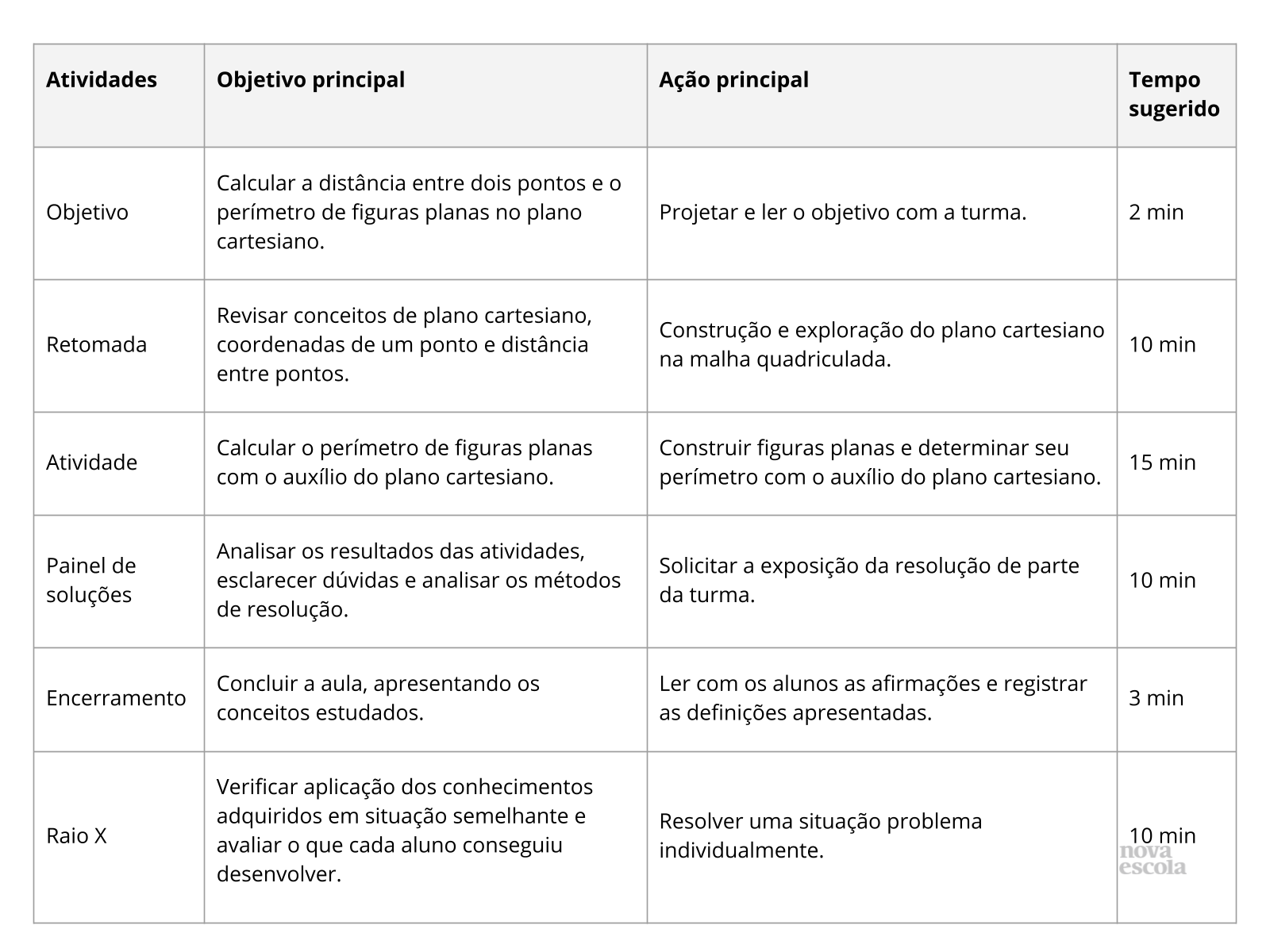
Retomada
Tempo sugerido: 10 minutos (slides 3 e 4).
Orientações: Prepare o material antes da aula e solicite com antecedência a régua aos alunos. Discuta as perguntas com os alunos antes de prosseguir para o próximo slide.
Propósito: Revisar conceitos de plano cartesiano, coordenadas de um ponto e distância entre pontos.
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Retomada

Tempo sugerido: 10 minutos (slides 3 e 4).
Orientações: Prepare o material antes da aula e solicite com antecedência a régua aos alunos. Professor, caminhe pela sala para garantir a interação durante a troca das construções. Cada aluno fará uma construção diferente. Oriente e verifique se os alunos estão calculando a distância entre os pontos escolhidos corretamente.
Propósito: Revisar conceitos de plano cartesiano, coordenadas de um ponto e segmento de reta.
Discuta com a Turma:
- Como são distribuídos os quadrantes no plano?
- Quais os quadrantes as abscissas apresentam valores negativos?
- Quais os quadrantes as ordenadas apresentam valores negativos?
- O que significa mudar a escala?
- Quando o segmento formado pela união dos pontos é horizontal, como calcular a distância entre eles?
- Quando o segmento formado pela união dos pontos é vertical, como calcular a distância entre eles?
- Quando o segmento formado pela união dos pontos é uma diagonal, como calcular a distância entre eles?
Materiais complementares:
Aquecimento
Resolução do Aquecimento
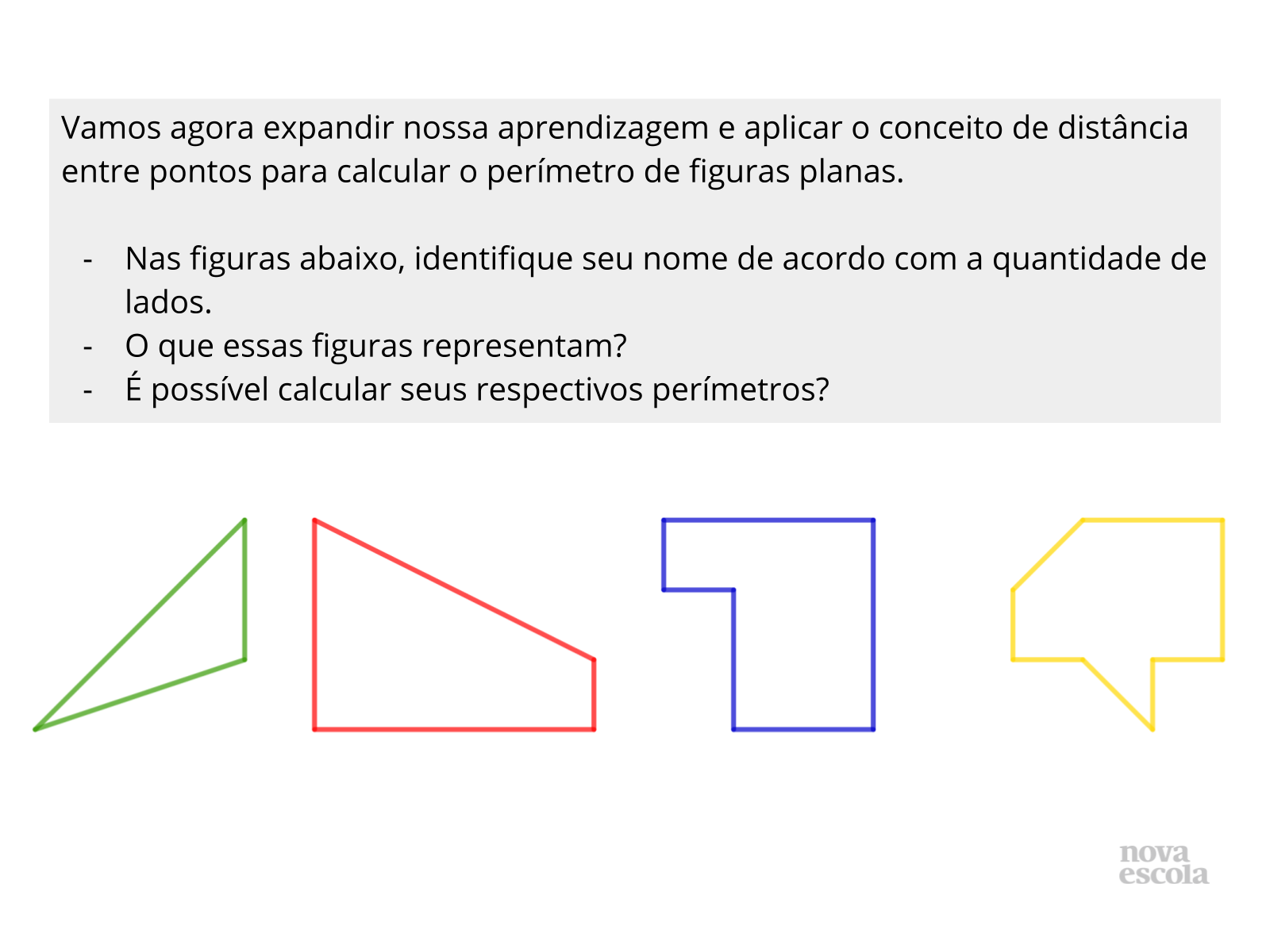
Atividade Principal
Tempo sugerido: 15 minutos (slides 5 e 6).
Orientações: Prepare o material antes da aula e solicite com antecedência a régua aos alunos. Professor, caminhe pela sala para garantir a participação de todos os alunos na realização da atividade.
Propósito: Calcular o perímetro de figuras planas com o auxílio do plano cartesiano.
Discuta com a Turma:
- O que são polígonos?
- Existem dois tipos de polígonos, quais são eles? Identifique nos polígonos propostos na atividade.
- Como calcular o perímetro de um polígono?
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal
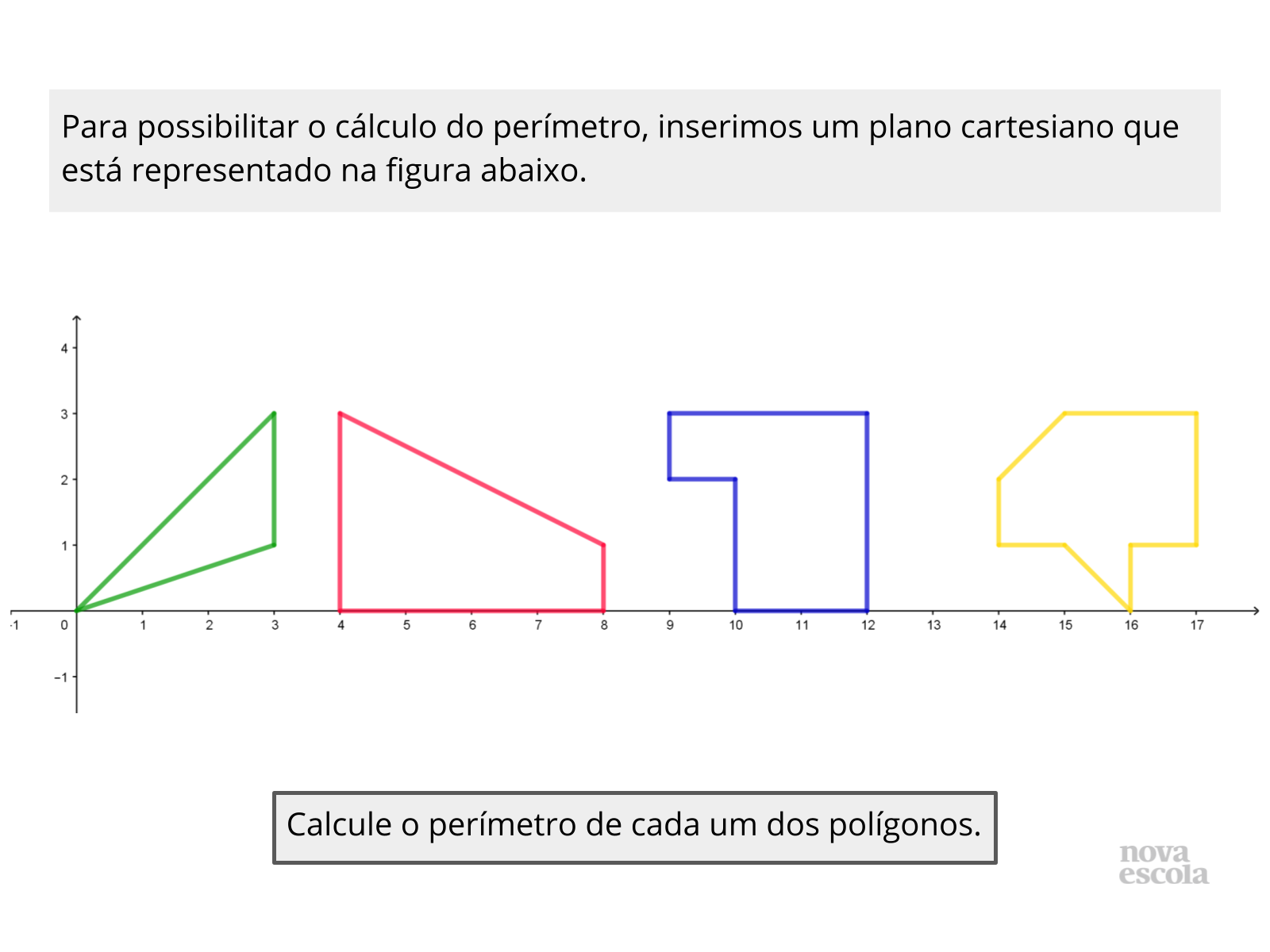
Tempo sugerido: 15 minutos (slides 5 e 6).
Orientações: Prepare o material antes da aula e solicite com antecedência a régua aos alunos. Professor, caminhe pela sala para garantir a participação de todos os alunos na realização da atividade.
Propósito: Calcular o perímetro de figuras planas com o auxílio do plano cartesiano.
Discuta com a Turma:
- Há necessidade da construção da malha quadriculada?
- Há necessidade de saber a coordenada de cada um dos pontos?
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão da solução
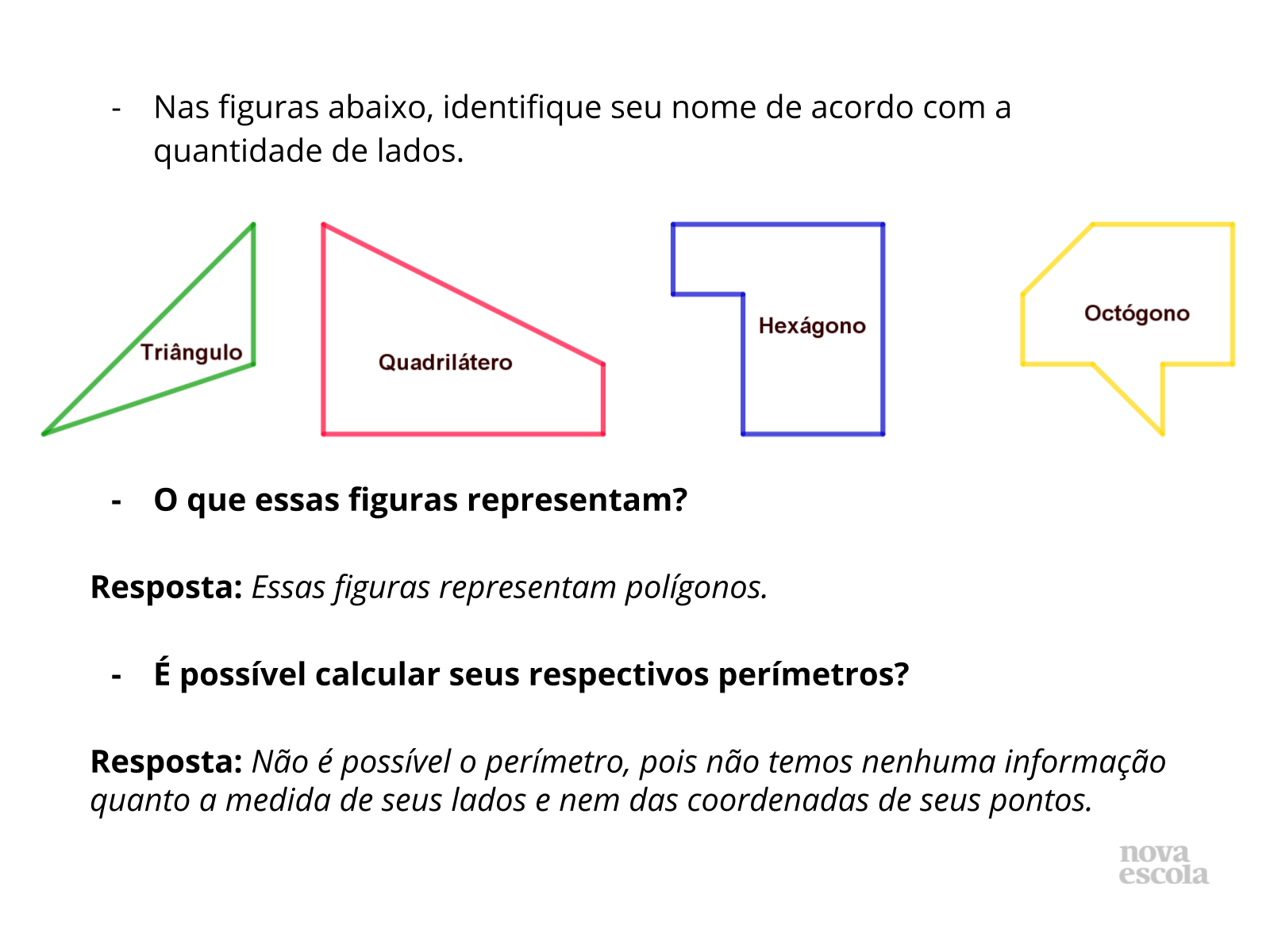
Tempo sugerido: 10 minutos (slides 7 e 8).
Orientações: Peça para que alguns alunos da turma apresentem as soluções a que chegaram. Não deixe de indagar sobre possíveis resoluções diferentes.
Propósito: Discutir com os alunos as resoluções.
Discuta com a turma:
- O que é um polígono convexo? Identifique na atividade.
- O que é um polígono não convexo? Identifique na atividade.
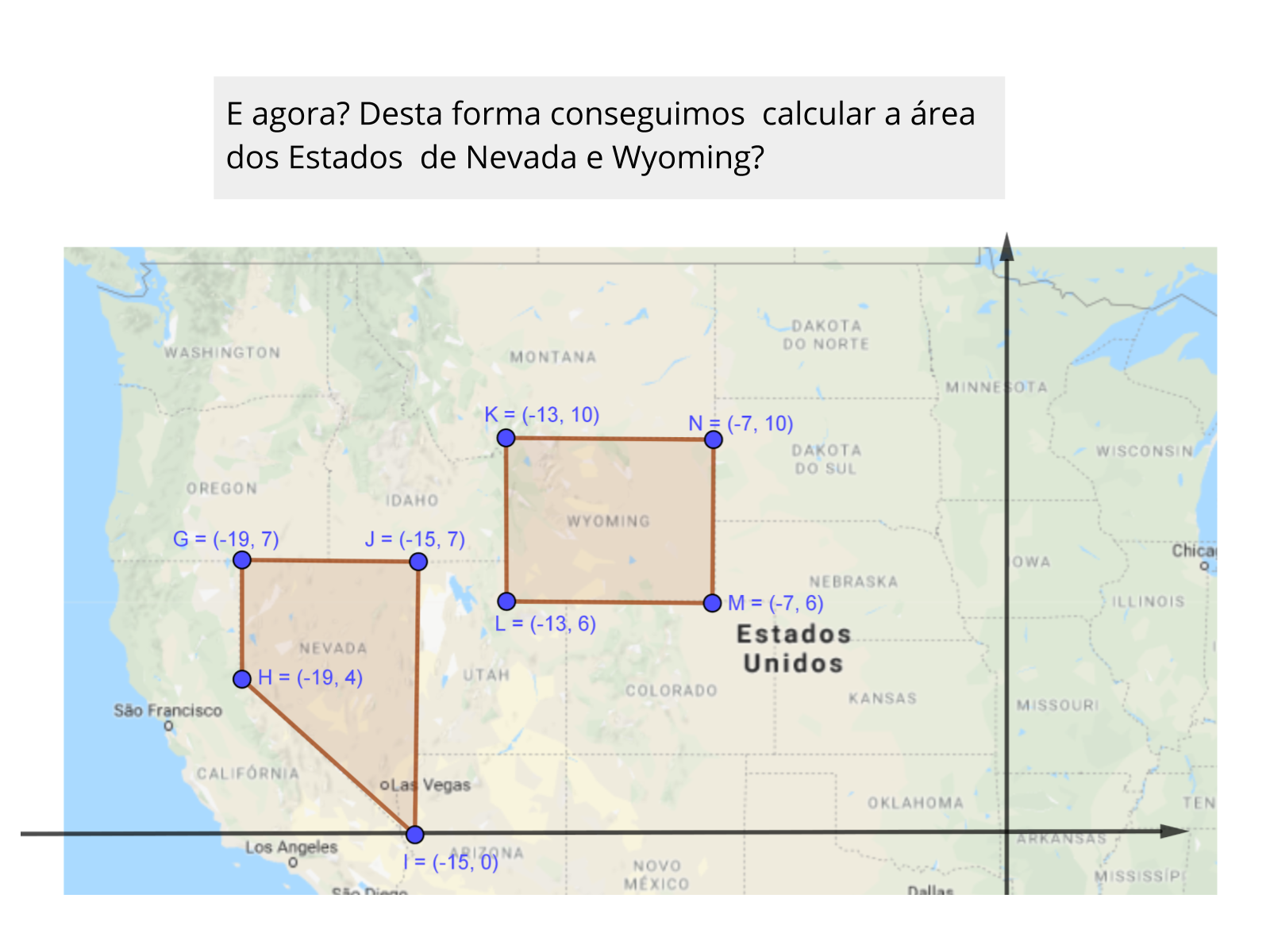
- O que podemos fazer para que seja possível calcular o perímetro dos polígonos diferente do proposto na atividade?
Discussão da solução

Tempo sugerido: 10 minutos (slides 8 a 12).
Orientações: Peça para que alguns alunos da turma apresentem as soluções a que chegaram. Não deixe de indagar sobre possíveis resoluções diferentes. Para responder a pergunta em destaque, relembre com os alunos o transporte de segmentos utilizando o compasso.
Propósito: Discutir com os alunos as resoluções.
Discuta com a turma:
- Como saber entre quais números inteiros os números irracionais estão?
Discussão da solução
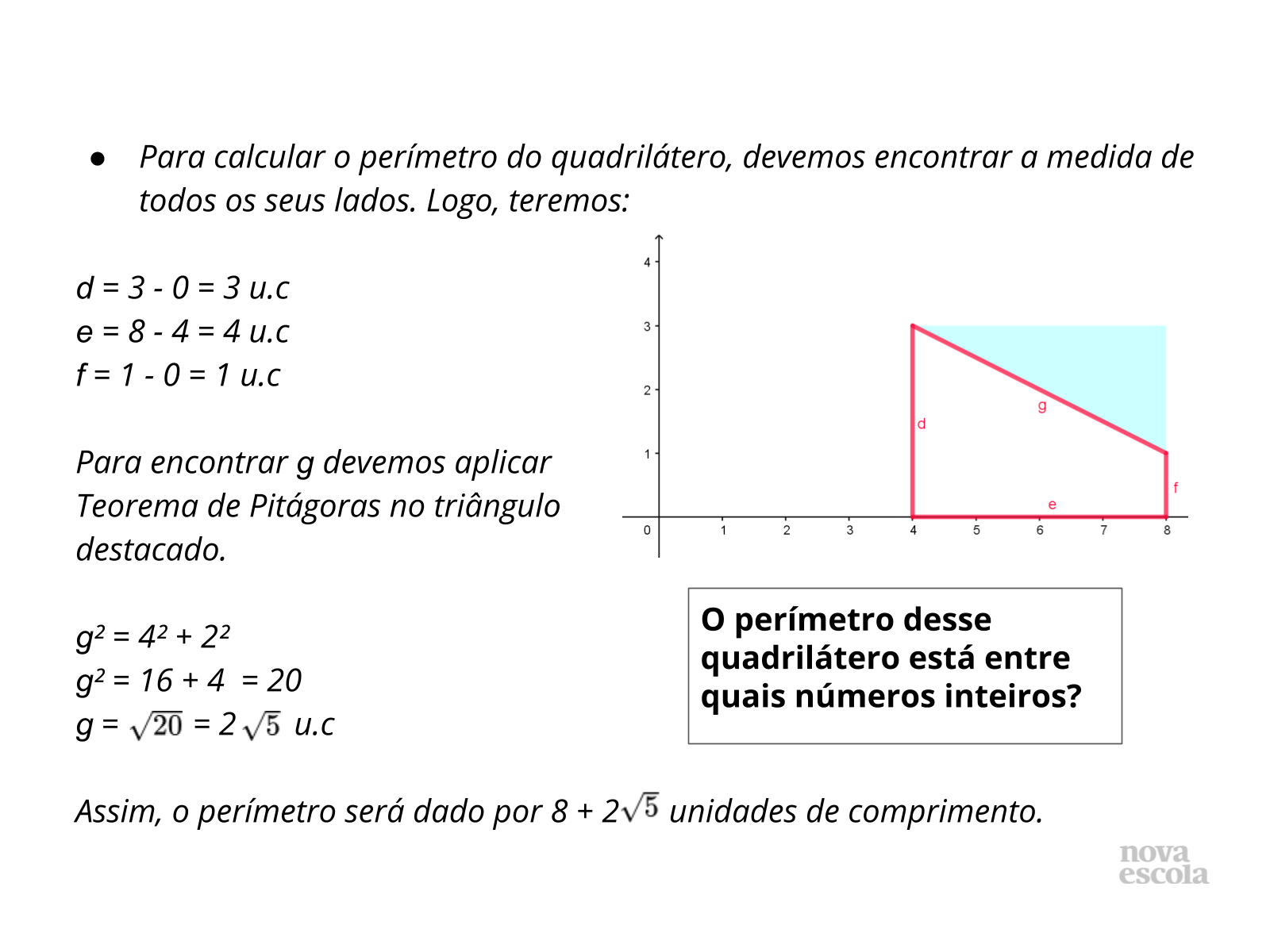
Tempo sugerido: 10 minutos (slides 8 a 12).
Orientações: Peça para que alguns alunos da turma apresentem as soluções a que chegaram. Não deixe de indagar sobre possíveis resoluções diferentes. Para responder a pergunta em destaque, relembre com os alunos o transporte de segmentos utilizando o compasso.
Propósito: Discutir com os alunos as resoluções.
Discuta com a turma:
- Podemos escolher outro triângulo retângulo para aplicar o Teorema de Pitágoras e encontrar o comprimento do segmento g?
Discussão da solução
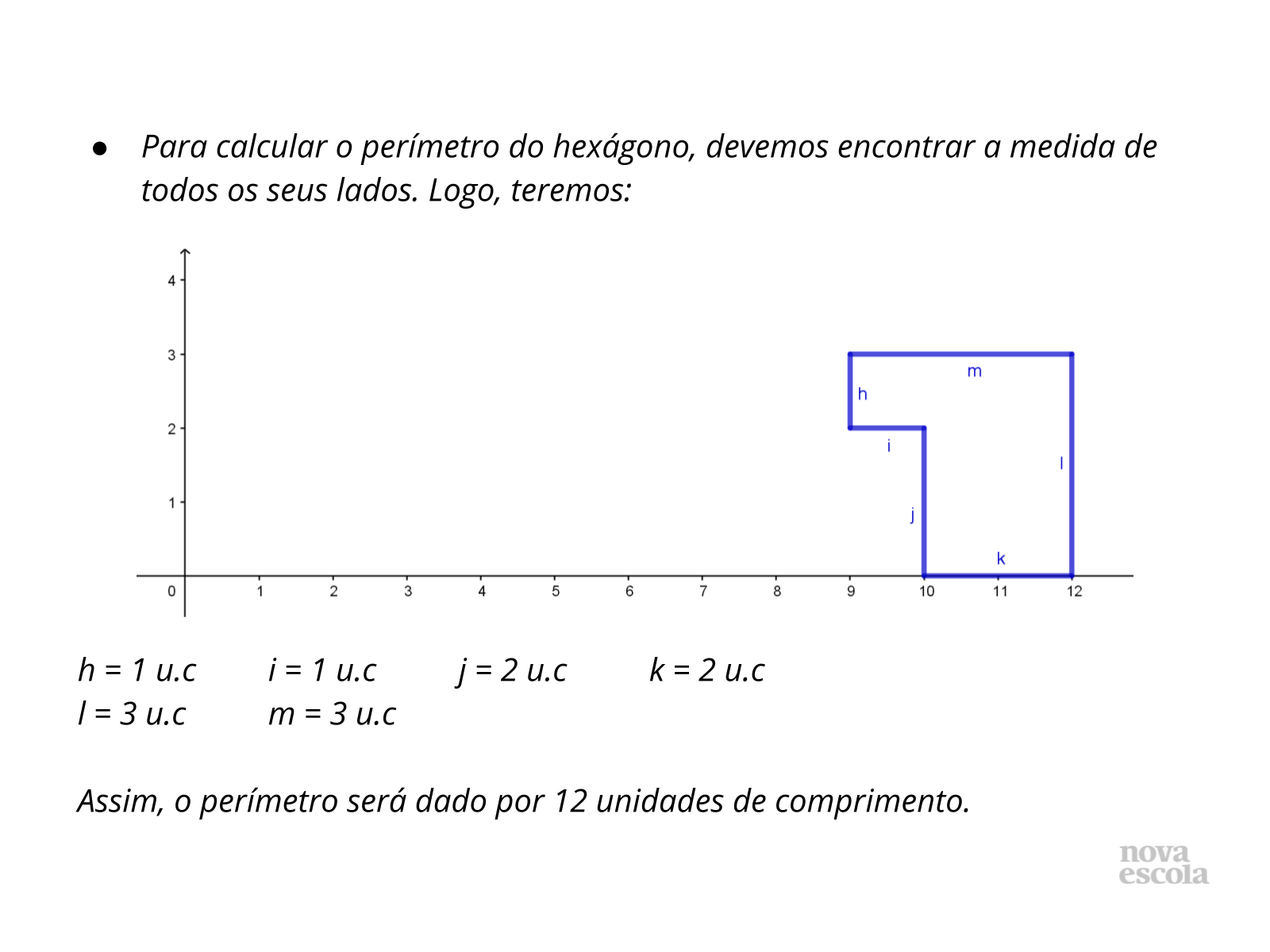
Tempo sugerido: 10 minutos (slides 8 a 12).
Orientações: Peça para que alguns alunos da turma apresentem as soluções a que chegaram. Não deixe de indagar sobre possíveis resoluções diferentes. Para responder a pergunta em destaque, relembre com os alunos o transporte de segmentos utilizando o compasso.
Propósito: Discutir com os alunos as resoluções.
Discuta com a turma:
- Quando os segmentos estão na vertical, como é calculado seu comprimento? Esse segmento é paralelo a qual eixo coordenado?
- Quando os segmentos estão na horizontal, como é calculado seu comprimento? Esse segmento é paralelo a qual eixo coordenado?
Discussão da solução

Tempo sugerido: 10 minutos (slides 8 a 12).
Orientações: Peça para que alguns alunos da turma apresentem as soluções a que chegaram. Não deixe de indagar sobre possíveis resoluções diferentes. Para responder a pergunta em destaque, relembre com os alunos o transporte de segmentos utilizando o compasso.
Propósito: Discutir com os alunos as resoluções.
Discuta com a turma:
- O que garante que os dois triângulos em destaque são semelhantes e congruentes?
Discussão da solução
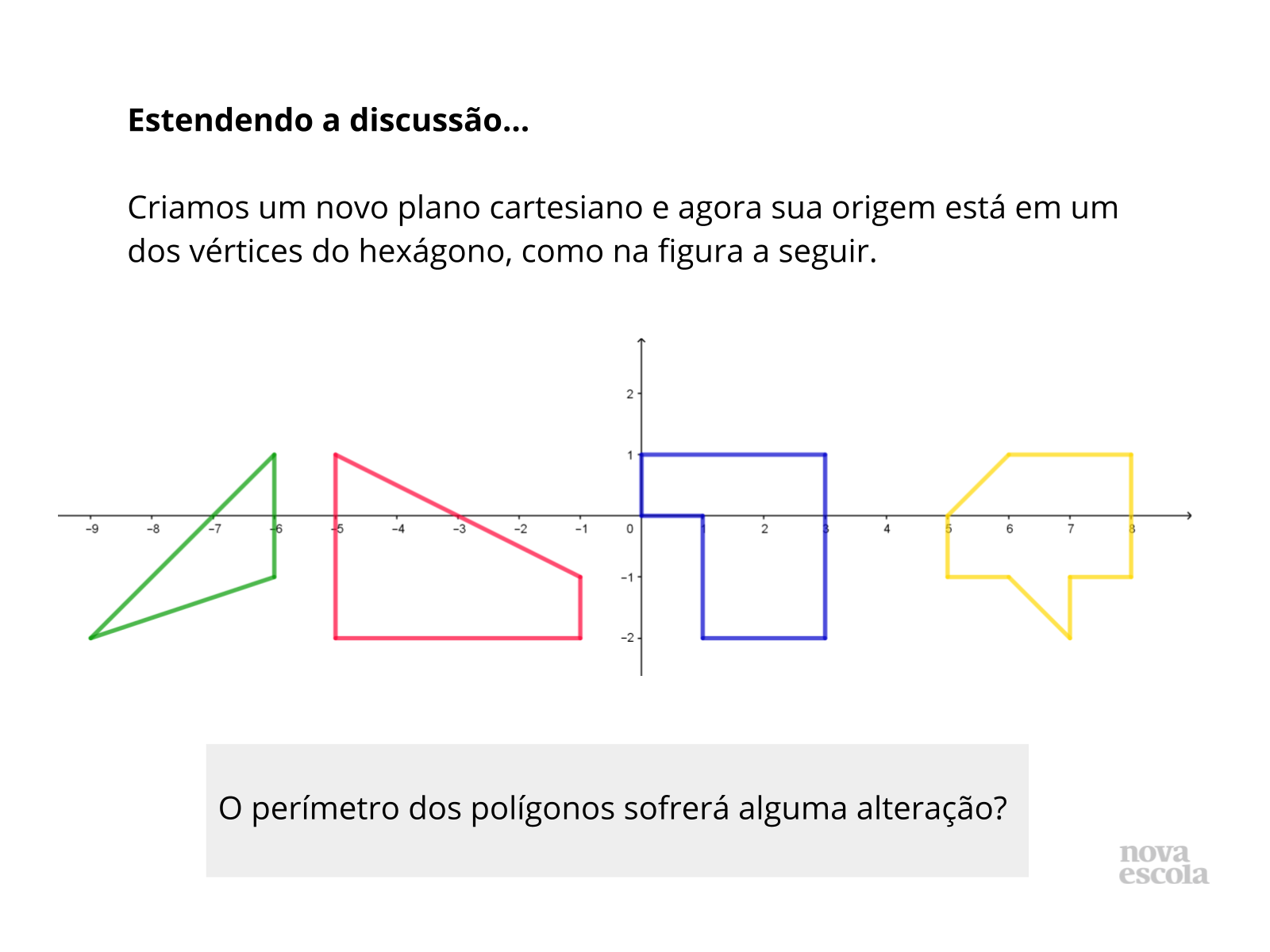
Tempo sugerido: 10 minutos (slides 8 a 12).
Orientações: Faça o questionamento aos alunos e apresente algumas situações mostrando que, independente da localização no plano cartesiano, a distância entre os pontos se mantém.
Propósito: Discutir com os alunos possíveis mudanças na construção do plano cartesiano.
Encerramento

Tempo sugerido: 3 minutos.
Orientações: Professor, leia com alunos as conclusões apresentadas e solicite seu registro.
Propósito: Concluir a aula apresentando os conceitos estudados de forma breve.
Raio X
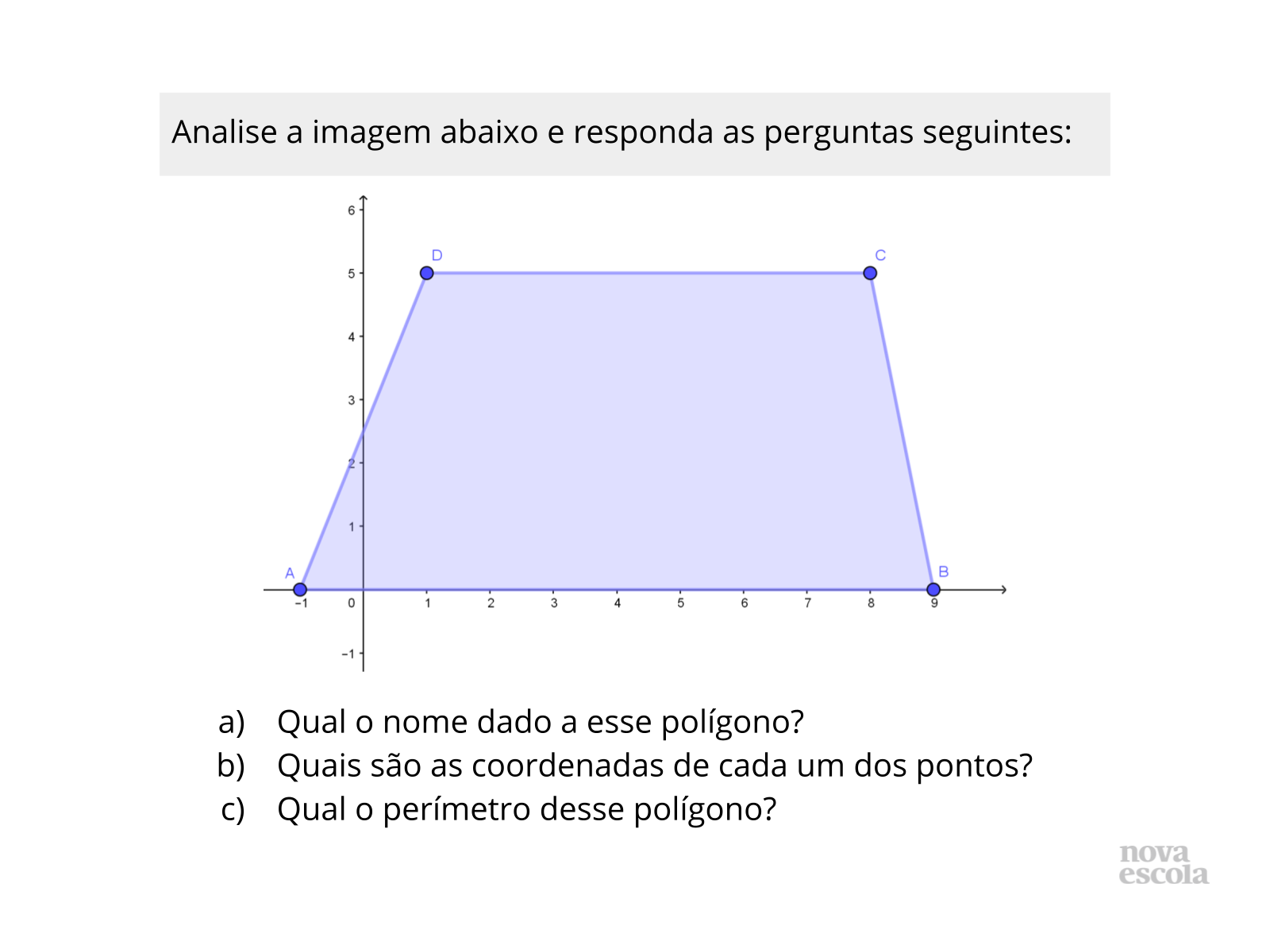
Tempo sugerido: 5 minutos.
Orientações: Circule pela sala e veja se os alunos estão realizando a atividade de forma correta. Essa atividade deve ser realizada individualmente.
Propósito: Aplicar o conhecimento em um exercício contextualizado.
Discuta com a turma:
- Quais os segmentos paralelos aos eixos?
- Qual o segmento não paralelo?
Materiais complementares:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar