Resumo da Aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Professor, leia com os alunos o objetivo da aula e garanta que saibam o significado dos termos matemáticos presentes.
Propósito: Apresentar o objetivo da aula.
Discuta com a Turma:
- O que é um plano cartesiano?
- Quais são os eixos do plano cartesiano?
- Quais são os quadrantes do plano cartesiano? Quais valores cada quadrante assume?
Aquecimento

Tempo sugerido: 10 minutos (slides 3, 4 e 5).
Orientações: Professor, apresente a afirmação aos alunos e logo em seguida distribua uma folha de malha quadriculada por aluno.
Propósito: Trabalhar o conceito de plano, ponto e segmento de reta na malha quadriculada.
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Aquecimento

Tempo sugerido: 10 minutos (slides 3, 4 e 5).
Orientações: Professor, entregue uma malha quadriculada para cada aluno e solicite que construam um plano cartesiano e identifique os pontos conforme o enunciado.
Propósito: Trabalhar o conceito de plano, ponto e segmento de reta na malha quadriculada.
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Aquecimento

Tempo sugerido: 10 minutos (slides 3, 4 e 5).
Orientações: Esse é um momento de inserir o conceito de distância entre pontos e segmento de reta. Saliente que, ao definir distâncias, o resultado obtido se trata de um valor positivo.
Propósito: Indagar aos alunos sobre a distância entre pontos.
Discuta com a turma:
- Qual a diferença entre reta e segmento de reta?
- Quais unidades de medidas podem ser usadas no cálculo de distâncias?
- Distâncias são sempre positivas?
- O que é módulo de um número?
Materiais complementares:
Aquecimento
Resolução do Aquecimento
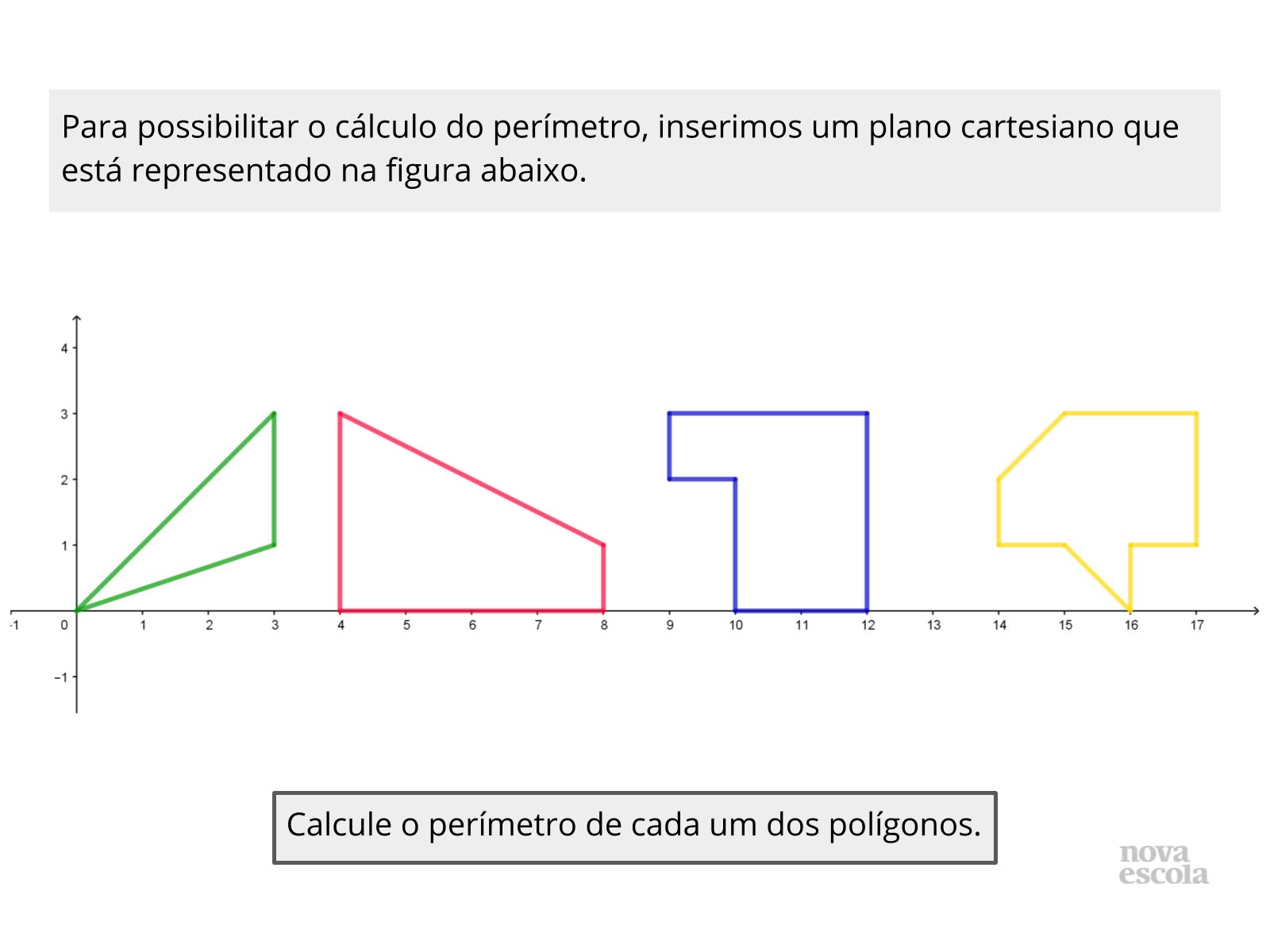
Atividade Principal

Tempo sugerido: 15 minutos (slides 6, 7 e 8).
Orientações: Professor, caminhe pela sala e observe se os alunos estão usando de forma adequada a malha quadriculada. A atividade pode ser realizada em duplas, mas cada aluno realizando sua construção.
Propósito: Trabalhar a habilidade dos alunos na definição dos pontos no plano e na percepção de cálculo da distância entre eles.
Discuta com a turma:
- Qual segmento define os catetos?
- Qual segmento define a hipotenusa?
- Por que, quando o gráfico intercepta o eixo das abscissas ou das ordenadas, um de seus valores é zero?
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
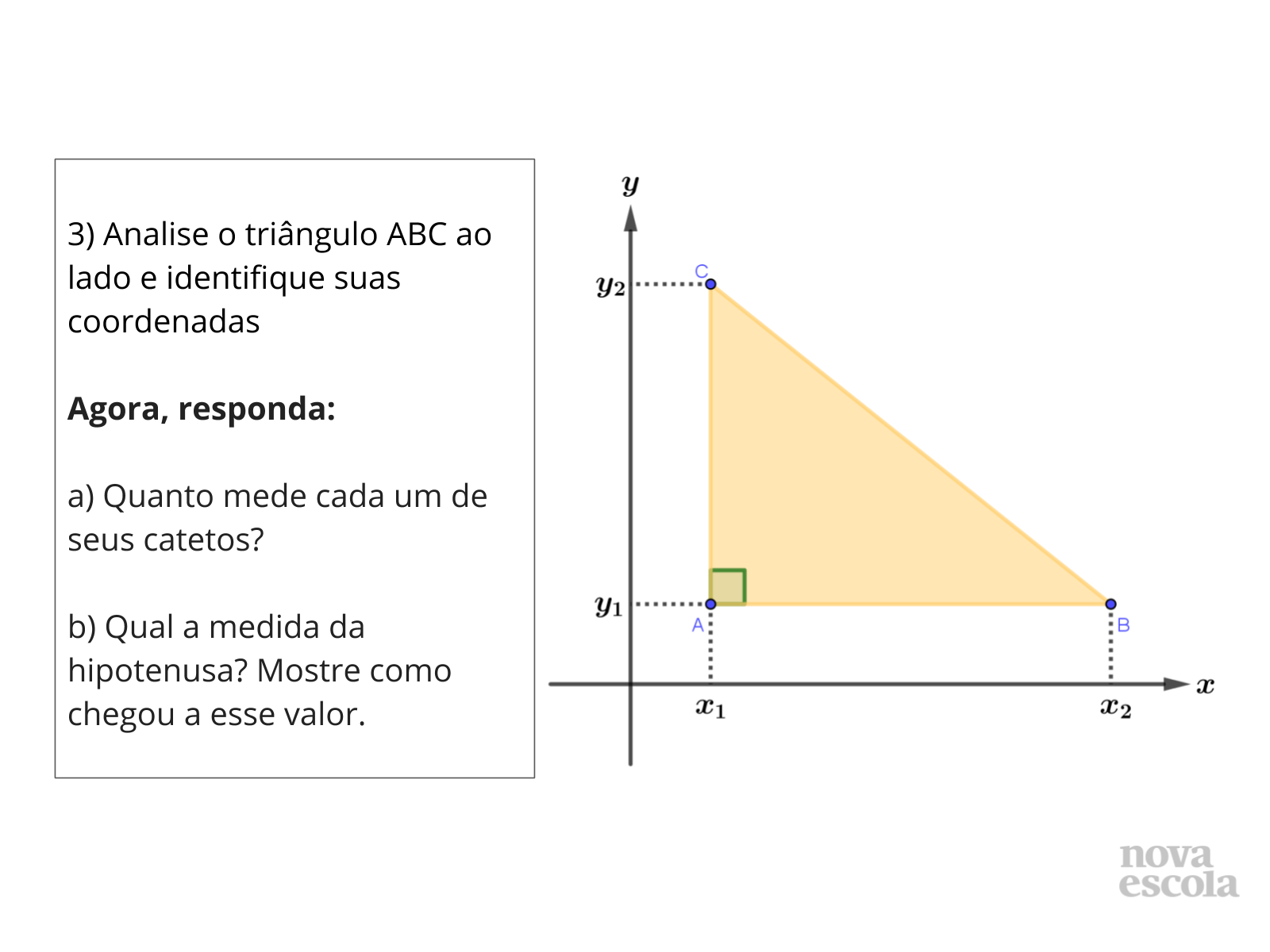
Atividade Principal

Tempo sugerido: 15 minutos (slides 6, 7 e 8).
Orientações: Professor, caminhe pela sala e observe se os alunos estão usando de forma adequada a malha quadriculada. A atividade pode ser realizada em duplas, mas cada aluno realizando sua construção.
Propósito: Trabalhar a habilidade dos alunos na definição dos pontos no plano e na percepção de cálculo da distância entre eles.
Discuta com a turma:
- Qual segmento define os catetos?
- Qual segmento define a hipotenusa?
- Qual teorema utilizamos para o cálculo da hipotenusa de um triângulo?
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
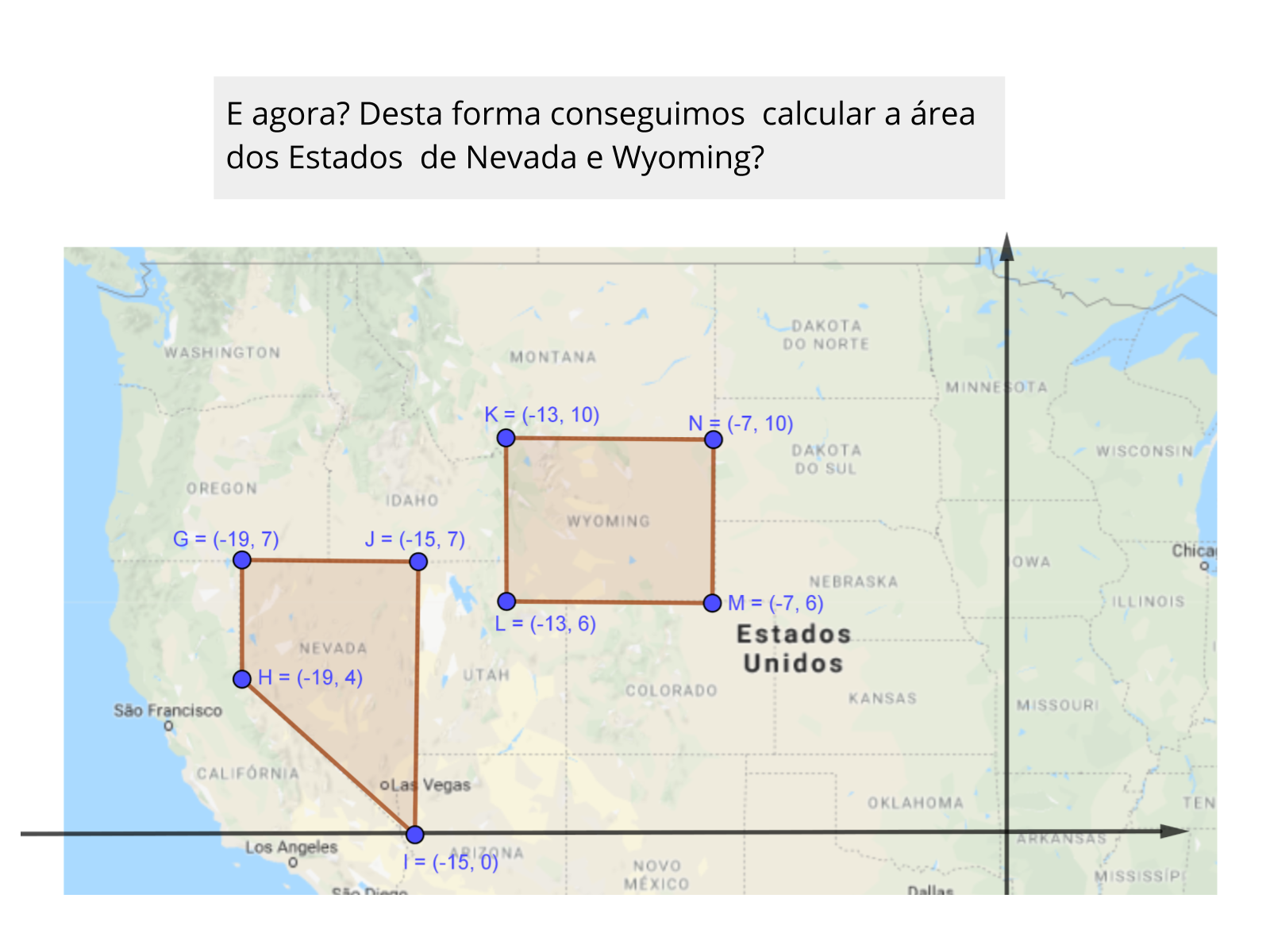
Atividade Principal
Tempo sugerido: 15 minutos (slides 6, 7 e 8).
Orientações: Professor, deixe que os alunos percebam que, para determinar a distância entre dois pontos cujo segmento é paralelo aos eixos coordenados, basta calcular a diferença entre o ponto final e o ponto inicial. E para calcular a distância de um segmento que está na diagonal, devemos aplicar o Teorema de Pitágoras.
Propósito: Trabalhar a habilidade dos alunos na definição dos pontos no plano e na percepção de cálculo da distância entre eles.
Discuta com a Turma:
- Qual o ponto final e o ponto inicial de cada segmento? Essa definição altera a medida do segmento?
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão da Solução
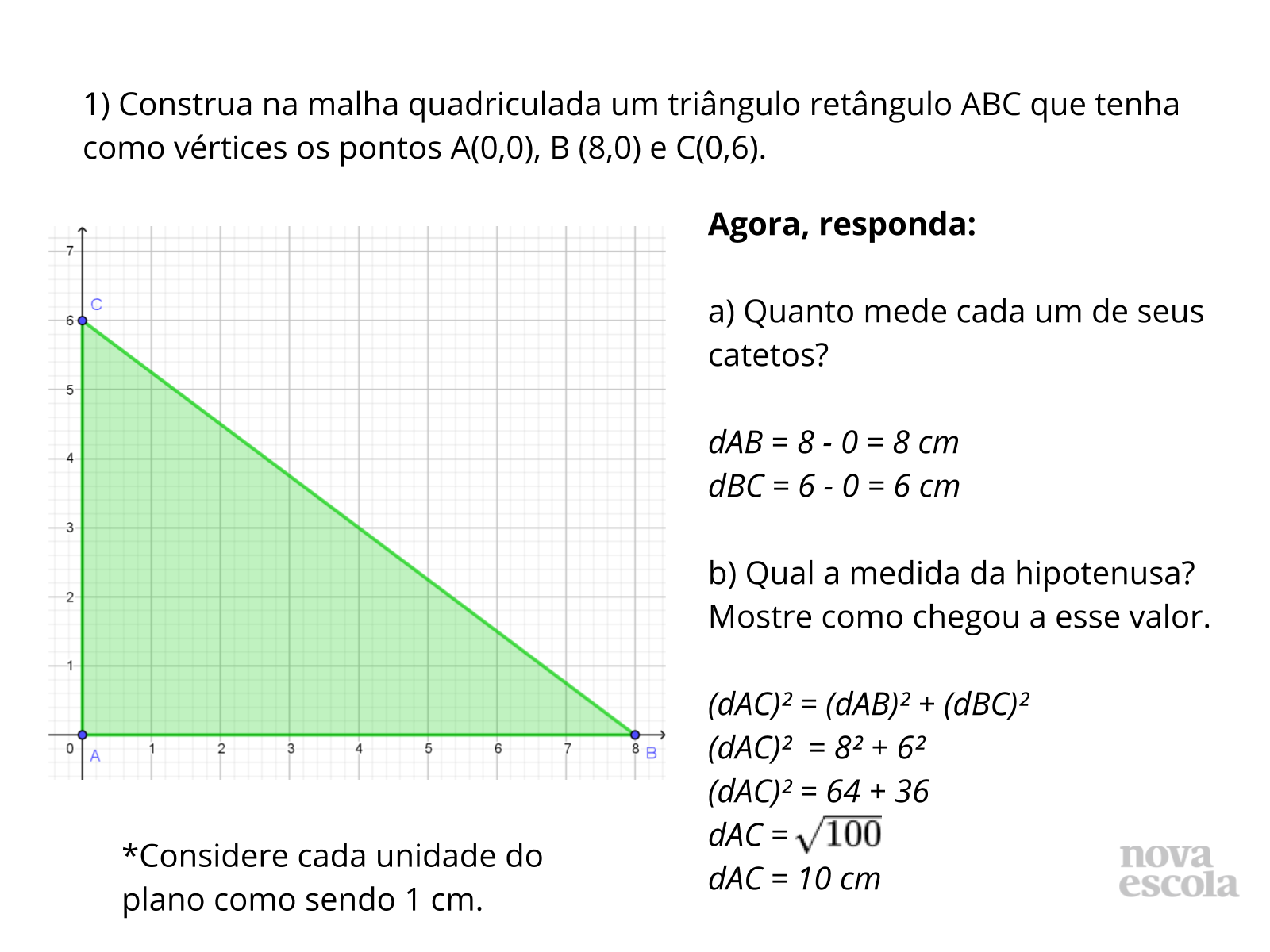
Tempo sugerido: 10 minutos (slides 9, 10 e 11).
Orientações: Professor, resolva os exercícios no quadro e diga aos alunos que confiram seus resultado. Isso validará de forma prática a aplicação deste conceito. Mostre a formação do triângulo retângulo a partir da união dos segmentos e justifique a utilização do Teorema de Pitágoras.
Propósito: Analisar junto a turma as resoluções realizadas.
Discuta com a Turma:
- Distância sempre dão resultados positivos?
- Ainda restam dúvidas?
Discussão da Solução
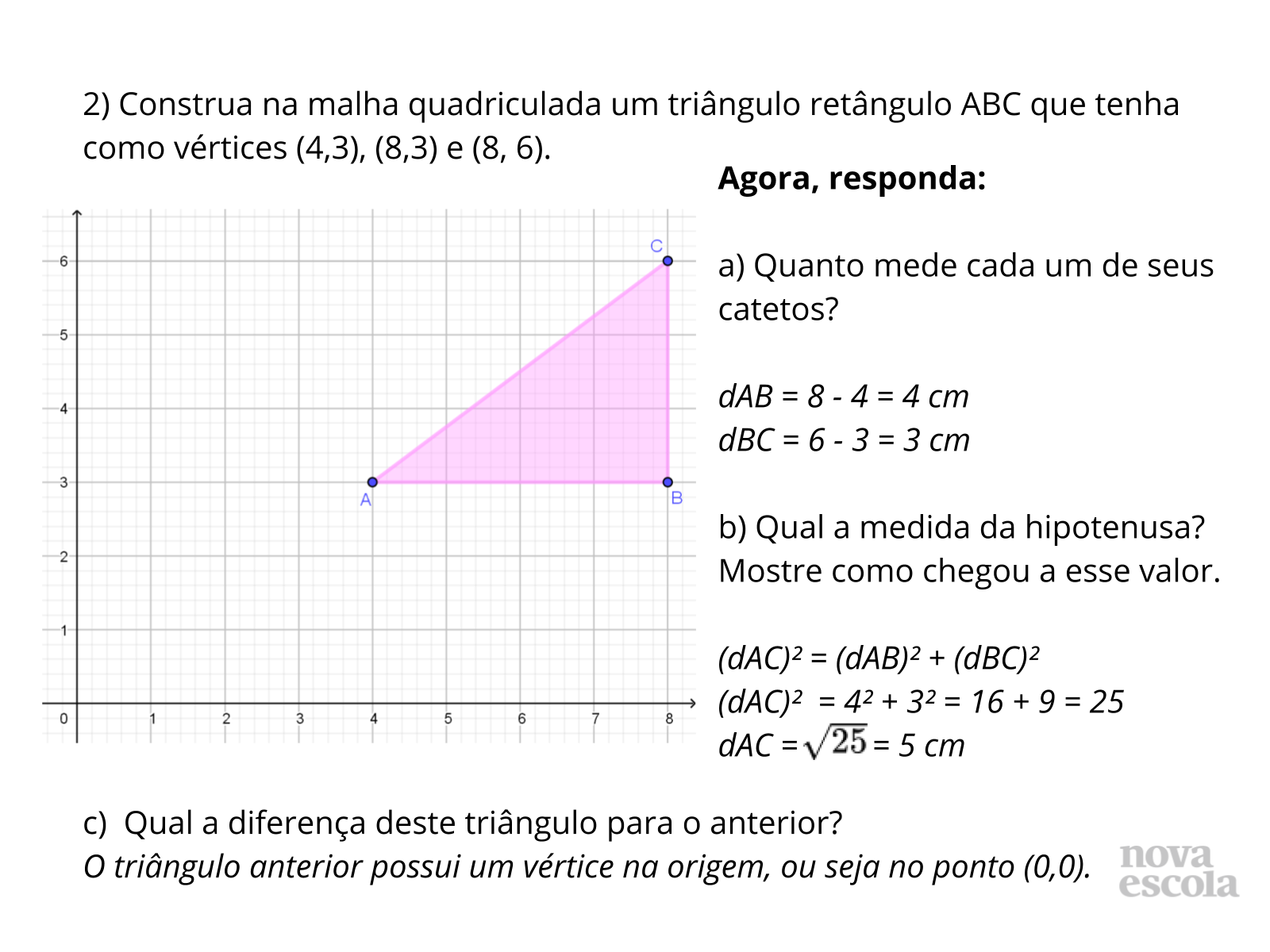
Tempo sugerido: 10 minutos (slides 9, 10 e 11).
Orientações: Professor, resolva os exercícios no quadro e diga aos alunos que confiram seus resultado. Isso validará de forma prática a aplicação deste conceito. Mostre a formação do triângulo retângulo a partir da união dos segmentos e justifique a utilização do Teorema de Pitágoras.
Propósito: Analisar junto a turma as resoluções realizadas.
Discuta com a Turma:
- Distâncias sempre dão resultados positivos?
- Ainda restam dúvidas?
Discussão da Solução
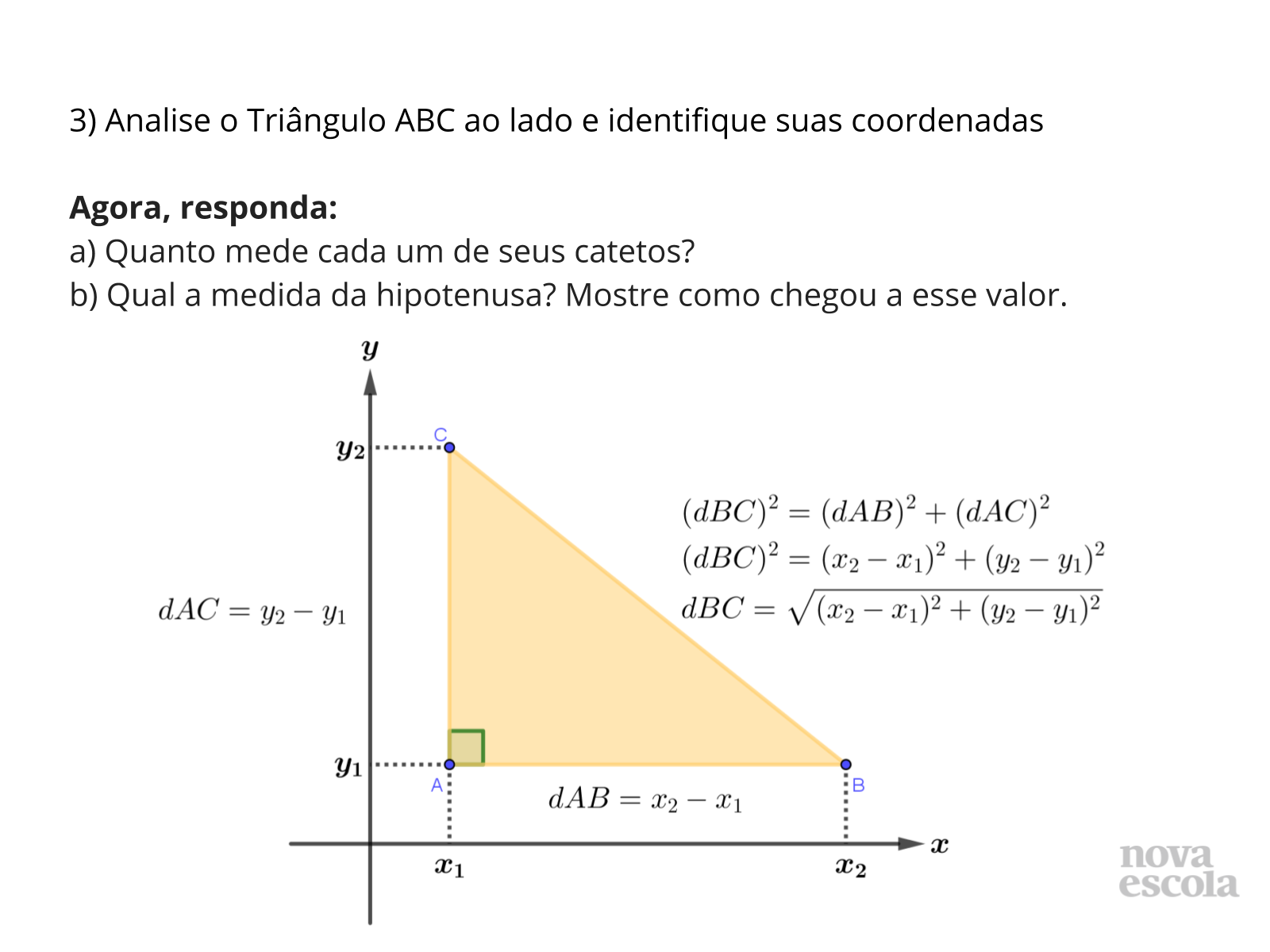
Tempo sugerido: 10 minutos (slides 9, 10 e 11).
Orientações: Professor, auxilie os alunos na percepção da generalização do cálculo da distância entre dois pontos.
Propósito: Trabalhar a habilidade dos alunos na definição dos pontos no plano e na percepção de cálculo da distância entre eles.
Discuta com a Turma:
- Quais valores as coordenadas dos pontos A, B e C podem assumir?
Sistematização do conceito

Tempo sugerido: 7 minutos.
Orientações: É importante que, junto com a turma, faça uma retomada do novos conhecimentos adquiridos. Este é momento de esclarecer qualquer dúvida que tenha ficado para os alunos. Solicite que os alunos registrem as conclusões no caderno.
Propósito: Sistematizar as aprendizagem da aula.
Discuta com a turma:
- Em algum momento é possível que o resultado da distância entre dois pontos seja negativa?
Encerramento
Tempo sugerido: 3 minutos.
Orientações: Professor, leia com alunos a conclusão apresentada e solicite seu registro.
Propósito: Concluir a aula apresentando os conceitos aprendidos de forma breve.
Raio X

Tempo sugerido: 5 minutos.
Orientações: Circule pela sala e veja se os alunos estão realizando a atividade de forma correta. Essa atividade deve ser realizada individualmente.
Propósito: Aplicar o conhecimento em um exercício contextualizado.
Discuta com a turma:
- Qual os segmentos paralelos aos eixos?
- Qual o segmento não paralelo?
Materiais complementares:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.