Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 min
Orientação: Leia, projete ou escreva na lousa.
Propósito: Apresentar o objetivo da aula para a turma.
Discuta com a turma:
Retomada

Tempo sugerido: 5 min.
Orientação: Projete, escreva na lousa ou distribua o material impresso. Lance o questionamento e permita que os alunos discutam entre si, posteriormente peça para que exponham para sala suas respostas. Anote-as na lousa em formato de tópicos, e estimule aos outros que não expuseram a apontarem se concordam ou discordam. Espera-se que os alunos já tenham o domínio e que consigam chegar a conclusão que utiliza-se o produto de probabilidades para calcular a probabilidade de eventos dependentes e independentes.
Propósito: Relembrar acerca do produto de probabilidades.
Discuta com a turma:
- No que interfere na hora do cálculo, o evento ser dependente ou independente?
Materiais complementares para impressão:
Retomada
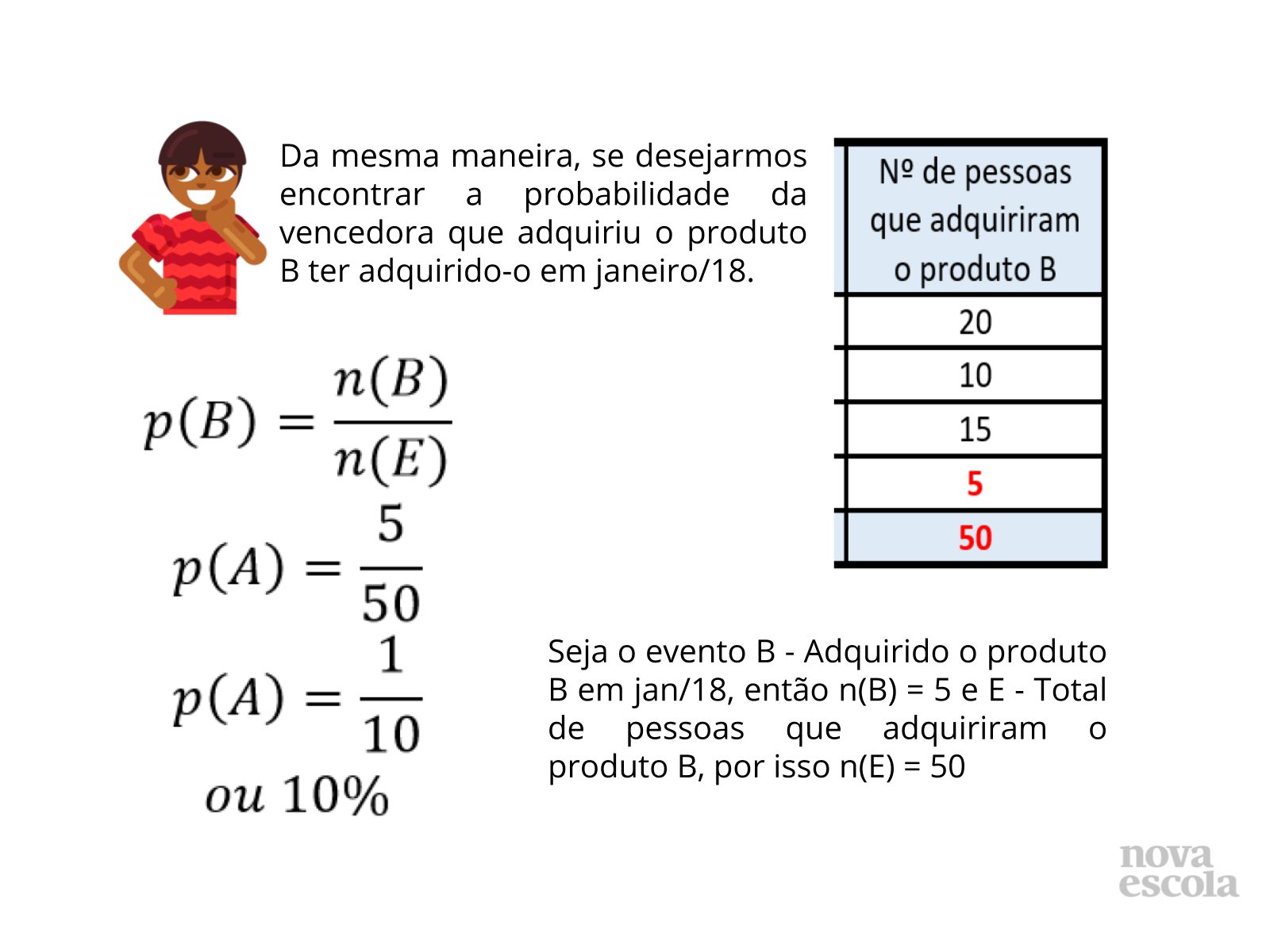
Resolução da Retomada
Atividade Principal

Tempo sugerido: 15 min
Orientação: Solicite aos alunos que reúnam-se em grupos de até três alunos. Distribua a atividade ou projete e peça para que os alunos leiam e discutam entre si. Circule pela sala observando o trabalho do grupo. Leia com atenção aos alunos as regras admitidas pela comissão. Explique que o exame antidoping é muito praticado em esportes, provavelmente já ouviram sobre isso.
Podem surgir algumas dúvidas acerca das regras que estarão detalhadas no guia de intervenções.
Propósito: Discutir formas de calcular a probabilidade de eventos independentes aplicado a um contexto.
Discuta com a turma:
- Quais são os pontos a serem levados em consideração na resolução?
- Que características determinariam a vitória da equipe A?
- Somente o último quesito “chance de vitória de A ser 30%” implicaria na vitória?
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão da Solução

Tempo sugerido: 15 min. (slides 5, 6 e 7)
Orientação: A ideia é deixar que os alunos exponham suas soluções. Observe e verifique qual foi o pensamento realizado pelo aluno e compare com a solução apresentada aqui. É muito importante que a aula seja conduzida de acordo com as respostas apresentadas pelos alunos, os slides devem ser utilizados como um roteiro. No entanto, podem surgir respostas que façam você começar pelo final da solução.
Comece questionando qual o caminho a seguir. A solução da atividade inicia-se buscando quais são as possibilidades que fariam a equipe A ser vitoriosa: A primeira opção é ambas equipes estarem limpas no exame e que o resultado da competição A saia vitoriosa, ou pensarmos na segunda opção: que A esteja “limpa” no exame e que alguém da equipe B seja pego. Não esqueça de lembrar aos alunos que a probabilidade pode ser representada por porcentagem, números decimais ou em fração. Lembrando que uma forma implica na outra.
Propósito: Apresentar uma forma de solução utilizando-se de produto e soma de probabilidades.
Discuta com a turma:
- Podemos representar probabilidades com números decimais?
Discussão da Solução

Tempo sugerido: 15 min. (slides 5, 6 e 7)
Orientação:Observe com os alunos que a pergunta “Qual a probabilidade de que ambas equipes estejam limpas e A ser vitoriosa” está relacionada com eventos simultâneos e independentes, logo basta realizarmos o produto de probabilidades. Isso se dá uma vez que a situação problema expõe que são eventos independentes. A segunda pergunta refere-se a A estar limpa, neste caso já temos calculada a probabilidade. Na segunda parte quando trata-se de B ser eliminada, é importante ressaltar aos alunos que eles podem utilizar-se de eventos complementares, ou seja, se já temos a probabilidade de B estar limpa, basta tirarmos do todo.
Propósito: Apresentar uma forma de solução utilizando-se de produto e soma de probabilidades.
Discuta com a turma:
- O que você entende por eventos complementares?
- Em probabilidade, qual é o percentual máximo?
- Então o evento complementar é aquele que somando dá 100%?
Discussão da Solução

Tempo sugerido: 15 min. (slides 5, 6 e 7)
Orientação: Observe com os alunos que estamos fazendo a união de duas probabilidades, desse modo devemos somar o resultado de ambas as opções. É importante observar que a probabilidade que foi encontrada não tem relação com a probabilidade de vitória determinada no enunciado de problema, que apenas foi uma coincidência, uma vez que estamos trabalhando com elementos aleatórios.
Propósito: Apresentar uma forma de solução utilizando-se de produto e soma de probabilidades.
Discuta com a turma:
- Existe alguma relação do valor estar próximo do enunciado? Isto é, a chance de vitória de A em um confronto direto é 30%
Encerramento
Tempo sugerido: 3 min
Orientação: Projete ou leia com os alunos, observe com eles a importância da compreensão do problema envolvido para saber como proceder no cálculo, explique que é necessário observar o que pode ou não influenciar no cálculo, quais as vertentes a serem consideradas, exigindo do estudante do que memorizar o algoritmo.
Propósito: Resumir o aprendido em aula.
Discuta com a turma:
Raio X

Tempo sugerido: 10 min.
Orientação: Professor, peça para os alunos resolverem em grupos e posteriormente discutirem as soluções com a sala.
Propósito: Aplicar os conhecimentos adquiridos na aula.
Discuta com a turma:
- Houve reposição?
- Estamos trabalhando com eventos dependentes ou independentes?
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.