Atividade Principal
Plano de Aula
Plano de aula: Classificando triângulos
Plano 4 de uma sequência de 10 planos. Veja todos os planos sobre Figuras bidimensionais: elementos e relações
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA.
Autora: Olenêva Sanches Sousa
Mentora: Paula Massi Reis Pires
Revisora Pedagógica: Eliane Zanin
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
EF5MA17: Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e desenhá-los, utilizando material de desenho ou tecnologias digitais.
Objetivos específicos
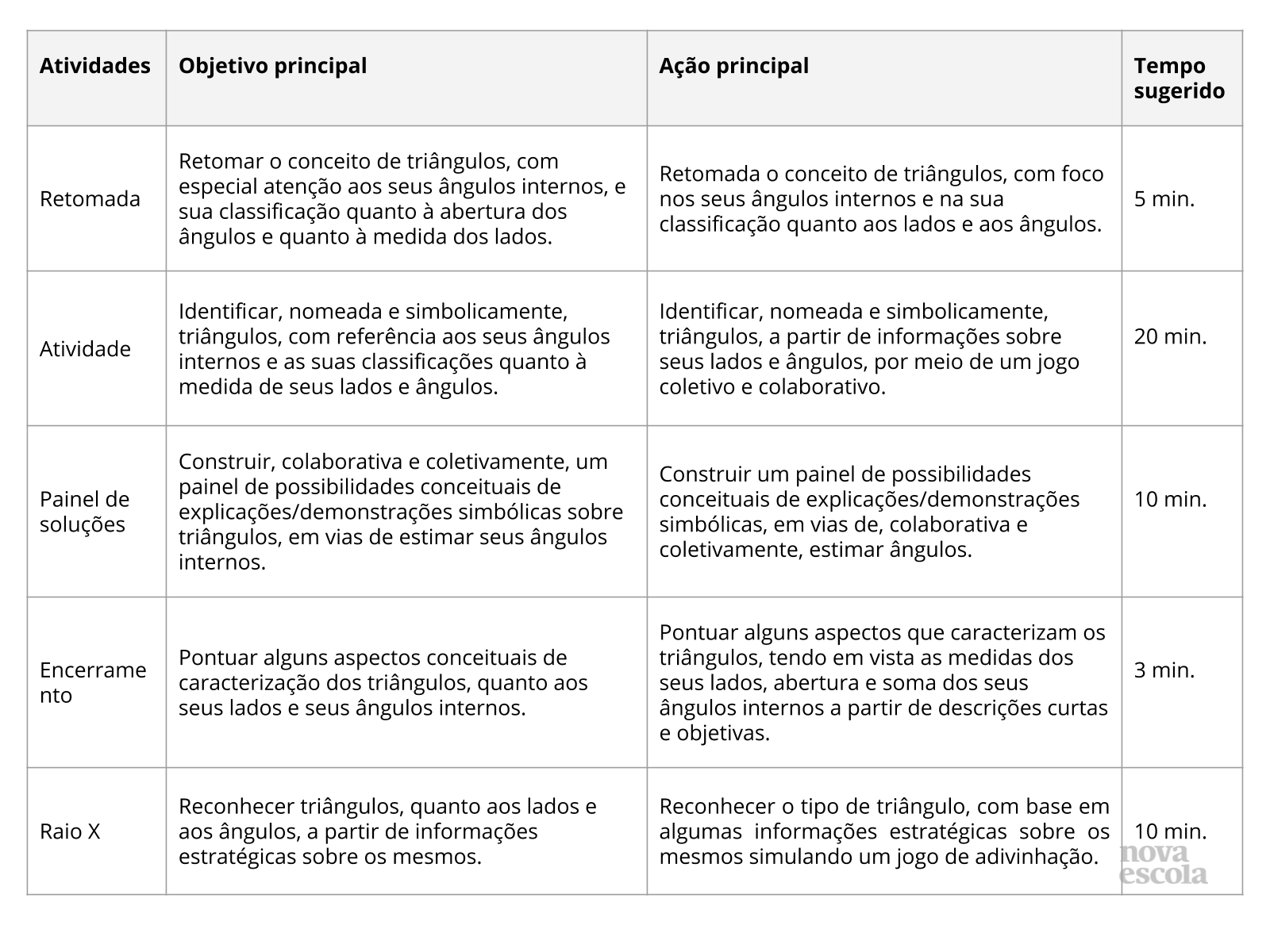
- Retomar o conceito de triângulos, com foco em seus ângulos internos e em suas classificações quanto aos ângulos e aos lados;
- Identificar, nomeada e simbolicamente, triângulos;
- Construir possibilidades conceituais de explicações/demonstrações simbólicas sobre triângulos;
- Estimar ângulos internos de triângulos.
- Pontuar aspectos conceituais de caracterização dos triângulos;
- Reconhecer triângulos, a partir de dados que os caracterizam.
Conceito-chave
Triângulo: tipos e relação aditiva de ângulos.
Recursos necessários
Recursos materiais docentes:
- Quadro e pincel;
- Atividades impressas (uma cópia por estudante);
- Datashow (opcional).
Recursos materiais discentes:
- Lápis;
- Borracha.
Habilidades BNCC:
Objetivos de aprendizagem
- Retomar o conceito de triângulos, com foco em seus ângulos internos e em suas classificações quanto aos ângulos e aos lados;
- Identificar, nomeada e simbolicamente, triângulos;
- Construir possibilidades conceituais de explicações/demonstrações simbólicas sobre triângulos;
- Estimar ângulos internos de triângulos.
- Pontuar aspectos conceituais de caracterização dos triângulos;
- Reconhecer triângulos, a partir de dados que os caracterizam.
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
- Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
- Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
- Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
- Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.”
Objetivo
Tempo sugerido: 2 minutos
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 5 minutos.(slides 3 e 4)
Orientação:
- Escreva no quadro ou projete e utilize os slides 3 e 4 como recurso motivador (abaixo, veja sugestão em Discuta com a turma) às reflexões acerca das propriedades gerais do triângulo, já estudadas, como ser polígono, número de lados e de ângulos, os elementos vértices, lados e ângulos, nomeação dos vértices e dos triângulos, classificação quanto à medida dos lados e quanto à abertura dos ângulos internos, e soma dos ângulos internos. Se necessário, complemente com desenho no quadro. Em síntese, busque fazer com que todos saibam (relembrem) o que é um triângulo e suas principais características.
- Mais questões provocadoras, acesse o Guia de Intervenções.
Propósito: Retomar o conceito de triângulos, suas características e classificações.
Discuta com a turma:
Slide 3 - Foco nos lados: Uma sugestão de mediação, tendo o conteúdo do slide 3 como recurso motivador, é: peça para que os estudantes leiam, silenciosamente, para, em seguida, utilizar cada “fala” para puxar a discussão, a exemplo de:
- Por que o triângulo rosa acha que encontrou o seu par?
- Como você classificaria este triângulo? Por quê?
- E o triângulo amarelo, azul? Por quê?
- Por que o triângulo amarelo estranha ser chamado de par do triângulo rosa?
- Por que o triângulo rosa se acha parecido com o triângulo amarelo?
- O triângulo amarelo é de dois tipos mesmo? Por quê?
- Como você justificaria essa classificação dupla do triângulo amarelo?
- Por que o triângulo azul pede respeito às suas diferenças?
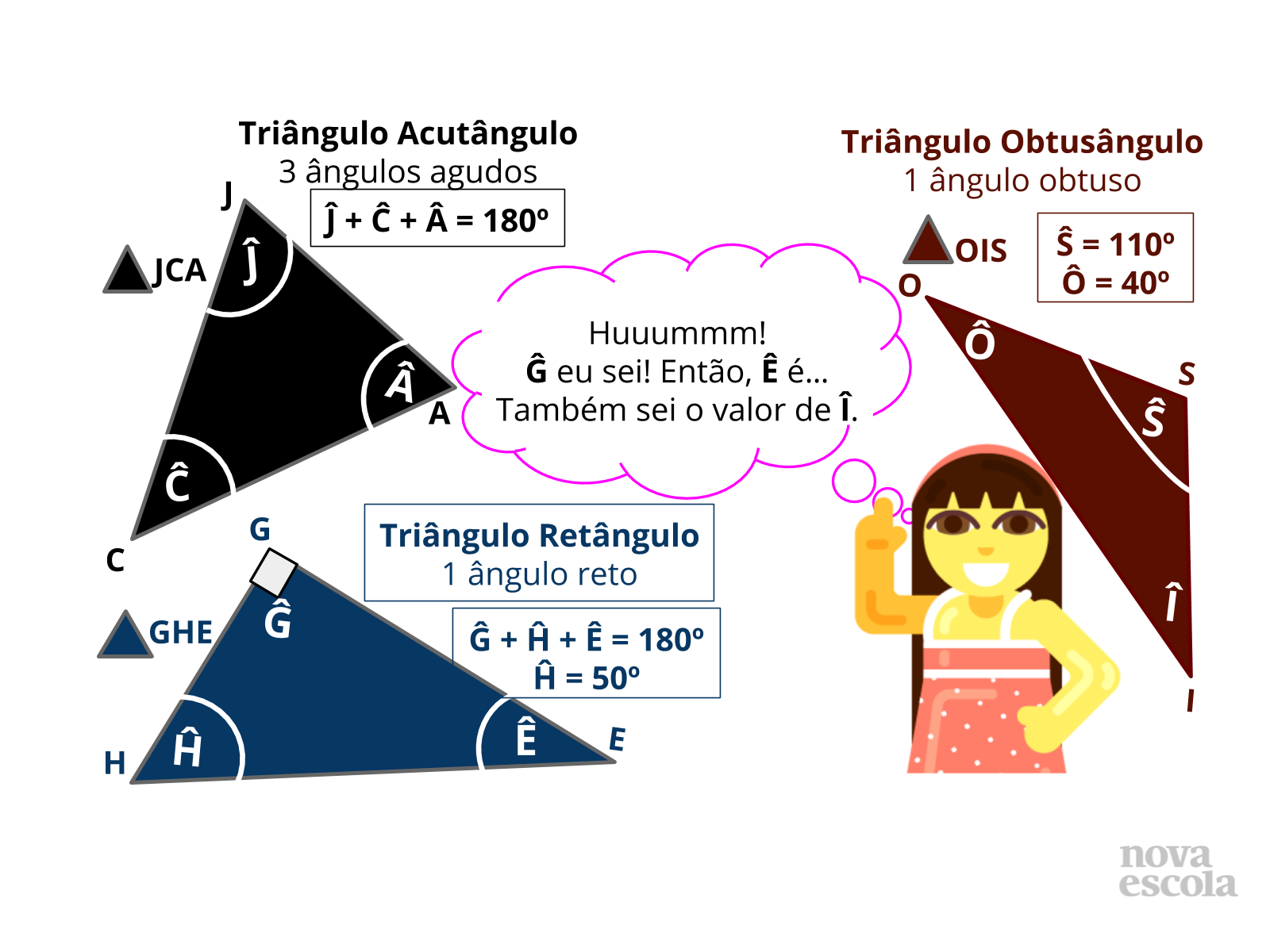
Slide 4 - Foco nos ângulos: Uma sugestão de mediação, tendo o slide 4 como recurso motivador, é: Peça para que os estudantes analisem o conteúdo do slide para puxar a discussão, a exemplo de:
- Quantos ângulos internos tem um triângulo?
- Quais os nomes dos vértices do triângulo preto? E do azul, vermelho?
- Como se chama o triângulo preto? E o azul, o marrom? Como você nomeia um triângulo?
- Qual o valor da soma das medidas dos 3 ângulos de um triângulo?
- Por que a garota sabe o valor de ?? Você também sabe? Por quê?
- No triângulo azul, qual o valor de ??
- Se você sabe o valor de ? e de ?, é possível saber o valor de Ê? Qual é este valor? Como você o encontra? Pode mostrar?
- Parece que a garota não sabe o valor de nenhum dos ângulos do triângulo preto. Você sabe? Por quê?
- É possível, calculando, saber os ângulos do triângulo preto? Como você faria para saber os valores dos seus ângulos?
- Como a garota sabe o valor de Î? Você pode demonstrar como podemos entrar este valor?
- Será que existe algum caso, no qual saber o valor de um ângulo implicaria conhecer os valores dos outros dois? Pode dar um exemplo?
- Parece que a garota não sabe o valor de nenhum dos ângulos do triângulo preto. Por quê?
Retomada
Tempo sugerido: 5 minutos.(slides 3 e 4)
Orientação:
- Escreva no quadro ou projete e utilize os slides 3 e 4 como recurso motivador (abaixo, veja sugestão em Discuta com a turma) às reflexões acerca das propriedades gerais do triângulo, já estudadas, como ser polígono, número de lados e de ângulos, os elementos vértices, lados e ângulos, nomeação dos vértices e dos triângulos, classificação quanto à medida dos lados e quanto à abertura dos ângulos internos, e soma dos ângulos internos. Se necessário, complemente com desenho no quadro. Em síntese, busque fazer com que todos saibam (relembrem) o que é um triângulo e suas principais características.
- Mais questões provocadoras, acesse o Guia de Intervenções.
Propósito: Retomar o conceito de triângulos, suas características e classificações.
Discuta com a turma:
Slide 3 - Foco nos lados: Uma sugestão de mediação, tendo o conteúdo do slide 3 como recurso motivador, é: peça para que os estudantes leiam, silenciosamente, para, em seguida, utilizar cada “fala” para puxar a discussão, a exemplo de:
- Por que o triângulo rosa acha que encontrou o seu par?
- Como você classificaria este triângulo? Por quê?
- E o triângulo amarelo, azul? Por quê?
- Por que o triângulo amarelo estranha ser chamado de par do triângulo rosa?
- Por que o triângulo rosa se acha parecido com o triângulo amarelo?
- O triângulo amarelo é de dois tipos mesmo? Por quê?
- Como você justificaria essa classificação dupla do triângulo amarelo?
- Por que o triângulo azul pede respeito às suas diferenças?
Slide 4 - Foco nos ângulos: Uma sugestão de mediação, tendo o slide 4 como recurso motivador, é: Peça para que os estudantes analisem o conteúdo do slide para puxar a discussão, a exemplo de:
- Quantos ângulos internos tem um triângulo?
- Quais os nomes dos vértices do triângulo preto? E do azul, vermelho?
- Como se chama o triângulo preto? E o azul, o marrom? Como você nomeia um triângulo?
- Qual o valor da soma das medidas dos 3 ângulos de um triângulo?
- Por que a garota sabe o valor de ?? Você também sabe? Por quê?
- No triângulo azul, qual o valor de ??
- Se você sabe o valor de ? e de ?, é possível saber o valor de Ê? Qual é este valor? Como você o encontra? Pode mostrar?
- Parece que a garota não sabe o valor de nenhum dos ângulos do triângulo preto. Você sabe? Por quê?
- É possível, calculando, saber os ângulos do triângulo preto? Como você faria para saber os valores dos seus ângulos?
- Como a garota sabe o valor de Î? Você pode demonstrar como podemos entrar este valor?
- Será que existe algum caso, no qual saber o valor de um ângulo implicaria conhecer os valores dos outros dois? Pode dar um exemplo?
- Parece que a garota não sabe o valor de nenhum dos ângulos do triângulo preto. Por quê?
Atividade Principal

Tempo sugerido: 20 minutos.( slides 5 e 6)
Orientações:
- Peça para que, silenciosamente, os estudantes leiam o slide 5. Se não puder projetar, escreva o conteúdo no quadro.
- Faça mediações sobre o diálogo do slide 5 de modo que todos entendam que desenvolverão uma atividade coletiva e colaborativa, cujas perguntas e respostas são encadeadas e sequenciadas.
- Na mediação, enfatize a última questão Quem tem?, sugerindo que algumas questões podem apresentar, propositadamente, dados incoerentes, que impliquem a inexistência de um triângulo-resposta.
- Não exceda 1 minuto nessa provocação para a Atividade Principal, contemplada no slide 5.
- Em seguida, vá para o slide 6, utilizando-o para apresentar o jogo como atividade coletiva e colaborativa.
- Explique as regras gerais do jogo Nós temos! Quem tem?, informando aos estudantes que se trata de uma adaptação para que desenvolvam uma atividade coletiva e colaborativa, na qual todos ganham, pois não há ganhadores e perdedores.
- Antes de desenvolver, pedagogicamente, qualquer jogo, você deve entender seus objetivos, regras e critérios, para que possa expor todas as informações à turma, bem como tirar as dúvidas levantadas pelos estudantes, antes de iniciá-lo. Portanto, inicie seu planejamento buscando conhecer o jogo “Eu tenho! Quem tem?”, muito usual em aulas de matemática, por sua versatilidade de aplicação ao trabalho pedagógico de vários conteúdos. Observe que, como a proposta da atividade tem caráter coletivo e colaborativo, apenas o nome do jogo foi adaptado para Nós temos! Quem tem?.
- O jogo Nós temos! Quem tem? proposto deve conter um número de cartelas igual ao número de grupos participantes. Nessa atividade, são propostas 10 cartelas (pares de proposições), sendo um par para cada um dos 10 grupos competidores. Nas cartelas sequenciadas de 1 a 10, são colocadas situações conceituais e simbólicas, referentes a um determinado triângulo, que representa o Nós temos! e, em seguida, é feita uma pergunta envolvendo uma proposta desafiadora a outro grupo, que representa o Quem tem?. A sequência de cartelas é contínua, sendo que a última (10) tem a resposta/pergunta da primeira, concluindo o jogo. Observe que o jogo deve favorecer a colaboração para resolver a questão feita pelo outro grupo e para dar uma ou mais explicações da resolução, de modo que toda a turma possa identificar os tipos de triângulos, seus elementos, nomenclatura e a propriedade da soma dos seus ângulos internos. Nesse sentido, durante o jogo, busque explorar esse espírito coletivo e colaborativo, nesse jogo que faz de todos campeões, se você fizer pequenas intervenções durante as explicações (Nós temos!) de cada grupo, como: estimule a participação de todos os membros do grupo explicador; provoque reflexões e questionamentos da turma.
- Utilize o slide 6 para explicar as regras gerais da adaptação, pontuando as 3 ações a serem desenvolvidas em grupo: 1ª) Cada grupo receberá um papel com 2 proposições, Nós temos! e Quem tem?, e deverá focar sua atenção no Nós temos!, estudando a proposição de modo exploratório, isto é, explorando todas as possibilidades que eles encontrarem para o caso do grupo. Você pode trazer o exemplo Nós temos! do slide 5 - Nós temos o triângulo equilátero - para instruí-los a fazerem uma tempestade de ideias sobre as possibilidades de perguntas sobre este triângulo, explorando lados, ângulos, classificação, etc.; 2ª) O jogo propriamente dito, isto é, uma sequência de questões (Quem tem?) e respostas (Eu tenho). Explique que você dirá quem vai iniciar o jogo (veja observação sobre isso, em seguida). Todos os grupos devem ficar atentos à questão feita e o grupo que tiver a resposta deve anunciar Nós temos…. 3ª) O grupo que anunciar que tem a resposta deve justificá-la, utilizando o estudo exploratório feito sobre a sua proposição, sendo desafiado a convencer toda a turma que sua resposta é de fato é a correta, com conceituação, demonstração e/ou outros argumentos relativos aos triângulos.
- Explicite que todos ganham com esse jogo, pois todos têm que estar atentos às perguntas, às respostas e às explicações.
- Imprima, previamente, a Atividade Principal, recortando-a em tiras, uma para cada grupo.
- Como há 10 pares de proposições, um par por grupo, utilize a Atividade Principal sem fazer alterações, se formar 10 grupos de estudantes.
- Se quiser, opte por realizar o jogo com mais de 10 grupos, bastando adicionar outros pares de proposições. Confira a Atividade Complementar, adiante, que se destina a você conhecer melhor o jogo Eu tenho! Quem tem?
- Utilizando os 10 pares propostos, após a distribuição, sugerimos que você destine 5 minutos para que os grupos façam o estudo exploratório da proposição Nós Temos!, que têm em mãos.
- Cronometre o tempo, de modo que todos tenham mesma oportunidade.
Propósito: Identificar, nomeada e simbolicamente, triângulos, a partir de informações sobre seus lados e ângulos
Discuta com a turma:
- Como você nomeia um triângulo?
- Quais os ângulos internos de um triângulo?
- Você sabe qual o valor da soma dos ângulos internos de um triângulo?
- Por que um triângulo pode ser classificado de mais de um modo?
- Você pode dar um exemplo de como isso pode ocorrer?
- Você saberia o valor de algum dos ângulos deste triângulo?
- Se o exemplo for um triângulo retângulo, você sabe o valor deste ângulo aqui? Quanto os outros dois valem juntos?
- Se esses lados são iguais, o que você poderia me dizer sobre esses dois ângulos?
- E o triângulo equilátero, como são os seus lados? E os seus ângulos?
- Em relação aos ângulos, qual a condição para a existência de um triângulo?
- Outras provocações, confira o Guia de Intervenção.
Materiais complementares:
Atividade Complementar ao Professor:
- Para conhecer um pouco sobre o recurso pedagógico dos jogos na Educação Matemática e sobre o jogo “Eu tenho! Quem tem?”, sugerimos a leitura desse artigo, de autoria de duas professoras do Rio Grande do Sul e publicado nos anais do VIII Encontro Nacional de Educação Matemática, em Pernambuco, promovido pela Sociedade Brasileira de Educação Matemática (SBEM): http://www.sbembrasil.org.br/files/viii/pdf/03/MC41839641053.pdf
Atividade Principal

Tempo sugerido: 20 minutos.( slides 5 e 6)
Orientações:
- Peça para que, silenciosamente, os estudantes leiam o slide 5. Se não puder projetar, escreva o conteúdo no quadro.
- Faça mediações sobre o diálogo do slide 5 de modo que todos entendam que desenvolverão uma atividade coletiva e colaborativa, cujas perguntas e respostas são encadeadas e sequenciadas.
- Na mediação, enfatize a última questão Quem tem?, sugerindo que algumas questões podem apresentar, propositadamente, dados incoerentes, que impliquem a inexistência de um triângulo-resposta.
- Não exceda 1 minuto nessa provocação para a Atividade Principal, contemplada no slide 5.
- Em seguida, vá para o slide 6, utilizando-o para apresentar o jogo como atividade coletiva e colaborativa.
- Explique as regras gerais do jogo Nós temos! Quem tem?, informando aos estudantes que se trata de uma adaptação para que desenvolvam uma atividade coletiva e colaborativa, na qual todos ganham, pois não há ganhadores e perdedores.
- Antes de desenvolver, pedagogicamente, qualquer jogo, você deve entender seus objetivos, regras e critérios, para que possa expor todas as informações à turma, bem como tirar as dúvidas levantadas pelos estudantes, antes de iniciá-lo. Portanto, inicie seu planejamento buscando conhecer o jogo “Eu tenho! Quem tem?”, muito usual em aulas de matemática, por sua versatilidade de aplicação ao trabalho pedagógico de vários conteúdos. Observe que, como a proposta da atividade tem caráter coletivo e colaborativo, apenas o nome do jogo foi adaptado para Nós temos! Quem tem?.
- O jogo Nós temos! Quem tem? proposto deve conter um número de cartelas igual ao número de grupos participantes. Nessa atividade, são propostas 10 cartelas (pares de proposições), sendo um par para cada um dos 10 grupos competidores. Nas cartelas sequenciadas de 1 a 10, são colocadas situações conceituais e simbólicas, referentes a um determinado triângulo, que representa o Nós temos! e, em seguida, é feita uma pergunta envolvendo uma proposta desafiadora a outro grupo, que representa o Quem tem?. A sequência de cartelas é contínua, sendo que a última (10) tem a resposta/pergunta da primeira, concluindo o jogo. Observe que o jogo deve favorecer a colaboração para resolver a questão feita pelo outro grupo e para dar uma ou mais explicações da resolução, de modo que toda a turma possa identificar os tipos de triângulos, seus elementos, nomenclatura e a propriedade da soma dos seus ângulos internos. Nesse sentido, durante o jogo, busque explorar esse espírito coletivo e colaborativo, nesse jogo que faz de todos campeões, se você fizer pequenas intervenções durante as explicações (Nós temos!) de cada grupo, como: estimule a participação de todos os membros do grupo explicador; provoque reflexões e questionamentos da turma.
- Utilize o slide 6 para explicar as regras gerais da adaptação, pontuando as 3 ações a serem desenvolvidas em grupo: 1ª) Cada grupo receberá um papel com 2 proposições, Nós temos! e Quem tem?, e deverá focar sua atenção no Nós temos!, estudando a proposição de modo exploratório, isto é, explorando todas as possibilidades que eles encontrarem para o caso do grupo. Você pode trazer o exemplo Nós temos! do slide 5 - Nós temos o triângulo equilátero - para instruí-los a fazerem uma tempestade de ideias sobre as possibilidades de perguntas sobre este triângulo, explorando lados, ângulos, classificação, etc.; 2ª) O jogo propriamente dito, isto é, uma sequência de questões (Quem tem?) e respostas (Eu tenho). Explique que você dirá quem vai iniciar o jogo (veja observação sobre isso, em seguida). Todos os grupos devem ficar atentos à questão feita e o grupo que tiver a resposta deve anunciar Nós temos…. 3ª) O grupo que anunciar que tem a resposta deve justificá-la, utilizando o estudo exploratório feito sobre a sua proposição, sendo desafiado a convencer toda a turma que sua resposta é de fato é a correta, com conceituação, demonstração e/ou outros argumentos relativos aos triângulos.
- Explicite que todos ganham com esse jogo, pois todos têm que estar atentos às perguntas, às respostas e às explicações.
- Imprima, previamente, a Atividade Principal, recortando-a em tiras, uma para cada grupo.
- Como há 10 pares de proposições, um par por grupo, utilize a Atividade Principal sem fazer alterações, se formar 10 grupos de estudantes.
- Se quiser, opte por realizar o jogo com mais de 10 grupos, bastando adicionar outros pares de proposições. Confira a Atividade Complementar, adiante, que se destina a você conhecer melhor o jogo Eu tenho! Quem tem?
- Utilizando os 10 pares propostos, após a distribuição, sugerimos que você destine 5 minutos para que os grupos façam o estudo exploratório da proposição Nós Temos!, que têm em mãos.
- Cronometre o tempo, de modo que todos tenham mesma oportunidade.
Propósito: Identificar, nomeada e simbolicamente, triângulos, a partir de informações sobre seus lados e ângulos
Discuta com a turma:
- Como você nomeia um triângulo?
- Quais os ângulos internos de um triângulo?
- Você sabe qual o valor da soma dos ângulos internos de um triângulo?
- Por que um triângulo pode ser classificado de mais de um modo?
- Você pode dar um exemplo de como isso pode ocorrer?
- Você saberia o valor de algum dos ângulos deste triângulo?
- Se o exemplo for um triângulo retângulo, você sabe o valor deste ângulo aqui? Quanto os outros dois valem juntos?
- Se esses lados são iguais, o que você poderia me dizer sobre esses dois ângulos?
- E o triângulo equilátero, como são os seus lados? E os seus ângulos?
- Em relação aos ângulos, qual a condição para a existência de um triângulo?
- Outras provocações, confira o Guia de Intervenção.
Discussão das soluções
Tempo sugerido: 10 minutos.( slides 7 e 8)
Orientações: A resolução das questões propostas na atividade está no próprio jogo, no entanto crie oportunidade para construir, colaborativa e coletivamente, um painel de possibilidades conceituais de explicações e demonstrações simbólicas sobre triângulos, e de estimar seus ângulos internos. Para isso, os alunos devem compartilhar a participação no jogo e contar como foi que pensaram na respostas para descobrir os ângulos dos triângulos. Peça que falem para os colegas as descobertas.Para a estimativa dos ângulos, é importante que todos saibam classificar os triângulos, pois a classificação é uma referência para uma boa estimativa, por isso:
- Utilize os triângulos e as falas do slide 7 para provocar reflexões.
- Não ultrapasse 1 minuto no slide 7.
- Veja, mais abaixo, em Discuta com a turma, algumas provocações pertinentes.
Propósito: Construir, um painel de possibilidades conceituais de explicações e demonstrações simbólicas sobre triângulos e de como estimar seus ângulos internos.
Discuta com a turma:
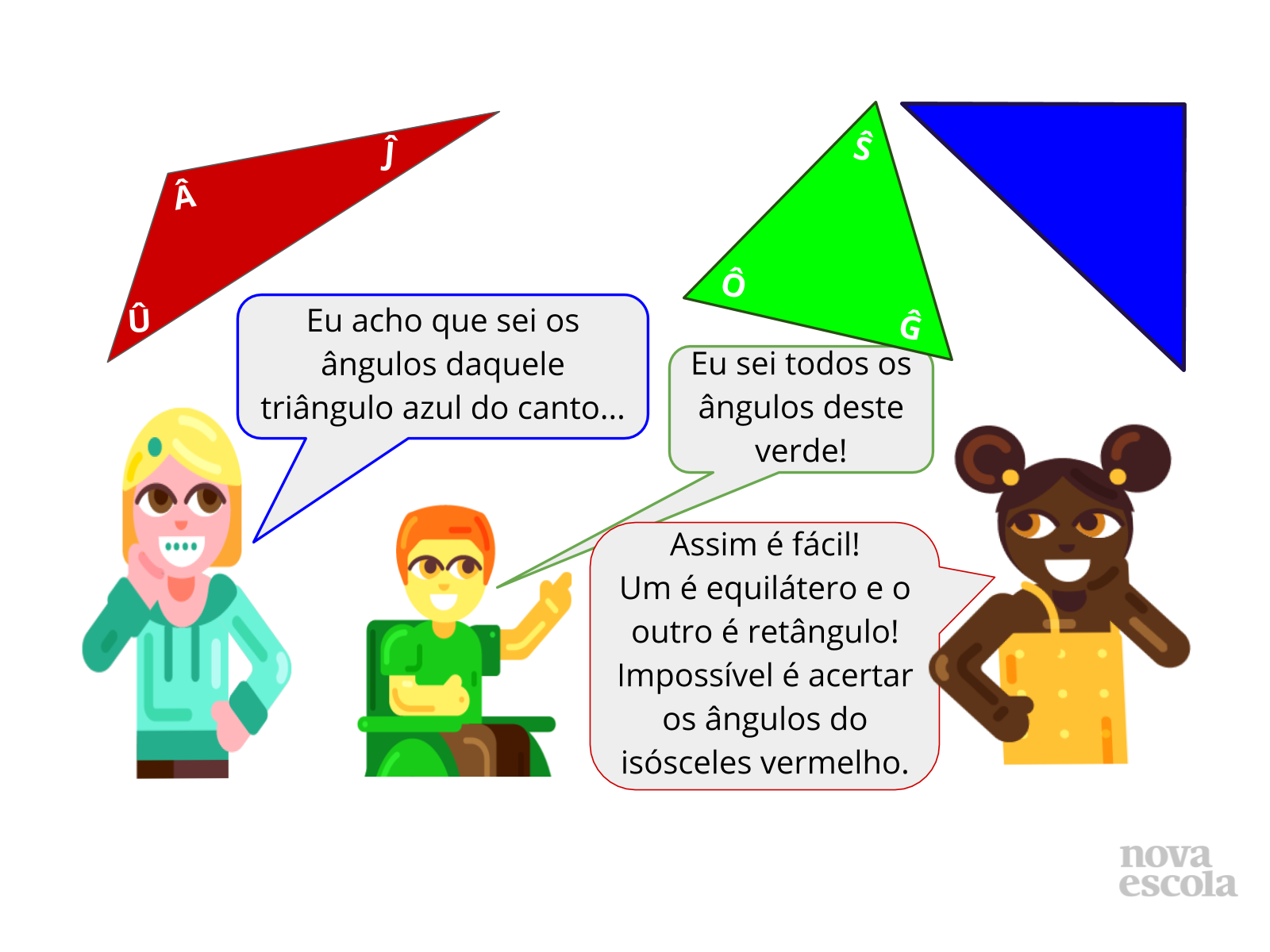
- Slide 7 - utilize-o (triângulos e falas) para as provocações prévias à atividade.
- Por que se pode saber o valor de todos os ângulos do triângulo azul do canto superior direito?
- Qual o ângulo de referência deste triângulo azul?
- Como podemos classificar este triângulo?
- Caberia outra classificação para este triângulo?
- Onde está o seu ângulo reto?
- Qual o valor do ângulo reto?
- Como é possível estimar o valor dos outros dois ângulos?
- Que referência tomamos para inferir que os dois outros ângulos têm mesma medida?
- Qual seria essa medida? Por quê?
- Por que é possível saber o valor dos ângulos do triângulo verde?
- Como você classifica este triângulo? Por quê?
- Qual o valor de cada ângulo deste triângulo?
- Por que é impossível estimar as medidas dos ângulos do triângulo vermelho?
- O que você sugere fazer para conhecer os ângulos deste triângulo?
- Slide 8 - utilize este slide para fazer as estimativas dos ângulos.
- Questione se há algum triângulo, cujos 3 lados podem ser estimados. É esperado que seja identificado o equilátero e o retângulo isósceles.
- É esperado, também, que os estudantes questionem a impossibilidade de identificação dos demais isósceles e dos escalenos. Nesses casos, faça uma estimativa inicial ou meça um dos ângulos com a ajuda de um transferidor, para questionar sobre a estimativa dos outros dois. É esperado que surjam estimativas para os ângulos iguais dos isósceles e que os estudantes deem valores para os dos escalenos. Você também pode medir mais um dos ângulos dos escalenos e pedir para que calculem o terceiro.
- Vá fazendo mediações de modo que cada ângulo seja identificado e discutida a sua identificação.
Material Complementar:
Discussão das soluções

Tempo sugerido: 10 minutos.( slides 7 e 8)
Orientações: A resolução das questões propostas na atividade está no próprio jogo, no entanto crie oportunidade para construir, colaborativa e coletivamente, um painel de possibilidades conceituais de explicações e demonstrações simbólicas sobre triângulos, e de estimar seus ângulos internos. Para isso, os alunos devem compartilhar a participação no jogo e contar como foi que pensaram na respostas para descobrir os ângulos dos triângulos. Peça que falem para os colegas as descobertas.Para a estimativa dos ângulos, é importante que todos saibam classificar os triângulos, pois a classificação é uma referência para uma boa estimativa, por isso:
- Utilize os triângulos e as falas do slide 7 para provocar reflexões.
- Não ultrapasse 1 minuto no slide 7.
- Veja, mais abaixo, em Discuta com a turma, algumas provocações pertinentes.
Propósito: Construir, um painel de possibilidades conceituais de explicações e demonstrações simbólicas sobre triângulos e de como estimar seus ângulos internos.
Discuta com a turma:
- Slide 7 - utilize-o (triângulos e falas) para as provocações prévias à atividade.
- Por que se pode saber o valor de todos os ângulos do triângulo azul do canto superior direito?
- Qual o ângulo de referência deste triângulo azul?
- Como podemos classificar este triângulo?
- Caberia outra classificação para este triângulo?
- Onde está o seu ângulo reto?
- Qual o valor do ângulo reto?
- Como é possível estimar o valor dos outros dois ângulos?
- Que referência tomamos para inferir que os dois outros ângulos têm mesma medida?
- Qual seria essa medida? Por quê?
- Por que é possível saber o valor dos ângulos do triângulo verde?
- Como você classifica este triângulo? Por quê?
- Qual o valor de cada ângulo deste triângulo?
- Por que é impossível estimar as medidas dos ângulos do triângulo vermelho?
- O que você sugere fazer para conhecer os ângulos deste triângulo?
- Slide 8 - utilize este slide para fazer as estimativas dos ângulos.
- Questione se há algum triângulo, cujos 3 lados podem ser estimados. É esperado que seja identificado o equilátero e o retângulo isósceles.
- É esperado, também, que os estudantes questionem a impossibilidade de identificação dos demais isósceles e dos escalenos. Nesses casos, faça uma estimativa inicial ou meça um dos ângulos com a ajuda de um transferidor, para questionar sobre a estimativa dos outros dois. É esperado que surjam estimativas para os ângulos iguais dos isósceles e que os estudantes deem valores para os dos escalenos. Você também pode medir mais um dos ângulos dos escalenos e pedir para que calculem o terceiro.
- Vá fazendo mediações de modo que cada ângulo seja identificado e discutida a sua identificação.
Encerramento
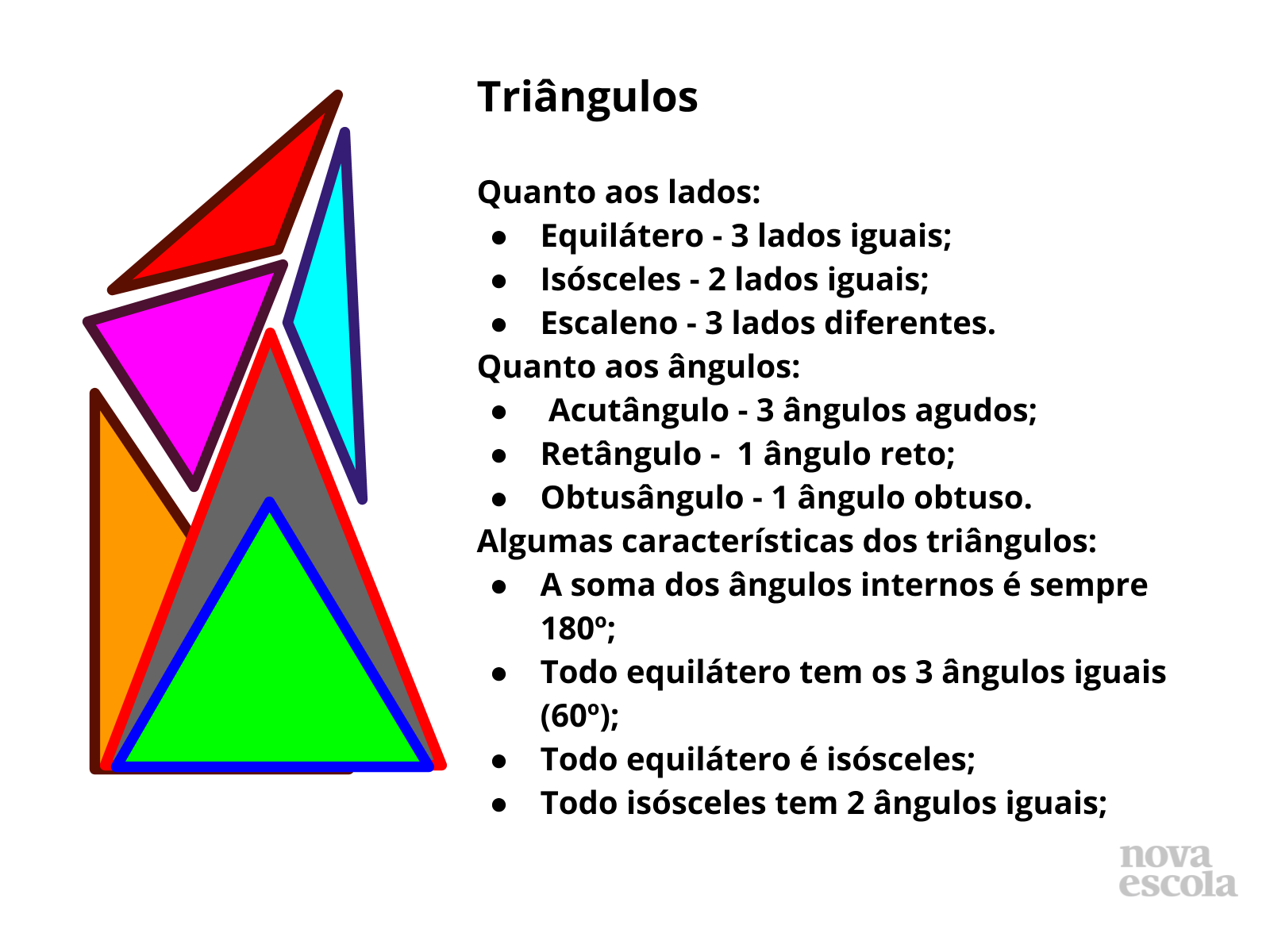
Tempo sugerido: 3 minutos.
Orientações: Este silde pontua o conteúdo trabalhado e sua apresentação deve ser muito breve, mas busque enfatizar. A partir de descrições curtas e objetivas, pontuar alguns aspectos que caracterizam os triângulos, tendo em vista as medidas dos seus lados, abertura e soma dos seus ângulos internos.
- Os ângulos internos no triângulo exposto.
- Os ângulos internos, unidos pelos vértices, somando o ângulo raso.
- A expressão algébrica que explicita a relação aditiva entre os ângulos internos desse triângulo.
- A generalização de que a soma dos ângulos do triângulo é sempre 180º.
Propósito: Sintetizar, de modo ilustrativo e algébrico, o conteúdo trabalhado.
Raio X

Tempo sugerido: 10 minutos. (slides 10 e 11)
Orientações:
- O slide 10 visa à sensibilização para a avaliação, uma simulação de um jogo de adivinhação do tipo de triângulos, com base em informações estratégicas sobre os mesmos.
- Utilize o slide 10 para explicar a atividade, aproveitando o momento para fazer uma breve mediação da “adivinhação” em jogo.
- Não estenda mais de 1 min no slide 10.
- Sem muito rigor na organização da sala, peça aos estudantes para se afastarem ou se arrumarem separadamente, porque farão uma atividade que exigirá deles reflexão, atenção e conhecimento sobre soma de ângulos e tipos de triângulos, ou imprima previamente a atividade (slide 11) para que seja realizada individualmente.
Propósito: Demonstrar conhecimentos sobre triângulos, tipos, relação aditiva entre ângulos internos.
Discuta com a turma:
- Faça provocações de modo que o estudante seja levado a refletir sobre o porquê da adivinhação. Diversas provocações estão disponíveis no Guia de Intervenção.
Materiais complementares :
Raio X

Tempo sugerido: 10 minutos. (slides 10 e 11)
Orientações:
- O slide 10 visa à sensibilização para a avaliação, uma simulação de um jogo de adivinhação do tipo de triângulos, com base em informações estratégicas sobre os mesmos.
- Utilize o slide 10 para explicar a atividade, aproveitando o momento para fazer uma breve mediação da “adivinhação” em jogo.
- Não estenda mais de 1 min no slide 10.
- Sem muito rigor na organização da sala, peça aos estudantes para se afastarem ou se arrumarem separadamente, porque farão uma atividade que exigirá deles reflexão, atenção e conhecimento sobre soma de ângulos e tipos de triângulos, ou imprima previamente a atividade (slide 11) para que seja realizada individualmente.
Propósito: Demonstrar conhecimentos sobre triângulos, tipos, relação aditiva entre ângulos internos.
Discuta com a turma:
- Faça provocações de modo que o estudante seja levado a refletir sobre o porquê da adivinhação. Diversas provocações estão disponíveis no Guia de Intervenção.
Para os Alunos
Para o Professor
Sugestão de adaptação para ensino remoto
Código do plano MAT5_17GEO04
Recursos
- Necessários: -
- Opcionais: -
Para este plano, foque na etapa Atividade principal e Encerramento
Atividade principal
Professor(a), você pode realizar a Atividade principal deste plano com seus alunos seja em uma aula síncrona ou assíncrona. Compartilhe com a turma o documento que possui as indicações de frases para o jogo “Nós temos! Quem tem?”, você a encontra aqui: https://nova-escola-producao.s3.amazonaws.com/MR2paSTQSrnhy5fT9gV5CR8U58XZHsJvg3qfw5vv7qGB7TVaJ7Br6uB5pJxh/ativaula-mat5-17geo04.pdf. O jogo não precisa ser realizado da forma proposta. Você pode solicitar que os estudantes copiem as perguntas (Quem tem) em seus cadernos, e então respondam de acordo com as afirmações (Nós temos) presentes na primeira coluna da tabela.
Encerramento
Professor(a), solicite que os alunos registrem em seus cadernos a conclusão que chegaram em relação à classificação dos triângulos de acordo com as medidas de seus lados, de seus ângulos e em relação à soma dos ângulos internos de seus ângulos internos. Caso considere viável, compartilhe com os estudantes os slides presentes nesta etapa do plano de aula. Compartilhe com os estudantes a construção do GeoGebra (https://www.geogebra.org/m/MSYKSD6w) e solicite que eles a explorem. A experimentação com o GeoGebra pode ajudar a concluir que a soma dos ângulos internos de um triângulo é sempre 180º.
Raio X
O problema proposto no Raio X pode ser enviado aos alunos e solicitado como uma “tarefa” a ser entregue em momento a ser combinado com a turma. Solicite que os alunos reproduzam as afirmações em seus cadernos e complete os espaços com suas respostas.
Convite às famílias
Professor(a), sugira que os alunos socializem com seus familiares o que aprenderam nesta aula sobre característica de triângulos. Uma sugestão de atividade é que os alunos convidem seus familiares a jogarem “Nós temos! Quem tem?”.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA.
Autora: Olenêva Sanches Sousa
Mentora: Paula Massi Reis Pires
Revisora Pedagógica: Eliane Zanin
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
EF5MA17: Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e desenhá-los, utilizando material de desenho ou tecnologias digitais.
Objetivos específicos
- Retomar o conceito de triângulos, com foco em seus ângulos internos e em suas classificações quanto aos ângulos e aos lados;
- Identificar, nomeada e simbolicamente, triângulos;
- Construir possibilidades conceituais de explicações/demonstrações simbólicas sobre triângulos;
- Estimar ângulos internos de triângulos.
- Pontuar aspectos conceituais de caracterização dos triângulos;
- Reconhecer triângulos, a partir de dados que os caracterizam.
Conceito-chave
Triângulo: tipos e relação aditiva de ângulos.
Recursos necessários
Recursos materiais docentes:
- Quadro e pincel;
- Atividades impressas (uma cópia por estudante);
- Datashow (opcional).
Recursos materiais discentes:
- Lápis;
- Borracha.