Atividade principal
Plano de Aula
Plano de aula: O Tangram e as relações métricas.
Plano 7 de uma sequência de 10 planos. Veja todos os planos sobre Relações métricas no triângulo retângulo
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Flávia Adolf Lutz Keller
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
EF09MA13 - Demonstrar relações métricas do triângulo retângulo.
Objetivos específicos
Utilizar o Tangram para verificar as relações métricas em triângulos retângulos.
Verificar algumas relações específicas em triângulos retângulos isósceles.
Conceito-chave
Relações métricas, triângulo isósceles, tangram.
Recursos necessários
Um tangram por dupla. Se a escola não tiver jogos disponíveis, pode ser colado e recortado em uma cartolina ou papel mais duro (papelão, por exemplo). O modelo para recorte encontra-se no documento ativretom_MAT9_GEO07.
Habilidades BNCC:
Objetivos de aprendizagem
Utilizar o Tangram para verificar as relações métricas em triângulos retângulos.
Verificar algumas relações específicas em triângulos retângulos isósceles.
Resumo da aula
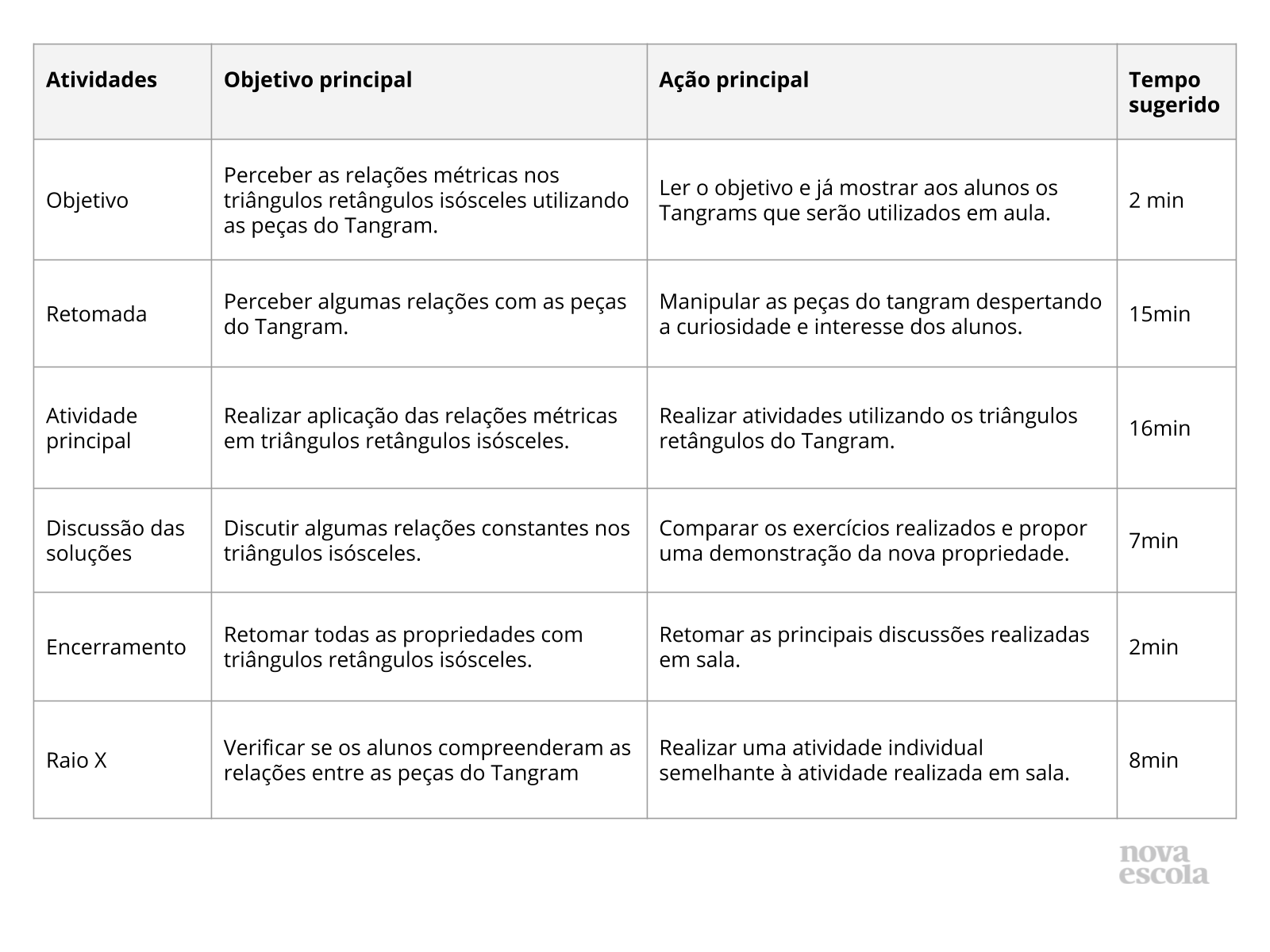 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Durante a explanação do objetivo, separe os alunos em duplas e entregue para cada aluno um jogo de Tangram para que possam já se familiarizar com as peças. Chame a atenção que serão 7 peças: 5 triângulos (dois maiores, dois menores e um de tamanho médio), um quadrado e um paralelogramo. Comente também que os triângulos são todos retângulos e isósceles.
Propósito: Apresentar o objetivo da aula e disponibilizar o Tangram para as duplas.
Discuta com a turma:
- Quais as peças que formam o jogo?
- Há peças iguais? Quais?
- Classifique os triângulos quanto aos lados e aos ângulos.
Retomada

Tempo sugerido: 15 minutos (slides 3 a 6).
Orientações: Entregue as peças do Tangram para cada dupla. O Tangram já deve ter sido produzido. Se sua escola dispõe de jogos de madeira ou EVA, os mesmos podem ser utilizados nas atividades.
Ao entregar os jogos aos alunos incentive-os a conseguir construir um quadrado com as 7 peças. Sempre que usarmos o termo quadrado original estaremos nos remetendo à essa figura formada por todas as peças e formando um quadrado.
Propósito: Desafiar os alunos na montagem de um quadrado utilizando as 7 peças do Tangram. Esse quadrado será sempre utilizado como quadrado inicial.
Discuta com a turma:
- Como você pode encaixar as peças?
- Um quadrado tem quatro ângulos de 90º. Como você pode agrupar essas peças para formar esse ângulo?
- Quais as medidas que se coincidem para poderem se unir? Quais lados são congruentes?
Materiais complementares:
Retomada

Tempo sugerido: 15 minutos (slides 3 a 6).
Orientações: Neste momento vamos comparar apenas os triângulos do Tangram.
São três triângulos diferentes. Não são congruentes, pois não tem lados iguais, mas são semelhantes pois têm ângulos iguais. Para comparar os ângulos podem utilizar o transferidor ou somente sobrepor os ângulos e perceber que podem ser sobrepostos. Então são semelhantes pelo caso AA.
Para perceber os lados coincidentes basta sobrepor as figuras ou alinhá-las lado a lado.
Propósito: Comparar os triângulos do Tangram.
Discuta com a turma:
- O que são figuras congruentes?
- O que são figuras semelhantes?
- Durante a questão f, pergunte aos alunos: qual outra medida conhecida no triângulo além dos lados?
- Todas as alturas estão traçadas?
Retomada

Tempo sugerido: 15 minutos (slides 3 a 6).
Orientações: Os alunos deverão comparar as medidas dos lados das figuras e perceber as que têm mesma medida, relacionando os itens que se destacam. Poderão também comparar medidas que não são iguais, mas são metade ou o dobro.
Propósito: Comparar as peças do Tangram estabelecendo relações entre elas.
Discuta com a turma:
- Quais triângulos têm medidas de lados iguais ao do quadrado? Que lados são esses?
- Quais triângulos têm lados que são o dobro do lado do quadrado? Que lados são esses?
Retomada
Tempo sugerido: 15 minutos (slides 3 a 6).
Orientações: Os alunos deverão comparar as medidas dos lados dos triângulos com os lados do paralelogramo. Como o paralelogramo não tem todos lados iguais, oriente os alunos que compare primeiro o lado menor e depois compare o lado maior para se organizarem melhor.
Propósito: Comparar as peças do Tangram estabelecendo relações entre elas.
Discuta com a turma:
- Analisando o lado menor: quais lados dos triângulos têm a mesma medida deste lado? Quais têm medidas iguais ao dobro? Há mais alguma relação?
- Comparando o lado maior do paralelogramo: quais dos triângulos têm mesma medida deste lado? Quais são maiores que ele? Quais são menores?
Atividade principal

Tempo sugerido: 16 minutos (slides 8 a 11).
Orientações: O aluno trabalhará, neste slide, apenas com o maior triângulo do Tangram. Há dois triângulos maiores, mas iremos trabalhar com apenas um deles. Primeiramente o aluno trabalhará com uma medida de lado qualquer, sempre partindo da medida do lado original do Tangram e a partir daí relacionando as outras medidas da figura. No item c, o aluno será levado a generalizar uma relação entre os catetos e a hipotenusa de um triângulo retângulo isósceles.
Propósito: Perceber as relações métricas no triângulo maior do Tangram.
Discuta com a turma:
- Como posso descobrir a medida da altura? Vamos comparar com o Tangram original para perceber essas relações?
Materiais complementares:
Atividade principal para impressão
Resolução da atividade principal
Guia de intervenção
Materiais Complementares:
Atividade principal

Tempo sugerido: 16 minutos (slides 8 a 11).
Orientações: As relações métricas serão utilizadas para comparar as medidas no triângulo intermediário do Tangram. Dando continuação ao exercício anterior, utilizamos a mesma medida do Tangram anterior para que o aluno dê continuidade ao raciocínio e compare a hipotenusa e sua altura. Neste slide realizaram apenas a medida numérica, mas já é possível comparar algumas medidas (que a altura relativa à hipotenusa é sempre metade da medida da hipotenusa).
Propósito: Perceber as relações métricas no triângulo intermediário do Tangram.
Discuta com a turma:
- Qual a relação dos catetos com a figura inicial?
- Qual a relação da hipotenusa com o triângulo maior? Quais os lados coincidentes?
Atividade principal
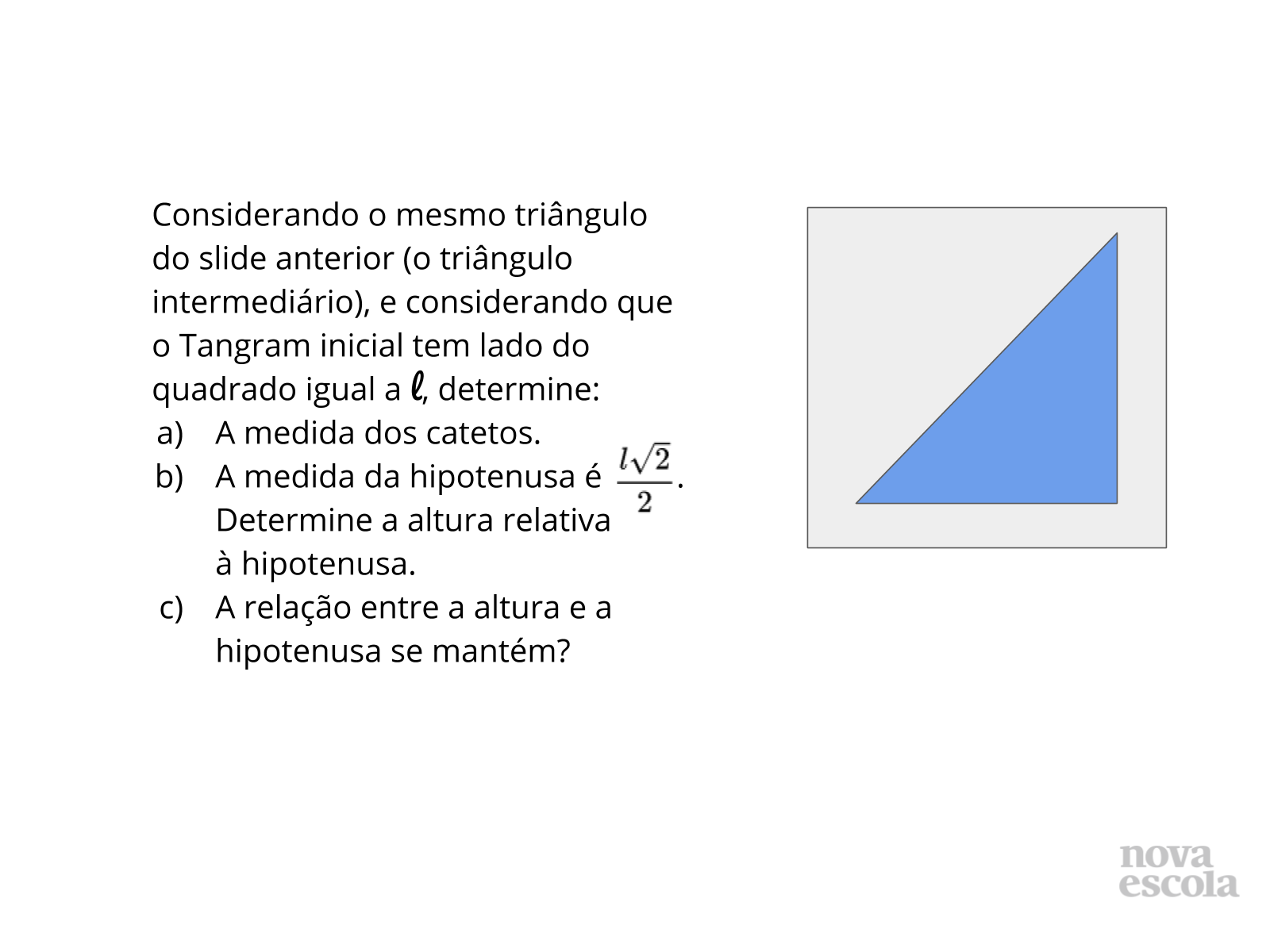
Tempo sugerido: 16 minutos (slides 8 a 11).
Orientações: A comparação neste momento será apenas algébrica, para verificar se as propriedades se mantêm. Os alunos deverão fazer as mesmas conclusões do exercício do slide anterior mas antes foi realizado numericamente e agora será realizado de forma algébrica, generalizando as conclusões anteriores.
Propósito: Perceber as relações métricas no triângulo intermediário do Tangram.
Discuta com a turma:
- Compare as perguntas com a questão anterior. Se o lado do Tangram media 8cm e o cateto 4cm, por ser metade, qual é a metade de l?
- Compare as respostas. Estão de acordo com as perguntas?
Atividade principal

Tempo sugerido: 16 minutos (slides 8 a 11).
Orientações: Vamos comparar o menor triângulo do Tangram. Nos itens a e b os alunos deverão justificar a resposta, pois ela é feita imediatamente da comparação com as figuras anteriores. Apenas o item c é necessário um cálculo. Os alunos podem querer deduzir o valor fazendo a metade da hipotenusa, por dedução dos exercícios anteriores, por isso a exigência do enunciado em aplicar as relações métricas na sua determinação. Somente depois é concluído, novamente, a relação entre essas medidas.
Propósito: Continuar a comparação entre as medidas em triângulos retângulos isósceles.
Discuta com a turma:
- As conclusões que você chegou se aplicaram em todos os triângulos?
Discussão da solução.

Tempo sugerido: 7 minutos (slides 12 a 15).
Orientações: Incentivar os alunos a descobrir se a relação entre a hipotenusa e sua altura em um triângulo retângulo isósceles é sempre válido.
Propósito: Despertar o interesse de provar a nova propriedade utilizando as relações métricas.
Discuta com a turma:
- Essa característica foi válida nos triângulos do Tangram?
- Seriam válidas para todo triângulo retângulo isósceles?
Discussão da solução.
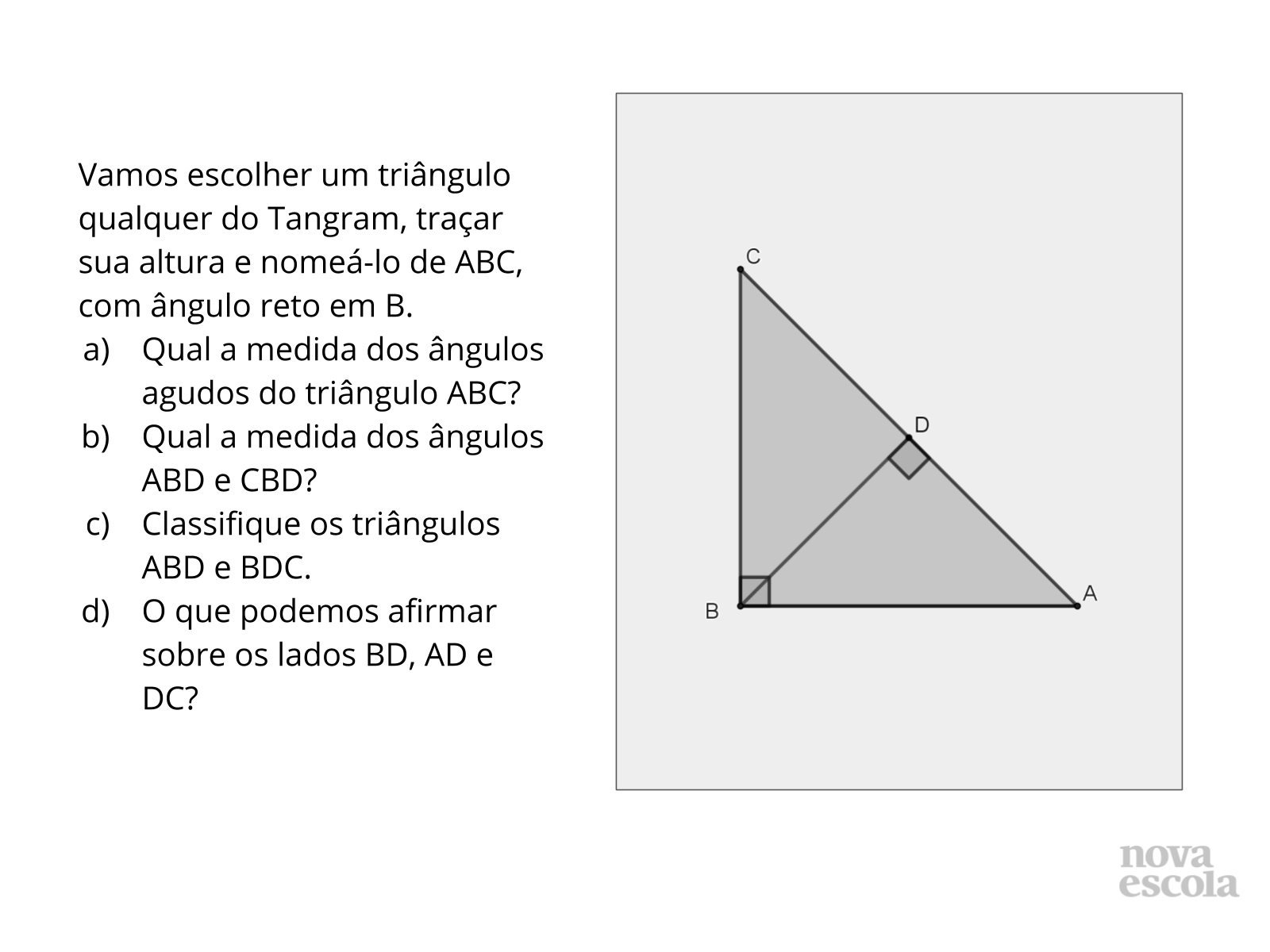
Tempo sugerido: 7 minutos (slides 12 a 15).
Orientações: Utilizando um triângulo retângulo isósceles qualquer o aluno é levado a perceber que ao traçar a altura relativa à hipotenusa é formado um novo triângulo retângulo que também é isósceles. Portanto, os catetos são iguais, ou seja, a altura é igual a metade da hipotenusa.
Propósito: Perceber que a relação entre altura e hipotenusa é válida para todos os triângulos retângulos isósceles.
Discuta com a turma:
- Quais são as características de um triângulo isósceles? O que acontece com seus lados?
- Quais as classificações dos triângulos de acordo com os lados? E de acordo com os ângulos?
Discussão da solução.

Tempo sugerido: 7 minutos (slides 12 a 15).
Orientações: Vamos trabalhar com as outras duas relações métricas utilizando as projeções. Neste momento só vamos relembrar as relações métricas.
Propósito: Retomar as relações métricas que utilizam projeções.
Discuta com a turma:
- Quais as relações métricas que utilizam projeções?
Discussão da solução.
Tempo sugerido: 7minutos (slides 12 a 15).
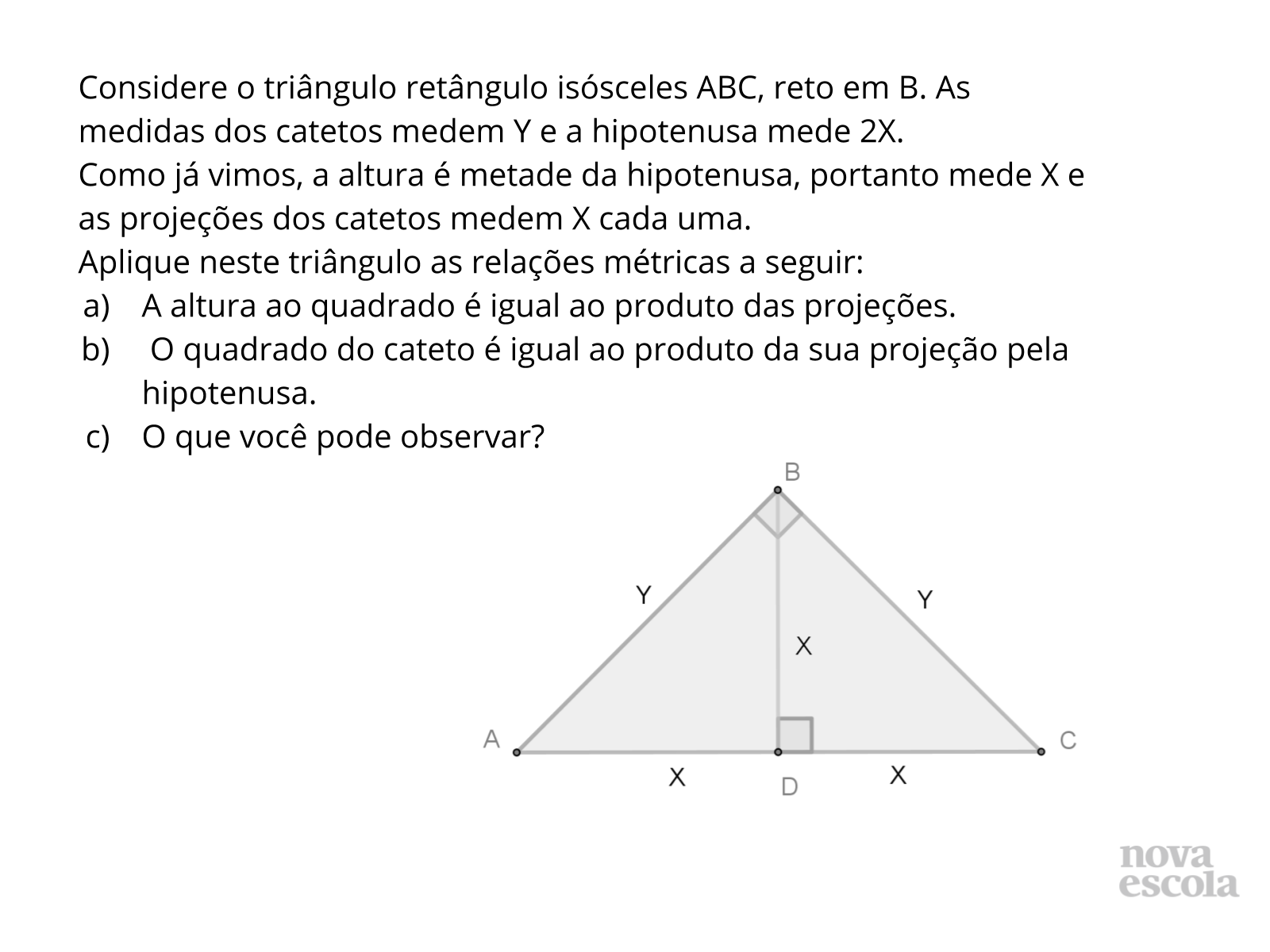
Orientações: Os alunos aplicarão as relações métricas pedidas acima. Antes de partir para o exercício, verifique se todos entenderam porque as medidas são iguais a x e y.
Ao resolver as questões temos:
- X2 = X.X, o que obviamente é verdadeiro.
- Y2 = X.2X ? Y2 = 2.x2 ?Y = x?2.
- Na primeira relação percebemos que é uma igualdade verdadeira e na segunda chegamos à mesma conclusão dos exercícios trabalhados na atividade principal.
Propósito: Perceber que as relações métricas ainda se mantém.
Discuta com a turma:
- Por que os catetos são iguais?
- Por que as projeções são iguais à altura?
Encerramento
Tempo sugerido: 2 minutos.
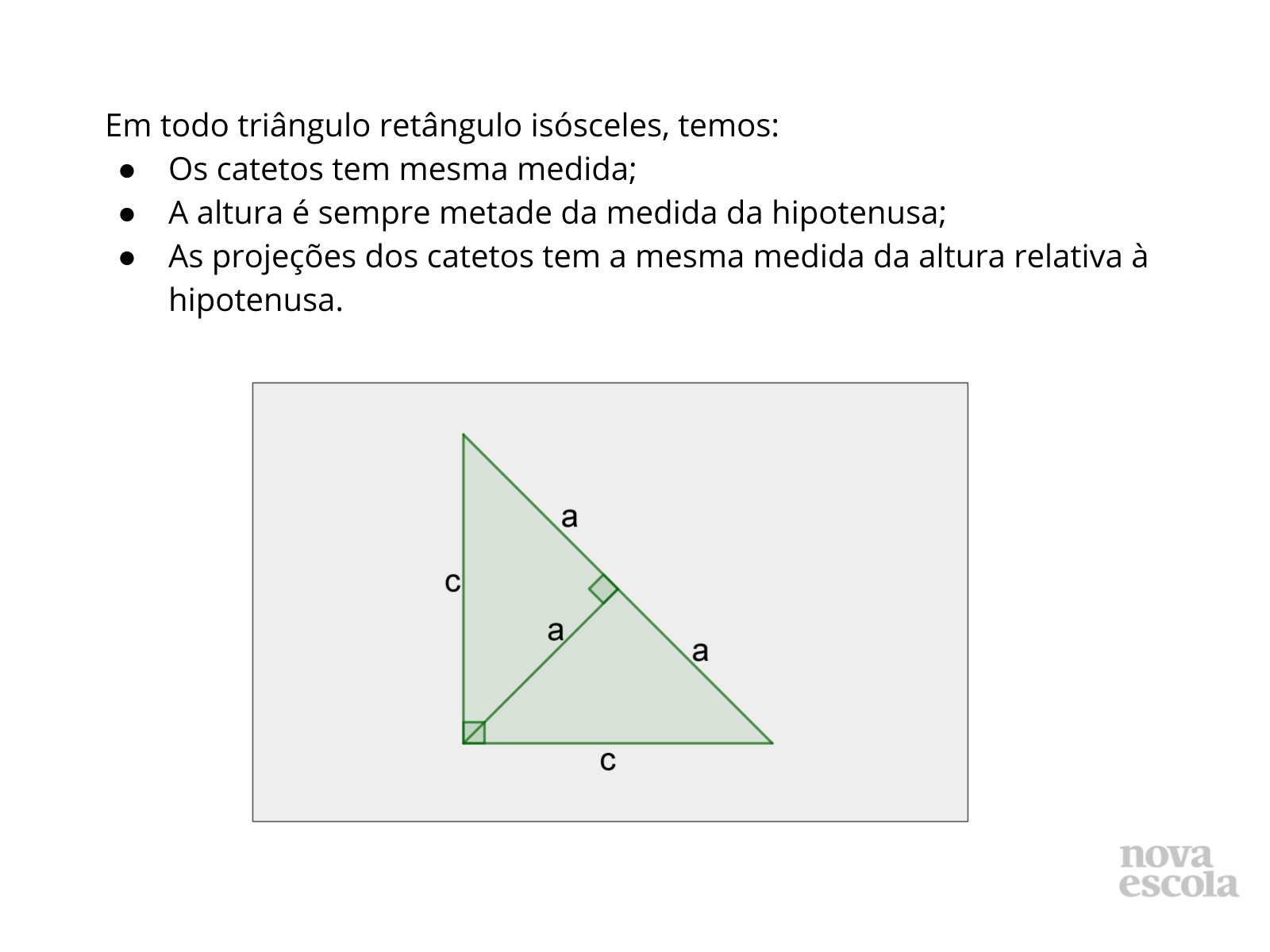
Orientações: Esse slide conclui a aula com as novas observações que as relações métricas trouxeram sobre o triângulo retângulo isósceles. Leia com eles e não esqueça de comentar que todas as relações métricas também continuam válidas.
Propósito: Retomar o que foi observado durante a aula.
Discuta com a turma:
- O que vocês aprenderam hoje?
Raio X
Tempo sugerido: 8 minutos.
Orientações: Neste raio X tentamos explorar as mesmas características realizadas em sala de aula. A atividade será individual.
Propósito: Aplicar as relações métricas em triângulos retângulos, utilizando o Tangram.
Discuta com a turma:
- Houve dificuldade para resolução deste exercício?
Materiais complementares:
Raio X para impressão
Resolução do Raio X
Atividades complementares
Resolução das atividades complementares.
Materiais Complementares:
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_14GEO07)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) e papel para anotações.
- Optativas: Calculadora.
Atividade principal
- Determine que realizem uma pesquisa sobre o TANGRAN, as lendas relacionadas a ele, e construam seus próprios TANGRANs numa folha de papel ou qualquer outro material como EVA.
Discussão das soluções, sistematização e encerramento
- Na discussão das soluções, pergunte sobre as características de cada figura plana do TANGRAN, dando destaque à presença de triângulo retângulos isósceles que têm a altura sendo a metade da hipotenusa, usando as fórmulas das relações métricas.
Raio X
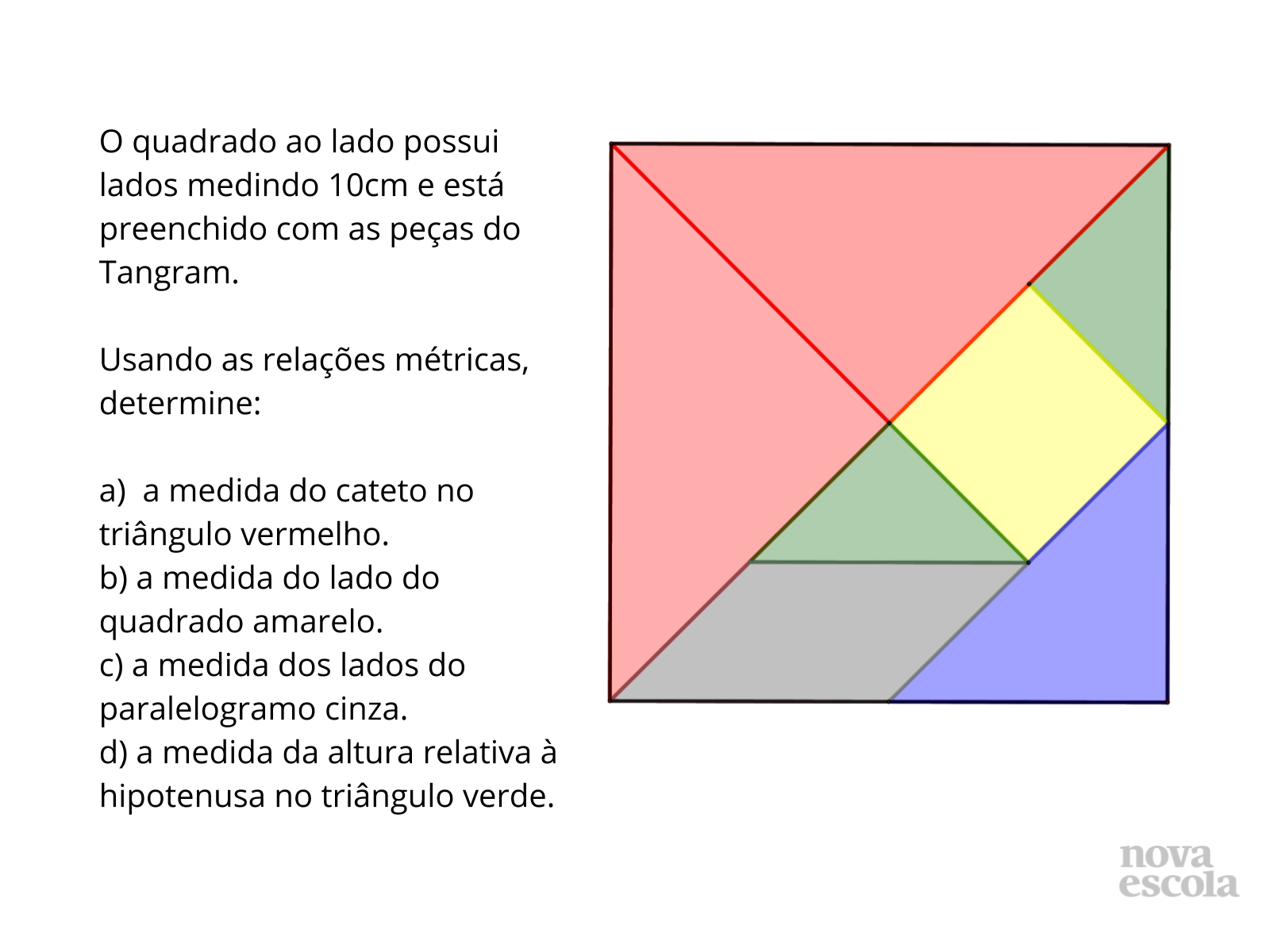
- Determine que construa um TANGRAN específico formando um quadrado com 10 cm. E, usando as relações métricas, determine:
a) a medida do cateto no triângulo vermelho.
b) a medida do lado do quadrado amarelo.
c) a medida dos lados do paralelogramo cinza.
d) a medida da altura relativa à hipotenusa no triângulo verde.
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e relatem suas explorações sobre a pesquisa e curiosidades sobre o TANGRAN.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Flávia Adolf Lutz Keller
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
EF09MA13 - Demonstrar relações métricas do triângulo retângulo.
Objetivos específicos
Utilizar o Tangram para verificar as relações métricas em triângulos retângulos.
Verificar algumas relações específicas em triângulos retângulos isósceles.
Conceito-chave
Relações métricas, triângulo isósceles, tangram.
Recursos necessários
Um tangram por dupla. Se a escola não tiver jogos disponíveis, pode ser colado e recortado em uma cartolina ou papel mais duro (papelão, por exemplo). O modelo para recorte encontra-se no documento ativretom_MAT9_GEO07.














