Resumo da aula
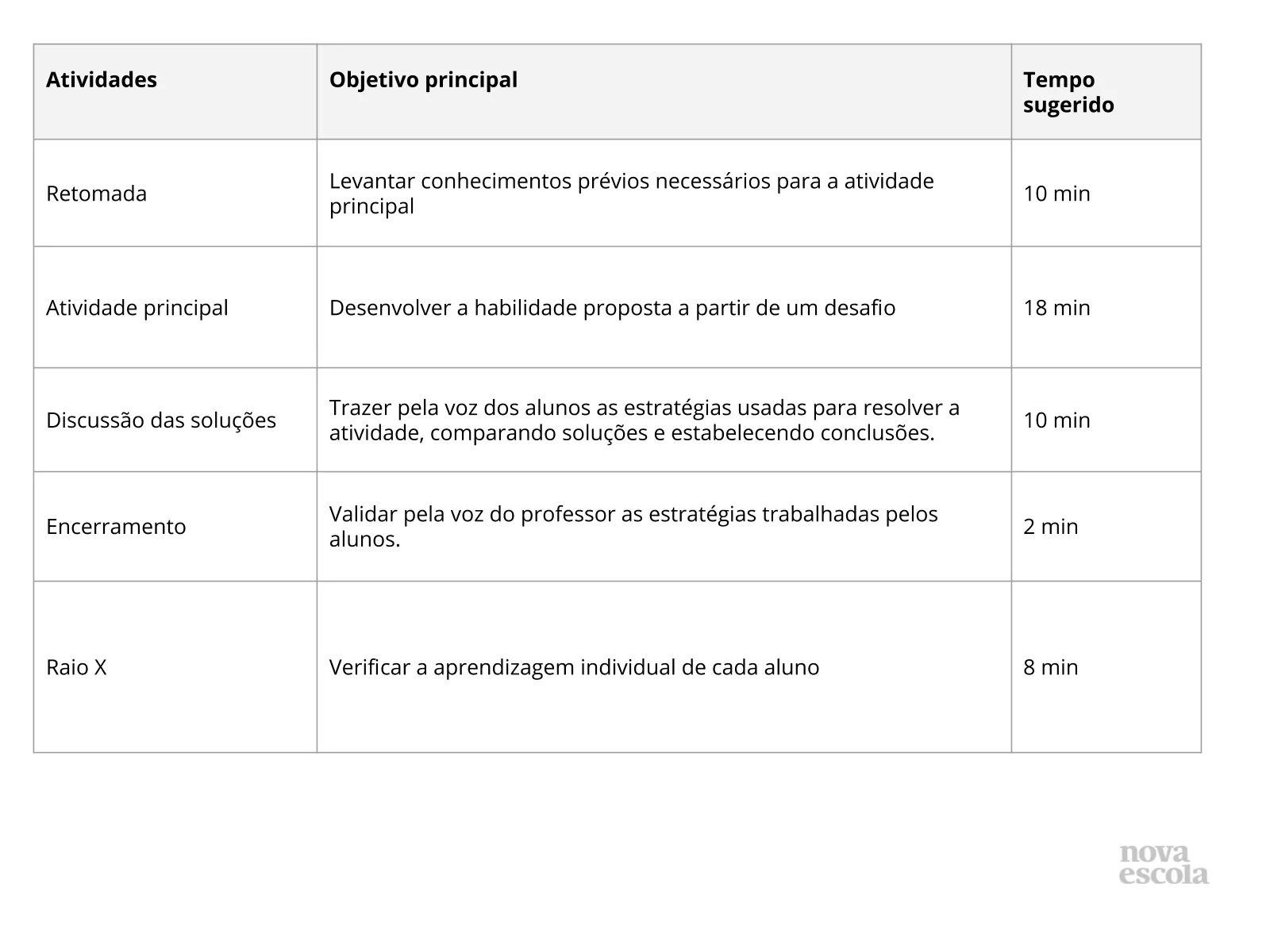
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão. O tempo sugerido prevê 48 minutos de atividade e 2 minutos para compartilhar com a turma o objetivo da aula.
Objetivo

Tempo sugerido: 2 minutos
Orientações:
Compartilhe com a turma o objetivo da aula lendo-o em voz alta, projetando-o (se estiver fazendo uso de apresentação de slides) ou escrevendo-o no quadro.
Atividade principal
Tempo sugerido: 18 minutos (slides 4 e 5)
Orientações:
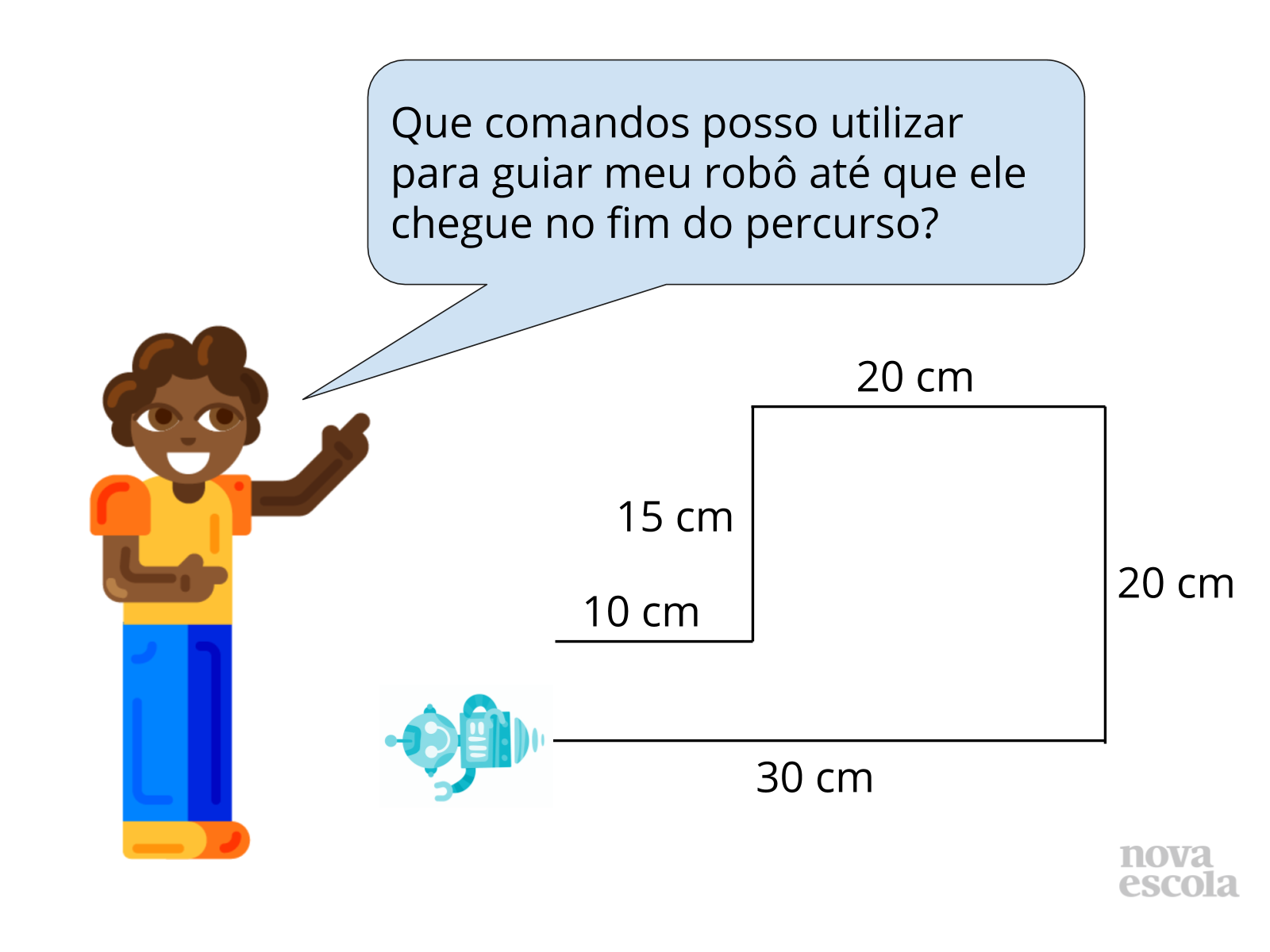
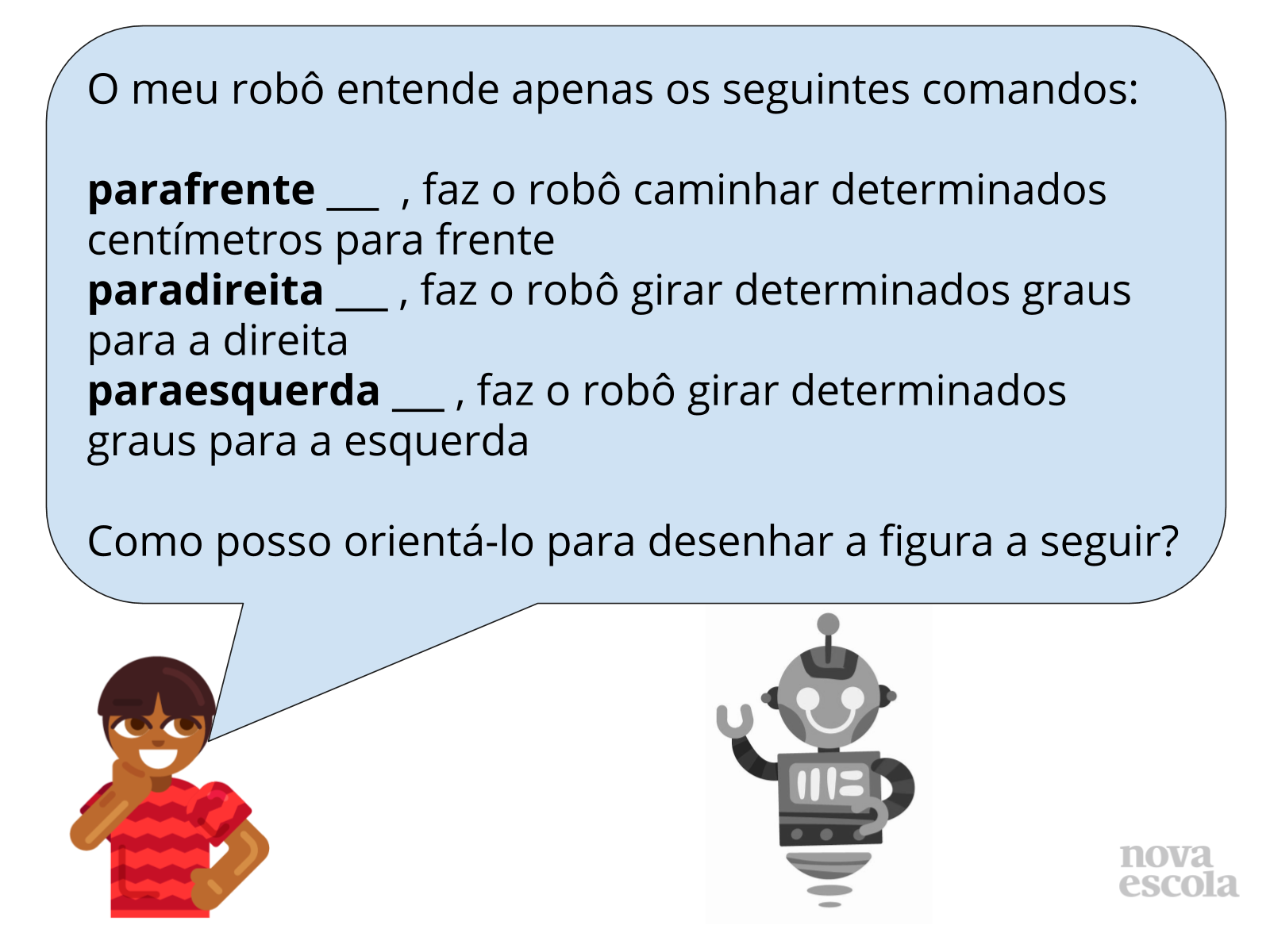
Inicie explicando aos estudantes a linguagem que será utilizada no decorrer desta e das próximas atividades, citando exemplos. Se necessário, peça para que um dos estudantes fique de pé e aproxime-se de você. Solicite para que ele siga os comandos que você falar, como se fosse o robô. Se o piso da sala for de cerâmica, peça para que ele utilize as linhas para se guiar e que cada peça seja encarada como uma unidade de medida. Você pode também pedir para que ele considere os seus passos como unidade de medida.
Após isto, solicite que a turma responda o desafio em seu caderno.
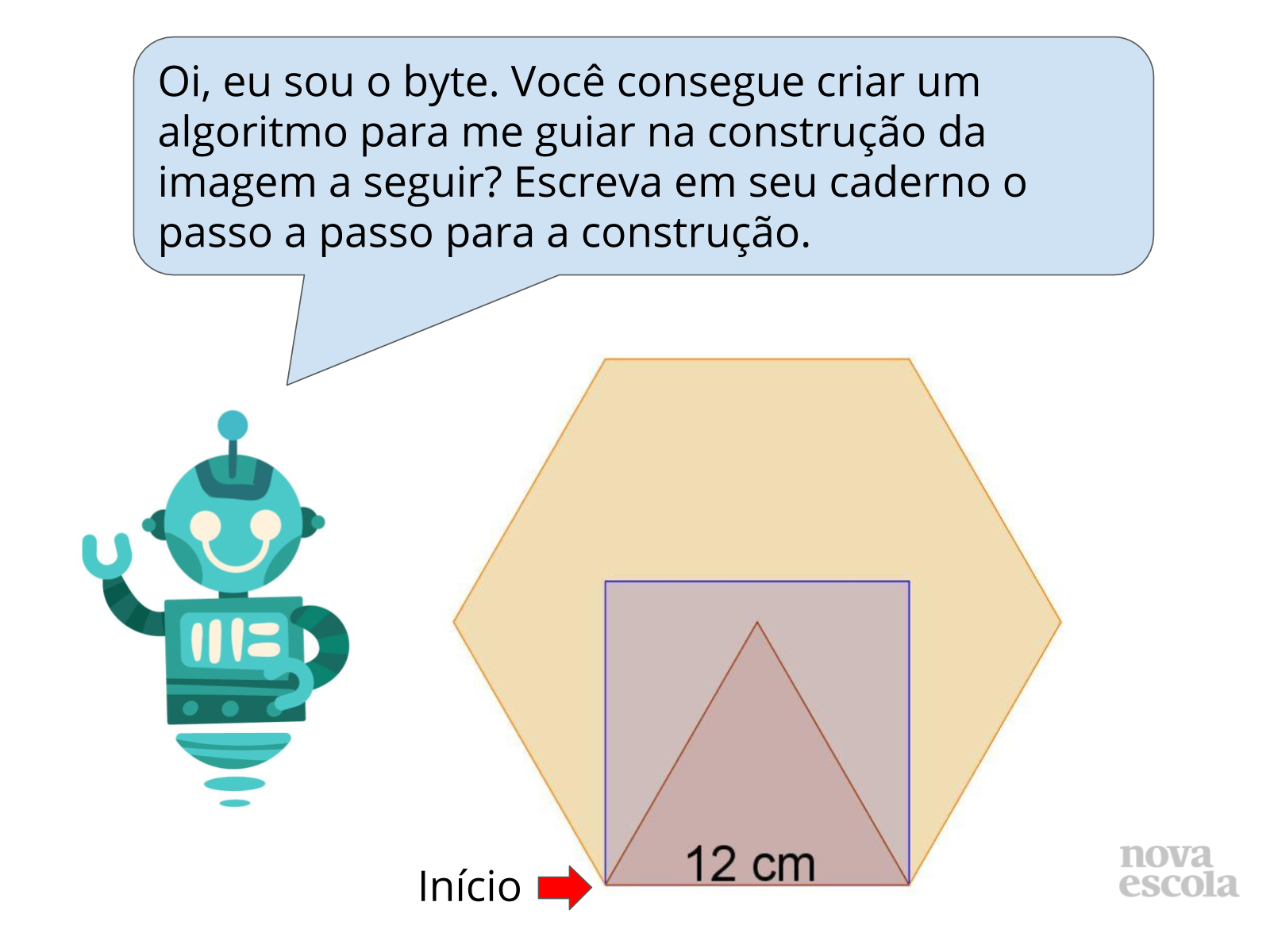
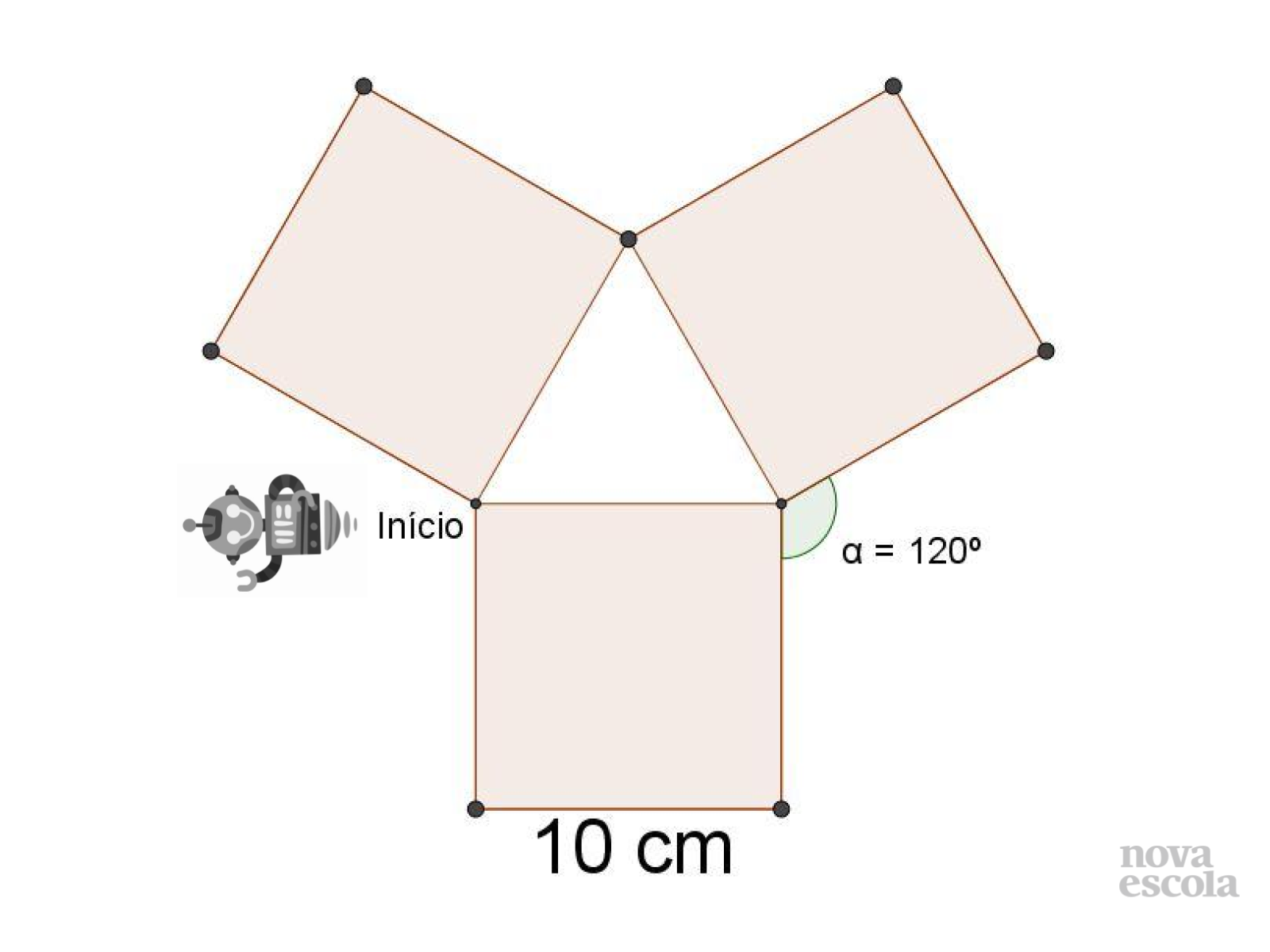
Sugira que os estudantes utilizem o transferidor para medir os ângulos não indicados, especialmente os formados entre os quadrados. Sugira que utilizem também o compasso e régua para verificar as medidas não indicadas.
Enquanto os estudantes respondem, circule pela sala e verifique se existem dúvidas sobre o funcionamento do algoritmo combinado.
Caso algum estudante possuam dificuldades em iniciar a atividade, faça-lhe algumas perguntas que o leve a refletir sobre o objetivo da aula e resgatar alguns conhecimentos prévios, como:
- Por onde o robô deverá iniciar?
- Em qual direção ele se moverá? Até aonde?
- Em seguida, o que ele deverá fazer? Como podemos dizer isto utilizando uma linguagem que ele consiga entender?
- Quais ângulos nesta atividade são iguais? E quais são diferentes?
Propósito:
Trabalhar com os estudantes a utilização de algoritmos que descrevam a construção de formas geométricas utilizando alguma linguagem de códigos específica.
Materiais complementares:
Atividade Principal para impressão: https://nova-escola-producao.s3.amazonaws.com/YxfgrGQVp9TNEsARjDHgYxdBmc5ABrSjBaUJdWDpBEmNFGTVv57yyQbjCwar/atividade-principal-mat6-27geo03.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/VUHAkM8Y4FTUScxT32udp44cNdSHMqj6TWts34UAYyYqXUM6EUSrTxZm54Ss/resolucao-das-atividades-mat6-27geo03.pdf
Materiais de apoio:
Consulte um material sobre a linguagem Super Logo, elaborado por Viviane MarcelIa dos Santos da Universidade Estadual Paulista no ano de 2006: <http://wwwp.fc.unesp.br/~mauri/Logo/Superlogo.pdf>.
Atividade principal
Tempo sugerido: 18 minutos (slides 4 e 5)
Orientações:
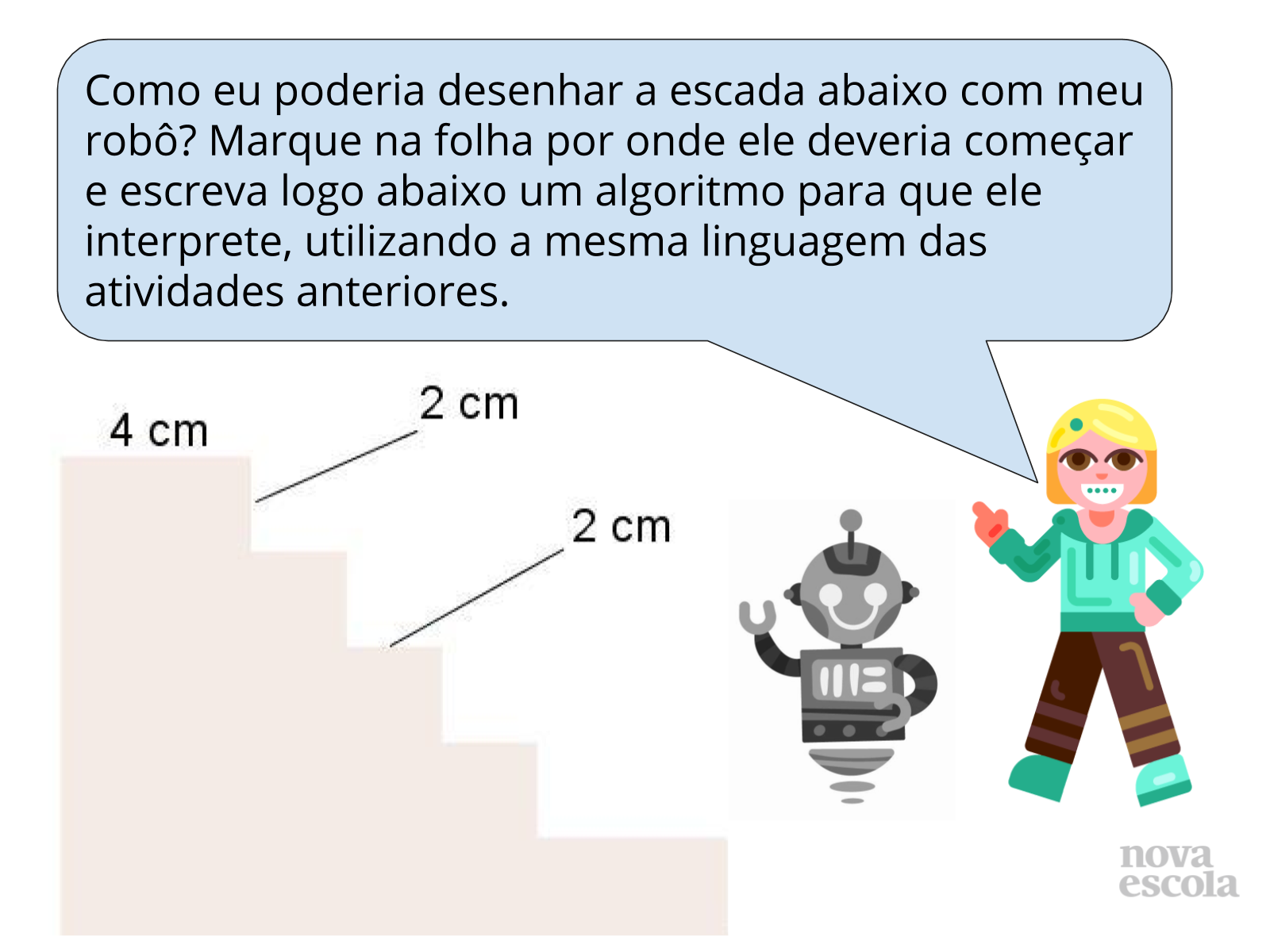
Inicie explicando aos estudantes a linguagem que será utilizada no decorrer desta e das próximas atividades, citando exemplos. Se necessário, peça para que um dos estudantes fique de pé e aproxime-se de você. Solicite para que ele siga os comandos que você falar, como se fosse o robô. Se o piso da sala for de cerâmica, peça para que ele utilize as linhas para se guiar e que cada peça seja encarada como uma unidade de medida. Você pode também pedir para que ele considere os seus passos como unidade de medida.
Após isto, solicite que a turma responda o desafio em seu caderno.
Sugira que os estudantes utilizem o transferidor para medir os ângulos não indicados, especialmente os formados entre os quadrados. Sugira que utilizem também o compasso e régua para verificar as medidas não indicadas.
Enquanto os estudantes respondem, circule pela sala e verifique se existem dúvidas sobre o funcionamento do algoritmo combinado.
Caso algum estudante possuam dificuldades em iniciar a atividade, faça-lhe algumas perguntas que o leve a refletir sobre o objetivo da aula e resgatar alguns conhecimentos prévios, como:
- Por onde o robô deverá iniciar?
- Em qual direção ele se moverá? Até aonde?
- Em seguida, o que ele deverá fazer? Como podemos dizer isto utilizando uma linguagem que ele consiga entender?
- Quais ângulos nesta atividade são iguais? E quais são diferentes?
Propósito:
Trabalhar com os estudantes a utilização de algoritmos que descrevam a construção de formas geométricas utilizando alguma linguagem de códigos específica.
Discussão das soluções

Tempo sugerido: 10 minutos
Orientações:
Inicie solicitando que os estudantes compartilhem algumas de suas respostas, para que verifiquem os caminhos que trilharam e se levam à construção da figura solicitada.
Você pode pedir, inclusive, para que os estudantes troquem suas respostas tentando executar os comandos dos colegas.
Caso também hajam erros entre as respostas apresentadas, levante questionamentos para a turma, para que encontrem e reflitam como eles poderiam ser corrigidos, como:
- Há algum passo neste algoritmo que atrapalha a construção das figuras? Qual?
- É possível apenas apagar este passo, mantendo a coerência na construção das figuras? Se não, como esse passo poderia ser construído?
Em seguida, apresente a resolução do slide 5 e discuta com a turma sobre como a personagem poderia continuar ou modificar o seu algoritmo.
Propósito:
Socializar e discutir as diferentes resoluções propostas pelos alunos.
Discuta com a turma:
- Quais foram os diferentes algoritmos criados? Todos levaram à construção da figura?
- É possível simplificar esses algoritmos? De que forma?
Materiais complementares:
Guia de intervenção: https://nova-escola-producao.s3.amazonaws.com/QVTBbyERQgYg3zJqDuFTDswcs7YtYsvbhNMq6c7ATXYnA229ECRramUunwwp/guia-de-intervencao-mat6-27geo03.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/VUHAkM8Y4FTUScxT32udp44cNdSHMqj6TWts34UAYyYqXUM6EUSrTxZm54Ss/resolucao-das-atividades-mat6-27geo03.pdf
Encerramento
Tempo sugerido: 2 minutos
Orientações:
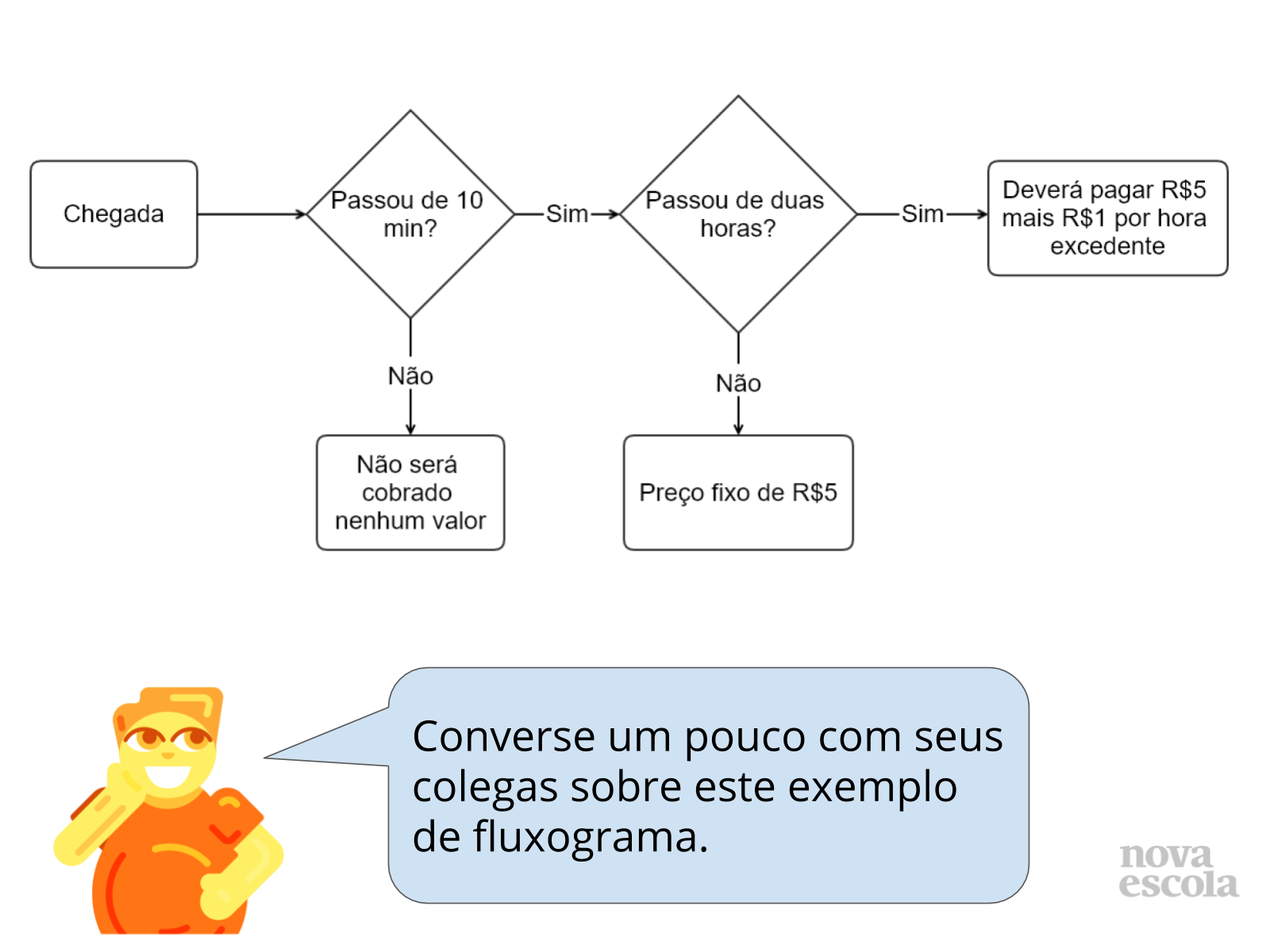
Peça para que um dos alunos leia em voz alta a fala da robô no slide.
Peça também para que alguns alunos falem o que mais gostaram na aula e o que aprenderam de novo.
Propósito:
Retomar as principais aprendizagens da aula.