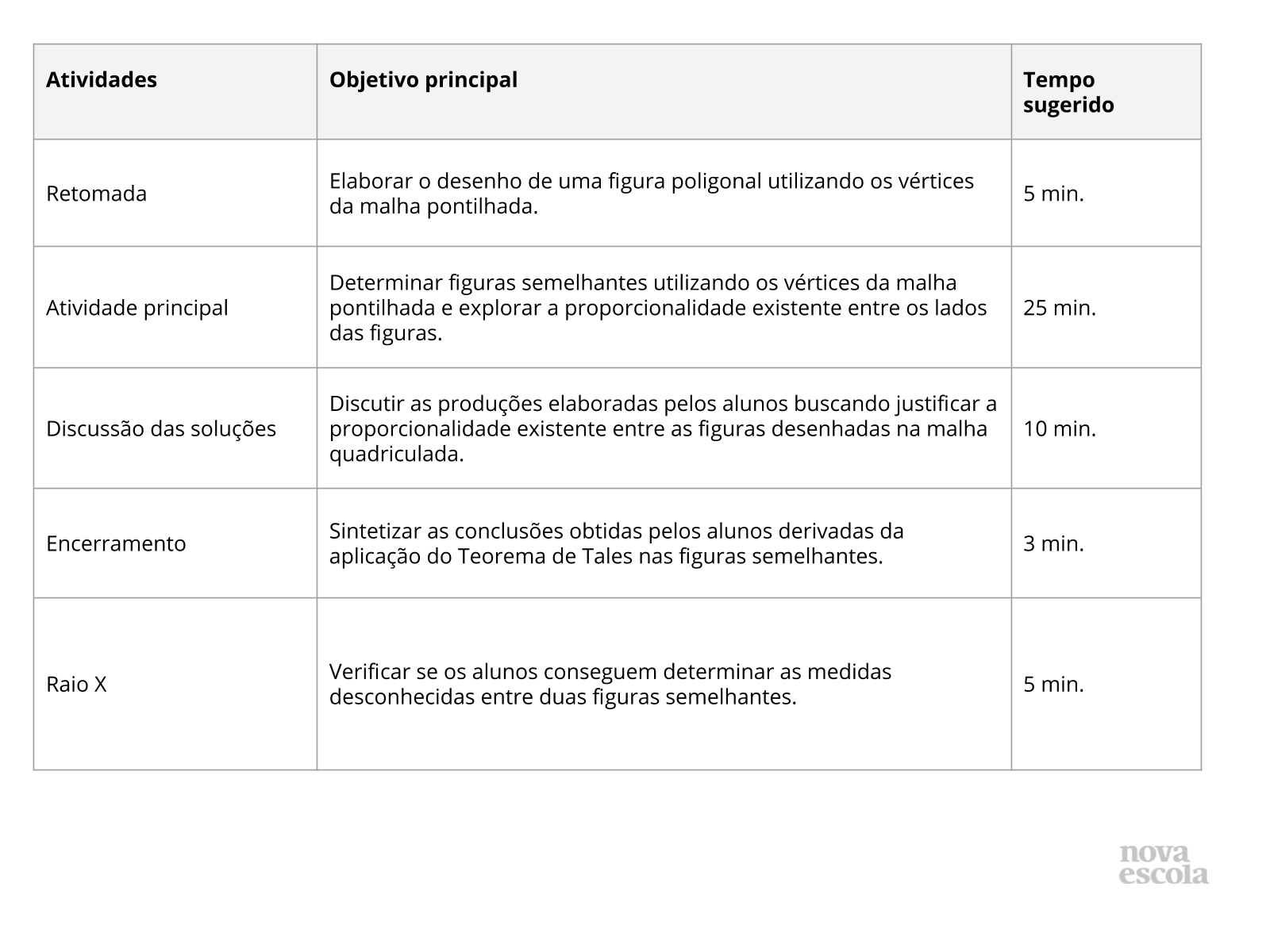
Atividade Retomada
Plano de Aula
Plano de aula: Ampliando figuras e descobrindo relações
Plano 11 de uma sequência de 11 planos. Veja todos os planos sobre Teorema de Pitágoras e suas aplicações
Descrição
Habilidade da BNCC
(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
Objetivos específicos
- Desenhar figuras utilizando os pontos da malha quadriculada;
- Explorar a proporcionalidade existente entre os lados de figuras semelhantes;
- Justificar a proporcionalidade apresentada em figuras semelhantes utilizando o Teorema de Tales.
Habilidades BNCC:
Objetivos de aprendizagem
- Desenhar figuras utilizando os pontos da malha quadriculada;
- Explorar a proporcionalidade existente entre os lados de figuras semelhantes;
- Justificar a proporcionalidade apresentada em figuras semelhantes utilizando o Teorema de Tales.
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão. O tempo sugerido prevê 48 minutos de atividade e 2 minutos para compartilhar com a turma o objetivo da aula.
Objetivo

Tempo sugerido: 2 minutos
Orientações:
Compartilhe com a turma o objetivo da aula lendo-o em voz alta, projetando-o (se estiver fazendo uso de apresentação de slides) ou escrevendo-o no quadro.
Retomada
Tempo sugerido: 5 minutos
Orientações:
Antes da aula iniciar organize as carteiras em U pois desta maneira você terá fácil acesso às produções dos alunos. Além disso caso algum aluno apresente alguma dificuldade você poderá intervir de forma mais ágil. Inicie a aula projetando a pergunta ou lendo para a turma o questionamento. Entregue uma malha quadriculada para cada aluno e dê alguns minutos para os alunos elaborarem suas produções. Enquanto os alunos desenham percorra as carteiras verificando se os alunos estão utilizando os vértices da própria malha quadriculada como vértices das figuras. Esta etapa da aula condiz com a familiarização e na correta elaboração da figura para a Atividade Principal.
Propósito:
Elaborar uma figura usando os vértices da malha quadriculada.
Discuta com a turma:
- Você utilizou os vértices da malha quadriculada para formar sua figura?
- Tem algum vértice da figura que não coincide com vértices da malha quadriculada?
- Todos os vértices foram ligados para compor sua figura?
Materiais complementares:
Atividade Retomada: https://nova-escola-producao.s3.amazonaws.com/sm6Bm5MyeavbeJCwu2Wbd7GCs2W9GCJMQX87kPDazwjgtAJYNYgqUwZrX6Jr/atividade-retomada-mat9-15geo11.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/Ur6t2mUzpjKtwNATNvHcNY8wJE9VS5cdMEeSVsmBXEG265XvHgPcJaWXh4Bs/resolucao-das-atividades-mat9-15geo11.pdf
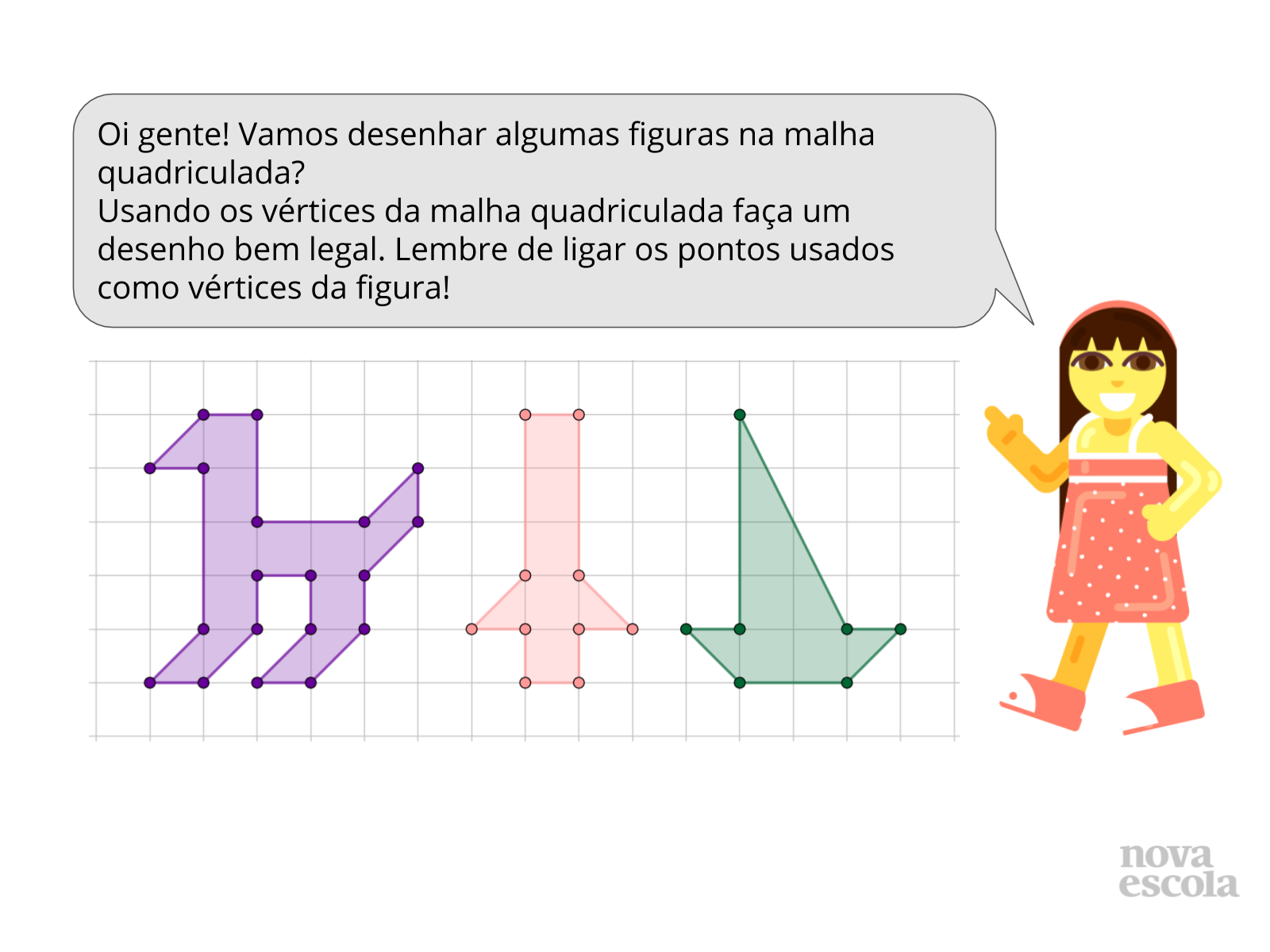
Atividade principal
Tempo sugerido: 25 minutos (slides 4, 5 e 6)
Orientações:
Peça para os alunos escolherem um vértice da malha quadriculada que esteja na região externa da figura elaborada. A partir deste vértice solicite que os alunos tracem retas o ligando a cada vértice da figura desenhada.
Num segundo momento os alunos deverão determinar os pontos de intersecção entre as retas traçadas e os vértices da malha quadriculada. O objetivo é traçar uma figura semelhante à figura inicial. Caso algum aluno apresente dificuldade nesta etapa peça para ele observar os quadradinhos da malha quadriculada para identificar os demais vértices a partir de um ponto previamente determinado. Determinado os pontos os alunos deverão ligá-los para obter a figura ampliada/reduzida.
Distribua réguas e transferidores para os alunos e faça a leitura das questões do slide 6. Verifique entre os alunos compreenderam todos os questionamentos ou se desconhecem alguma palavra/conceito. Dê alguns minutos para que os alunos responderem as perguntas e discutirem entre si aquelas que forem necessárias. Aproveite este momento para selecionar algumas produções dos alunos (corretas ou não) para discussão da próxima etapa.
Propósito:
Determinar uma figura semelhante a original utilizando os vértices da malha quadriculada.
Discuta com a turma:
- Você traçou todas as retas a partir do ponto exterior? Faltou alguma reta ligando algum vértice.
- Os vértices da segunda figura coincidem com os vértices da malha quadriculada?
- Existe algum termo (do slide 6) que você desconhece?
Materiais complementares:
Atividade Principal para impressão: https://nova-escola-producao.s3.amazonaws.com/fveHknzRreQW8xMqduwTVecc5WtCR4vSmAJVMfw5VNuemBVE4t6kQyqK5RzD/atividade-principal-mat9-15geo11.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/Ur6t2mUzpjKtwNATNvHcNY8wJE9VS5cdMEeSVsmBXEG265XvHgPcJaWXh4Bs/resolucao-das-atividades-mat9-15geo11.pdf
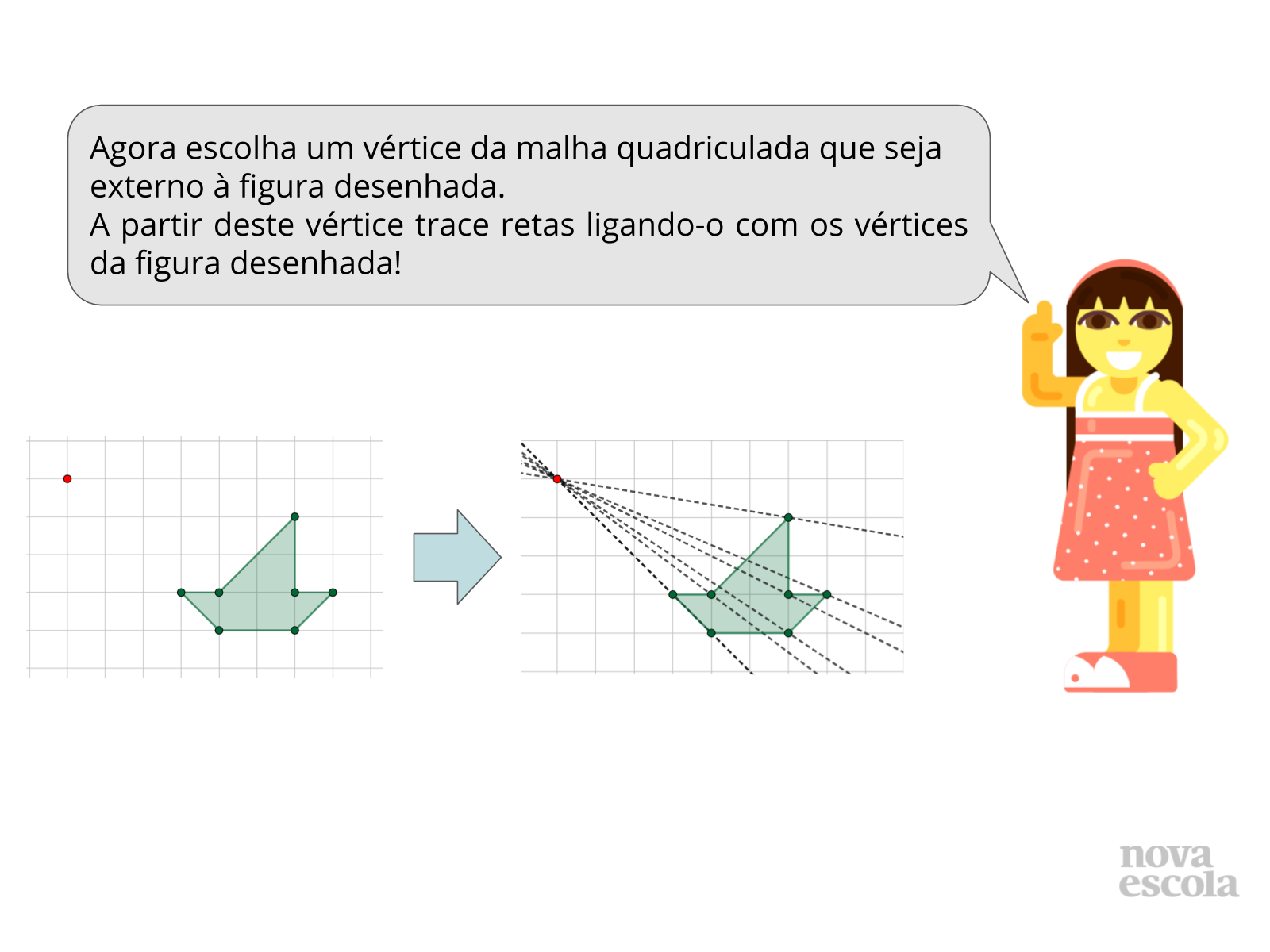
Atividade principal
Tempo sugerido: 25 minutos (slides 4, 5 e 6)
Orientações:
Peça para os alunos escolherem um vértice da malha quadriculada que esteja na região externa da figura elaborada. A partir deste vértice solicite que os alunos tracem retas o ligando a cada vértice da figura desenhada.
Num segundo momento os alunos deverão determinar os pontos de intersecção entre as retas traçadas e os vértices da malha quadriculada. O objetivo é traçar uma figura semelhante à figura inicial. Caso algum aluno apresente dificuldade nesta etapa peça para ele observar os quadradinhos da malha quadriculada para identificar os demais vértices a partir de um ponto previamente determinado. Determinado os pontos os alunos deverão ligá-los para obter a figura ampliada/reduzida.
Distribua réguas e transferidores para os alunos e faça a leitura das questões do slide 6. Verifique entre os alunos compreenderam todos os questionamentos ou se desconhecem alguma palavra/conceito. Dê alguns minutos para que os alunos responderem as perguntas e discutirem entre si aquelas que forem necessárias. Aproveite este momento para selecionar algumas produções dos alunos (corretas ou não) para discussão da próxima etapa.
Propósito:
Determinar uma figura semelhante a original utilizando os vértices da malha quadriculada.
Discuta com a turma:
- Você traçou todas as retas a partir do ponto exterior? Faltou alguma reta ligando algum vértice.
- Os vértices da segunda figura coincidem com os vértices da malha quadriculada?
- Existe algum termo (do slide 6) que você desconhece?
Materiais complementares:
Atividade Principal para impressão:
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/Ur6t2mUzpjKtwNATNvHcNY8wJE9VS5cdMEeSVsmBXEG265XvHgPcJaWXh4Bs/resolucao-das-atividades-mat9-15geo11.pdf
Atividade principal

Tempo sugerido: 25 minutos (slides 4, 5 e 6)
Orientações:
Peça para os alunos escolherem um vértice da malha quadriculada que esteja na região externa da figura elaborada. A partir deste vértice solicite que os alunos tracem retas o ligando a cada vértice da figura desenhada.
Num segundo momento os alunos deverão determinar os pontos de intersecção entre as retas traçadas e os vértices da malha quadriculada. O objetivo é traçar uma figura semelhante à figura inicial. Caso algum aluno apresente dificuldade nesta etapa peça para ele observar os quadradinhos da malha quadriculada para identificar os demais vértices a partir de um ponto previamente determinado. Determinado os pontos os alunos deverão ligá-los para obter a figura ampliada/reduzida.
Distribua réguas e transferidores para os alunos e faça a leitura das questões do slide 6. Verifique entre os alunos compreenderam todos os questionamentos ou se desconhecem alguma palavra/conceito. Dê alguns minutos para que os alunos responderem as perguntas e discutirem entre si aquelas que forem necessárias. Aproveite este momento para selecionar algumas produções dos alunos (corretas ou não) para discussão da próxima etapa.
Propósito:
Determinar uma figura semelhante a original utilizando os vértices da malha quadriculada.
Discuta com a turma:
- Você traçou todas as retas a partir do ponto exterior? Faltou alguma reta ligando algum vértice.
- Os vértices da segunda figura coincidem com os vértices da malha quadriculada?
- Existe algum termo (do slide 6) que você desconhece?
Materiais complementares:
Atividade Principal para impressão: https://nova-escola-producao.s3.amazonaws.com/fveHknzRreQW8xMqduwTVecc5WtCR4vSmAJVMfw5VNuemBVE4t6kQyqK5RzD/atividade-principal-mat9-15geo11.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/Ur6t2mUzpjKtwNATNvHcNY8wJE9VS5cdMEeSVsmBXEG265XvHgPcJaWXh4Bs/resolucao-das-atividades-mat9-15geo11.pdf
Discussão das soluções
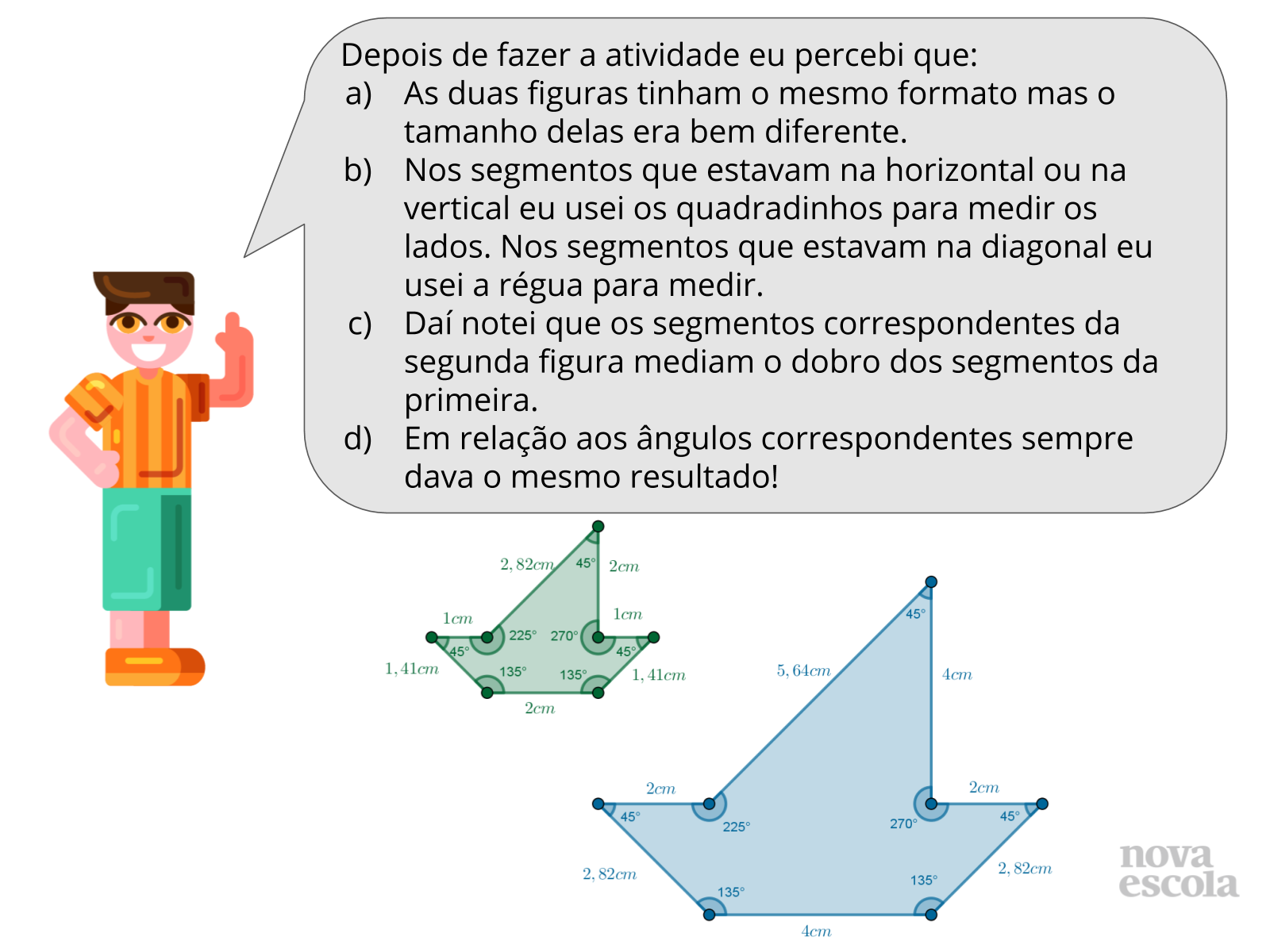
Tempo sugerido: 10 minutos (slides 7 e 8)
Orientações:
Selecione algumas produções elaboradas e peça para que os alunos expliquem como responderam os questionamentos do slide 6. Inicie a discussão apontando as semelhanças e diferenças entre as figuras inicial e final obtidas. O objetivo é levar o aluno a perceber que apesar de ambas figuras apresentarem o mesmo formato, seus lados são proporcionais.
Outro ponto importante é levar o aluno a concluir que como os lados da segunda figura são proporcionais, seu perímetro também será.
Por último os alunos deverão justificar o por quê as figuras são proporcionais. Caso os alunos mostrem dificuldade nesta etapa peça para que os alunos tracem retas paralelas usando os vértices das figuras. Depois pergunte sobre as retas que interceptam o feixe de retas paralelas (retas transversais). Por último solicite que os alunos destaquem os segmentos determinados que coincidem com os lados das figuras desenhadas.
Propósito:
Comunicar e discutir os resultados obtidos na exploração anterior envolvendo os segmentos determinados pelas transversais no feixe de paralelas.
Discuta com a turma:
- Você notou algo entre as figuras desenhadas? Me explique com suas palavras as características das figuras desenhadas.
- Depois que realizou as medidas dos lados e dos ângulos o quê você pode afirmar sobre ambas figuras?
- Por quê você acha que isto ocorre com os lados dessas figuras? Como as retas traçadas interceptam as figuras desenhadas.
Materiais complementares:
Guia de intervenção: https://nova-escola-producao.s3.amazonaws.com/nndNeWaHRqesKZazgjN8fJQDMBD797JWmhKvDvXqwcVsPdHwZJKeTnkRMAux/guia-de-intervencoes-mat9-15geo11.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/Ur6t2mUzpjKtwNATNvHcNY8wJE9VS5cdMEeSVsmBXEG265XvHgPcJaWXh4Bs/resolucao-das-atividades-mat9-15geo11.pdf
Discussão das soluções
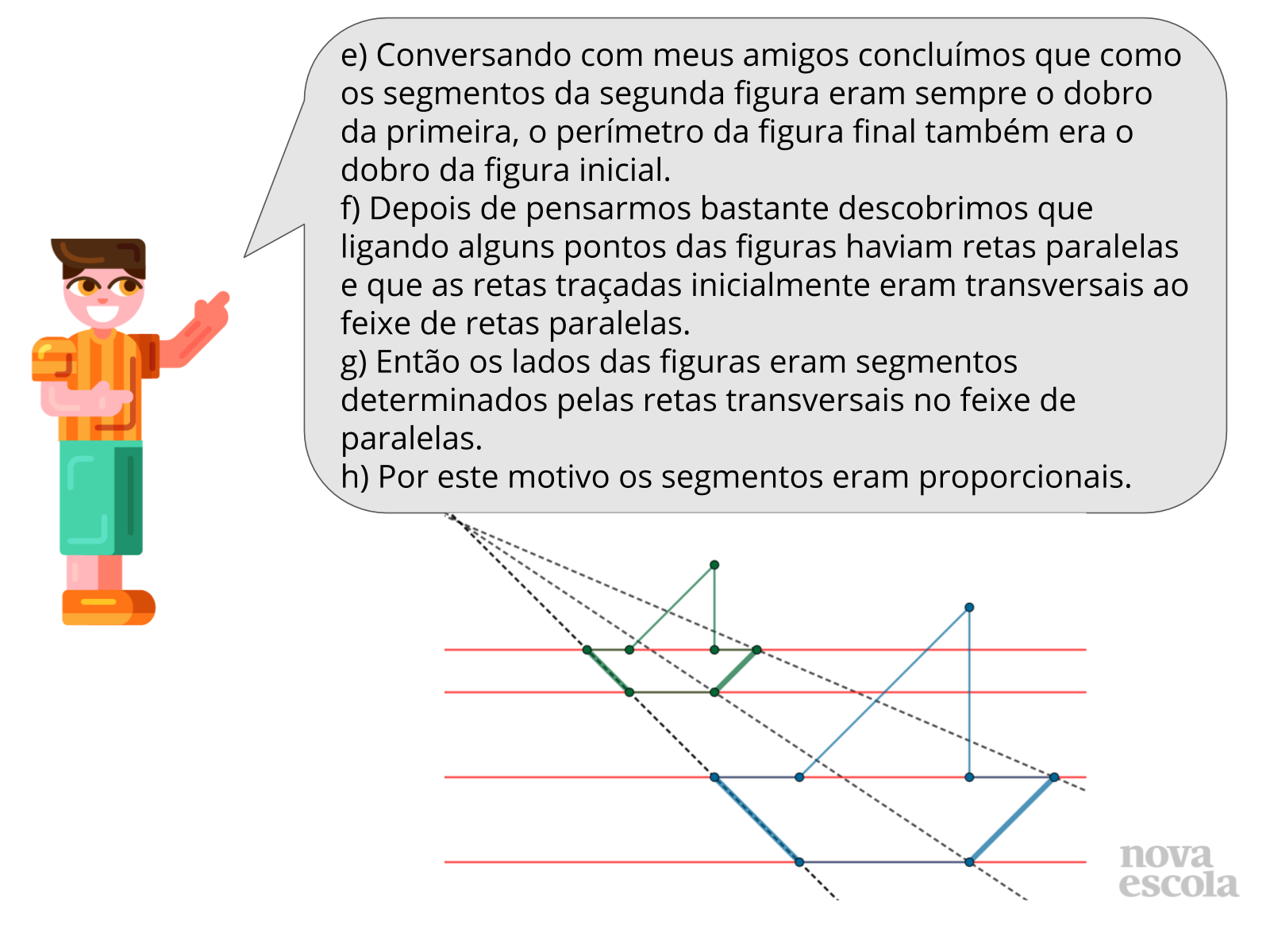
Tempo sugerido: 10 minutos (slides 7 e 8)
Orientações:
Selecione algumas produções elaboradas e peça para que os alunos expliquem como responderam os questionamentos do slide 6. Inicie a discussão apontando as semelhanças e diferenças entre as figuras inicial e final obtidas. O objetivo é levar o aluno a perceber que apesar de ambas figuras apresentarem o mesmo formato, seus lados são proporcionais.
Outro ponto importante é levar o aluno a concluir que como os lados da segunda figura são proporcionais, seu perímetro também será.
Por último os alunos deverão justificar o por quê as figuras são proporcionais. Caso os alunos mostrem dificuldade nesta etapa peça para que os alunos tracem retas paralelas usando os vértices das figuras. Depois pergunte sobre as retas que interceptam o feixe de retas paralelas (retas transversais). Por último solicite que os alunos destaquem os segmentos determinados que coincidem com os lados das figuras desenhadas.
Propósito:
Comunicar e discutir os resultados obtidos na exploração anterior envolvendo os segmentos determinados pelas transversais no feixe de paralelas.
Discuta com a turma:
- Você notou algo entre as figuras desenhadas? Me explique com suas palavras as características das figuras desenhadas.
- Depois que realizou as medidas dos lados e dos ângulos o quê você pode afirmar sobre ambas figuras?
- Por quê você acha que isto ocorre com os lados dessas figuras? Como as retas traçadas interceptam as figuras desenhadas.
Materiais complementares:
Guia de intervenção: https://nova-escola-producao.s3.amazonaws.com/nndNeWaHRqesKZazgjN8fJQDMBD797JWmhKvDvXqwcVsPdHwZJKeTnkRMAux/guia-de-intervencoes-mat9-15geo11.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/Ur6t2mUzpjKtwNATNvHcNY8wJE9VS5cdMEeSVsmBXEG265XvHgPcJaWXh4Bs/resolucao-das-atividades-mat9-15geo11.pdf
Encerramento

Tempo sugerido: 3 minutos
Orientações:
Peça para que um aluno faça a leitura das instruções presentes no slide e questione a turma sobre as condições necessárias para que haja a ampliação/redução das figuras.
Propósito:
Refletir sobre o objetivo da aula e verificar quanto é possível utilizar o resultado desenvolvido.
Discuta com a turma:
Como devemos fazer para saber a medida do lado de uma figura sabendo a medida do lado correspondente?
Raio X
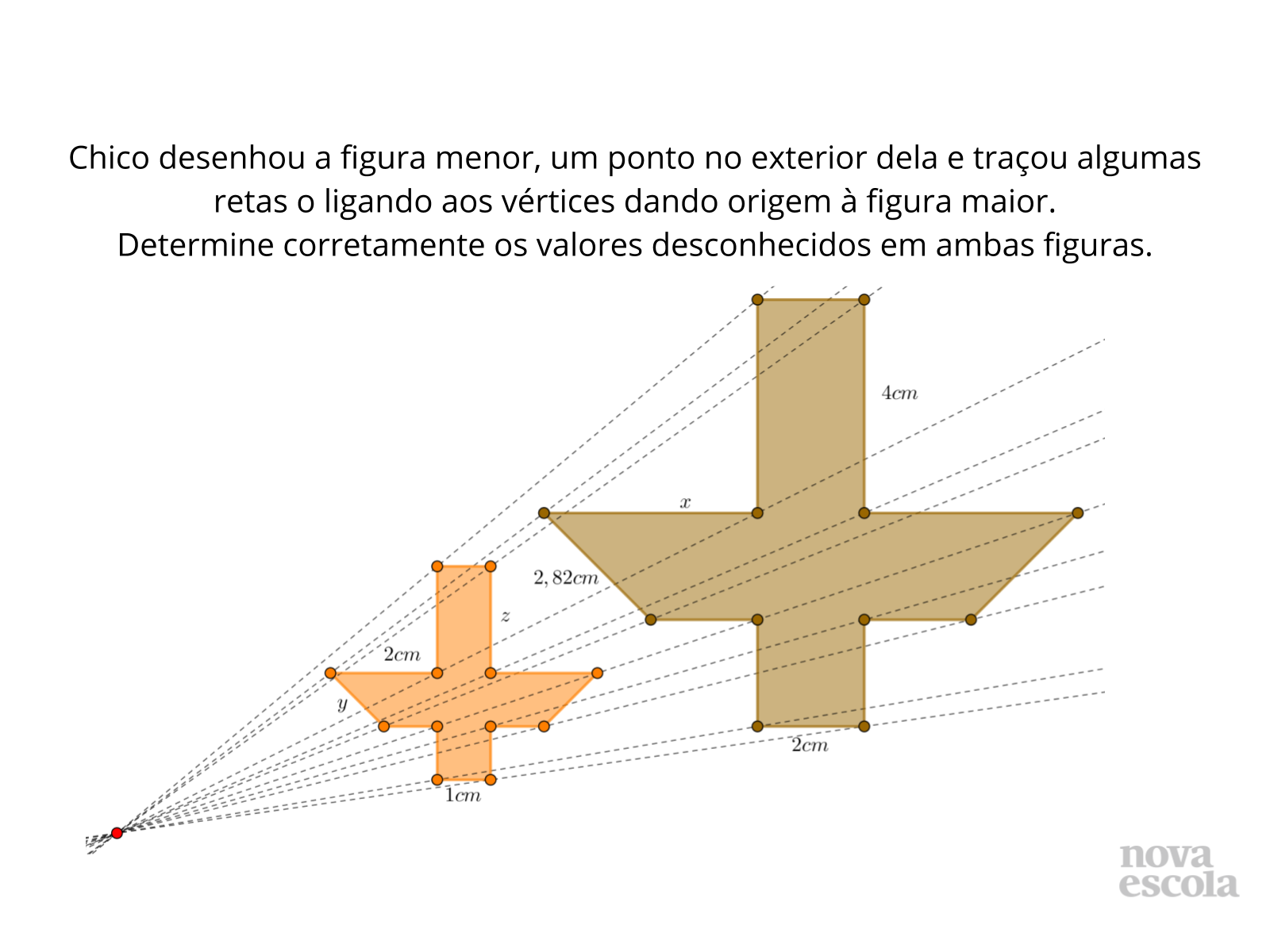
Tempo sugerido: 5 minutos
Orientações:
Entregue para cada aluno uma cópia da atividade e solicite que leiam atentamente o enunciado. Pergunte se há alguma dúvida em relação ao comando da atividade e a esclareça se houver necessidade. Recolha as atividades e verifique se os alunos desenvolveram adequadamente o objetivo da aula (explorar a proporcionalidade envolvendo os lados de figuras semelhantes).
Propósito:
Verificar se os alunos desenvolveram adequadamente o objetivo da aula.
Discuta com a turma:
- Mostre os lados correspondentes entre ambas figuras? Você percebeu algo entre algum par de lados correspondentes?
- A partir da conclusão observada anteriormente como você acha que seriam as medidas dos demais lados das figuras?
Materiais complementares:
Atividade Raio X: https://nova-escola-producao.s3.amazonaws.com/DGqHMgDvJYYytys4ZRjf4WGNdJADf7prEtgp2JeqkpHmPnDmdGNMQM9Z3S42/atividade-raio-x-mat9-15geo11.pdf
Atividades Complementares: https://nova-escola-producao.s3.amazonaws.com/qgjYF9KSBTSkAZbbPZTcP8XKHZ7arTyDb55nQBJM9EnpX8RJv4dzdtJfmeC8/atividades-complementares-mat9-15geo11.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/Ur6t2mUzpjKtwNATNvHcNY8wJE9VS5cdMEeSVsmBXEG265XvHgPcJaWXh4Bs/resolucao-das-atividades-mat9-15geo11.pdf
Para o aluno
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_15GEO11)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) e papel para anotações.
- Optativas: Calculadora.
Atividade principal
- Pela rede social escolhida, para essa atividade principal, disponibilize o papel quadriculado na unidade escolar ou um PDF para impressão.
- Aplique a atividade passo a passo para posterior discussão das soluções.
Discussão das soluções
- Na discussão das soluções, a grande preocupação deve ser relacionar a semelhança entre as figuras e a proporcionalidade entre os lados das figuras criadas.
Sistematização e encerramento
- Na sistematização e encerramento deve-se reforçar que é uma situação derivada da aplicação do teorema de Tales e por isso existe a proporcionalidade.
- Sem esquecer de dizer que essa aplicação foi feita por um processo chamado homotetia.
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, no auxílio aos desenhos criados e discussões sobre a semelhança.
Habilidade da BNCC
(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
Objetivos específicos
- Desenhar figuras utilizando os pontos da malha quadriculada;
- Explorar a proporcionalidade existente entre os lados de figuras semelhantes;
- Justificar a proporcionalidade apresentada em figuras semelhantes utilizando o Teorema de Tales.















