Resumo da aula
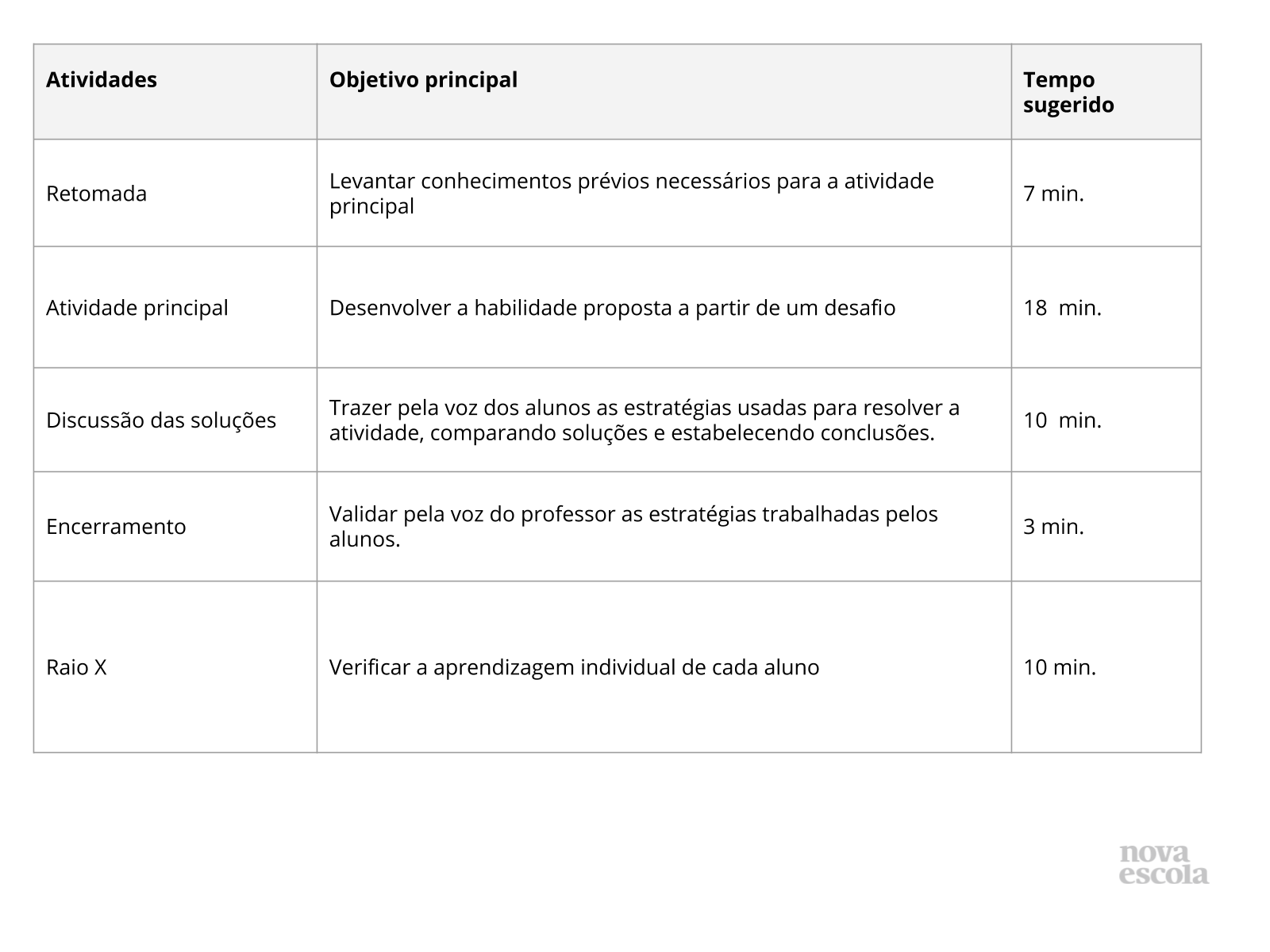
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão. O tempo sugerido prevê 48 minutos de atividade e 2 minutos para compartilhar com a turma o objetivo da aula.
Objetivo

Tempo sugerido: 2 minutos
Orientações:
Compartilhe com a turma o objetivo da aula lendo-o em voz alta, projetando-o (se estiver fazendo uso de apresentação de slides) ou escrevendo-o no quadro.
Atividade principal

Tempo sugerido: 18 minutos (slides 4 e 5)
Orientações:
Leia o texto inicial sobre figuras fractais. Se preferir, aprofunde o conteúdo mostrando outros exemplos. Apresente em seguida a sequência de triângulos Sierpinski, formado por triângulos equiláteros pretos. Explore essa representação, fazendo alguns questionamentos do item discuta com a turma.
Propósito:
Identificar uma sequência presente nos triângulos, representando os termos dessa sequência, de forma numérica e algébrica.
Discuta com a turma:
- Esses triângulos formam uma sequência?
- É possível explicar verbalmente como acontece a regularidade dessa sequência?
- Você consegue determinar o próximo termo da sequência?
- Quantos outros termos (triângulos) você conseguiria desenhar?
Discussão das soluções

Tempo sugerido: 10 minutos (Slides 6 e 7)
Orientações:
Pergunte aos alunos sobre as estratégias que utilizaram para resolver os questionamentos. Monte um painel de soluções das respostas realizadas nas duplas e ouça as diferentes e possíveis formas de pensar dos alunos e deixe que eles apresentem seus argumentos para defender suas soluções, privilegiando acertos e erros, e fazendo intervenções quando necessário. O guia de intervenções poderá lhe ajudar nesse momento.
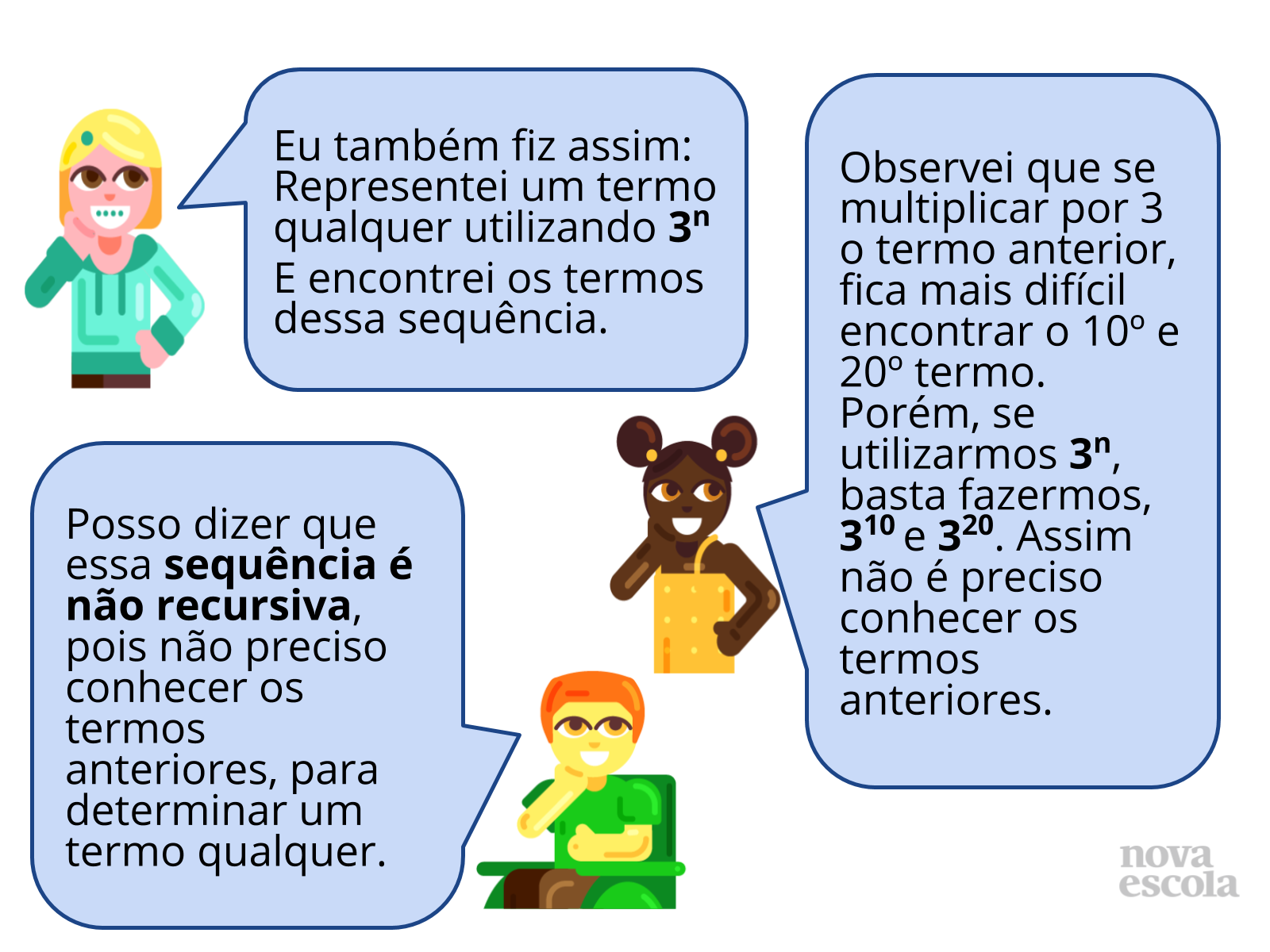
Em seguida, apresente as possíveis soluções dos slides em forma de diálogo, destacando nesse momento a identificação, organização, regularidade, termo qualquer na sua continuidade, representação numérica e algébrica presentes nesta sequência, destacando a diferença entre sequência recursiva e não recursiva, e mostrando que uma sequência pode ser ao mesmo tempo recursiva e não recursiva.
Exemplo: Na sequência da atividade se multiplicarmos termo anterior por 3 é recursiva, mas se considerarmos 3 elevado ao número da posição na sequência é não recursiva.
Propósito:
Discutir as possíveis soluções, fazendo um fechamento das ideias discutidas até o momento.
Materiais complementares:
Guia de intervenções: https://nova-escola-producao.s3.amazonaws.com/qCcSyJNNsUzgYPtAR95B5m6GrqUxT68uDFbp82Q2K2JSGnZ3PsQrGNVdWtJ6/guia-de-intervencao-mat7-10alg07.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/MHWCnmPsx7hYbHh4Mawx56V36eGdapMTCBkrHNDANdmWDSTmncyKYaexV5dd/resolucoes-de-atividades-mat7-10alg07.pdf
Discussão das soluções
Tempo sugerido: 10 minutos (Slides 6 e 7)
Orientações:
Pergunte aos alunos sobre as estratégias que utilizaram para resolver os questionamentos. Monte um painel de soluções das respostas realizadas nas duplas e ouça as diferentes e possíveis formas de pensar dos alunos e deixe que eles apresentem seus argumentos para defender suas soluções, privilegiando acertos e erros, e fazendo intervenções quando necessário. O guia de intervenções poderá lhe ajudar nesse momento.
Em seguida, apresente as possíveis soluções dos slides em forma de diálogo, destacando nesse momento a identificação, organização, regularidade, termo qualquer na sua continuidade, representação numérica e algébrica presentes nesta sequência, destacando a diferença entre sequência recursiva e não recursiva, e mostrando que uma sequência pode ser ao mesmo tempo recursiva e não recursiva.
Exemplo: Na sequência da atividade se multiplicarmos termo anterior por 3 é recursiva, mas se considerarmos 3 elevado ao número da posição na sequência é não recursiva.
Propósito:
Discutir as possíveis soluções, fazendo um fechamento das ideias discutidas até o momento.
Encerramento

Tempo sugerido: 3 minutos
Orientações:
Leia ou projete o texto para os alunos, reforçando de forma clara e objetiva o conceito trabalhado na aula. Explique para seus alunos que uma sequência pode ser ao mesmo tempo recursiva e não recursiva, relembre o que são figuras fractais.
Propósito:
Encerrar a aula resumindo o que foi estudado sobre sequências.
Materiais complementares:
Veja esse artigo sobre Fractais no link: https://www.infoescola.com/matematica/geometria-fractal/
Raio X
Tempo sugerido: 10 minutos (Slides 9 e 10)
Orientações:
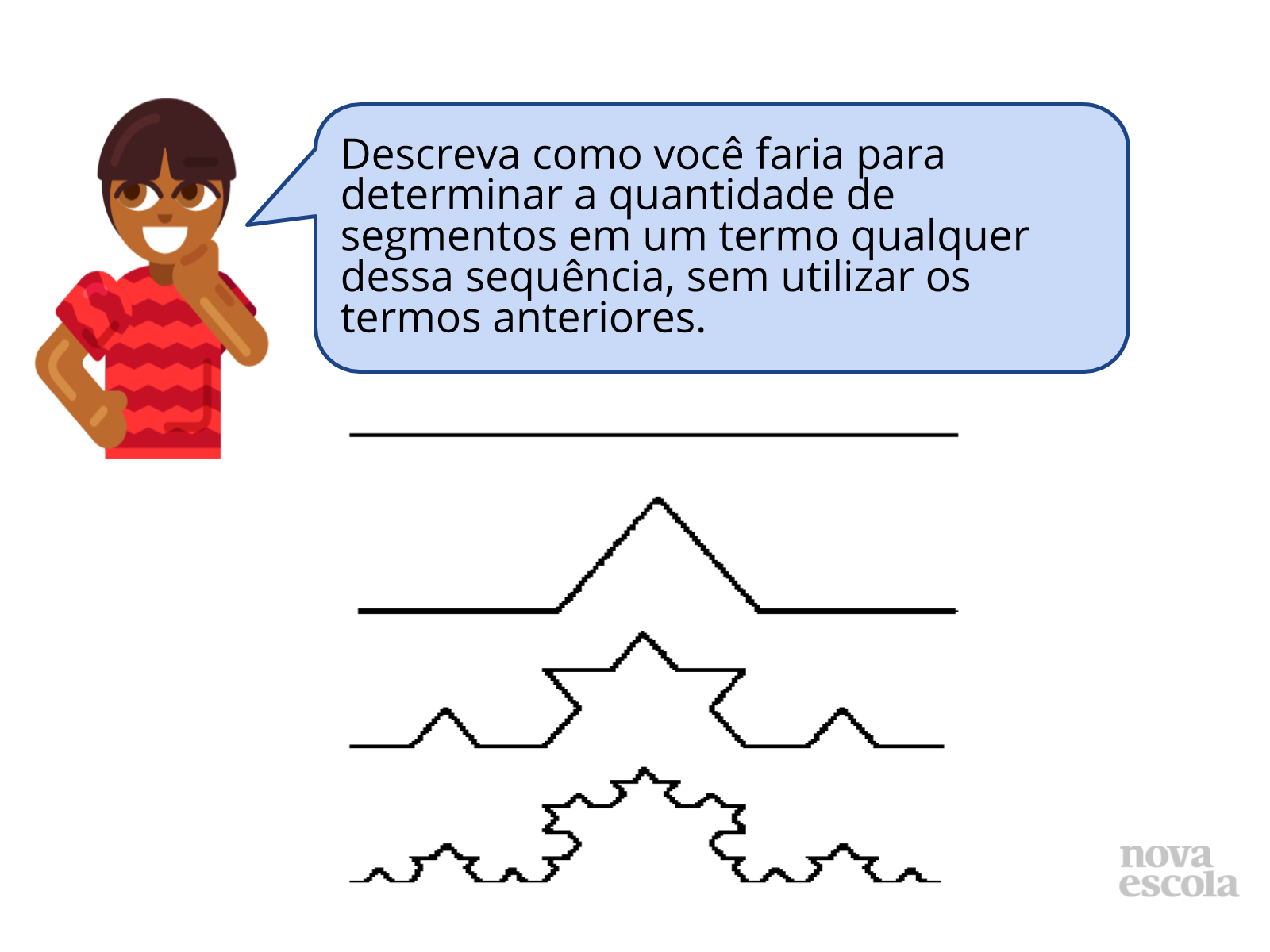
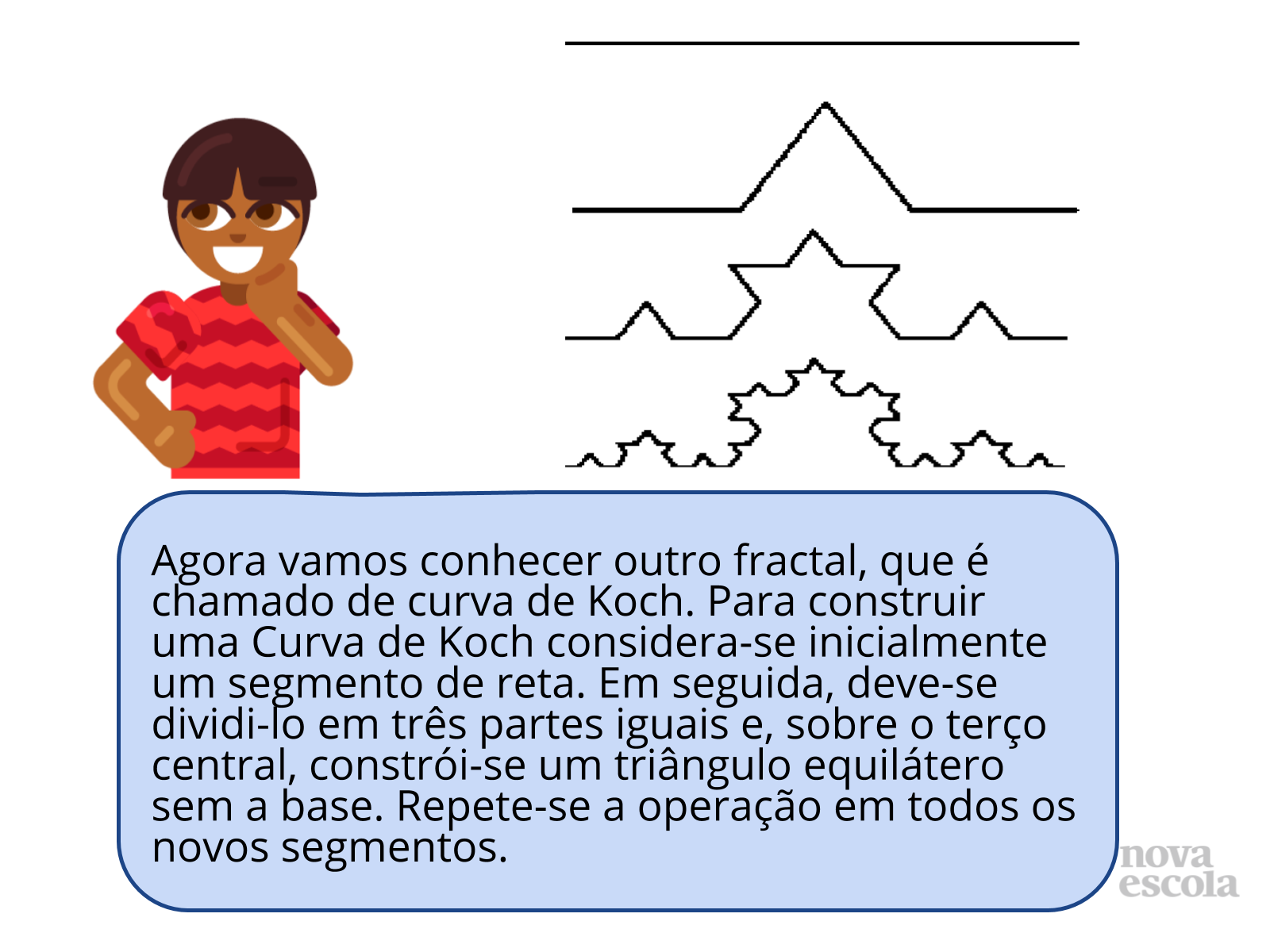
Leia o texto inicial sobre um fractal chamado de curva de Koch. Apresente em seguida a sequência da curva de Koch, formado por segmentos de reta. Explore essa representação, fazendo alguns questionamentos do item discuta com a turma.
Propósito:
Representar os seus termos da sequência numericamente e simbolicamente.
Discuta com a turma:
- Qual o termo seguinte na continuidade dessa sequência?
- Quantos termos você consegue representar?