Resumo da aula
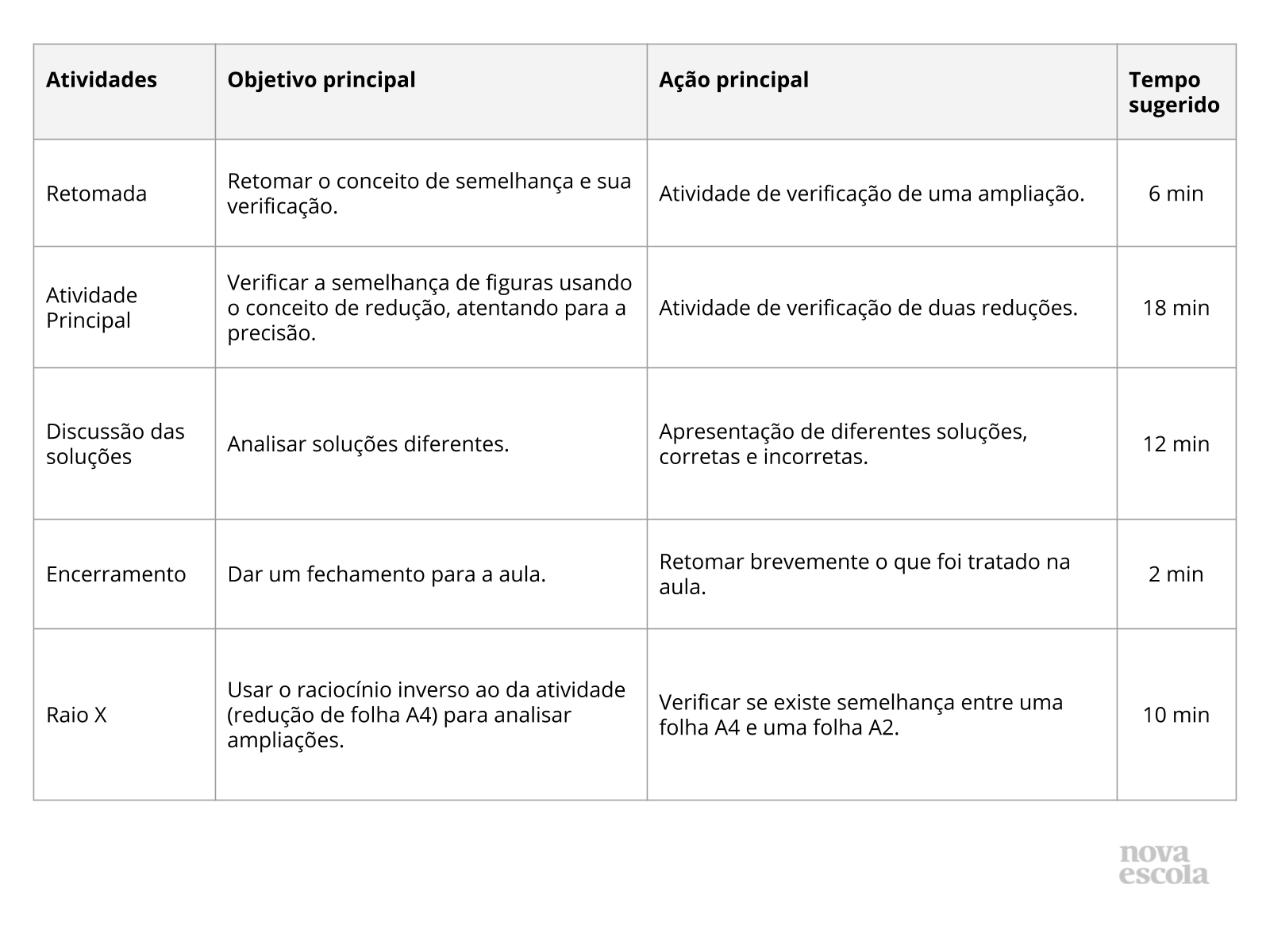
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo da aula

Tempo sugerido: 2 minutos
Orientação: Apresentar o objetivo da aula para os alunos. O objetivo pode ser apresentado na lousa com o slide, pode ser escrito na lousa ou pode ser apenas falado pelo professor.
Propósito: Fazer com que os alunos fiquem em estado de prontidão para a aula.
Observando de perto

Tempo sugerido: 6 minutos
Objetivo:
Retomar o conhecimento de semelhança de polígonos.
Propósito:
Fazer com que os alunos se lembrem do conteúdo que será tratado nesta aula (semelhança aplicada a polígonos).
Discuta com a turma:
- Se é maior e parecido com a figura original, é ampliação?
- O que é necessário para que duas figuras sejam ampliação?
- Como eu verifico se é ampliação?
Materiais complementares para impressão:
Aquecimento
Resolução do Aquecimento
Razões
Tempo sugerido: 18 minutos
Orientação:
Divida a sala em grupos de até 4 alunos. Cada grupo receberá duas folhas de sulfite. Em uma das folhas eles devem colocar seus nomes (e qualquer outra identificação que você considere importante).
Diga aos alunos que na folha com seus nomes eles deverão fazer a representação de cada etapa da parte prática da atividade, incluindo as medidas a cada momento.
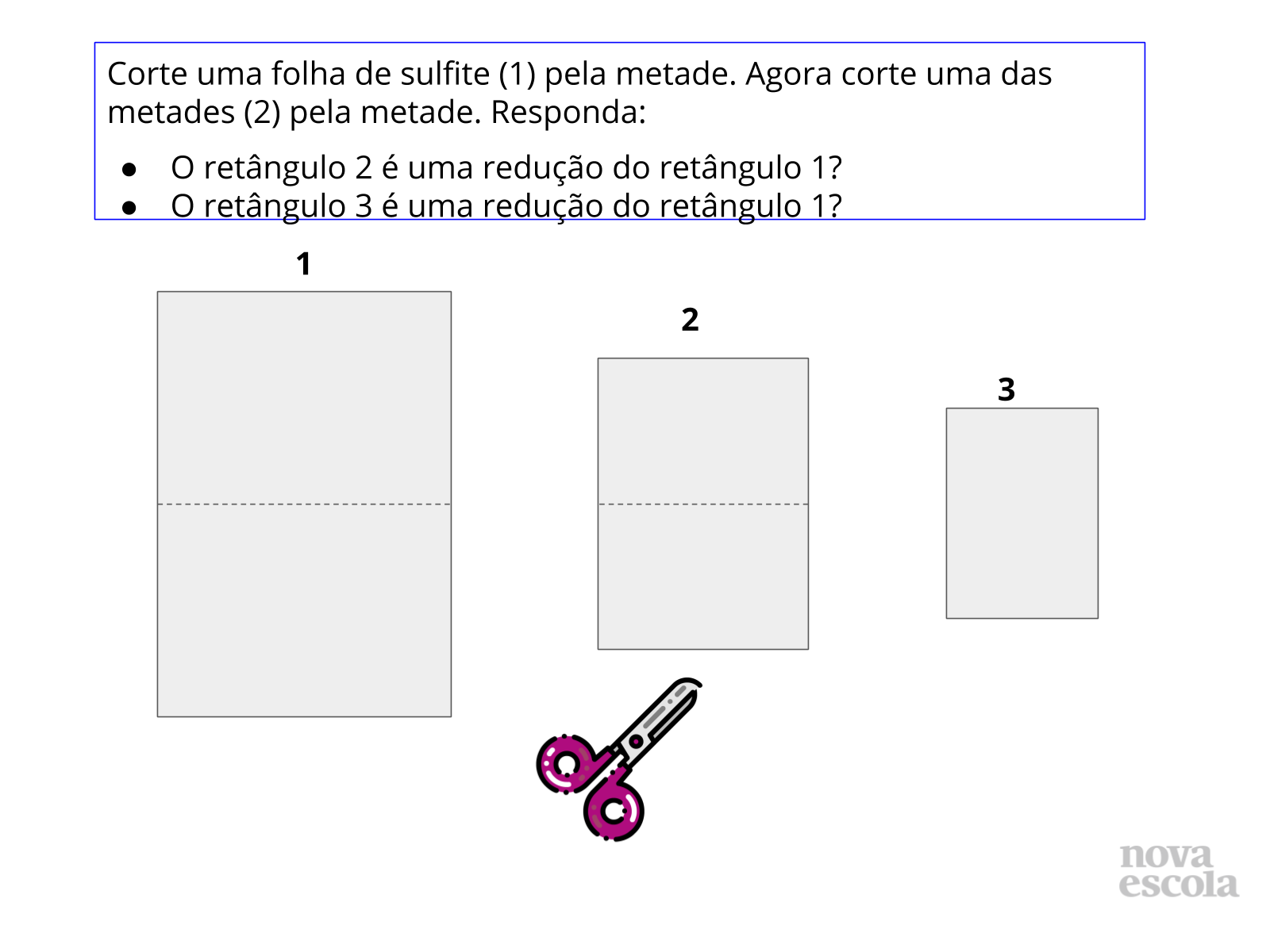
Primeiramente, eles devem desenhar uma representação da folha de sulfite (não há necessidade de um desenho proporcional, trata-se de uma representação e as medidas serão dadas ao lado da figura). Dentro dessa figura eles deverão escrever o número 1. Agora eles deverão considerar um dos lados como base e o outro como altura (essa escolha é arbitrária e o resultado independe da ordem, mas é interessante que os alunos percebam isso, então, se eles perguntarem que lado é a base e que lado é a altura diga que eles podem decidir isso). Ao lado da figura 1 eles irão anotar as medidas de sua base e altura.
Feito isso, eles irão dividir a folha de sulfite ao meio (dividir o lado maior ao meio) e novamente farão a representação desse novo retângulo, dentro deste retângulo estará o número 2. Eles anotarão ao lado as medidas da base e da altura (se eles usaram, por exemplo, o lado menor como base devem fazer a mesma coisa com o retângulo 2). Eles farão mais uma divisão desse retângulo 2 (tomando o cuidado de dividir o lado maior ao meio) e repetirão o procedimento para esse retângulo 3.
Agora você vai querer que eles verifiquem que o retângulo 2 não é semelhante ao retângulo 1 e, portanto não é uma redução do mesmo. O mesmo não acontece com o retângulo 3, em relação ao retângulo 1. O retângulo 3 é uma redução do retângulo 1 com razão ½. Isso acontece porque o lado maior do retângulo 3 é igual a metade do lado maior do retângulo 1 e o lado menor do retângulo 3 é igual à metade do lado menor do retângulo 1.
Propósito:
Estudar redução usando semelhança de polígonos.
Discuta com a turma:
- Quando eu corto uma folha qualquer no meio, qual a relação entre seus lados e os lados da folha original?
- E se eu cortar no meio mais uma vez, qual a relação entre seus lados e os da folha original?
Materiais complementares para impressão:
Atividade para impressão
Resolução da atividade
Guia de intervenção
Soluções
Tempo sugerido: 12 minutos.
Orientação:
Se possível, apresente soluções dos alunos, os erros que apareceram, para que façam parte da discussão. As três soluções apresentadas no slide são as mais comuns. Vamos discutir cada uma:
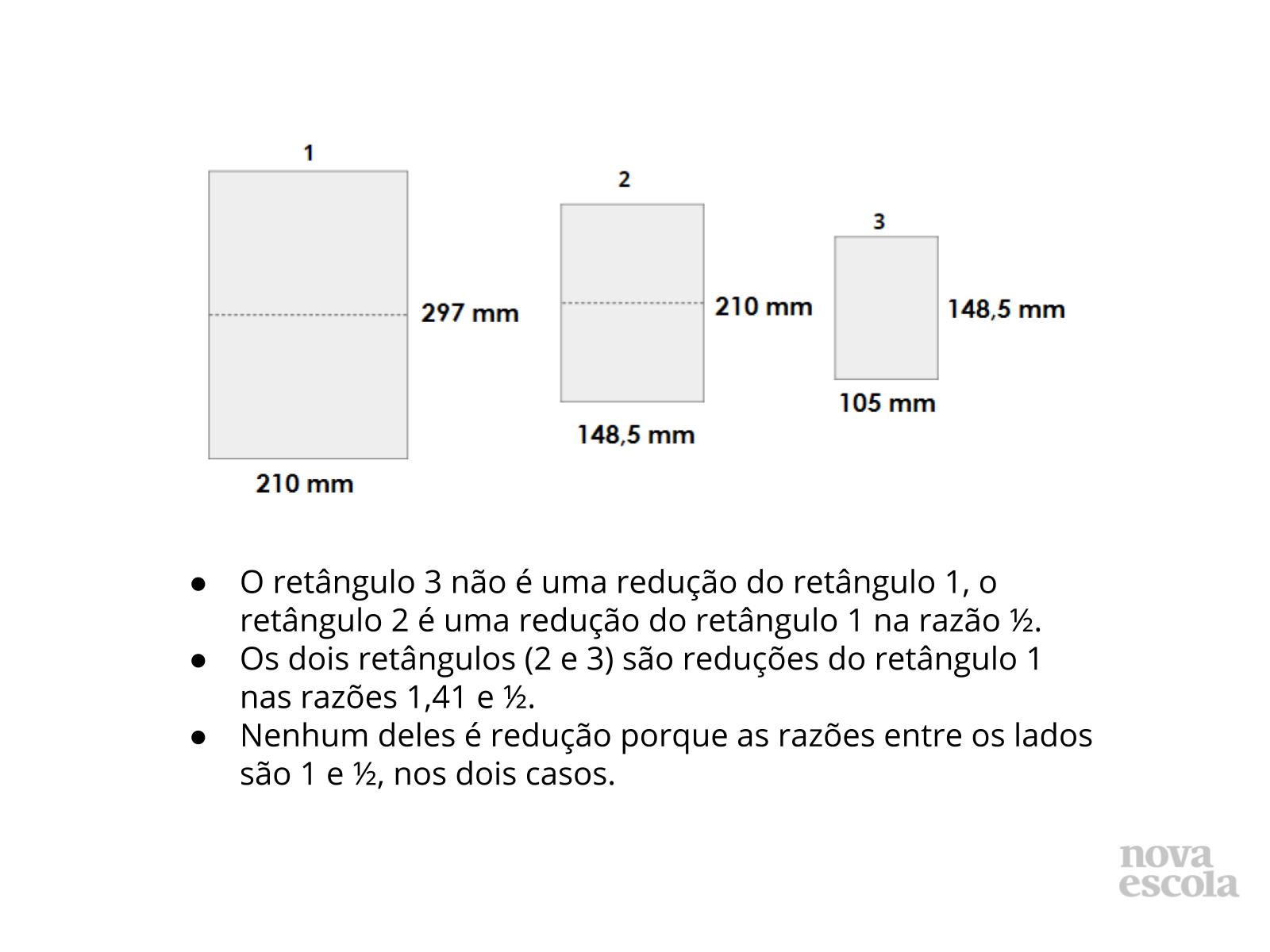
- O retângulo 2 não é uma redução do retângulo 1, o retângulo 3 é uma redução do retângulo 1 na razão ½.
Essa é a solução correta. As razões entre os lados correspondentes dos triângulos 1 e 2 são valores muito parecidos, mas diferentes (1,4142857... e 1,41… - dízimas periódicas com períodos 142857 e 41, respectivamente). Cabe aqui uma discussão sobre precisão na matemática.
- Os dois retângulos (2 e 3) são reduções do retângulo 1 nas razões 1,41 e ½.
Essa solução não está correta, está imprecisa. O aluno que responde desta forma sabe o que é semelhança, sabe como calcular a razão entre os lados das figuras semelhantes, mas não considera a precisão importante na resposta. A discussão da resposta anterior já engloba essa resposta, mas é importante ressaltar o que o aluno fez de correto.
- Nenhum deles é redução porque as razões entre os lados são 1 e ½, nos dois casos:
Essa solução é encontrada quando consideramos os lados correspondentes de forma incorreta. Comparando os retângulos 2 e 1, se compararmos o lado maior de 1 com o lado menor de 2, teremos razão ½, se compararmos o lado menor de 1 com o lado menor de 2, teremos razão 1. Comparando o retângulo 3 com o retângulo 1, comparando o lado maior com o menor, teremos razão ½ e comparando o menor com o maior, teremos razão 1. “Para comparar os dois eu tenho que comparar altura com altura e base com base. Qual é a altura desses retângulos?”
Propósito:
Fazer com que o aluno perceba que há diferentes formas de solucionar um problema matemático e que mesmo uma resposta incorreta pode levar a uma melhor compreensão do problema.
Encerramento

Tempo sugerido: 2 minutos.
Orientação: Retomar brevemente o que foi tratado neste aula.
Propósito: Dar um fechamento à aula.
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 

















