Guia de intervenção
Plano de Aula
Plano de aula: O mínimo de números, o máximo de lógica!
Plano 2 de uma sequência de 10 planos. Veja todos os planos sobre Resolução e Elaboração de Problemas.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Wasley Antonio Ronchetti
Mentora: Eunice Maria Figueira Cajango
Especialista de área: Rita de Cássia Batista da Silva
Objetivos específicos
- Estruturar a organização do pensamento lógico, valorizando estratégias diversificadas de resolução.
- Desenvolver ações de justificar e argumentar na resolução de problemas de lógica;
- Determinar os procedimentos necessários para a resolução de problemas de lógica.
Conceito-chave
Lógica matemática
Recursos necessários
Lápis, papel, borracha, materiais impressos
Vocabulário que será aprendido nesta aula
lógica matemática com dados numéricos
Habilidades BNCC:
Objetivos de aprendizagem
- Estruturar a organização do pensamento lógico, valorizando estratégias diversificadas de resolução.
- Desenvolver ações de justificar e argumentar na resolução de problemas de lógica;
- Determinar os procedimentos necessários para a resolução de problemas de lógica.
Resumo da aula - O mínimo de números, o máximo de lógica
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: Apresentar aos alunos problemas de lógica matemática que trazem dados numéricos
Propósito: Apresentar para a turma o objetivo da aula.
Aquecimento

Tempo sugerido: 8 MINUTOS
Orientação: Professor, inicie esta atividade retomando os conceitos de lógica dedutiva, abordados no plano conceitual. Inicie perguntando se toda situação-problema precisa ter número para ser considerada um problema de matemática. Peça que relatem de forma breve conhecimentos, fatos ou habilidades que se relacionam com tais termos (“problema de lógica” “pensamento lógico dedutivo”). Caso ache interessante, faça um esquema no quadro com a palavra lógica ou lógica dedutiva e vá traçando ramificações baseadas nas respostas dos alunos.
Propósito: Retomar os conceitos de lógica dedutiva e de pensamento lógico dedutivo.
Discuta com a turma:
- Existe uma única forma de resolver problema de lógica?
- Qual você considera a melhor estratégia para organizar seu pensamento durante a resolução deste tipo de problema?
- Você acha que o termo dedutivo faz sentido? A que você entende que essa palavra se refere?
Atividade principal

Tempo sugerido: 12 minutos
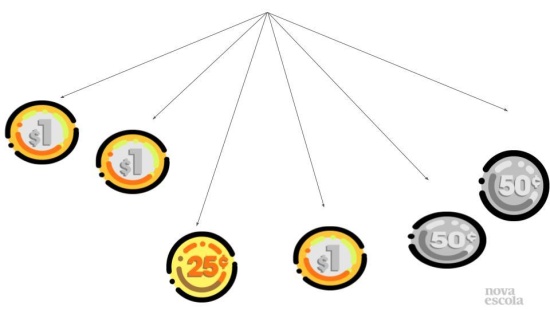
Orientações: Faça a leitura da atividade juntamente com os alunos. Esta atividade poderá ser escrita no quadro, projetada ou impressa e distribuída aos alunos. O próximo passo é que cada um faça a leitura individualmente e comece a buscar suas soluções para este problema. Depois organize a turma (da maneira que julgar mais adequada) para que juntos discutam sobre as estratégias traçadas por eles para a resolução do problema.
Propósito: Buscar estratégias que permitem a resolução do problema proposto.
Materiais complementares para impressão:
Discussão da solução

Tempo Sugerido: 20 minutos
Orientação: Professor, este momento deve ser apresentado aos alunos, somente após as discussões e apresentações realizadas pelos mesmos. Permita que os grupos formados exponham para a sala as maneiras que buscaram as estratégias utilizadas na resolução e seus pensamentos. Se possível estimule que demonstrem no quadro (essa exposição deve ser realizada em grupo, uma vez que individualmente tomaria muito tempo) os procedimentos que utilizaram . Nos slides seguintes, apresentamos algumas possibilidades de resolução que podem ser apresentadas pelos alunos (caso as estratégias de resolução apresentadas pelos alunos, sejam idênticas a dos slides, não há necessidade de apresentação dos slides. Valorize a apresentação dos alunos).
Propósito: Apresentação das estratégias utilizadas para resolver um problema de lógica matemática
Discuta com a turma: Durante a exposição das estratégias dos alunos, promova discussões com eles. Realize algumas perguntas e caso algum aluno queira perguntar, faça essas mediações entre a turma. Abaixo estão algumas perguntas que servirão para realizar as discussões com os alunos.
- Vocês sentiram alguma dificuldade em resolver este problema? Quais?
- O que mais chamou sua atenção na resolução deste problema?
- Você consegue lembrar de algum outro problema de lógica que ja tenha resolvido? Caso você ja tenha feito e se recorde, consegue fazer apontamentos se há diferenças ou semelhanças entre eles? No que se assemelham? E no que se diferem?
Discussão da solução

Tempo sugerido: 20 minutos
Orientação: As resoluções propostas só devem ser apresentadas depois de realizada as discussões com os alunos, sobre as estratégias utilizadas por ele eles na resolução.
Propósito: Apresentar e discutir as possíveis resoluções da atividade proposta.
Discussão da solução

Tempo sugerido: 20 minutos
Orientação: As resoluções propostas só devem ser apresentadas depois de realizada as discussões com os alunos, sobre as estratégias utilizadas por ele eles na resolução.
Propósito: Apresentar e discutir as possíveis resoluções da atividade proposta.
Discussão da solução

Tempo sugerido: 20 minutos
Orientação: As resoluções propostas só devem ser apresentadas depois de realizada as discussões com os alunos, sobre as estratégias utilizadas por ele eles na resolução.
Propósito: Apresentar e discutir as possíveis resoluções da atividade proposta.
Discussão da solução
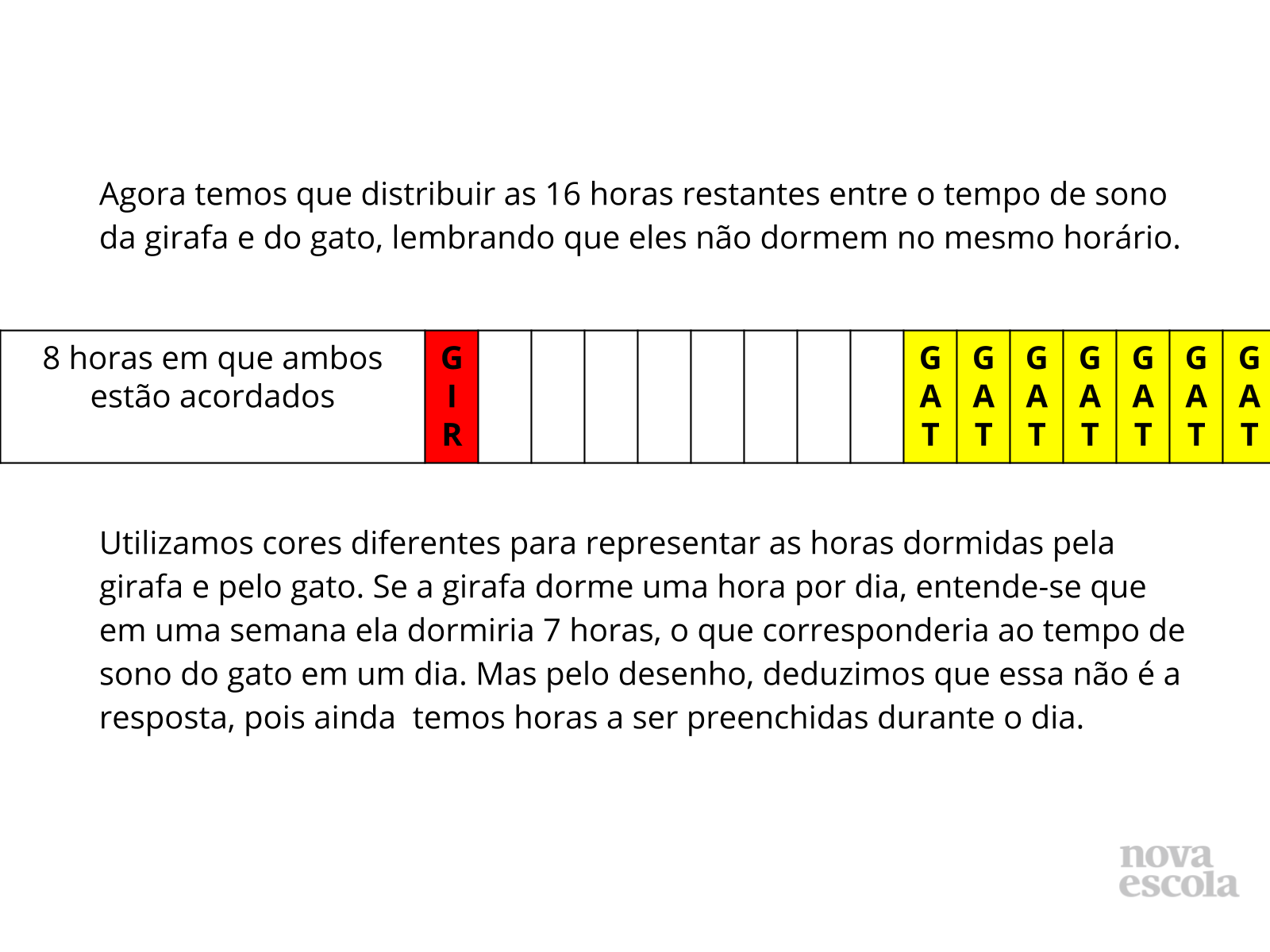
Tempo sugerido: 20 minutos
Orientação: Professor, seria interessante nesta atividade fazer uma abordagem da divisão do tempo em partes iguais, o que implicaria em revisar com a turma o conhecimento sobre: resolução de problemas com diferentes significados na multiplicação e divisão (proporcionalidade , repartição em partes iguais e medida (EF04MA06 e EF04MA07) e Identificação, representação numérica, visual e aplicação em diversos contextos de frações unitárias usuais (EF04MA09). Sob tal perspectiva, aborde que durante as 24 horas de um dia, é possível fazer três grupos de 8 horas, e cada período de 8 horas, equivale a ? desse dia. Trabalhe a ideia de que o dia com suas 24 horas é o todo, e que esse todo pode ser repartido em três partes iguais e que cada parte corresponde a um terço.
Propósito: Apresentar e discutir as possíveis resoluções da atividade proposta.
Discuta com a turma:
- Existem outras formas de dividir um dia em partes iguais? Quais?
- Quando um médico receita um medicamento, ele geralmente recomenda que cada dose do remédio seja administrada de 4 em 4 horas, de 6 em 6 horas, de 8 em 8h, ou de 12h em 12h. Por que será que ele age assim?
- Caso o problema não apresentasse a informação de que os dois animais passam o mesmo tempo do dia acordados, como essa configuração poderia ser pensada?
Discussão da solução
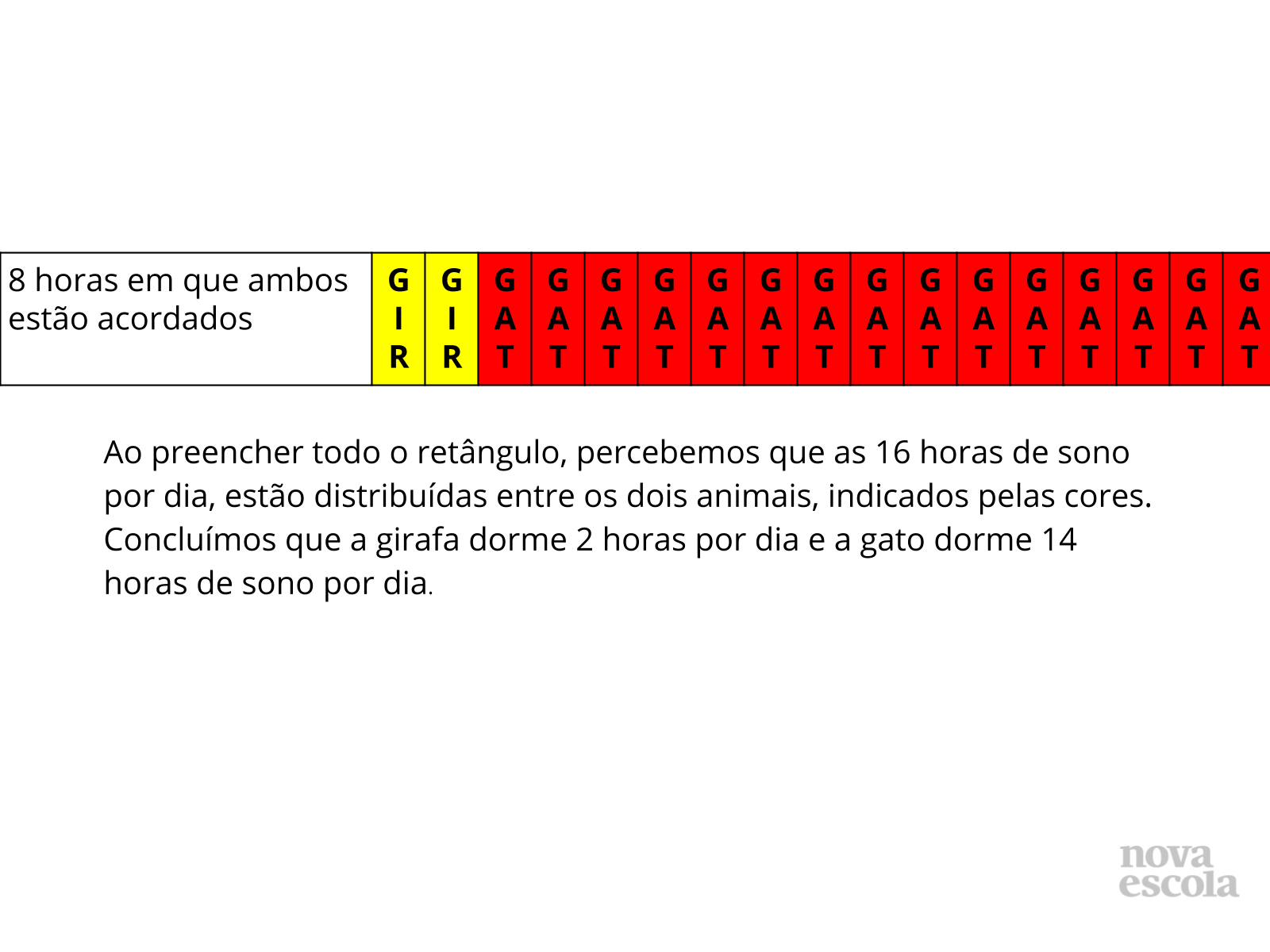
Tempo sugerido: 20 minutos.
Orientação: Professor, antes de iniciar as discussões, é interessante destacar que as informações apresentadas neste problema, são baseadas em dados científicos que podem ser obtidos em pesquisas realizadas pela internet ou em livros. Destaque a girafa é considerado o animal que menos dorme, e as informações sobre as horas de sono deste animal pode ser encontrada apresentando uma variação de 1,9 a 3 horas de sono por dia. O gato não é o animal que mais dorme, mas é um dos que mais dormem. O total de horas de sono deste animal, também varia de 14 a 16 horas, de acordo com a fonte consultada. O guia de intervenção traz os sites consultados, de forma que poderá servir de consulta para outras atividades.
Apresentada as resoluções da atividade principal, promova com seus alunos uma discussão sobre a mesma. Leve-os a entender que o problema no seu enunciado colocava algumas condições ou restrições que deveriam ser atendidas para se chegar a resposta. Evidencie que tais restrições são as informações de que o gato e a girafa dormem em horários diferentes, o que nos permite apresentar a resposta. Feitas essas considerações, promova a discussão com os alunos.
Propósito: Apresentar e discutir as possíveis resoluções da atividade proposta.
Discuta com a turma:
- E se o problema não afirmasse que eles dormem em períodos diferentes do dia, seria possível oferecer uma resposta exata ou uma resposta única à pergunta? Por quê?
- A informação que foi fornecida no texto sobre as horas que eles passam acordados, foi importante pra resolver o problema? Em que ela ajudou?
- É possível afirmar que todas as girafas e todos os gatos dormem essa quantidade de horas por dia? Justifique sua resposta.
Encerramento

Tempo sugerido: 2 minutos.
Orientação: Encerre a aula destacando algumas características comuns aos problemas de lógica matemática.
Enfatize que problemas desse tipo utilizam o raciocínio lógico, que é uma forma de pensar que exige de nós a organização das ideias e uma forma diferenciada de estruturar as informações, e que esse tipo de habilidade só é adquirida quando praticamos constantemente a resolução desse tipo de problema.
Destaque que a busca por diferentes estratégias de resolução, traçando ideias que podem dar certo ou errado, é o processo natural de resolução de problemas dessa natureza. Por fim, não deixe de mencionar que a resolução de problemas de lógica matemática permitem relacionar conteúdos já estudados por eles.
Propósito: Discutir com os alunos sobre os problemas de lógica matemática e as estratégias utilizadas na resolução das atividades propostas.
Raio X

Tempo sugerido: 8 MINUTOS
Orientação: Apresente este problema aos alunos e peça que pensem nas maneiras que podem obter a resolução . Professor, você pode apresentar este problema no quadro, por meio da projeção ou pode providenciar cópias para os alunos. Esta atividade de raio x servirá para avaliar as aprendizagens dos alunos e verificar se compreenderam a maneira de resolver problemas que utilizam a lógica matemática. É de fundamental importância a sua atenção neste momento, para que possa fazer suas intervenções.
Propósito: Verificar se os alunos compreenderam a resolução de problemas de lógica matemática envolvendo dados numéricos.
Discuta com a turma:
- Com relação às atividades que realizamos hoje, o que podemos observar sobre as várias maneiras que um problema de matemática pode ser proposto?
- É possível estabelecer alguma relação desses problemas com situações cotidiana?
- O que mais chama atenção na resolução desses problemas?
Materiais complementares para impressão:
Raio X

Tempo sugerido: 8 MINUTOS
Orientação: Buscar diferentes estratégias que permitam a resolução da atividade.
Propósito: Resolver a atividade de raio x
Sugestão de adaptação para ensino remoto
Código do plano MAT5_26RDP02
Recursos
- Necessários: -
- Opcionais: -
Para este plano, foque na etapa Aquecimento, Atividade principal e Discussão das soluções
Aquecimento
Professor(a), você pode realizar o Aquecimento deste plano com seus alunos, seja em uma aula síncrona ou assíncrona. Compartilhe com a turma o slide presente nesta atividade e discuta com os alunos as respostas por eles apresentadas. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas reflexões, questionamentos e conversem entre si, mas caso esteja ocorrendo de forma assíncrona, os estudantes podem enviar suas considerações/reflexões em formato de texto ou áudio.
Atividade principal
Professor(a), compartilhe com a turma os slides presentes nesta etapa do plano de aula e solicite que tentem resolver o problema. Você pode encontrar o documento com a atividade aqui: https://nova-escola-producao.s3.amazonaws.com/cgHMWp74A9MfJazSPj9jMBWtSBkQnzx3t6h5vrSGSnxHtJj5UCzkaktbrCFQ/ativprinc-mat5-26rdp02.pdf. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas resoluções e, caso esteja ocorrendo de forma assíncrona, os estudantes podem enviar suas resoluções/explicações em formato de texto ou áudio.
Discussão das soluções
Professor(a), nesse momento de aulas remotas, talvez, não seja a melhor estratégia deixar a interpretação da “Discussão das soluções” para os alunos. Portanto, caso considere viável compartilhar os slides com os estudantes, considere realizar a explicação de cada etapa. Caso a aula esteja ocorrendo de forma assíncrona, sugerimos que você grave um vídeo explicando as soluções e nele apresente os slides. Os slides presentes nesta etapa da aula, se compartilhados sem explicação, podem confundir os alunos visto que eles podem ter utilizado diferentes estratégias. Você pode pedir que os alunos gravem vídeos explicando uma suas soluções. Para instigar a resolução de problemas de lógica você pode sugerir que os alunos visitem o site Racha Cuca e joguem problemas que trabalhem o raciocínio lógico, segue o link: https://rachacuca.com.br/logica/problemas/
Raio X
O problema proposto no Raio X pode ser enviado para os alunos e solicitado como uma “tarefa” a ser entregue em momento a ser combinado com a turma.
Convite às famílias
Professor(a), sugira que os alunos socializem com seus familiares o que aprenderam nesta aula sobre problemas de lógica. Sugira que os alunos mostrem a seus familiares o problema proposto no Raio X e que eles compartilhem suas estratégias para resolvê-lo. Você pode sugerir que os estudantes apresentem os problemas presentes em https://www.mundosimples.com.br/quiz-exercicios-logica-matematica-volume1.htm aos seus familiares e que eles tentem refletir e resolvê-los juntos ou então jogarem algum dos jogos de https://rachacuca.com.br/logica/problemas/.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Wasley Antonio Ronchetti
Mentora: Eunice Maria Figueira Cajango
Especialista de área: Rita de Cássia Batista da Silva
Objetivos específicos
- Estruturar a organização do pensamento lógico, valorizando estratégias diversificadas de resolução.
- Desenvolver ações de justificar e argumentar na resolução de problemas de lógica;
- Determinar os procedimentos necessários para a resolução de problemas de lógica.
Conceito-chave
Lógica matemática
Recursos necessários
Lápis, papel, borracha, materiais impressos
Vocabulário que será aprendido nesta aula
lógica matemática com dados numéricos