Guia de intervenções
Plano de Aula
Plano de aula: Semelhança de Triângulos
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Ampliação e redução de figuras planas em malhas quadriculadas
Por: Paula Vieira Soares
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Paula Vieira Soares
Mentora: Renata S. Gonçalves
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
EF06MA20 - Construção de figuras semelhantes: ampliação e redução de figuras planas em malhas quadriculadas.
Objetivos específicos
Verificar os casos de semelhança de triângulos, através do estudo de ampliações e reduções.
Conceito-chave
Semelhança de Triângulos
Recursos necessários
- Régua;
- Papel sulfite;
- Tesoura
- Varetas (para construir pipas) - pode ser usado palito de churrasco, canudos, mas quanto mais fino o material, maior a precisão da construção dos alunos.
- Papel cartão ou cartolina.
Sugestões de Leitura
FERREIRA, Anna Rachel. O desafio de organizar e mediar o trabalho em grupo. Nova Escola: Prática Pedagógica, 19 de Abril. 2017 - Disponível em: https://goo.gl/dAQqbP (visitado em 02/12/2017)
MACHADO, Nílson José. Semelhança não é mera coincidência - (Coleção Vivendo a Matemática). Scipione, 2000.
BOALER, Jo. Mentalidades Matemáticas. 1ª ed. Porto Alegre - RS. Penso, 2018
DOLCE, Osvaldo. POMPEO, José Nicolau. Fundamentos da Matemática. Volume 9 - Geometria Plana. São Paulo - SP. Atual, 2005.
Conhecimentos que a turma deve dominar:
- Noção de semelhança de polígonos.
Habilidades BNCC:
Objetivos de aprendizagem
Verificar os casos de semelhança de triângulos, através do estudo de ampliações e reduções.
Resumo da aula
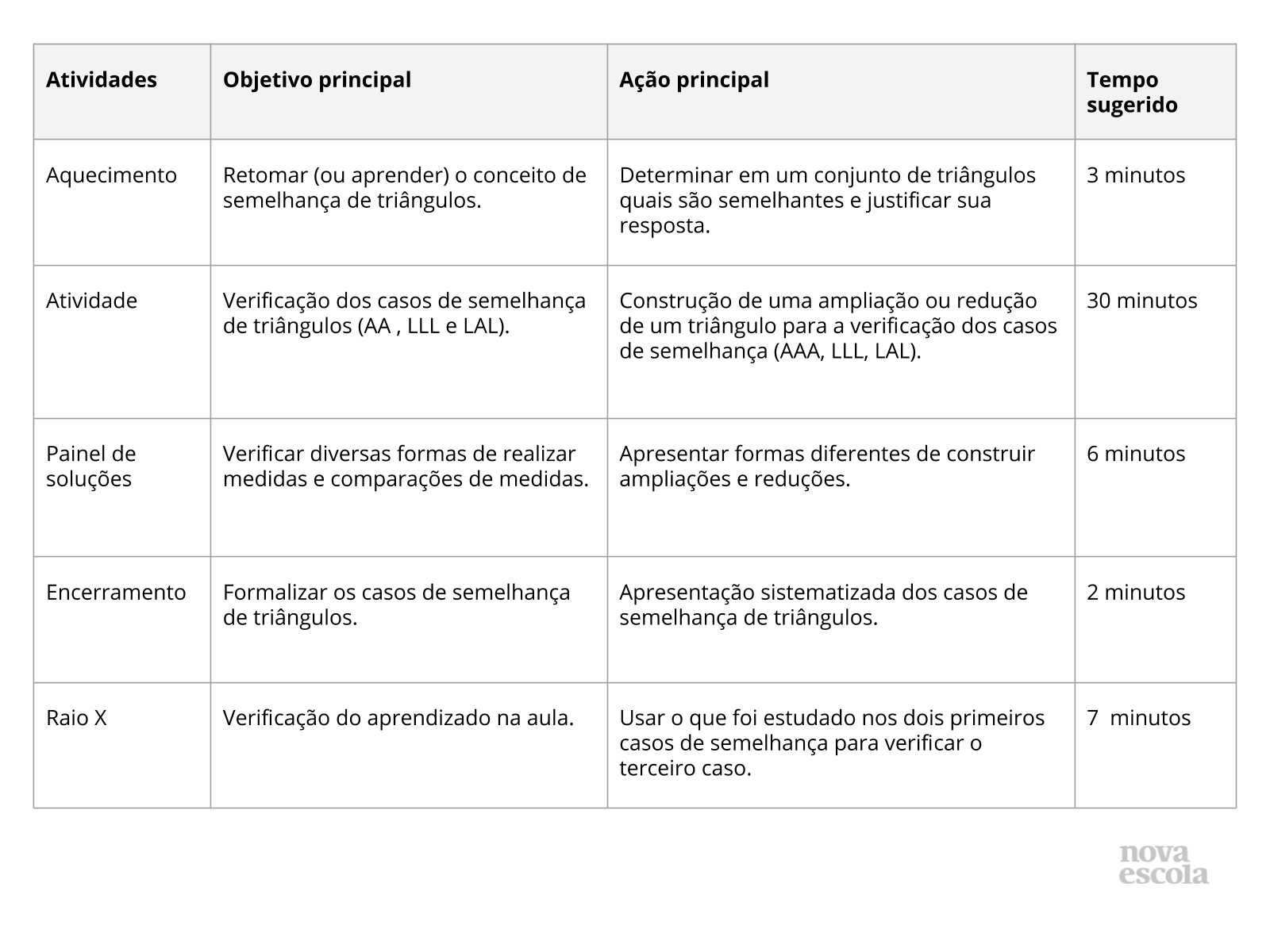
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo da Aula

Tempo sugerido: 2 minutos.
Orientação: Apresentação do objetivo da aula para os alunos.
Propósito: Deixar os alunos de prontidão para o conteúdo da aula.
Aquecimento
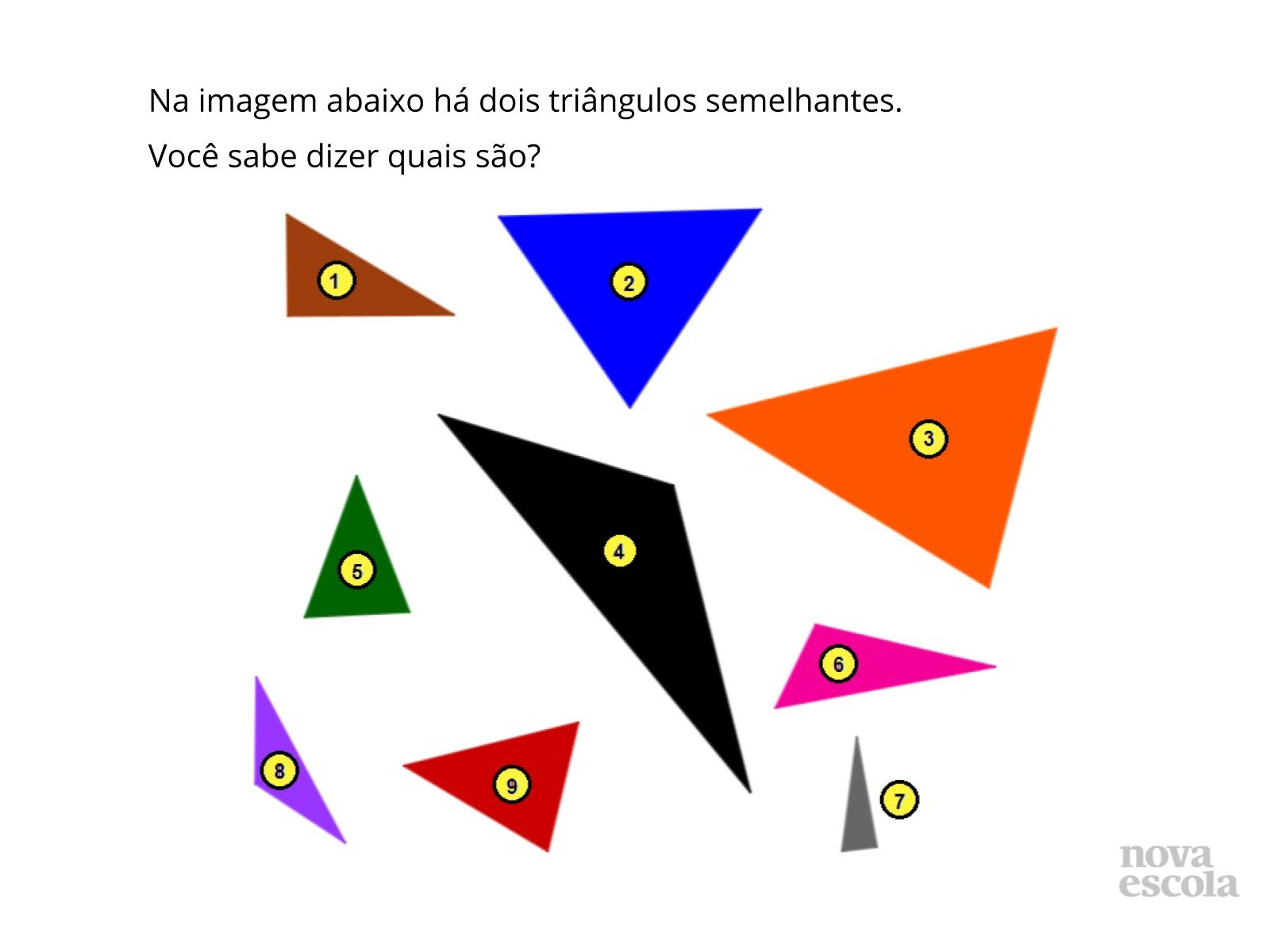
Semelhanças
Tempo sugerido: 3 minutos.
Orientação: Discuta com os alunos a ideia de semelhança (neste caso, semelhança de triângulos). A discussão pode ser feita com a sala toda. Os triângulos 3 e 9 são os únicos triângulos semelhantes. Há alguns parecidos (como 4 e 6) e essa é uma motivação para discutir o conceito matemático de semelhança. A idéia é apontar para os alunos que dois triângulos só são semelhantes matematicamente se seus lados são proporcionais e seus ângulos são congruentes. Não há necessidade de aprofundar essa idéia nesse momento porque ela será tratada mais detalhadamente nas atividades apresentadas a seguir.
Propósito: Iniciar a discussão e retomar o conteúdo a ser estudado: Semelhança de triângulos.
Discuta com a turma:
- Os triângulos 4 e 6 são bem parecidos, mas não são matematicamente semelhantes. Por que vocês acham que isso acontece?
Materiais complementares para impressão:
Resolução da Atividade de Aquecimento
Atividade Principal
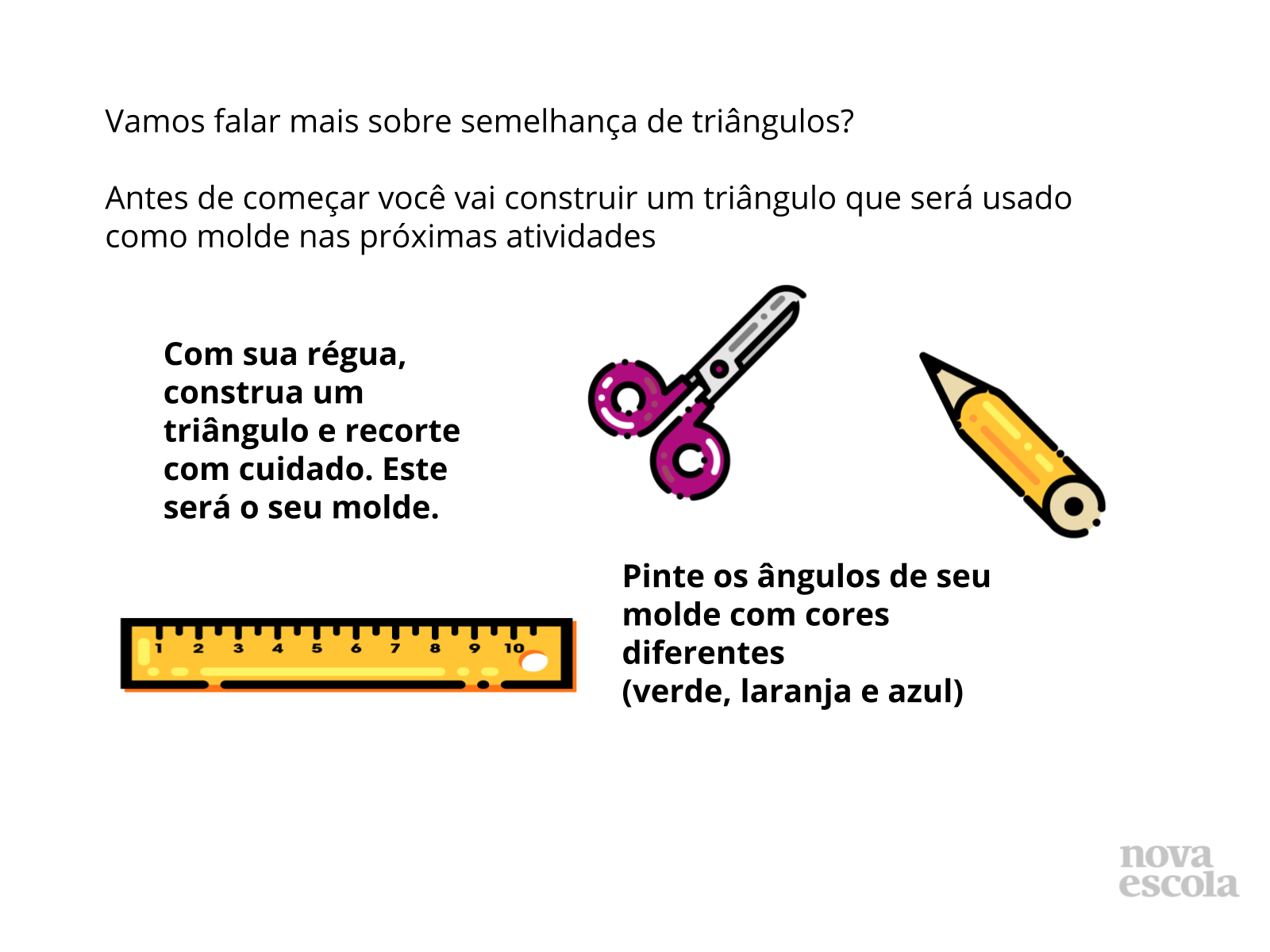
Semelhanças
Tempo sugerido: 2 minutos.
Orientação: Forme grupos de até quatro alunos. Distribua para cada grupo uma tesoura, um pedaço de cartolina e uma régua. Peça que tomem cuidado ao manusear o molde porque ele será usado para outras construções e, portanto, seus lados e ângulos devem estar firmes.
Propósito: Inicie a discussão e retome o conteúdo a ser estudado: Semelhança de triângulos. Os triângulos não precisam ser iguais aos dos colegas. Pode-se recortar sem medir os lados. Os triângulos podem ser de qualquer tipo (isósceles, equilátero, escaleno). O mais fácil é o triângulo retângulo, porque pode-se considerar partes do canto da folha como sendo os dois catetos. Neste caso, qualquer corte diagonal será a hipotenusa.
Discuta com a turma:
- O que é necessário para que um polígono seja um triângulo?
Materiais complementares para impressão:
Atividade Principal
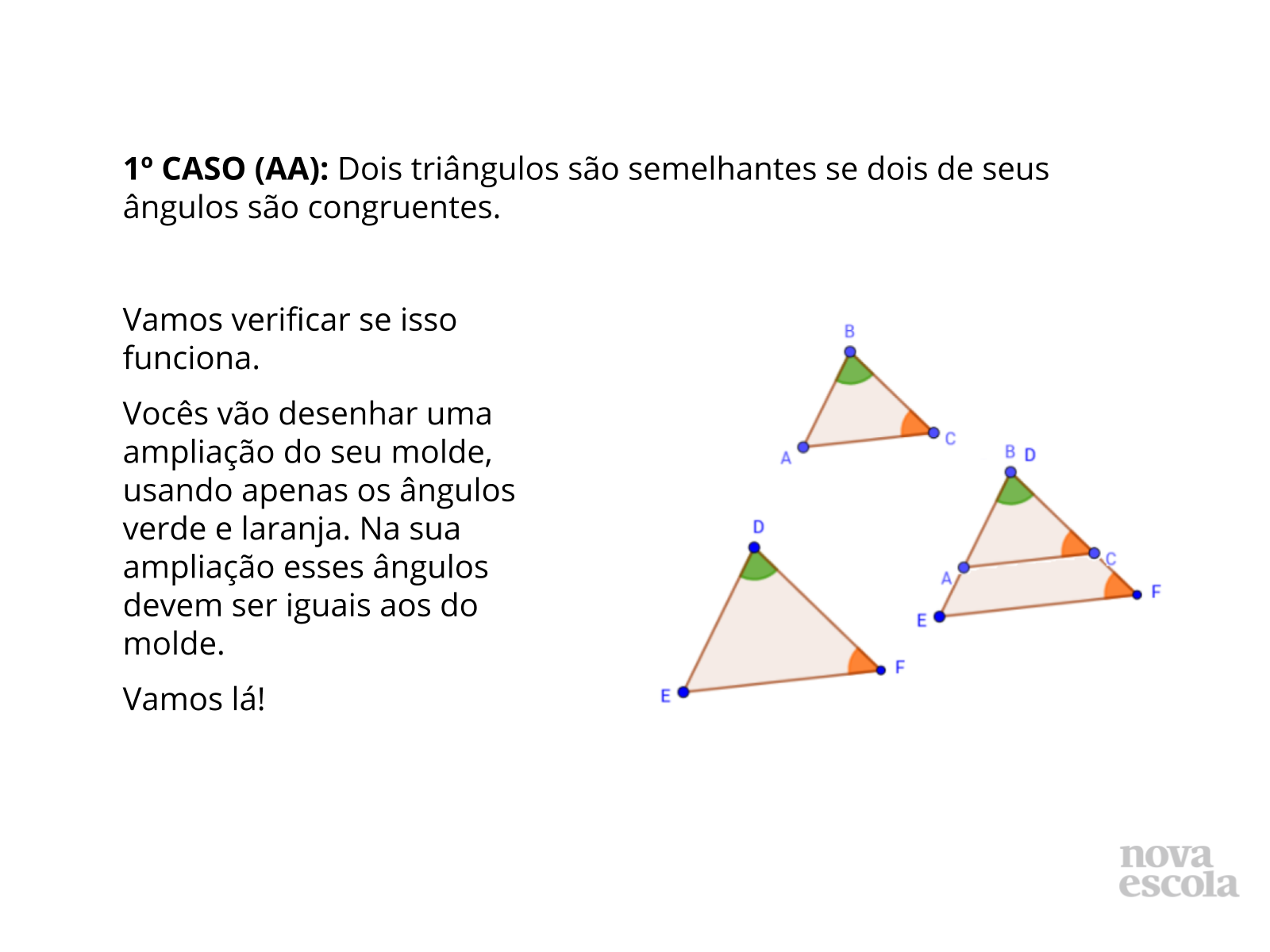
Semelhanças - Caso AA (dois ângulos congruentes)
Tempo sugerido: 10 minutos.
Orientação: A construção está detalhada na Resolução da Atividade. Queremos uma compreensão mais significativa dessa idéia através dos casos de semelhança de triângulos. Cada um garante a semelhança de dois triângulos sem a necessidade de observar todos os lados e ângulos. Nessa primeira situação, dois ângulos congruentes garantem que os triângulos sejam semelhantes. Os alunos vão verificar. Como fazer isso? Eles irão construir um triângulo semelhante ao molde usando apenas dois ângulos do molde original. Ao final, vão confirmar (ou não) se o triângulo construído e o molde são semelhantes.
Não há necessidade do uso de transferidor, mas se algum aluno quiser usar, não há problema (você pode deixar compasso, transferidor e esquadros disponíveis). A única proibição é copiar o próprio molde. O triângulo criado agora deve ser uma ampliação ou redução. Após a construção, eles deverão verificar se o triângulo construído é semelhante ao molde. Para isso, deve olhar se seus lados são proporcionais e encontrar a razão de semelhança. Devido ao erro implícito das medidas, os resultados não serão iguais, mas a aproximação deve ser boa (menor que 0,5 unidade).
Essa construção não é imediata. Eles devem primeiramente pensar na transferência dos ângulos para o papel.
“Observe um dos lados do seu molde. Como os ângulos estão posicionados nesse lado?”.
Propósito: Verificar que dois ângulos congruentes já garantem a semelhança entre dois triângulos, para aprofundar a compreensão do conceito de semelhança.
Discuta com a turma:
- Nós queremos desenhar um triângulo com dois ângulos iguais aos do molde. Por onde eu começo?
- Se eu quiser desenhar somente um dos ângulos, o que eu faço?
- Se eu tenho um ângulo e um lado, em que posição deverão estar os outros ângulos?
- Observe um dos lados do seu molde. Como os ângulos estão posicionados nesse lado?
- Após a construção, peça aos alunos que comparem o terceiro ângulo (que não foi construído) com o terceiro ângulo do molde (eles podem fazer isso usando o transferidor ou simplesmente colocando o terceiro ângulo do molde sobre o terceiro ângulo do triângulo construído. Questão: o que aconteceu com o terceiro ângulo? Posso dizer que, se eu tenho dois ângulos de um triângulo o terceiro já está determinado? Por que sim? (devido à soma dos ângulos internos de um triângulo ser sempre igual a 180º). Se os alunos disserem que não, pergunte Por que não?”; “Se não, por que isso vale para todos os triângulos diferentes da turma?”.
Guia de intervenção: https://goo.gl/4twGL2
Atividade principal para impressão: https://goo.gl/FY1gbh
Resolução da atividade principal: https://goo.gl/U9jnRi
Atividade Principal
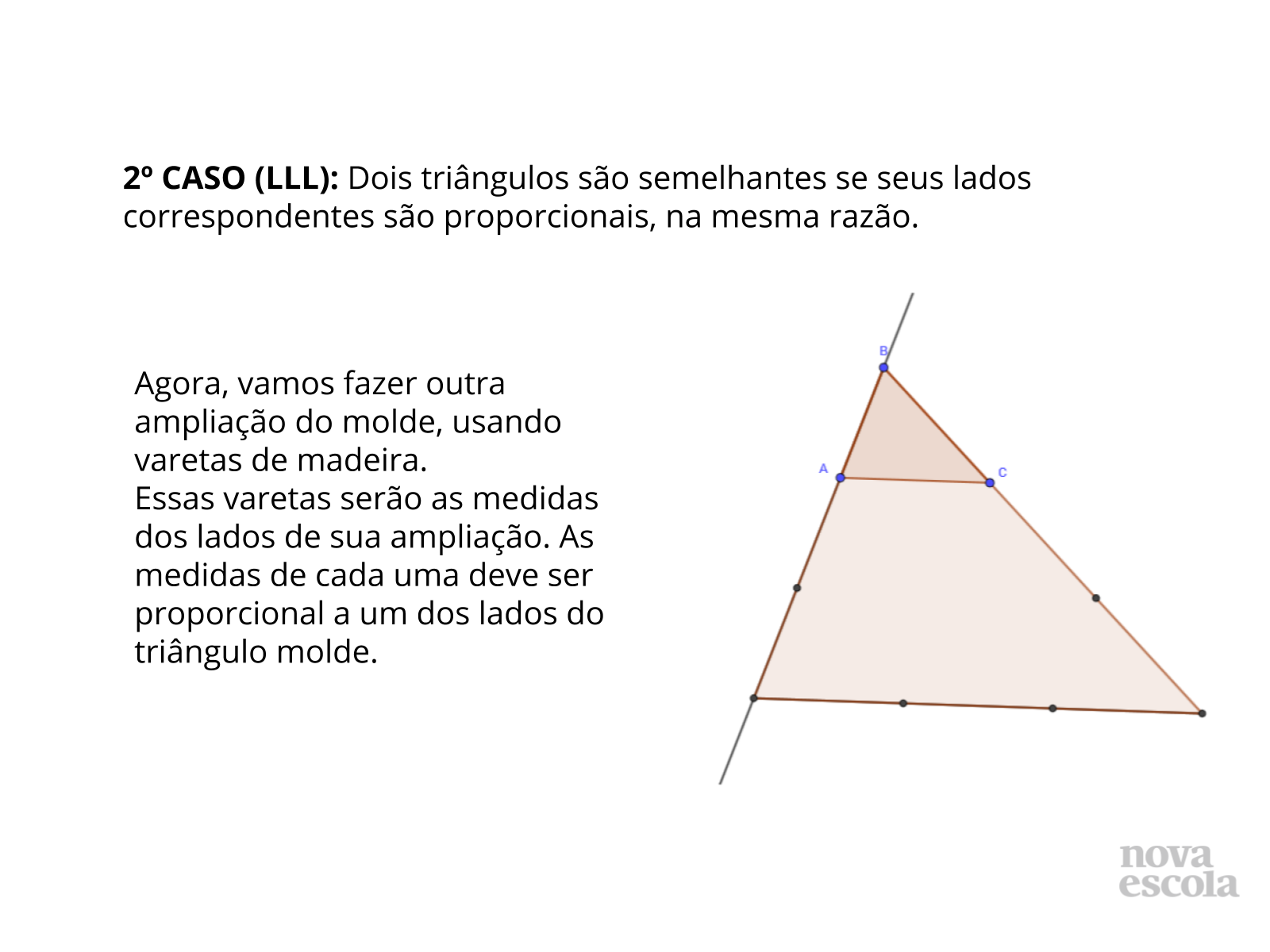
Semelhanças - Caso LLL (três lados com medidas proporcionais)
Tempo sugerido: 9 minutos.
Orientação: A construção está detalhada na Resolução da Atividade. Nesta construção, é importante que o aluno não se apoie nos ângulos para chegar ao resultado. O enunciado fala apenas dos lados e, se utilizamos os ângulos, não estaremos verificando o mesmo. O que pode ser um obstáculo para os alunos é a determinação da razão de semelhança e o cuidado de usá-la nos três lados construídos. Nessa atividade também não há necessidade de régua, mas o aluno poderá usar se entender que é o melhor. Usando apenas o molde como medida, as razões mais prováveis de aparecer são inteiras (2, 3, ..). Após as construções, peça que verifiquem se os ângulos são congruentes (os lados são semelhantes por construção). Para isso basta que “encaixem” os ângulos do molde nos ângulos correspondentes da figura construída.
A dificuldade dessa construção será garantir a mesma razão na proporção dos três lados. Uma forma de fazer isso é medir os lados do molde e cortar três varetas com o dobro (o triplo, o quádruplo,...) dessas três. Outra forma e usar o molde para marcar essa proporção nas varetas (duas vezes o lado do molde, três vezes o lado do molde,…). Se os alunos optarem por uma redução, podem marcar, por exemplo, a metade de cada lado (basta dobrar ao meio cada lado do molde) e cortar varetas com essas medidas.
Ao final eles devem unir as varetas para formar um triângulo. Eles devem traçar esse triângulo no papel. Os lados são proporcionais por construção, então eles só precisam verificar se os ângulos são congruentes. Para isso basta sobrepor cada ângulo do molde a seu correspondente na ampliação (ou redução).
Feito isso eles terão verificado que se os lados forem proporcionais isso já garante que os triângulos são semelhantes.
Propósito: Verificar que três lados correspondentes proporcionais já garantem a semelhança entre dois triângulos, para aprofundar a compreensão do conceito de semelhança.
Discuta com a turma:
- O que significa dizer que os lados devem ser proporcionais aos do molde?
- Digamos que essa caneta é um lado do meu molde e esse lápis é outro dos lados. Se eu fizer o lado equivalente ao da caneta com medida igual à medida de dez canetas, o quanto tem que medir o lado equivalente ao que é do tamanho do lápis?
- Lembre-se que cada vareta deve ser proporcional a um lado diferente.
Guia de intervenção: https://goo.gl/4twGL2
Atividade principal para impressão: https://goo.gl/FY1gbh
Resolução da atividade principal: https://goo.gl/U9jnRi
Atividade Principal
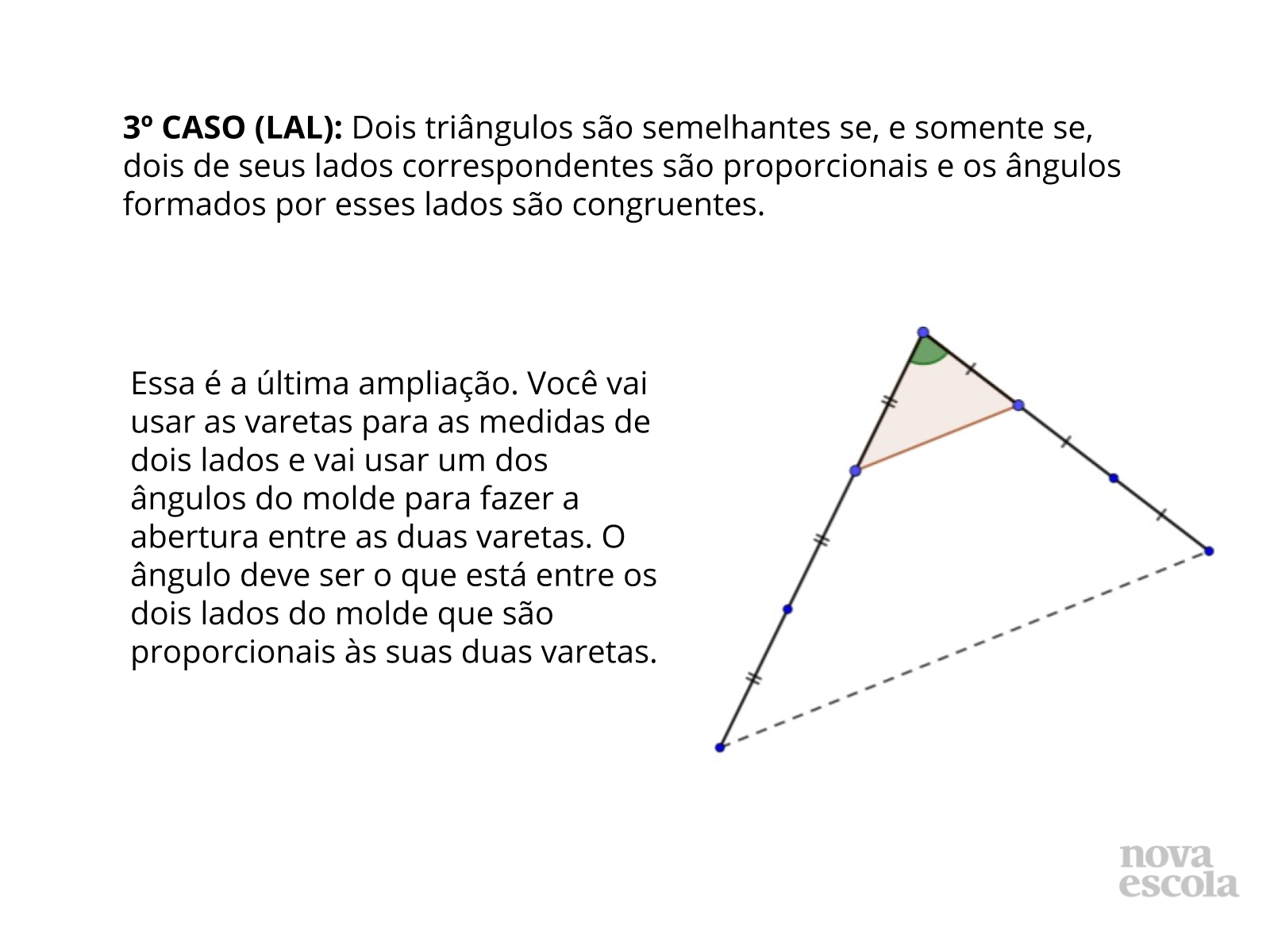
Semelhanças - Caso LAL (dois lados proporcionais e o ângulo entre esses lados congruente ao seu equivalente no molde)
Tempo sugerido: 9 minutos.
Orientação: A construção está detalhada na Resolução da Atividade. Eles já construíram lados proporcionais e já transferiram ângulos. Você já pode deixar por conta deles. Deixe que reflitam, testem, perguntem.
Depois que os alunos desenharem o triângulo na folha, é hora de conferir para ver se ele é realmente semelhante ao molde. Eles já sabem que dois lados são proporcionais, só precisam medir o terceiro lado e dividir pelo molde para saber se a razão é a mesma. Agora eles devem sobrepor os ângulos para ver se são todos congruentes.
Propósito: Verificar que dois lados proporcionais e os ângulos entre eles congruentes já garantem a semelhança entre dois triângulos, para aprofundar a compreensão do conceito de semelhança.
Discuta com a turma:
- Vocês têm que fazer dois lados proporcionais aos do molde. Vocês já fizeram isso na outra atividade. Como fizeram?
- Essas duas varetas correspondem a que lados do molde? Que ângulo esses lados formam?
- Como eu faço para que as varetas formem um ângulos iguais ao seu equivalente no molde? Se você tem dois lados e um ângulo, o que falta para eu construir um triângulo?
Guia de intervenção: https://goo.gl/4twGL2
Atividade principal para impressão: https://goo.gl/FY1gbh
Resolução da atividade principal: https://goo.gl/U9jnRi
Discussão das soluções

Formas diferentes de construir
Tempo sugerido: 6 minutos.
Orientação: Antes de apresentar os exemplos de solução, pergunte se algum aluno quer mostrar a sua. Se você percebeu alguma resolução diferente (mesmo que não chegue ao resultado correto), seria interessante que o aluno compartilhasse com os colegas. Quando apresentar os exemplos, pergunte se algum aluno fez algo parecido ou se fez algo totalmente diferente. Como não foi imposta nenhuma restrição, os moldes serão diferentes para cada grupo. É importante ressaltar que, em todos os grupos, o resultado foi condizente com os enunciados de cada caso. Também vale dizer que há formas diferentes de ampliações e reduções. Na discussão das soluções, há três exemplos que podem surgir em sua sala de aula.
Nesta etapa, o professor pode chamar a atenção para as diferentes formas de construção que podem ser usadas para resolver o problema. Em Matemática, de um modo geral, não há um único caminho para chegar ao resultado.
Propósito: Perceber que há diversos caminhos possíveis para resolver a questão, e que, portanto, não há uma regra rigorosa a ser seguida.
Discuta com a turma:
- As formas de resolução apresentadas levam a resultados diferentes?
- Considerar que uma é mais fácil que a outra é relativo. Se o aluno sente mais segurança com um procedimento que, a princípio, é mais complicado, este pode ser o procedimento mais fácil pra ele. Com o tempo eles poderão perceber as vantagens e desvantagens de cada procedimento em situações diferentes.
Encerramento
Tempo sugerido: 2 minutos.
Orientação: Aqui nós vamos dar um fechamento nas ideias tratadas na aula.
Retome o que foi estudado.
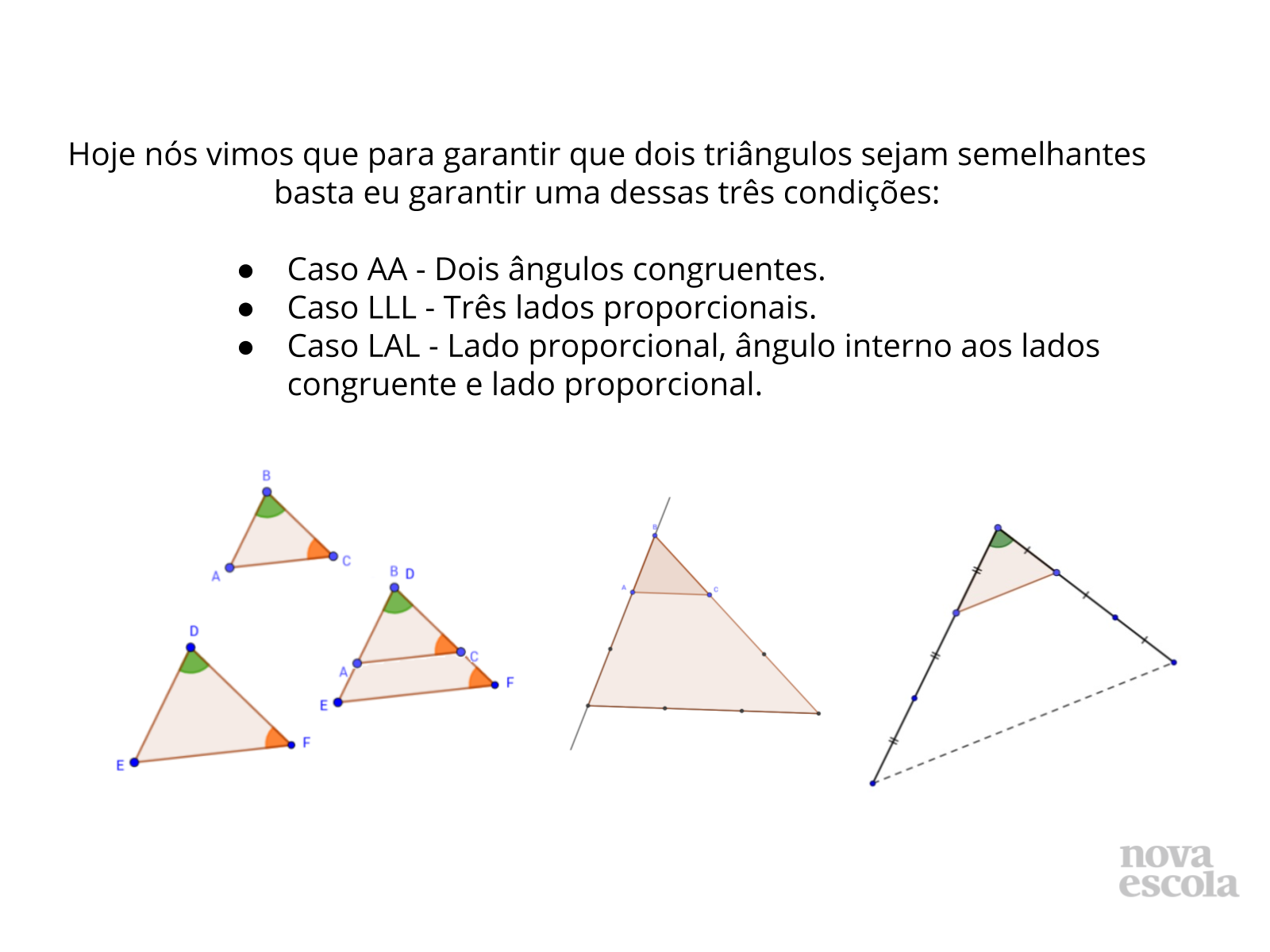
A ideia principal é que, para garantir que dois triângulos sejam semelhantes, não é preciso verificar todos os lados e ângulos dos dois triângulos. O primeiro caso diz que basta que dois ângulos sejam congruentes para que os triângulos sejam semelhantes. Eles construíram uma ampliação/redução a partir de dois ângulos congruentes aos do molde e verificaram que essa realmente era semelhante.
O segundo caso diz que basta que os lados sejam proporcionais. Eles construíram um triângulo a partir de três lados proporcionais e verificaram que ele realmente era semelhante ao molde.
O terceiro caso diz que basta que dois lados sejam proporcionais e o ângulo entre eles seja congruente ao seu correspondente no molde. Eles construíram um triângulo a partir de dois lados proporcionais e um ângulo entre eles congruente ao seu correspondente e verificaram que esse era realmente semelhante ao molde.
Concluímos, então, que os três casos de semelhança realmente garantem a semelhança de dois triângulos, sem a necessidade da medida de todos os lados e ângulos. O objetivo é que eles aprofundem o conceito de semelhança de triângulos e conheçam bem os casos para que possam, em um segundo momento, usá-los em exercícios, demonstrações e argumentações.
Propósito: Organizar as idéias estudadas na aula.
Atividade de Verificação
Tempo sugerido: 7 minutos.
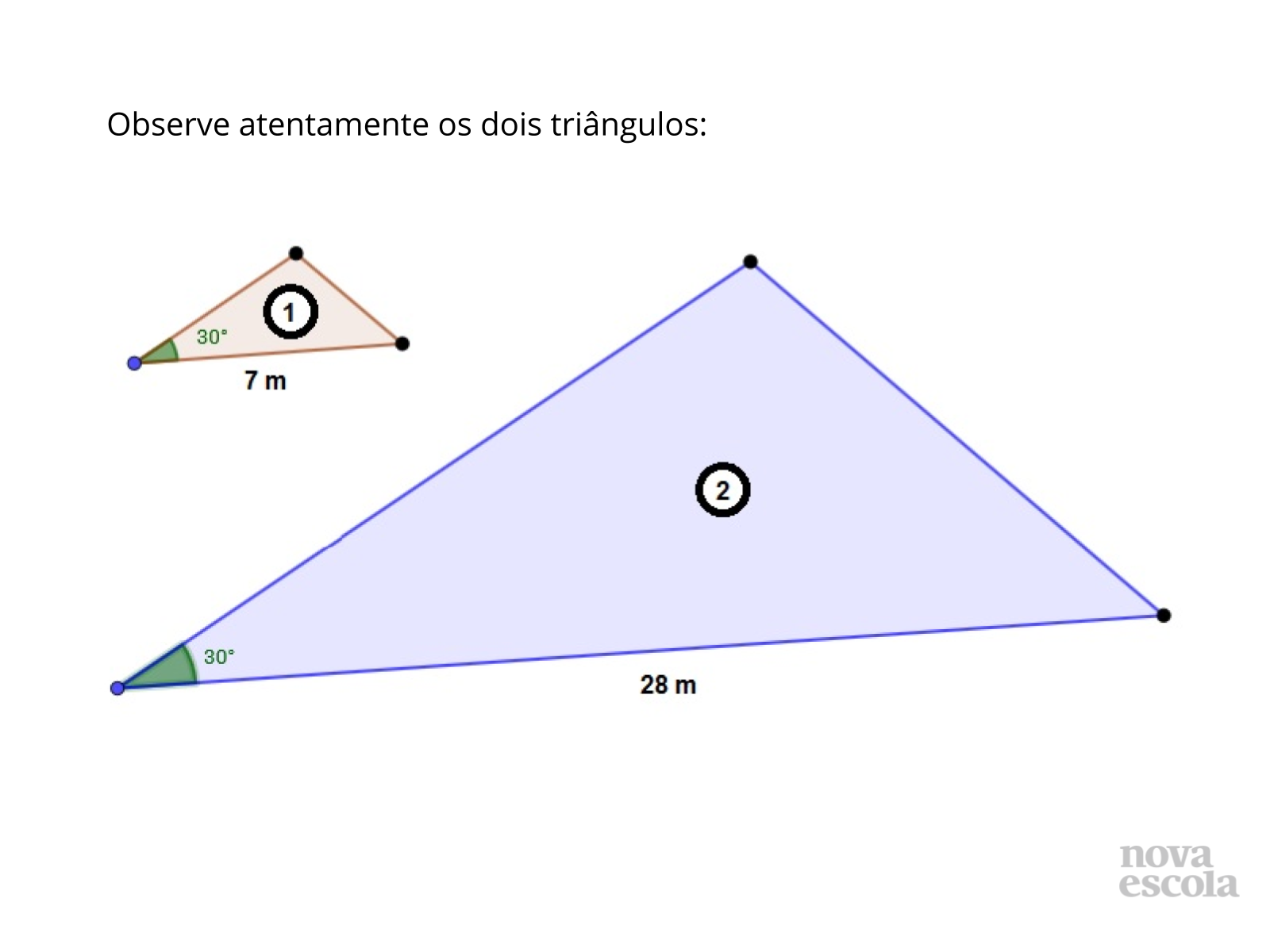
Orientação: São apresentados dois triângulos que possuem um ângulo congruente (30º) e cuja medida da base de um é quatro vezes a medida da base o outro. Essas duas informações não são suficientes para concluir que os dois triângulos são semelhantes. O objetivo é fazer com que os alunos reflitam sobre as condições necessárias para garantir a semelhança de dois triângulos.
Propósito: Verificar a compreensão dos alunos com relação aos temas estudados na aula.
Discuta com a turma:
- O fato deles parecerem semelhantes não é considerado importante na Matemática. São necessárias informações mais precisas.
Atividade Raio X para impressão: https://goo.gl/SH67LB
Resolução da Atividade Raio X: https://goo.gl/GUCsUS
Atividades Complementares: https://goo.gl/mVuaZc
Resolução das Atividades Complementares: https://goo.gl/ZpYKQs
Raio X

Tempo sugerido: 7 minutos.
Orientação: Essa atividade introduz ao aluno o que seria uma demonstração matemática. Assim sendo, você deve orientá-los a usar apenas as informações que foram dadas. Em uma demonstração, não podemos fazer nenhuma suposição que não seja baseada em dados. Eles também devem tomar cuidado com a linguagem.
Antes da resolução, você pode retomar com a sala alguns conceitos estudados: congruência, proporção, lados correspondentes, semelhança.
Queremos saber se os alunos entenderam quais são as condições necessárias para que dois triângulos sejam semelhantes. A primeira informação (ambos têm um lado congruente de 30º) não garante a semelhança, pelo primeiro caso são necessários dois ângulos congruentes. A segunda informação (a base de um mede o dobro da base do outro) também não garante a semelhança. Todos os lados deveriam ser proporcionais (no caso, todos deveriam medir o dobro). Se considerarmos as duas informações, também não garantimos a semelhança. Sabemos que ambos têm um ângulo congruente e a base de um mede o dobro da base do outro.
Para resolver a atividade não é necessário conhecer os dados do triângulos em questão. A discussão é sobre as condições para que haja a semelhança. Essa ideia pode ser complexa para um aluno de 6º ano. Ele pode dizer que não dá pra resolver porque eu não sabe tudo. Mostre que essa resposta já é uma parte da solução. Ele já começou a resolver o problema.
Eles não farão nenhuma conta. A idéia de que um problema matemático que não tem nenhum cálculo pode ser meio chocante para os alunos.
Discuta com a Turma:
- A informação de Mariana prova que os dois triângulos são semelhantes? Se não, o que falta saber?
- A informação de Maria prova que os dois triângulos são semelhantes? Se não, o que falta saber?
- Se juntarmos as duas informações, isso prova que os dois triângulos são semelhantes? Se não, o que falta saber?
Propósito: Verificar a compreensão dos alunos com relação aos temas estudados na aula.
Materiais complementares para impressão:
Sugestão de adaptação para ensino remoto
Código do plano
MAT6_16GEO02
Recursos
- Necessários: Papel, lápis, caderno
- Opcionais: Meet, Zoom, WhatsApp, régua, tesoura, papel
Para este plano, foque na etapa: Atividade Principal
Aquecimento
Você pode disponibilizar aos alunos (via WhatsApp) o slide do Aquecimento que é uma preparação para Atividade Principal.
Atividade principal
Você pode propor uma aula invertida. Ou seja, você disponibiliza para os alunos os slides da “Atividade Principal” (2 a 5). Com o triângulo construído e no dia da aula marcado com eles, ouçam quais o retorno dos alunos quanto às atividades, possíveis dúvidas, equívocos e conclusões. A partir delas, você pode dar início e vivenciar conjuntamente, pelo meio de comunicação combinado (Meet, Hangout, Zoom) cada parte da atividade. Lembre se de retomar as ideias compartilhadas e vivenciadas pelos alunos. Compartilhe a tela e converse sobre o primeiro caso de congruência (AA) e faça do “Discuta com a turma” e assim sucessivamente. Partir das aprendizagens que eles tiveram em casa e valorizar para o início da sua aula, faz toda a diferença. Use a “Discussão das soluções” para saber se algum aluno pensou daquela maneira.
Se sua aula fora assíncrona, você pode deixar a atividade impressa na escola ou enviar pelo grupo de WhatsApp e combinar um retorno com eles para uma devolutiva. Nesse retorno, você pode enviar um áudio explicando as principais ideias da atividade e seu propósito. Ao final, os alunos registram na própria atividade suas conclusões. Caso eles tenham alguma dúvida, enviam pelo WhatsApp para que seja sanada pelo professor.
Encerramento
Inclua para finalizar a aula.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos podem estar ocupados com outras funções em casa ou mesmo trabalhando.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Paula Vieira Soares
Mentora: Renata S. Gonçalves
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
EF06MA20 - Construção de figuras semelhantes: ampliação e redução de figuras planas em malhas quadriculadas.
Objetivos específicos
Verificar os casos de semelhança de triângulos, através do estudo de ampliações e reduções.
Conceito-chave
Semelhança de Triângulos
Recursos necessários
- Régua;
- Papel sulfite;
- Tesoura
- Varetas (para construir pipas) - pode ser usado palito de churrasco, canudos, mas quanto mais fino o material, maior a precisão da construção dos alunos.
- Papel cartão ou cartolina.
Sugestões de Leitura
FERREIRA, Anna Rachel. O desafio de organizar e mediar o trabalho em grupo. Nova Escola: Prática Pedagógica, 19 de Abril. 2017 - Disponível em: https://goo.gl/dAQqbP (visitado em 02/12/2017)
MACHADO, Nílson José. Semelhança não é mera coincidência - (Coleção Vivendo a Matemática). Scipione, 2000.
BOALER, Jo. Mentalidades Matemáticas. 1ª ed. Porto Alegre - RS. Penso, 2018
DOLCE, Osvaldo. POMPEO, José Nicolau. Fundamentos da Matemática. Volume 9 - Geometria Plana. São Paulo - SP. Atual, 2005.
Conhecimentos que a turma deve dominar:
- Noção de semelhança de polígonos.











