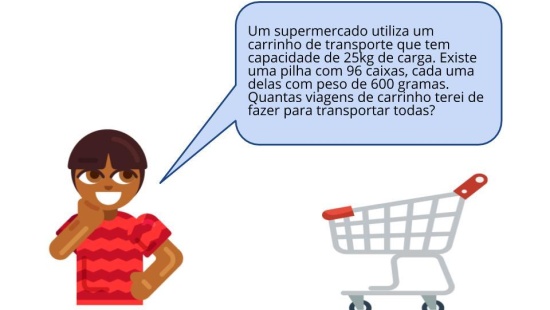
Aquecimento
Plano de Aula
Plano de aula: Metro quadrado e cúbico com Material Dourado.
Plano 2 de uma sequência de 10 planos. Veja todos os planos sobre Resolução de problemas de medidas envolvendo grandezas
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Dariel Barbosa de Melo Jr.
Mentor: Maria Aparecida Nemet Nascimento
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF06MA22) Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.
Objetivos específicos
- Identificar metro quadrado e metro cúbico, aplicar os conceitos de área e volume em situações lúdicas.
Conceito-chave
Medidas de área e volume padronizadas.
Recursos necessários
- Material dourado;
- Papel quadriculado 1 cm x 1 cm;
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
- Identificar metro quadrado e metro cúbico, aplicar os conceitos de área e volume em situações lúdicas.
Resumo da aula
 Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivos

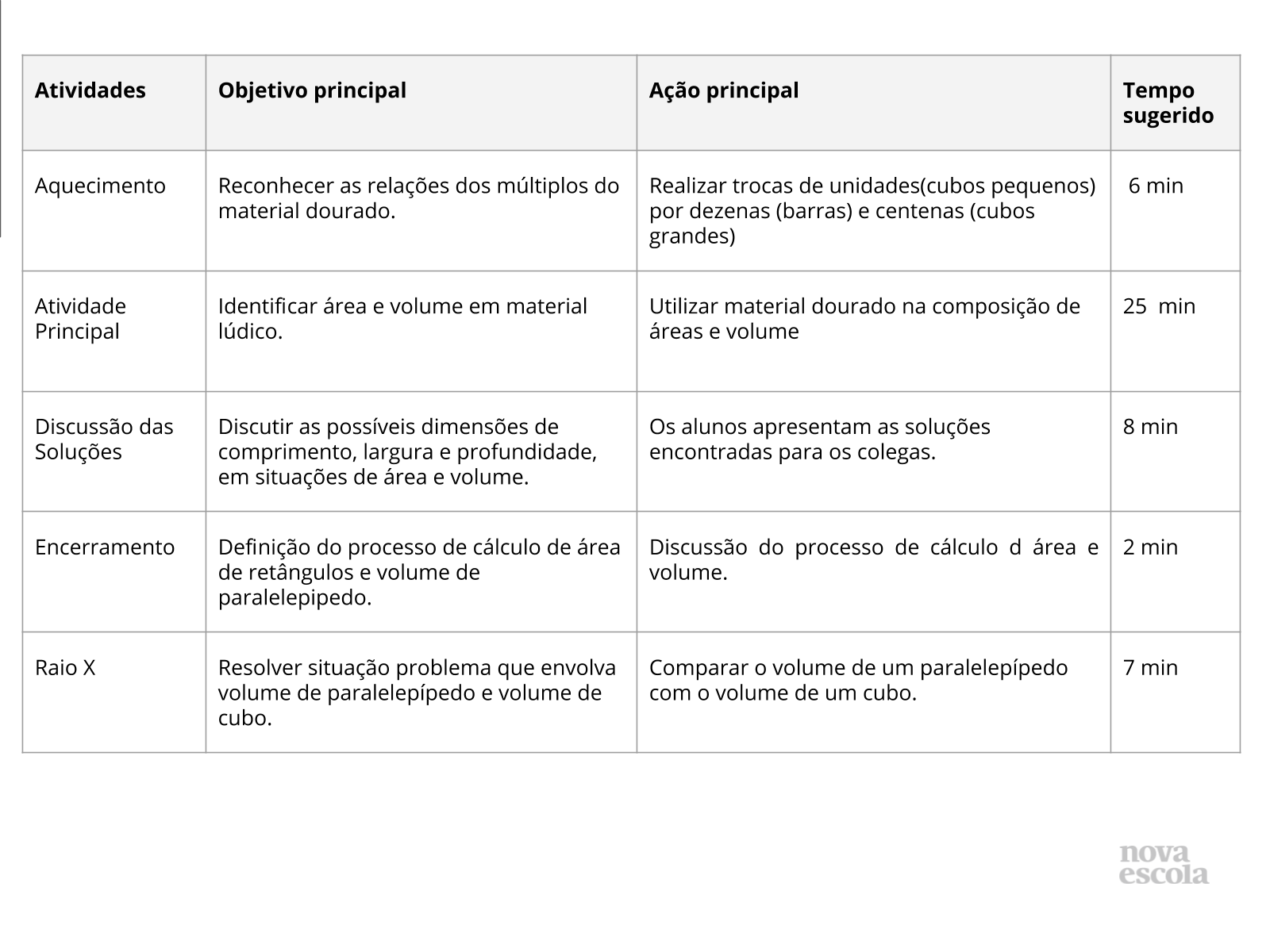
Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento (introdução).
 Aquecimento (introdução).
Aquecimento (introdução). Tempo sugerido: 5 minutos.
Orientação: Entregue a cada grupo de alunos um kit de material dourado, ou uma parte do kit, com no mínimo uma placa subdividida em 100 unidades, 10 barras subdivididas em 10 unidades e 20 cubos pequenos e unitários.
Os alunos devem formar números com o material dourado, de forma a reconhecer as trocas de 10 cubos pequenos e unitários por uma barra subdivididas em 10 unidades e 10 barras por uma placa subdividida em 100 unidades, onde:
1 cubinho representa 1 unidade;
1 barra equivale a 10 cubinhos (1 dezena ou 10 unidades);
1 placa equivale a 10 barras ou 100 cubinhos (1 centena, 10 dezenas ou 100 unidades);
1 cubo grande equivale a 10 placas ou 100 barras ou ainda, 1000 cubinhos (1 unidade de milhar,10 centenas, 100 dezenas ou 1000 unidades).
Propósito:Reconhecer a formação das classes e ordens dos números com o uso do material dourado.
Materiais complementares para impressão:
Aquecimento.
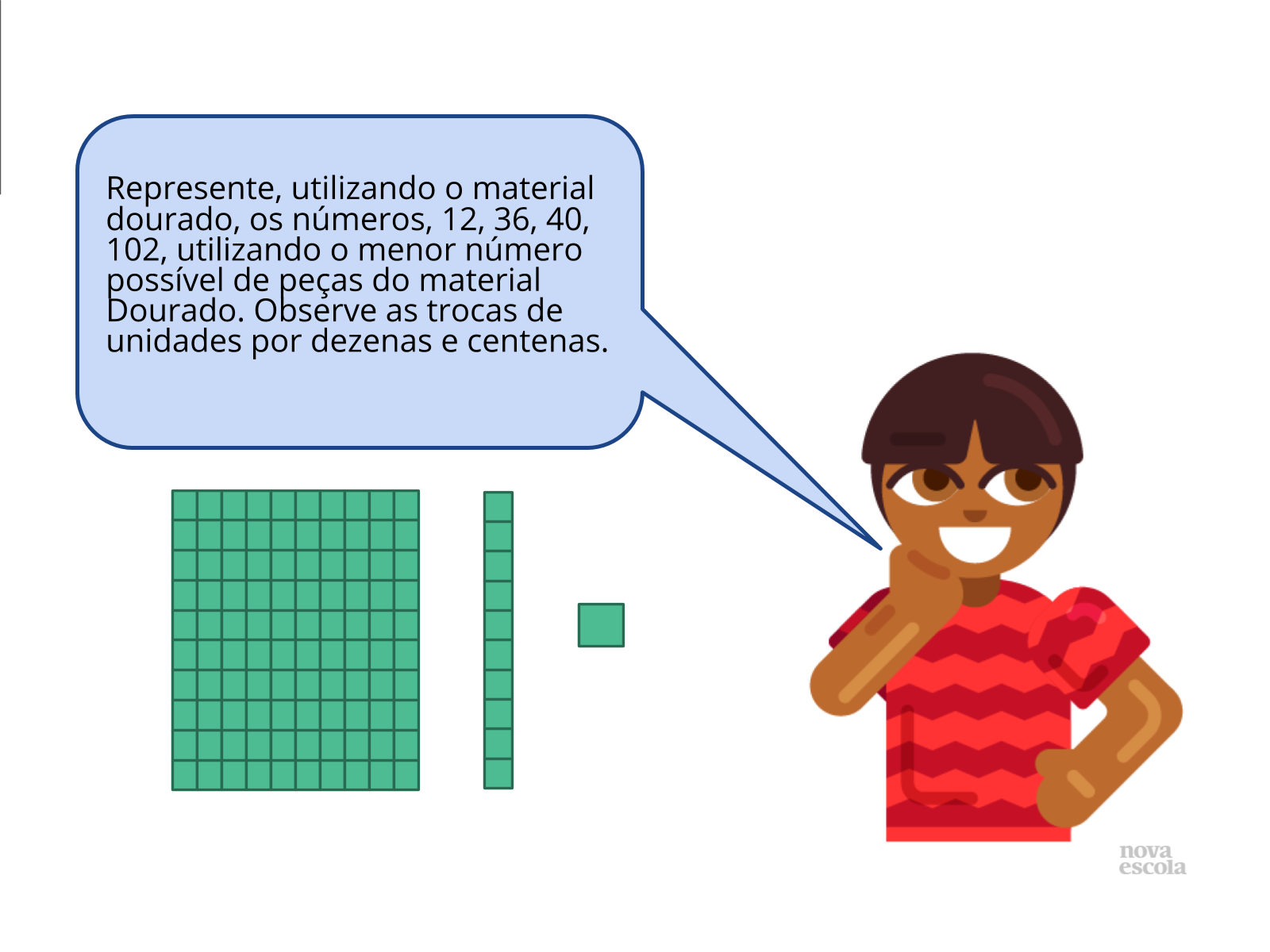 Aquecimento.
Aquecimento. Tempo sugerido: 5 minutos.
Orientação: Entregue a cada grupo de alunos um kit de material dourado, ou uma parte do kit, com no mínimo uma placa subdividida em 100 unidades, 10 barras subdivididas em 10 unidades e 20 cubos pequenos e unitários.
Os alunos devem formar números com o material dourado, de forma a reconhecer as trocas de 10 cubos pequenos e unitários por uma barra subdivididas em 10 unidades e 10 barras por uma placa subdividida em 100 unidades, onde:
1 cubinho representa 1 unidade;
1 barra equivale a 10 cubinhos equivalem (1 dezena ou 10 unidades);
1 placa equivale a 10 barras ou 100 cubinhos (1 centena, 10 dezenas ou 100 unidades);
1 cubo grande equivale a 10 placas 1000 ou 100 barras ou 1000 cubinhos (1 unidade de milhar,10 centenas, 100 dezenas ou 1000 unidades).
Propósito:Ambientar os alunos à utilização do material dourado e a compreender as características do sistema decimal: fazer agrupamentos de 10 em 10; fazer reagrupamentos; fazer trocas; estimular o cálculo mental.
Atividade principal (introdução)
 Atividade principal (introdução)
Atividade principal (introdução) Tempo sugerido: 25 minutos.
Orientação :Para essa atividade, utilizaremos uma sequência de procedimentos utilizando o material dourado e folhas de papel quadriculado. Os alunos devem ser orientados a observar outros processos de cálculo, além do processo lúdico, com a montagem de retângulos e paralelepípedos.
Materiais necessários:
- Kits de material dourado;
- Folhas de papel quadriculado de 1cm por 1 cm.
Propósito: Organizar, orientar os grupos, distribuir as comandas das atividades e os materiais necessários.
Materiais complementares para impressão:
Atividade Principal (Sequência 1).
 Atividade Principal (Sequência 1).
Atividade Principal (Sequência 1). Tempo sugerido: 25 minutos.
Orientação a): Entregue o número exato de barras para que os alunos montem os retângulos, de forma que sintam a necessidade da troca de barras das dezenas por unidades, para a realização completa da atividade.
Relembre aos alunos que perímetro é a soma das medidas dos lados e que, a partir das possíveis medidas dos lados, deve-se escolher aquela que apresenta menor soma.
1 e 70
2 e 35
5 e 14
7 e 10
Orientação b): Da mesma forma que a atividade anterior, entregue o número exato de cubos, para que os alunos, após as trocas, montem um retângulo de lados iguais (quadrado). Observar que neste caso, não existem diferentes medidas de comprimento e largura.
Vocabulário: Professor, nesse momento explique aos alunos que um retângulo é um quadrilátero que possui todos os ângulos internos congruentes. O quadrado é um caso particular de um retângulo em que todos os lados têm o mesmo comprimento.
Discuta: Como o cálculo de área pode ser feito sem o material dourado ou a folha quadriculada?
Propósito: Reconhecer o cálculo da área de figuras retangulares através do produto do comprimento pela largura (ou da base pela altura).
Atividade Principal
 Atividade Principal
Atividade Principal Sequência 2
Tempo sugerido: 25 minutos.
Orientação: Da mesma forma que a sequência 1, os alunos vão utilizar o papel quadriculado e determinar as possíveis medidas dos lados dos retângulos.
Discuta com a turma:
Como o cálculo de área pode ser feito sem o material dourado ou a folha quadriculada?
Propósito: Reconhecer o cálculo da área de figuras retangulares através do produto do comprimento pela largura (ou da base pela altura).
Atividade Principal - Sequência 3
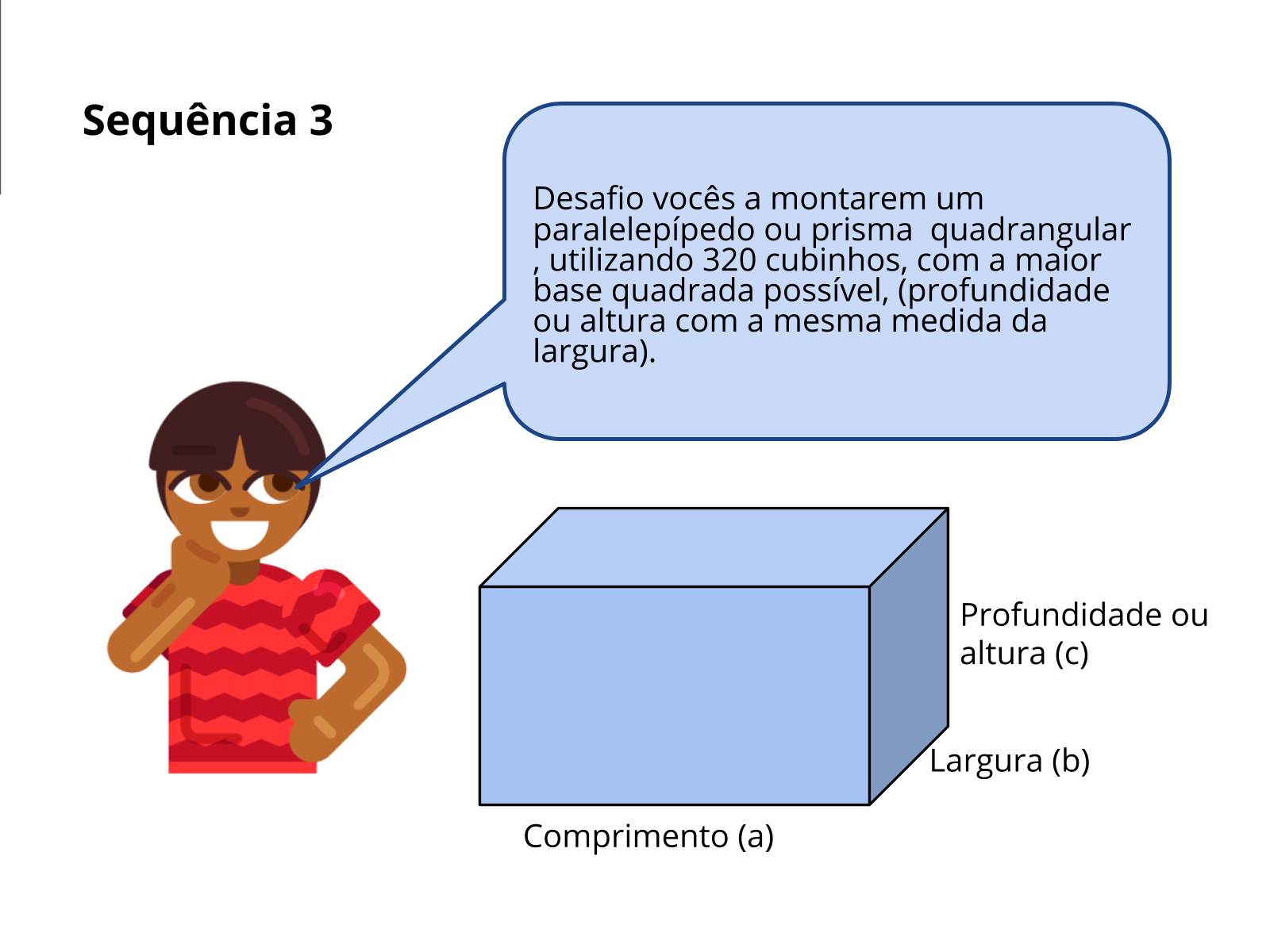
Tempo sugerido: 25 minutos.
Orientação: Oriente os alunos sobre as possíveis medidas de comprimento, largura e profundidade que, a partir de suas multiplicações, têm 320 como produto. A seguir, eles devem verificar quais resultados têm a largura e profundidade ( altura) com a mesma medida, para formar as bases quadradas.
Vocabulário: É importante ressaltar que os chamados “prismas regulares” são aqueles cujas bases são polígonos regulares e, portanto, formados por prismas retos e que, se todas as faces do prisma forem quadrados, trata-se de um cubo; e, se todas as faces são paralelogramos, o prisma é um paralelepípedo.
Discuta: Como o cálculo do volume pode ser feito sem o material dourado ?
Professor, enfatize para os alunos que um prisma é um poliedro que possui uma base inferior e uma base superior. Essas bases são paralelas e congruentes, isto é, possuem as mesmas formas e dimensões, e não se interceptam. Para determinarmos o volume de um prisma qualquer, nós calculamos a área de sua base para, em seguida, multiplicá-la pela sua altura. Sendo assim:
V = (área da base) . altura
Na imagem acima, a área do prisma de base quadrada pode ser calculada por:
V = a . b . c ou Volume = comprimento x largura x altura
Propósito: Reconhecer o cálculo do volume do paralelepípedo através do produto do comprimento pela largura pela profundidade.
Atividade alternativa - Sequência 3 A: (Caso o professor não tenha acesso ao kit de material dourado).
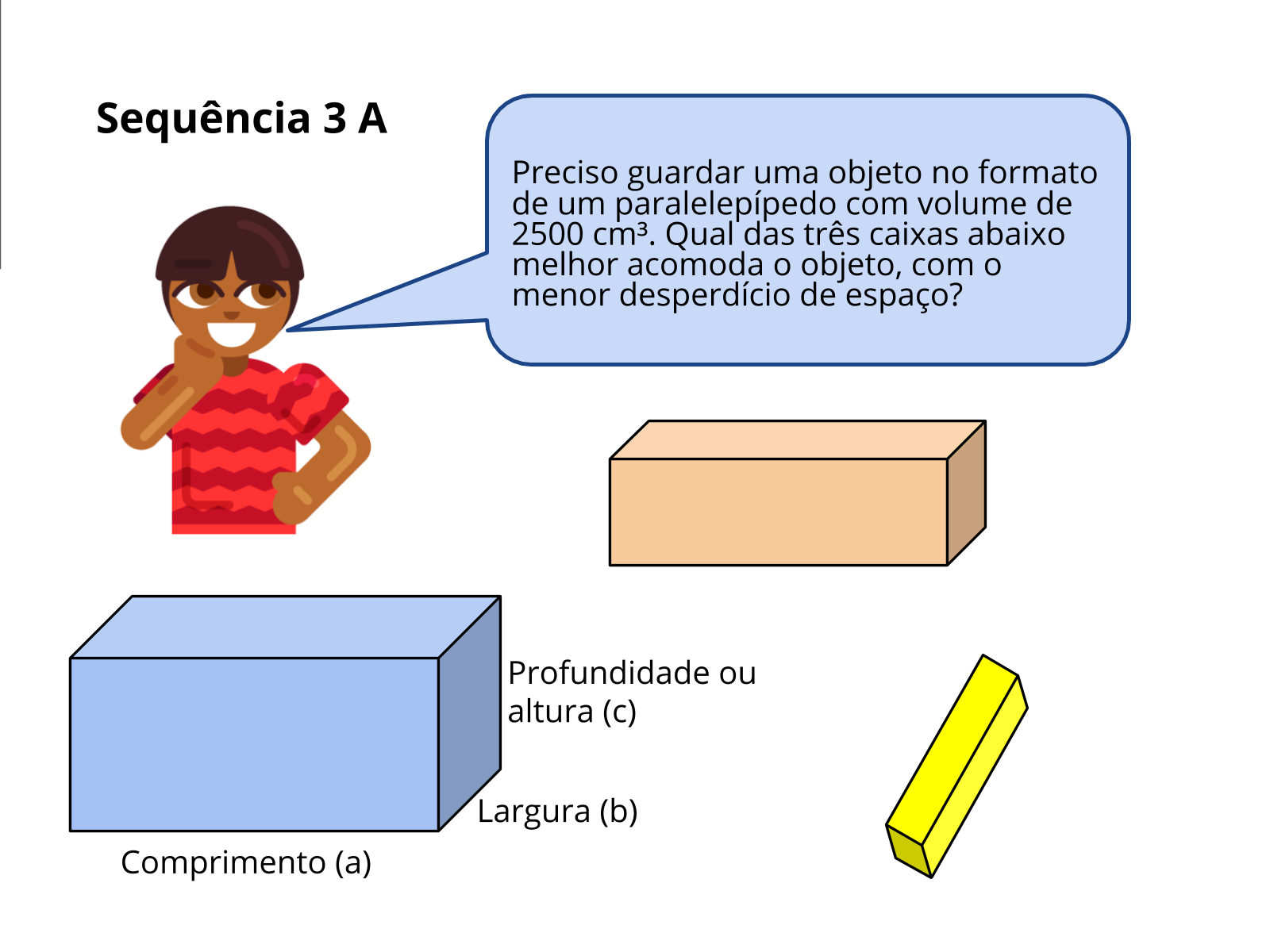 Atividade alternativa - Sequência 3 A: (Caso o professor não tenha acesso ao kit de material dourado).
Atividade alternativa - Sequência 3 A: (Caso o professor não tenha acesso ao kit de material dourado). Tempo sugerido: 10 minutos.
Orientação: Entregue aos alunos 3 caixas de diferentes tamanhos porém, devem ser previamente medidas pelo professor (comprimento, largura e profundidade ou altura).
Exemplo: Uma caixa de sapato, tamanho adulto, em geral costumam medir 30 cm x 20 cm x 10 cm; uma caixa de sapatos tamanho infantil, que de modo geral costumam medir 18 cm x 15 cm x 10 cm e uma caixa de creme dental de 10cm x 3cm x 2cm (tamanho médio).
Solicite aos alunos que determinem, através de cálculos, qual das caixas é mais adequada para guardar o objeto no formato de paralelepípedo com volume de 2500 cm³, considerando o menor desperdício de espaço possível.
Vocabulário: Professor, é importante ressaltar que os chamados “prismas regulares” são aqueles cujas bases são polígonos regulares e, portanto, formados por prismas retos e que, se todas as faces do prisma forem quadrados, trata-se de um cubo; e, se todas as faces são paralelogramos, o prisma é um paralelepípedo.
Discuta com a turma: Qual a melhor estratégia para determinar o volume das caixas?
Enfatize para os alunos que um prisma é um poliedro que possui uma base inferior e uma base superior. Essas bases são paralelas e congruentes, isto é, possuem as mesmas formas e dimensões, e não se interceptam. Para determinarmos o volume de um prisma qualquer, nós calculamos a área de sua base para, em seguida, multiplicá-la pela sua altura. Sendo assim:
V = (área da base) . altura
Na imagem acima, a área do prisma de base quadrada pode ser calculada por:
V = a . b . c ou Volume = comprimento x largura x altura
Propósito: Reconhecer o cálculo do volume do paralelepípedo através do produto entre as medidas de comprimento, largura e profundidade (altura).
Discussão da solução.
 Discussão da solução.
Discussão da solução. Tempo sugerido: 8 minutos.
Orientação: Proponha aos alunos que compartilhem com a turma os resultados encontrados nas atividades.
Discuta: Como o cálculo do volume pode ser feito sem o material dourado ? Qual foi a dificuldade nas montagens de área e volume com o material dourado?
Propósito: Reconhecer que o cálculo da área e do volume podem ser obtidos de formas alternativas por meio do material dourado, sem necessariamente se pautar na utilização de fórmulas.
Encerramento
 Encerramento
Encerramento Tempo sugerido: 2 minutos.
Propósito: Relembrar os temas trabalhados nesta aula (diferenciar o cálculo da área do cálculo de volume).
Raio x

Tempo sugerido: 8 minutos.
Orientação ao professor: Indicar o cálculo do volume através do produto de comprimento, largura e profundidade, retomando o que foi observado na atividade com o material dourado, no caso das medidas dos cubos, é importante destacar que as dimensões comprimento, largura e profundidade( altura) têm a mesma medida, e são conhecidas por arestas, sendo o volume do cubo o valor da aresta “elevado ao cubo” ( V = a³).
Discuta com a turma: Além de obter o volume, através do produto das três dimensões, poderíamos realizar o cálculo da área da base e multiplicar pela altura do paralelepípedo, ou seja: V = a . b . c ou Volume = comprimento x largura x altura
Materiais complementares para impressão:
Sugestão de adaptaçãopara ensino remoto
Código do plano
MAT6_19GRMO02
Recursos
- Necessários: Folha sulfite, lápis, caderno, malha quadriculada
- Opcionais: Meet, Zoom, WhatsApp
Decomposição de formas para calcular área: https://www.youtube.com/watch?v=vCAlSuVaxB4
Fórmula da área: https://www.youtube.com/watch?v=2-DjxtX-NvM
Para este plano, foque na etapa: Atividade Principal
Atividade Principal (adaptada)
Você pode fazer uma sala de aula invertida. Vale ressaltar que nessa aula é essencial o uso da malha quadriculada. Envie com antecedência as seguintes orientações aos alunos:
a) Separe uma malha quadriculada (caso não tenha, você pode imprimir ou desenhar)
b) Desenhe na malha retângulos com:
- Área de 70u² com a menor medida possível do perímetro.
- Área de 49u² com medidas iguais de comprimento e largura.
- Área de 50u² com a medida do comprimento valendo o dobro da medida da largura.
- Área de 81u² com lados de mesma medida.
Considere cada quadrado da malha, uma unidade de medida (u²). Sugerimos que envie junto com as orientações um áudio e/ou vídeo orientativo. Mantenha um canal de comunicação para dúvidas e esclarecimentos antes do encontro combinado. No dia do encontro marcado (Meet, Hangouts, Zoom, Teams), deixe que os alunos compartilhem seus desenhos. É importante o planejamento da aula. Se não surgirem respostas diferentes pelos registros dos alunos, como desenhar o retângulo de 70u² com e menor medida possível do perímetro, é necessário que você tenha desenhado todas as possíveis soluções para que seja discutido nesse momento. Instigue os alunos a pensar sobre essas possibilidades. Discuta comprimento, largura e cálculo de área. Veja se eles compreendem o cálculo da área como base x altura ou se algum aluno levanta a hipótese de contar o número de quadradinhos. Se sua aula fora assíncrona, deixe a tarefa na escola ou envie pelo WhatsApp. Grave um áudio explicando e peçam que enviem para você combinando um retorno de devolutiva. Nesse retorno, você pode enviar o print com registros dos outros alunos para que eles comparem com suas estratégias e colem no seu caderno como repertório de soluções.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Dariel Barbosa de Melo Jr.
Mentor: Maria Aparecida Nemet Nascimento
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF06MA22) Reconhecer que o resultado de uma medida depende da unidade de medida utilizada.
Objetivos específicos
- Identificar metro quadrado e metro cúbico, aplicar os conceitos de área e volume em situações lúdicas.
Conceito-chave
Medidas de área e volume padronizadas.
Recursos necessários
- Material dourado;
- Papel quadriculado 1 cm x 1 cm;
- Atividades impressas em folhas, coladas no caderno ou não.