Resumo da aula
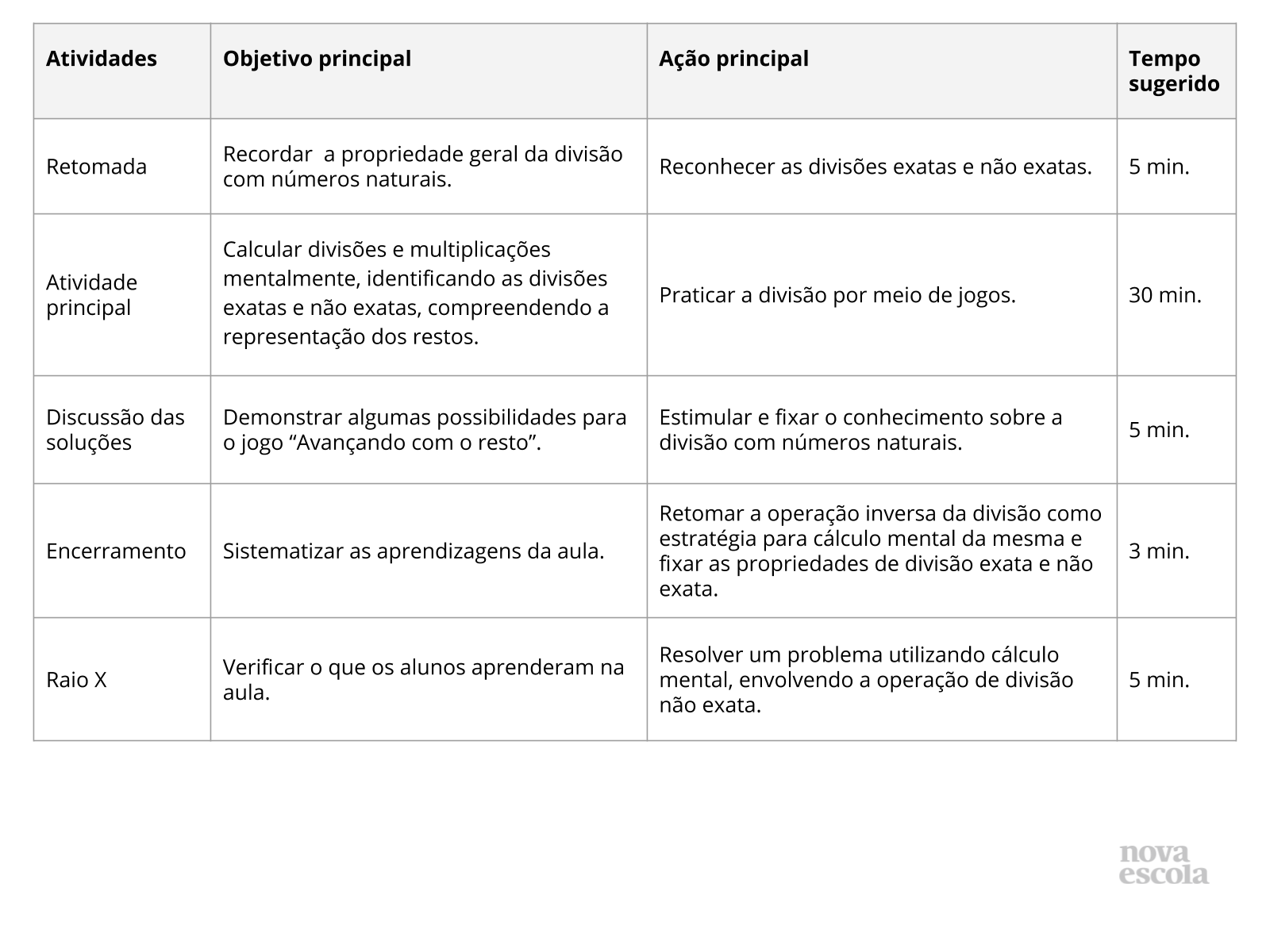
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete no quadro ou leia o objetivo da aula para os alunos.
Propósito: Compartilhar o objetivo da aula com os alunos.
Retomada

Tempo sugerido: 5 minutos
Orientações: Estimular os alunos a responderem as perguntas para recordarem os termos fundamentais das divisões exatas e não exatas. E relembrar que realizando a multiplicação (operação inversa) entre o quociente e divisor e somando-se ao resto obtém-se o dividendo, verificando assim se a operação está correta.
Propósito: Relembrar o conceito de divisões exatas e não exatas enfatizando o resto.
Discuta com a turma:
- Vocês conseguem resolver o problema proposto por Roberta, mentalmente?
- O que Cauê quer dizer ao perguntar como podemos comprovar a divisão?
- Faltava quanto para que a divisão fosse exata? Por quê?
- Se estávamos dividindo entre seis amigos, quais as possibilidades de resto para a divisão ser inexata?
- O que significa uma divisão inexata?
Atividade Principal

Tempo sugerido: 30 minutos.
Orientações: Esclarecer as regras do jogo aos alunos. Explicar que o grupo (dois alunos) deve calcular os resultados das divisões mentalmente e atentar-se ao resto, pois este valor corresponde ao número de casas que irá movimentar no tabuleiro.
Propósito: Apresentar as regras do jogo.
Discuta com a turma:
- Quais estratégias de cálculo mental vocês utilizarão para saber calcular o valor da divisão e descobrir o resto?
- No início do jogo é melhor obter restos menores ou maiores? Por quê?
Materiais complementares
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal

Tempo sugerido: 30 minutos.
Orientações: Esclarecer as regras do jogo aos alunos. Explicar que o grupo (dois alunos) deve calcular os resultados das divisões mentalmente e atentar-se ao resto, pois este valor corresponde ao número de casas que irá movimentar no tabuleiro.
Propósito: Apresentar as regras do jogo.
Discuta com a turma:
- Quais estratégias de cálculo mental vocês utilizarão para saber calcular o valor da divisão e descobrir o resto?
- No início do jogo é melhor obter restos menores ou maiores? Por quê?
Atividade Principal

Tempo sugerido: 30 minutos.
Orientações: Organizar a sala em grupos com duas equipes com o mesmo número de alunos cada. Por exemplo: um grupo com 4 alunos, deverão ser organizados em duas equipes de 2 alunos cada (2 alunos da equipe verde e 2 alunos da equipe vermelha), para disputarem o jogo de forma coletiva. Em seguida, distribuir um tabuleiro, dois dados e duas fichas (uma de cada cor) para cada duas equipes que disputarão o jogo. Mediar e orientar os alunos sobre as diversas possibilidades de estratégias para realizar o cálculo mental da divisão com resto. Recorde-os que os números do tabuleiro representam os dividendos e a soma dos números dos dados são os respectivos divisores, o resto da divisão, corresponde ao número de casas que deverão avançar com o marcador.
O jogo é uma adaptação do material disponibilizado no site: http://mathema.com.br/jogos-fundamental1/avancando-com-o-resto-2/
Propósito: Chegar em primeiro lugar na palavra FIM, onde avançarão com o valor do resto das divisões.
Discuta com a turma:
- Vocês aceitam o desafio desse jogo, que consiste em descobrir mentalmente o resto de uma divisão, para avançar no tabuleiro?
- Vamos descobrir as diferentes estratégias que cada grupo irá desenvolver para avançar na partida?
- Todos entenderam como procederá o jogo?
Discussão da solução
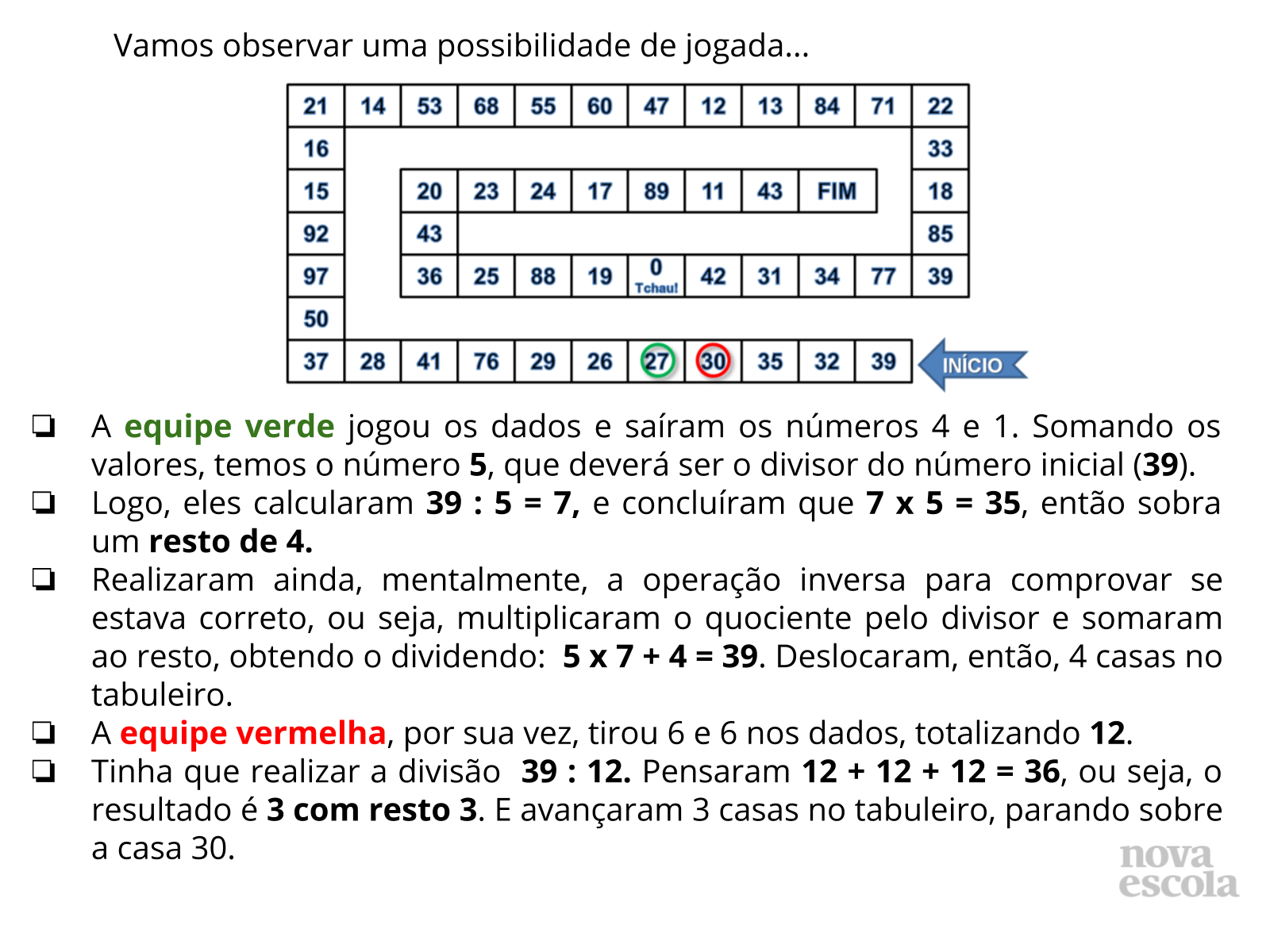
Tempo sugerido: 5 minutos.
Orientações: Explicar aos alunos as etapas do jogo, esclarecendo as estratégias que podem ser utilizadas para realizar os cálculos das divisões não exatas.
Propósito: Demonstrar e provocar a reflexão dos alunos sobre uma possibilidade de jogada e estratégia de cálculo mental.
Discuta com a turma:
- Como podemos determinar o resto das divisões, mentalmente?
- Como a operação inversa pode facilitar a determinação do resto da divisão?
Discussão da solução
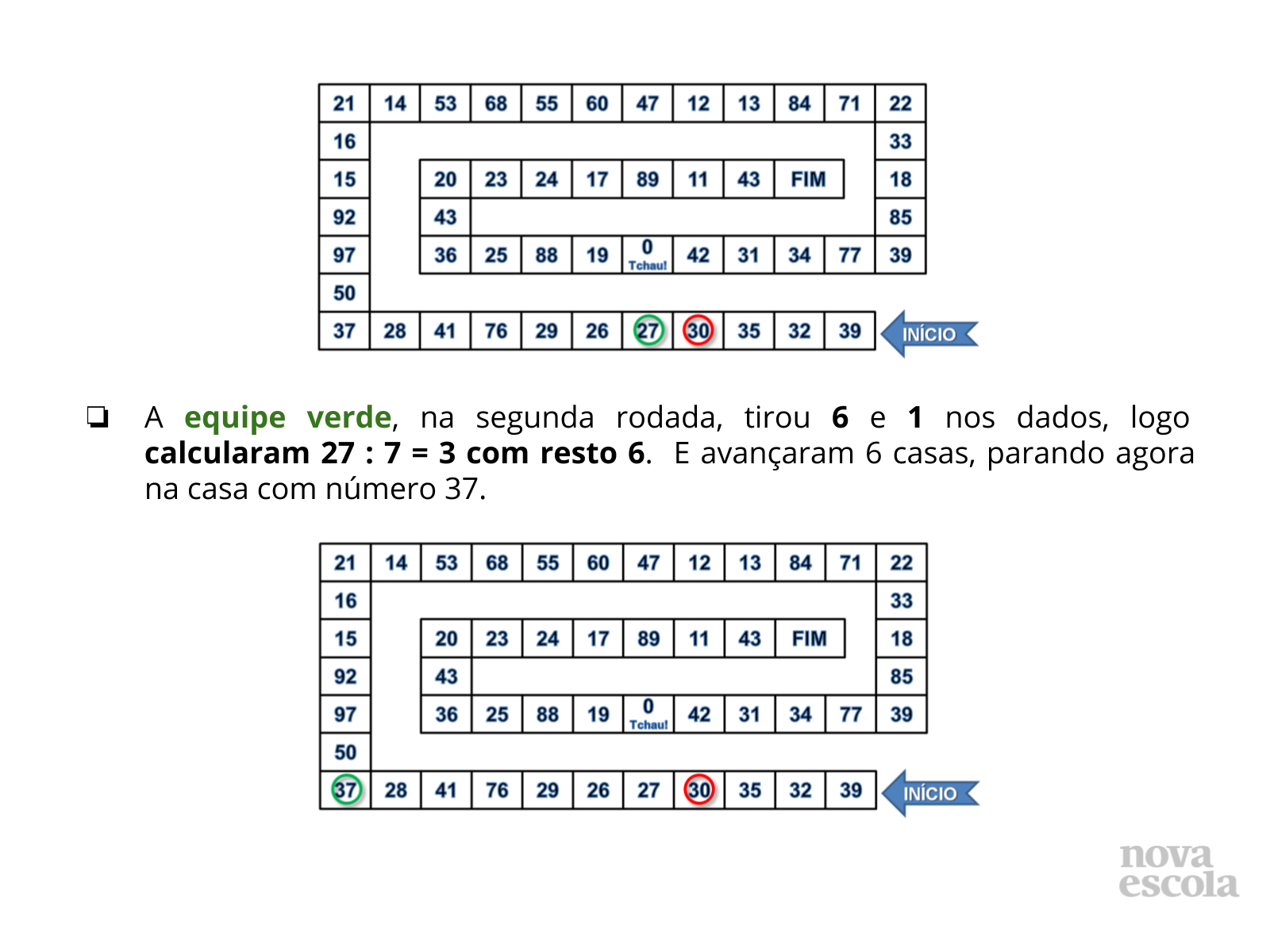
Tempo sugerido: 5 minutos.
Orientações: Explicar aos alunos as etapas do jogo, esclarecendo as estratégias que podem ser utilizadas para realizar os cálculos das divisões não exatas.
Propósito: Demonstrar e provocar a reflexão dos alunos sobre uma possibilidade de jogada e estratégia de cálculo mental.
Discuta com a turma:
- Como podemos determinar o resto das divisões, mentalmente?
- Quanto deve ser o divisor para a equipe vermelha passar a verde?
Encerramento

Tempo sugerido: 3 minutos.
Orientações: Encerre relembrando que a divisão é o inverso da multiplicação e aproveite a oportunidade para recordar a nomenclatura dos termos da divisão e a diferença da divisão exata da não exata. Demonstre que a operação inversa pode ser utilizada para tirar a prova real da divisão se for acrescentado o respectivo resto. E esta estratégia pode ser utilizada durante o jogo para facilitar o cálculo mental rapidamente. É importante recordar ainda que na divisão com números naturais o resto sempre será um número menor que o divisor.(por exemplo, uma divisão com divisor 6, o resto pode ser os números 0, 1, 2, 3, 4 ou 5 apenas).
Propósito: Compreender o conceito de divisão, identificando as exatas e as não exatas com seu respectivo resto. Como também relembrar a possibilidade de verificar se a divisão está correta, usando a operação inversa.
Discuta com a turma:
- Se o dividendo desse exemplo fosse 24, como ficaria a operação? Como a divisão seria denominada?
- Para obter a prova real da divisão devemos realizar a operação inversa, ou seja a multiplicação. Se for uma divisão não exata, como você realizará esse cálculo mentalmente?
- Por que é importante compreender esse conceito? Como essa estratégia pode nos auxiliar com as operações de divisão e multiplicação?
Raio X
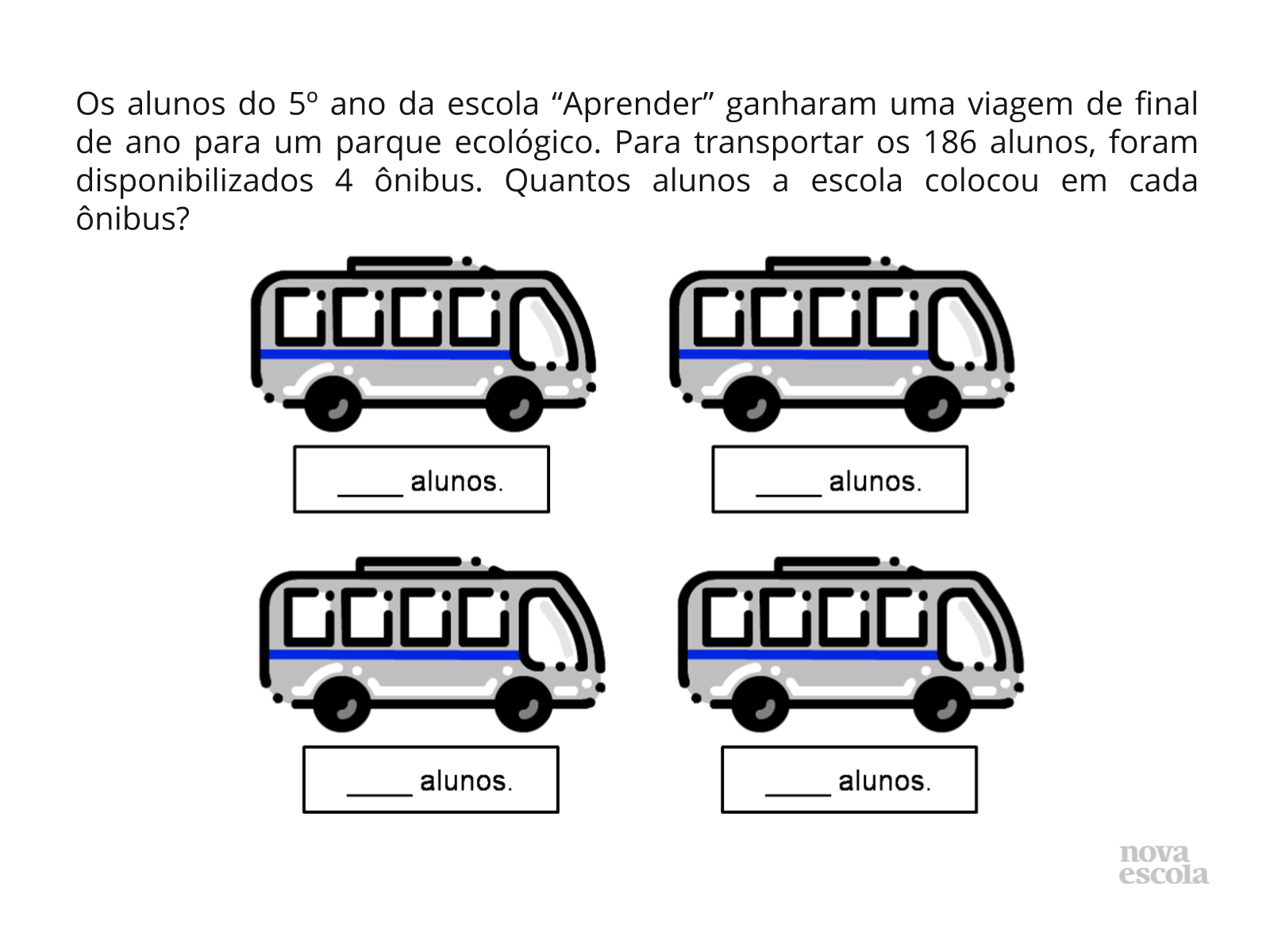
Tempo sugerido: 5 minutos
Orientações: Para finalizar a aula, apresente a atividade em que terão que resolver a divisão não exata.
Propósito: Avaliar se os alunos realizam o cálculo da divisão com resto em um contexto diferente do abordado no jogo.
Discuta com a turma:
- Qual operação você utilizará para resolver o problema? Por quê?
- Os quatro ônibus levarão a mesma quantidade de alunos cada um? Por quê?
Materiais complementares
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 


















