Objetivo
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Monica Dias do Nascimento
Mentor: Sônia Maria dos S. Campos Neves
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF05MA08) Resolver e elaborar problemas de multiplicação e divisão com números naturais envolvendo números racionais cuja representação decimal é finita (com multiplicador natural e divisor natural e diferente de zero), utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
Objetivos específicos
Resolver problemas que envolvem multiplicação de um número fracionário por um número inteiro.
Conceito-chave
Resolução da operação de multiplicação envolvendo frações e números inteiros.
Recursos necessários
- Lápis,
- lápis de cor,
- papel,
- borracha,
cópia das atividades.
Tempo sugerido: 2 minutos.
Orientação: Apresentar para os alunos o objetivo da aula.
Propósito: Deixar o aluno consciente do objetivo da aula, qual conceito será discutido e qual é o foco de aprendizagem.
Aquecimento
Tempo sugerido: 3 minutos.
Orientação: Resolver o problema coletivamente com a condução do professor, pois é através de questionamentos e sugestões de reflexões que serão expostos os conhecimentos prévios dos alunos e suas possíveis fragilidades. Dessa forma, trazer à tona discussões a respeito das estratégias possíveis para a resolução, qual(is) operação(ões) está(ão) envolvida(s) no problema, dentre outros aspectos que possam surgir.
Propósito: Nessa atividade a intenção é de identificar se os alunos estão apropriados do significado de um número fracionário, assim como o reconhecimento da fração como uma extensão dos números naturais.
Discuta com a turma:
- Qual é a pergunta do problema?
- Qual é a operação matemática que você pensou ser a mais adequada para resolver este problema? Poderia ser outra operação?
- Você sugere outra estratégia de resolução?
- E se o próximo que receber também comer apenas 3 pedaços, qual fração representa?
- Ambos comeram 3 pedaços, isso significa que comeram a mesma quantidade?
Atividade principal
Tempo sugerido: 17 minutos.
Orientação: Inicialmente, propor a leitura e a resolução do problema individualmente e em seguida, discutir com os colegas.
Propósito: Esta atividade espera identificar as diferentes estratégias que possam surgir como propostas dos alunos para a resolução do problema.
Discutir com a turma:
- O que significa cada essas fração? Como podemos representá-la?
- O que cada fração representa em relação ao todo?
- Existe mais de uma possibilidade de resposta para o problema? Justifique sua resposta.
- Qual(ais) é(são) o(s) principal(ais) comando(s) do problema?
Materiais complementares
Resolução da Atividade Complementar
Sugerimos como complementar a atividade publicada no link abaixo: https://novaescola.org.br/conteudo/6315/introducao-a-problemas-com-fracoes.
Discussão das soluções
Tempo sugerido: 12 minutos.
Observação: Discussão das diversas respostas que poderão surgir, a partir das quais o professor deverá provocar questionamentos e reflexões que levem os alunos a encontrar a solução do problema. É preciso destacar a importância de ressignificar o erro, caso ocorra durante a resolução.
Propósito: Realizar discussão a partir das respostas apresentadas pelos alunos.
Discutir com a turma:
- O que significa a parte pintada?
- O que significa o número fracionário (dois quintos)?
- Para dividir o todo, ou seja, as 100 unidades em cinco partes, devemos agrupar quantos quadradinhos?
- Por que devemos considerar duas das cinco partes pintadas de rosa?
- Por que na representação final, usamos 7 quadrinhos e não 21?
Discussão das soluções
Tempo sugerido: 12 minutos.
Observação: Discussão das diversas respostas que poderão surgir, a partir das quais o professor deverá provocar questionamentos e reflexões que levem os alunos a encontrar a solução do problema. É preciso destacar a importância de ressignificar o erro, caso ocorra durante a resolução.
Propósito: Realizar discussão a partir das respostas apresentadas pelos alunos.
Discutir com a turma:
- O que significa o número fracionário?
- Por que na representação final, usamos 7 quadrinhos e não 21?
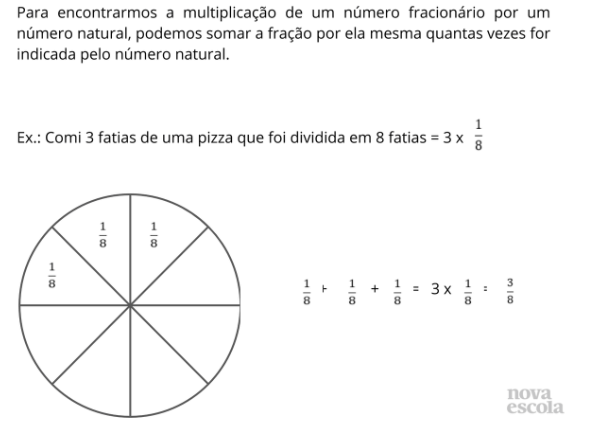
Sistematização do conceito
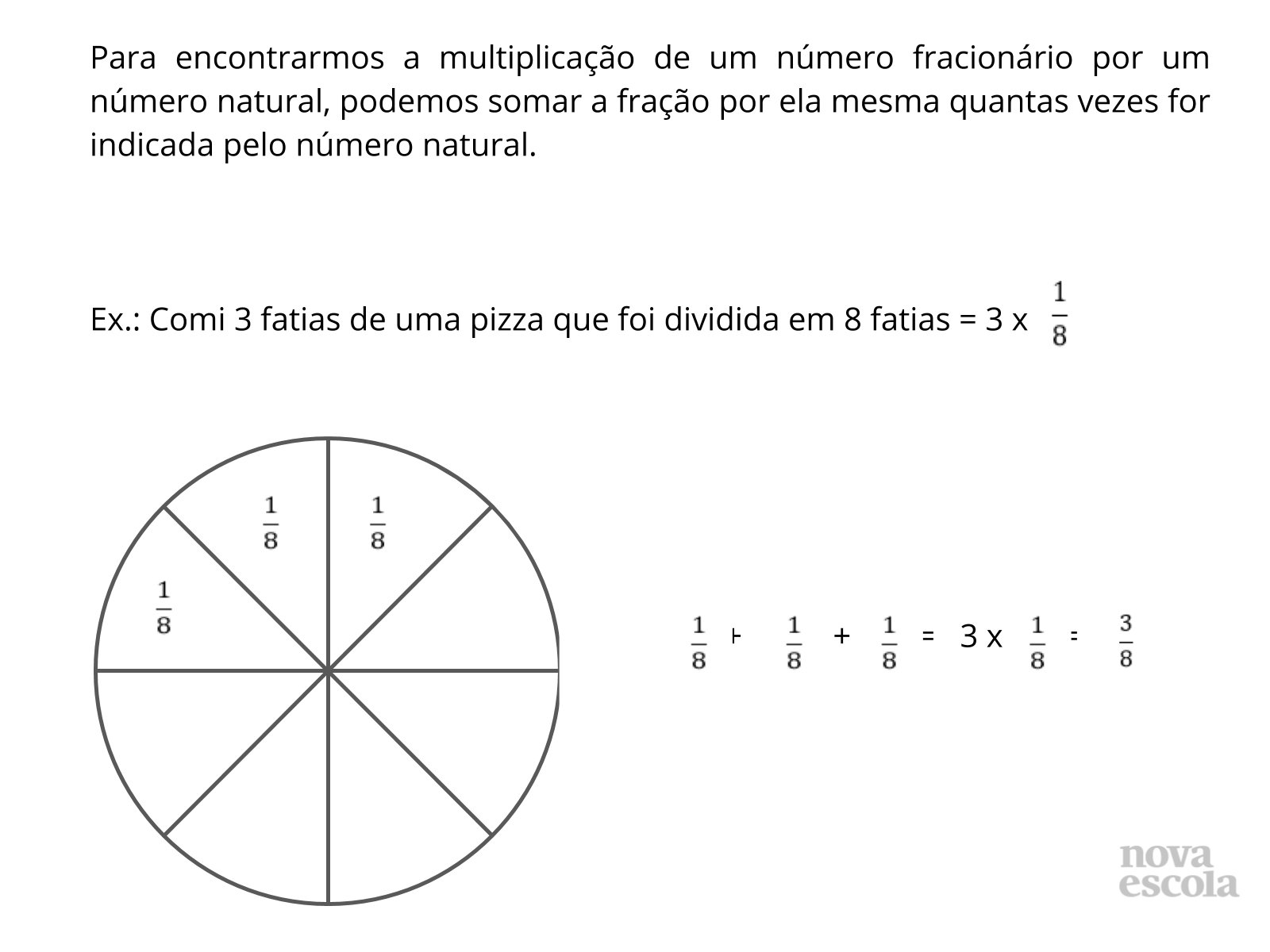
Tempo sugerido: 5 minutos.
Orientação: Propor ao aluno uma reflexão a partir das resoluções feitas ao longo da aula.
Propósito: A proposta deste momento da aula é organizar as ideias e conceitos para a resolver a multiplicação entre uma fração por um número inteiro.
Discuta com a turma:
- Qual é a principal operação proposta no problema?
- Por que representar a adição de parcelas iguais através da multiplicação?
- A fração que representa a resposta da pergunta deveria ser 3/24?
Encerramento
Tempo sugerido: 5 minutos.
Orientação: Elaborar, coletivamente, uma síntese das principais ideias e conceitos discutidos ao longo da aula, além de realizar a leitura do já apresentado.
Propósito: Explorar a aprendizagem construída na aula.
Discuta com a turma:
- Por que na adição de frações a soma é feita entre os numeradores e o denominador é repetido?
- Qual é o significado do número inteiro no problema?
Raio X
Tempo sugerido: 6 minutos.
Orientação: Observar a resolução apresentada pelos alunos, para identificar as dificuldades quanto a multiplicação entre uma fração e um número inteiro.
Propósito: Identificar o nível de compreensão do aluno acerca da temática discutida, assim como as possíveis fragilidades de compreensão.
Discuta com a turma:
- Qual a operação que você utilizou para responder o problema?
- Poderia ser outra operação? Qual?
- Artur respondeu que foram vendidas 3/21 de frutas. Você concorda?
Materiais complementares
