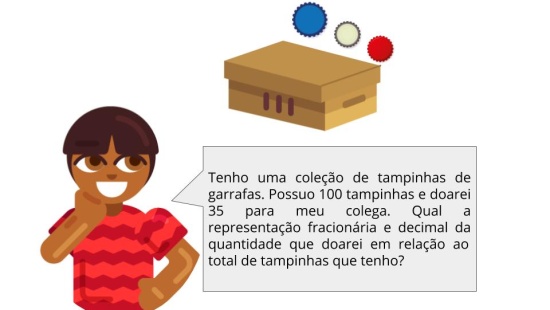
Atividade principal
Plano de Aula
Plano de aula: Representando frações
Plano 4 de uma sequência de 10 planos. Veja todos os planos sobre Números racionais nas suas formas fracionária e decimal
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Cátia do Vale dos Santos Mendes
Mentor: Sônia Maria dos Santos Campos Neves
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF05MA03 - Identificar e representar frações (menores e maiores que a unidade), associando-as ao resultado de uma divisão ou à ideia de parte de um todo, utilizando a reta numérica como recurso.
Objetivos específicos
Identificar frações menores e maiores que a unidade por meio da representação geométrica.
Conceito-chave
Frações maiores e menores que a unidade representadas em figuras geométricas.
Recursos necessários
- Caderno,
- atividade impressa,
- lápis de cor,
- lápis de escrever,
- régua,
- borracha.
Habilidades BNCC:
Objetivos de aprendizagem
Identificar frações maiores e menores que a unidade através da representação geométrica.
Resumo da aula
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar a proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: Apenas leia o objetivo para a turma, ressaltando a importância da colaboração dos alunos para atingir as metas estabelecidas para a aula.
Aquecimento
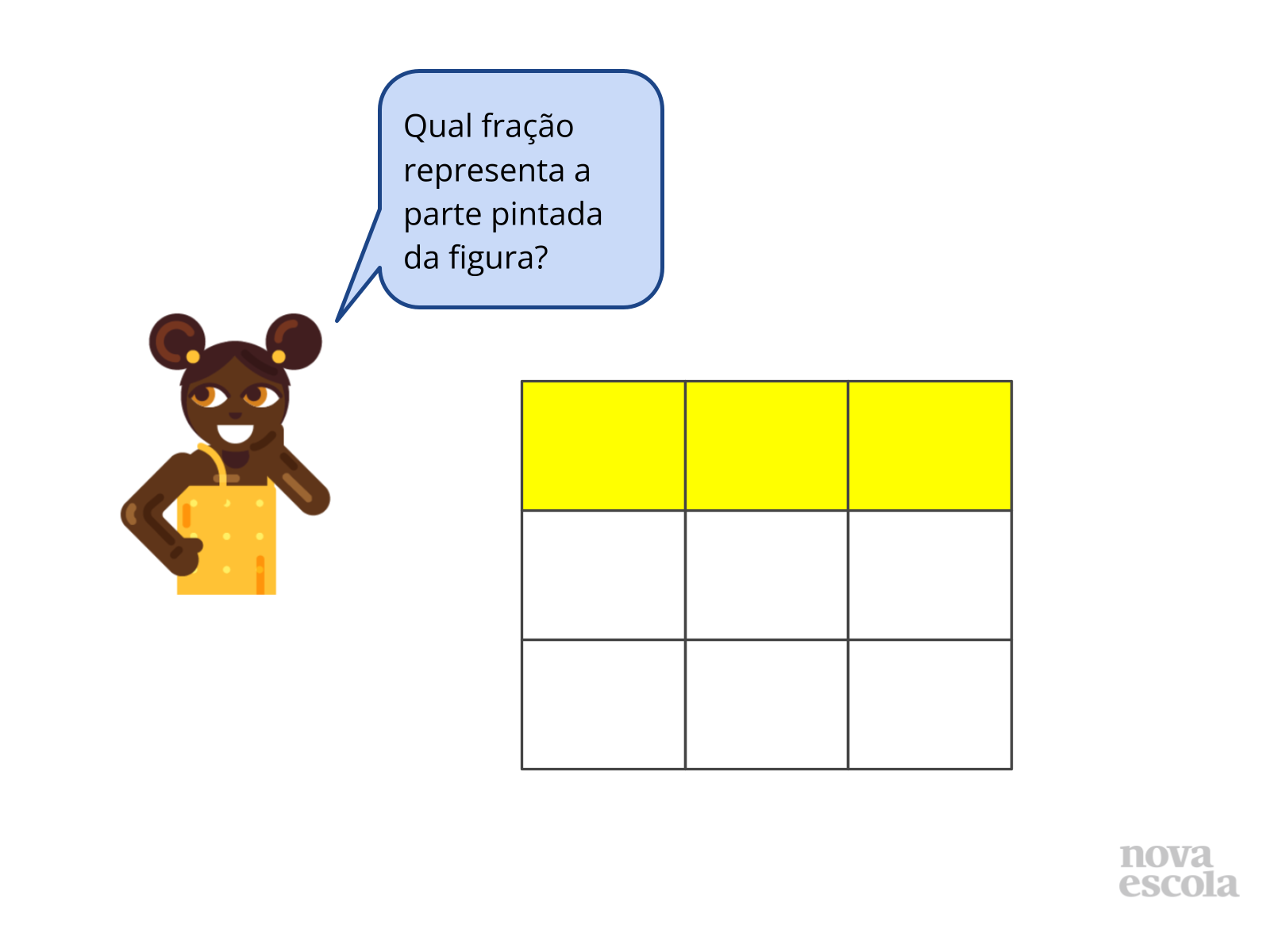
Tempo sugerido: 4 minutos.
Orientação: Antes de iniciar os questionamentos, é necessário lembrar aos alunos qual fração é a representação de uma ou mais partes de algo que foi dividido em partes iguais. Para tanto, é formada por um numerador e um denominador que variam de acordo com o que se representa.
Propósito: Retomar o conceito de representação fracionária por meio de figuras geométricas.
Discuta com a turma:
- Em quantas partes o retângulo foi dividido?
- Quantas partes estão pintadas?
- O que o denominador de uma fração representa? Em que parte da fração ele se localiza?
- O que o numerador de uma fração representa? Em que parte da fração ele se localiza?
- Qual o denominador correspondente à imagem apresentada? E qual o numerador?
- Como lemos a fração que representa esta figura?
- Se fossem coloridas cinco partes da figura, qual fração a representaria?
- E se fossem coloridas todas as partes da figura, qual fração a representaria?
- O que acontece com a fração quando pintamos todas as partes da figura?
- Que fração corresponde à parte que está sem pintar?
Atividade principal

Tempo sugerido: 15 minutos.
Orientação: Lembrar aos alunos que o total de partes que o chocolate possui irá compor o denominador da fração, pois ele representa o total de partes em que o inteiro foi dividido. O numerador será a quantidade de partes que cada uma receberá. A maneira como ele irá repartir o chocolate entre as meninas não influenciará na resposta. Desta forma, poderão surgir várias formas de representação fracionária para a quantidade que as meninas receberão, sendo todas elas frações menores que o inteiro.
Propósito: Identificar frações menores que a unidade por meio da representação geométrica
Discuta com a turma:
- Quantos pedaços tem a barra de chocolate? Qual deverá ser o denominador das frações? Por quê?
- Como você pode fazer para dividir a barra igualmente entre as três meninas?
- Quantos pedaços receberá cada menina?
Materiais complementares
Atividade principal

Tempo sugerido: 15 minutos.
Orientação: Relembrar aos alunos que o total de partes que o chocolate possui irá compor o denominador da fração. O numerador será a quantidade de partes que cada uma receberá. Assim, o que sofre mudanças é a representação do que foi distribuído, pois independentemente de quantas partes cada uma receba, o número de pedaços que cada chocolate possui não será alterado.
Propósito: Identificar frações maiores que a unidade por meio da representação geométrica.
Discuta com a turma:
- Quantos pedaços tem cada chocolate?
- O que uma fração representa?
- Qual deverá ser o denominador das frações? Por quê?
- Como você pode fazer para dividir as barras igualmente entre as três meninas?
- Cada uma das meninas receberá, mais ou menos que uma barra?
Discussão da solução
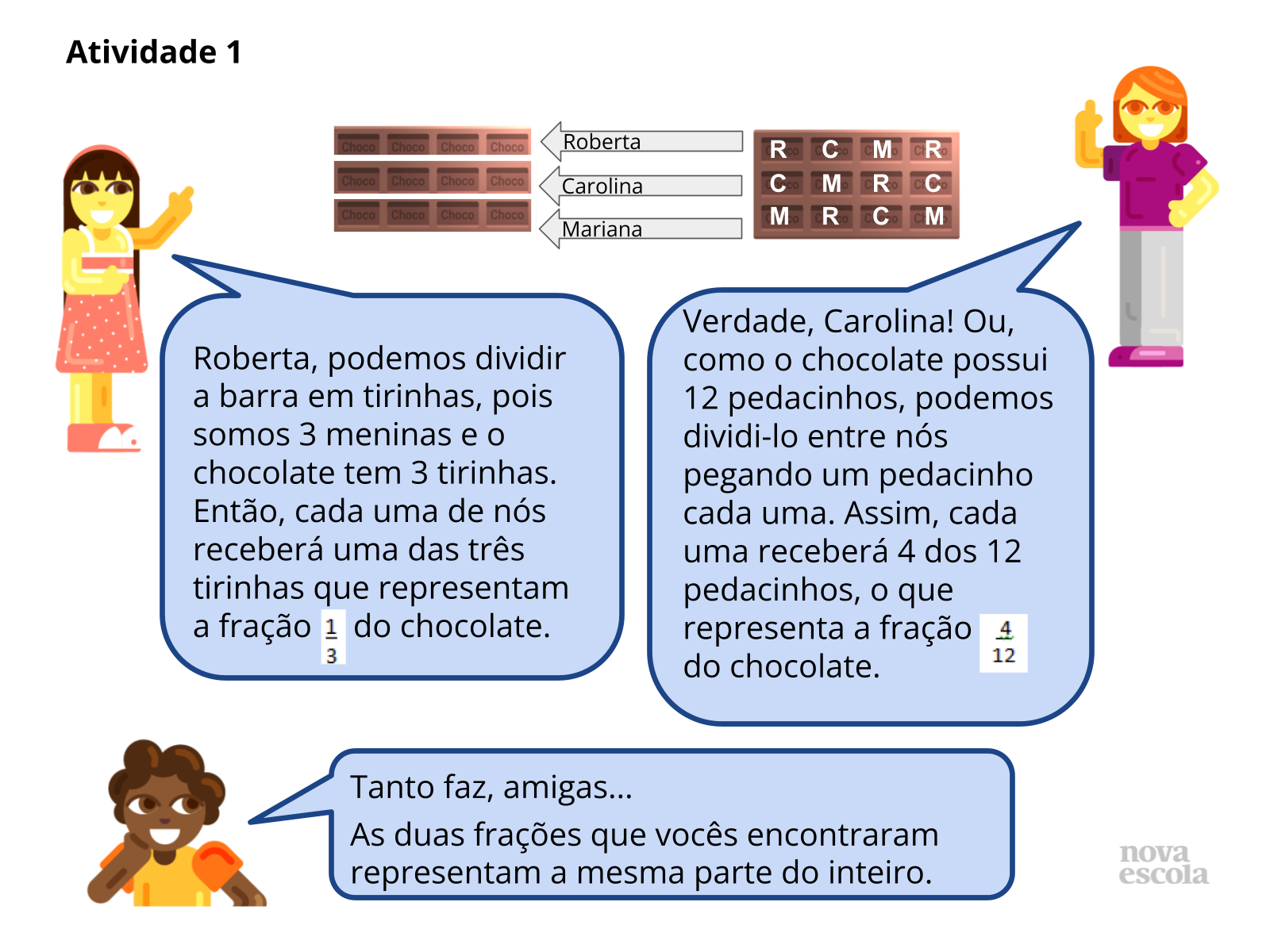
Tempo sugerido: 10 minutos.
Orientação: Deixar os alunos à vontade para realizar a divisão da maneira que acharem melhor. Pode ser dividindo pedacinho por pedacinho, pode ser dividindo o total de partes pela quantidade de meninas ou de outras formas que encontrarem. Apenas lembre aos alunos que devem formar uma fração com a quantidade de pedaços ou partes que cada menina irá receber em relação ao total de pedaços ou partes da barrinha de chocolate. Assim, podem aparecer frações equivalentes, como 4/12 e ?.
Propósito: Identificar frações menores que a unidade, a partir de divisões com representação geométrica de um inteiro.
Discuta com a turma:
- Quantos pedaços tem cada chocolate?
- Como você descobriu quantos pedaços cada menina recebeu?
- Que fração representa a quantidade de pedaços que cada menina recebeu?
- Quantas partes tem a barra de chocolate?
- Quantas partes cada menina receberá?
- Que fração corresponde à quantidade de partes que cada menina receberá?
- Alguma menina recebeu pedaços a mais?
- A fração encontrada é maior ou menor que o inteiro? Por quê?
Discussão da solução
Tempo sugerido: 10 minutos.
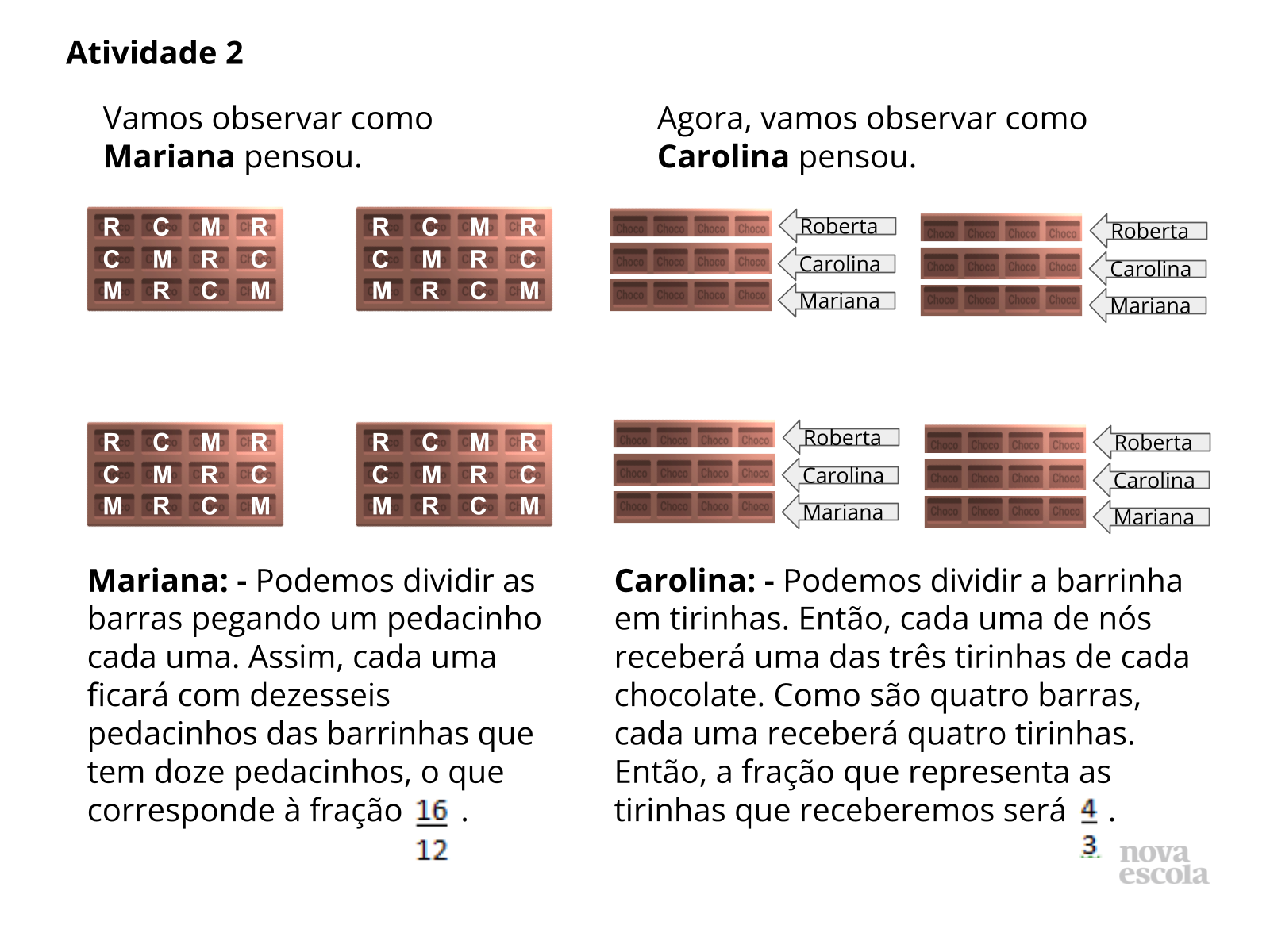
Orientação: Deixe os alunos à vontade para escolherem a melhor forma de repartir os chocolates. Caso seja necessário, pode-se imprimir barrinhas de chocolate iguais às da questão para que os alunos dividam pela quantidade de meninas. Como existem diferentes formas de se resolver a questão, deixe que os alunos apresentem-nas. Podem aparecer frações mistas, pois como são frações maiores que o inteiro, as crianças podem associar a uma barrinha e alguns pedacinhos.
Propósito: Identificar frações maiores que a unidade, a partir de divisões com representação geométrica de um inteiro.
Discuta com a turma:
- Quantos pedaços tem cada chocolate?
- Como você fez para descobrir com quantos pedaços de chocolate cada menina ficou?
- Esta quantidade é maior ou menor que a quantidade de pedaços que contém cada barra?
- Qual fração corresponde à quantidade de pedaços de chocolate que cada menina recebeu?
- Existe outra fração que representa a quantidade de pedacinhos que cada menina recebeu?
- Esta fração é maior ou menor que o inteiro? Por quê?
Discussão da solução

Tempo sugerido: 10 minutos.
Orientação: Instigue os alunos a perceberem que, se cada uma das meninas receber mais de uma barra inteira, pode-se repartir as barras, inicialmente, dando uma barra inteira para cada uma. É importante também mostrar aos alunos que o inteiro seriam as três tirinhas de uma das barras (a barra inteira), mais uma tirinha da outra barrinha. E esta quantidade, como representa mais de um inteiro, pode ser representado na forma fracionária e mista. Interessante, até abordar a representação da forma mista, mostrando associadas aos desenhos.
Propósito: Identificar frações maiores que a unidade, a partir de divisões com representação geométrica de um inteiro, representando tanto na forma mista como na fracionária.
Discuta com a turma:
- Nas soluções apresentadas anteriormente, cada menina ficou com mais ou com menos de uma barra de chocolate?
- Em quantos pedaços cada barra foi dividida?
- Quantas barras e quantas tirinhas cada menina receberá?
- De que outra maneira poderíamos iniciar essa divisão?
- Qual a diferença entre as frações apresentadas?
Sistematização do conceito
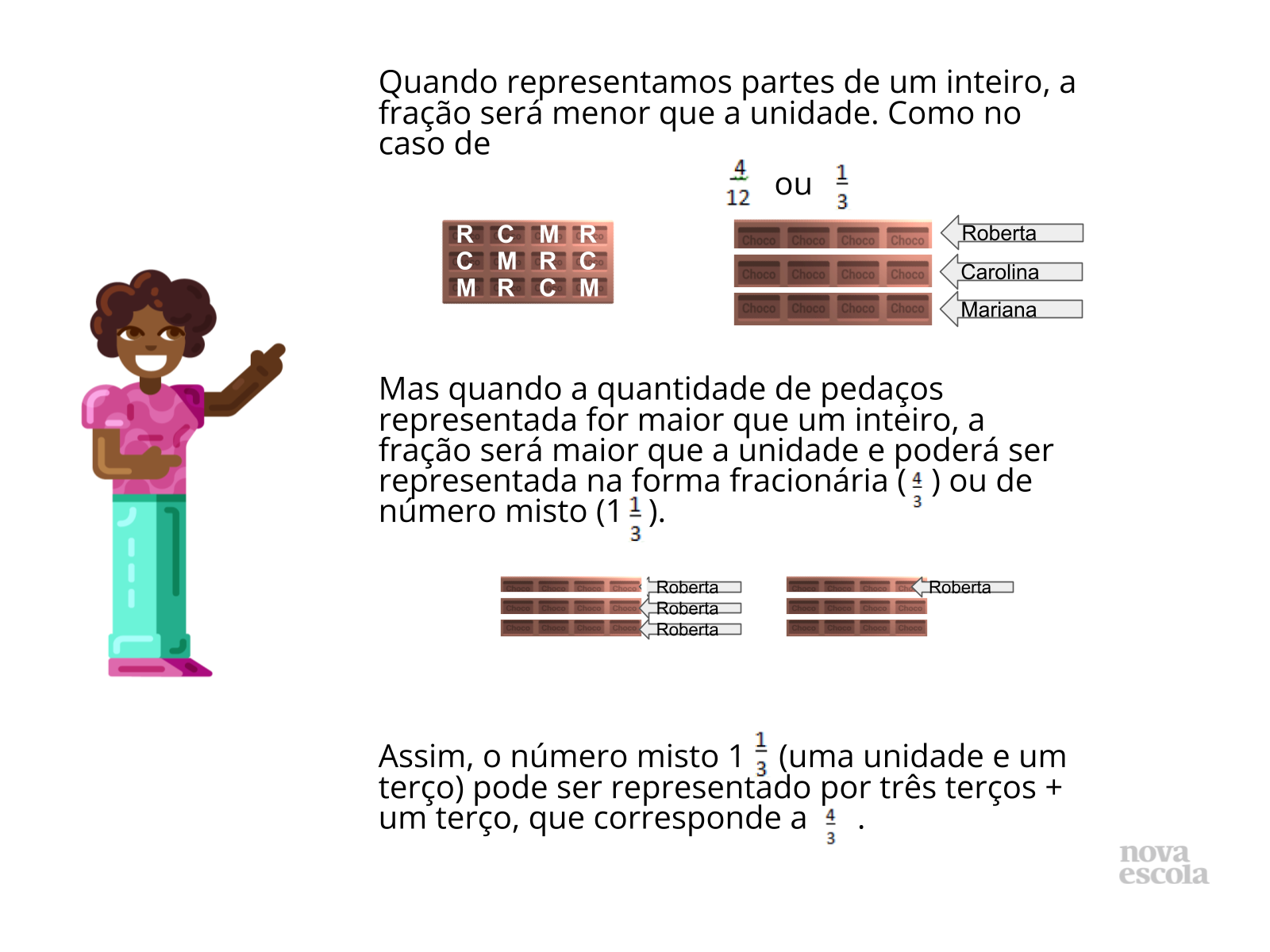
Tempo sugerido: 5 minutos.
Orientação: Para esta etapa, é necessário relembrar com os alunos como procederam para identificar frações maiores e menores que o inteiro, como também que as maiores podem ser representadas na forma mista e fracionária.
Propósito: Sintetizar as maneiras de se identificar frações maiores e menores que a unidade por meio de figuras geométricas.
Discuta com a turma:
- O que são frações maiores que a unidade? E menores?
- Como identificamos as frações maiores e menores que a unidade na atividade realizada?
Encerramento

Tempo sugerido: 4 minutos.
Orientação: Peça aos alunos que resumam, em uma frase, o que aprenderam durante a aula. Enfatize a representação geométrica das frações que foram apresentadas durante a aula. Anote os termos ou as palavras-chave no quadro e forme uma frase que resuma toda a aula.
Propósito: Resumir o que foi trabalhado durante a aula.
Discuta com a turma:
- A fração 4/12 precisou de quantas figuras para representá-la? E a fração 16/12?
- Qual a diferença entre frações maiores e menores que o inteiro?
Raio-X

Tempo sugerido: 10 minutos.
Orientações: Para facilitar a realização da atividade, a sala de aula deve estar organizada em semicírculo. Em seguida, peça que, individualmente, os alunos leiam a atividade e a realizem, analisando atentamente as imagens. Se necessário, deixe que redesenhem a figura para montar a fração. Em seguida, peça aos alunos que compartilhem com o colega ao lado as soluções e modos de representar a atividade. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
Propósito: Verificar se os alunos compreenderam como se identificar frações maiores e menores que a unidade por meio da representação geométrica.
Discuta com a turma:
- Como você começou a fazer a atividade?
- Como você comparou as duas imagens apresentadas na questão?
- De que forma você descobriu quem representou a fração maior e menor que a unidade?
- Como você montou a fração representada por cada criança?
- O que você percebeu ao comparar sua resposta com seu colega?
Materiais complementares
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano MAT5_05NUM04
Recursos
- Necessários: -
- Opcionais: -
Para este plano, foque na etapa Aquecimento, Atividade principal, Discussão das soluções e Encerramento
Aquecimento
Professor(a), você pode realizar o Aquecimento deste plano com seus alunos seja em uma aula síncrona ou assíncrona. Compartilhe com a turma o slide presente nesta atividade e solicite que tentem resolver o problema. Caso a aula esteja ocorrendo de forma síncrona permita que os alunos exponham suas resoluções e conversem entre si, mas caso esteja ocorrendo de forma assíncrona os estudantes podem enviar suas considerações/reflexões em formato de texto ou áudio. Compartilhe, em formato de texto, os questionamentos presentes no “Discuta com a turma” e solicite respostas em formato de texto ou áudio.
Atividade principal
Professor(a), compartilhe com a turma os problemas presentes nesta atividade e solicite que tentem resolvê-los. Você pode enviar as imagens dos slides ou enviar o documento com as atividades, você o encontra aqui: https://nova-escola-producao.s3.amazonaws.com/REAkpZE2UURs5EPy9y5UJxJADmwUACvk7cTetetXrd23TjwJAtGBap78THRP/ativaula-mat5-05num04.pdf. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas resoluções e, caso esteja ocorrendo de forma assíncrona, os estudantes podem enviar suas considerações/reflexões em formato de texto ou áudio.
Discussão das soluções
Professor(a), compartilhe com a turma a resolução da atividade e utilize os questionamentos presentes no “Discuta com a turma” para fomentar a reflexão dos problemas. Deixar para os alunos a leitura e interpretação dos slides dessa etapa da aula pode confundi-los. Então, caso a aula esteja ocorrendo de forma síncrona, sugerimos que você verbalize cada etapa da resolução mostrando um slide por vez. Caso a aula esteja ocorrendo de forma assíncrona, você pode gravar um vídeo mostrando os slides e refletindo as soluções propostas. Para tornar a resolução um pouco mais real você pode de fato filmar a divisão de barras de chocolate.
Encerramento
Professor(a), solicite que os estudantes escrevam, com suas palavras, o que compreenderam sobre a representação de frações maiores que a unidade. Compartilhe com os alunos o slide presente nesta etapa do plano de aula e peça que eles ilustrem um exemplo.
Raio X
O problema proposto no Raio X pode ser enviado em formato de imagem para os alunos e solicitado como uma “tarefa” a ser entregue em momento a ser combinado com a turma. Solicite que os alunos reproduzam o quadro de ordem em seus cadernos e então indiquem nele a altura mencionada.
Convite às famílias
Professor(a), sugira que os alunos joguem “Bolha Matemática” com seus familiares, o jogo pode ser acessado em https://www.digipuzzle.net/minigames/bubble/bubble_fractions.htm?language=portuguese&linkback=../../pt/jogoseducativos/matematica-fracoes/index.htm. Eles podem realizar uma competição para ver quem consegue atingir a maior quantidade de pontos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Cátia do Vale dos Santos Mendes
Mentor: Sônia Maria dos Santos Campos Neves
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF05MA03 - Identificar e representar frações (menores e maiores que a unidade), associando-as ao resultado de uma divisão ou à ideia de parte de um todo, utilizando a reta numérica como recurso.
Objetivos específicos
Identificar frações menores e maiores que a unidade por meio da representação geométrica.
Conceito-chave
Frações maiores e menores que a unidade representadas em figuras geométricas.
Recursos necessários
- Caderno,
- atividade impressa,
- lápis de cor,
- lápis de escrever,
- régua,
- borracha.