Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “
Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
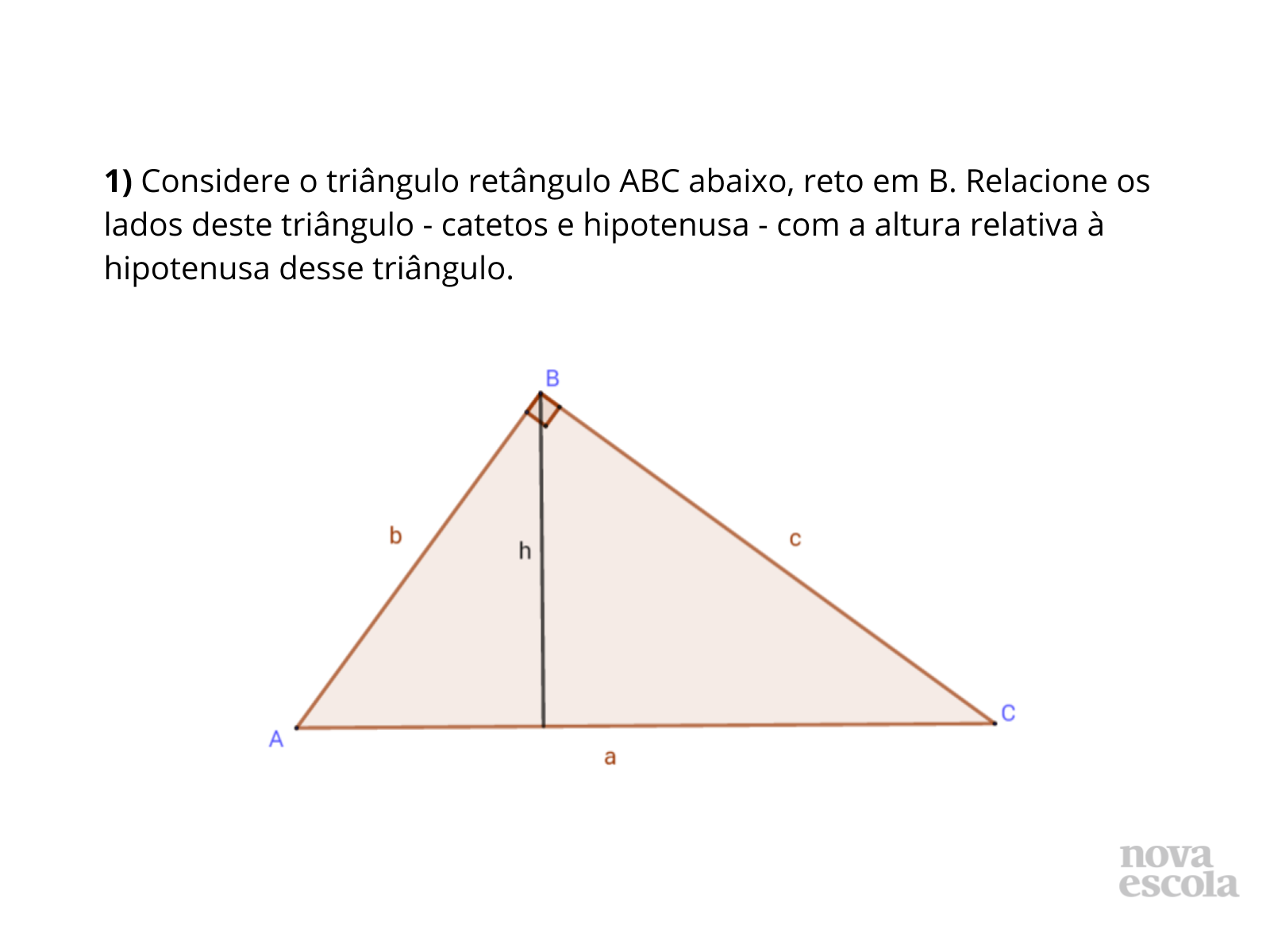
Objetivo
Tempo sugerido: 2 minutos.
Orientações: Levante com a classe hipóteses sobre a relação entre essas quatro medidas.
Obs.: o professor pode utilizar recortes e dobraduras, construções com régua e esquadro ou recursos computacionais como o GeoGebra. Neste plano específico, utilizaremos recursos computacionais, mas se a escola não dispor de computadores para os alunos, você pode realizar essa construção com régua e compasso, por exemplo. Uma outra opção é acessar outros Planos de Aula do Time de Autores NOVA ESCOLA, que contêm as relações anteriores.
Para acessar as outras metodologias, veja:
Com recortes
Com construções geométricas
Propósito: Despertar a curiosidade sobre a nova relação proposta e o interesse do uso de recursos tecnológicos.
Discuta com a turma:
- Há relação entre essas medidas?
- Como podemos verificar essa relação?
Aquecimento
Tempo sugerido: 10 minutos (slides 3 e 4) .
Orientações: Os alunos deverão estar na sala de informática. É bem possível que não tenha um computador por aluno mas o trabalho em duplas ou trios é muito importante, portanto seria interessante os alunos agrupados para realizar as atividades, já que o próprio programa é de fácil navegação e quase auto explicativo. Explorar os recursos disponíveis no programa desperta a curiosidade dos alunos para descobrir os comandos possíveis. Se for possível, os alunos podem levar notebooks para a escola e, se o professor só dispõe de um computador, faça as atividades todos juntos.
Propósito: Conhecer os recursos do Geogebra.
Discuta com a turma:
- Vocês conhecem outros programas computacionais de geometria dinâmica?
- Já utilizaram o Geogebra em outras situações?
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Aquecimento
Tempo sugerido: 10 minutos (slides 3 e 4) .
Orientações: Será proposta uma série de atividades para que os alunos aprendam a utilizar os principais recursos do GeoGebra, que será utilizado depois em sala de aula. Os alunos deverão realizar as construções com a orientação do professor.
Propósito: Familiarizar os alunos com os recursos disponíveis no software GeoGebra.
Discuta com a turma:
- Como posso realizar cada construção pedida?
- Quais ferramentas são necessárias para esta construção?
- Há mais de uma maneira de realizar a mesma orientação?
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Atividade Principal
Tempo sugerido: 20 minutos (slides 5 e 6).
Orientações: Os alunos irão construir o triângulo proposto conforme orientações para que depois façam as comparações das medidas e tentem encontrar alguma relação entre os lados.
Propósito: Construir triângulos no GeoGebra para perceber a relação entre os catetos, a hipotenusa e a altura de um triângulo retângulo.
Discuta com a turma:
- Como podemos realizar as construções pedidas?
- Há mais de uma maneira de realizá-las?
- Ao realizar as construções e medições, questione os alunos: O que é o lado AB? E o lado BC? E como é chamado o lado AC?
- No item 3 e 4, o aluno pode optar pela construção de um triângulo ABC no lugar de traçar os dois segmentos. Deixe-o resolver pelo método que achar melhor.
- Ao chegar ao item 6, questione: por que preciso traçar a perpendicular? - Lembre-os do objetivo da aula, que é relacionar a medida dos catetos, da hipotenusa e da altura relativa à hipotenusa no triângulo retângulo.
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal
Tempo sugerido: 20 minutos (slides 5 e 6).
Orientações: Neste momento, os alunos deverão encontrar qual a relação entre as medidas. Para isso, construa os itens de a a e pois ajudará o aluno a tirar as conclusões por eles mesmos.
Propósito: Incentivar os alunos para perceber a relação entre as medidas pedidas.
Discuta com a turma:
- O que foi acontecendo com os produtos ao mover os vértices do triângulo?
- O novo triângulo modificou todas as medidas?
- A relação percebida no triângulo anterior se mantém?
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão da Solução
Tempo sugerido: 5 minutos.
Orientações: O professor deve ouvir cada grupo sobre as medidas encontradas.
Propósito: Discutir as soluções encontradas.
Discuta com a turma:
- Quais os valores encontrados pelo seu grupo?
- As medidas confirmam a relação encontrada?
- Há valores que foram aproximados? Por que isso ocorre?
- Como foram construídos os triângulos? Algum grupo realizou uma construção diferente?
Professor, como o GeoGebra não dispões da ferramenta “Construção de triângulo retângulo”, alguns alunos podem ter optado em construir apenas triângulos e medir o ângulo de 90º. Na primeira construção, isso não gera problemas, mas quando houver a movimentação do vértice B ou C, o triângulo pode deixar de ser retângulo, com isso as relações de igualdade deixam de ser verdadeiras. Verifique a construção realizada por cada grupo.
Se houver tempo e achar interessante, você pode propor aos alunos que realizem a construção de uma outra maneira.
Sistematização do Conceito
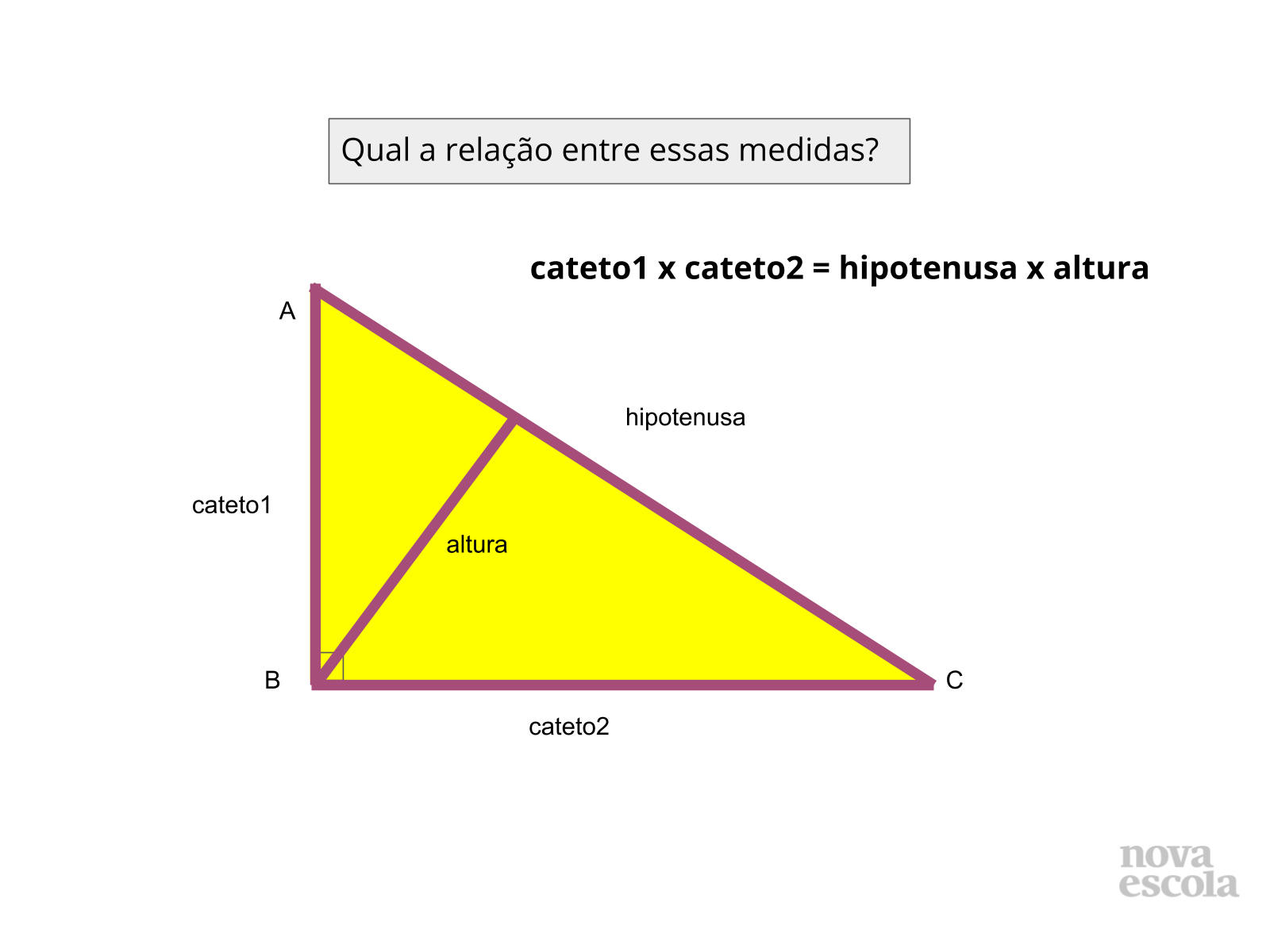
Tempo sugerido: 4 minutos (slides 8 e 9).
Orientações: Reafirmar a relação descoberta em aula. Retome todos os conceitos trabalhados em sala.
Propósito: Reforçar a relação descoberta em sala pelos alunos.
Discuta com a turma:
- 1º: Dado um triângulo retângulo ABC reto em B, como são chamados os lados? - chamamos os catetos de cateto1 e cateto2 para não gerar dúvida de que poderia ser cateto ao quadrado.
- 2º: Quantas alturas tem um triângulo?
- Qual a relação entre os catetos, a hipotenusa e a altura relativa a ela?
No próximo slide, há uma exemplo numérico onde o professor pode explorar a aplicação da nova relação.
Sistematização do Conceito
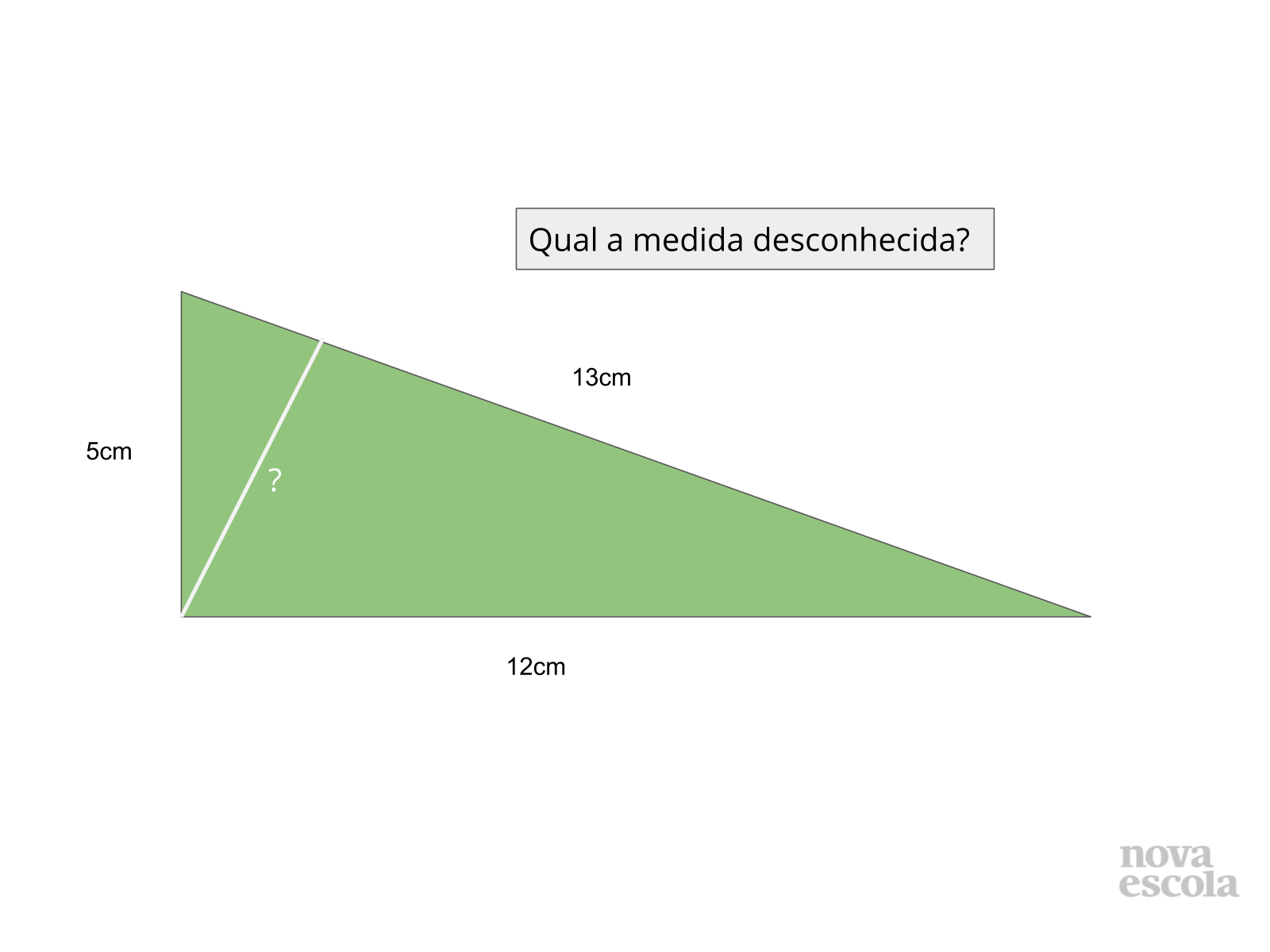
Tempo sugerido: 4 minutos (slides 8 e 9).
Orientações: Reafirmar a relação descoberta em aula.
Propósito: Reforçar a relação descoberta em sala pelos alunos.
Resolução:
Para descobrir o valor pedido, basta aplicar a relação:
5 . 12 = 13 . ?
60/13 = 4,6 aproximadamente.
Encerramento
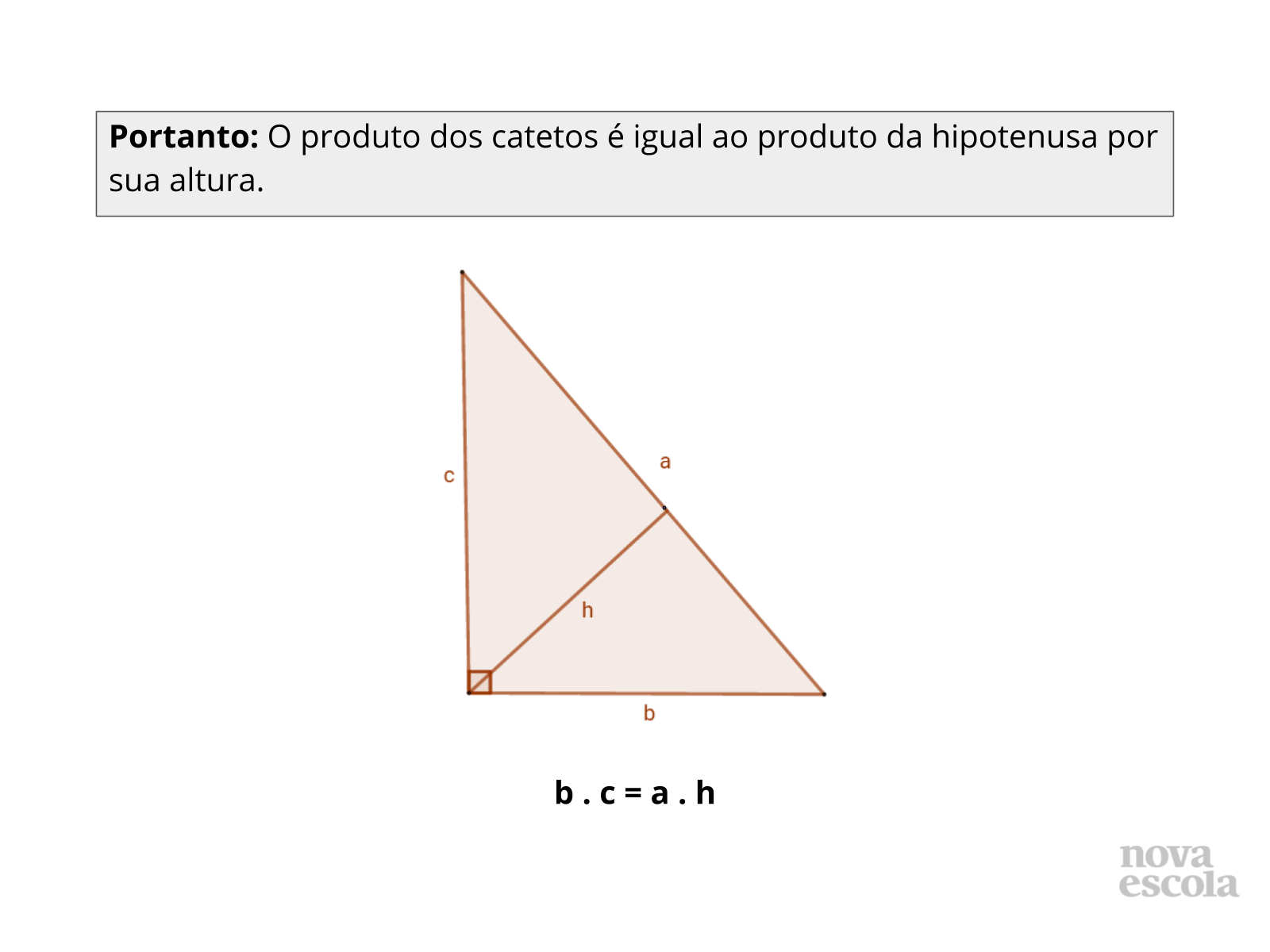
Tempo sugerido: 2 minutos.
Orientações: Esse slide vai reafirmar a nova relação entre as medidas do triângulo retângulo. É importante o professor ressaltar que essa relação não se mantém se o triângulo não for retângulo.
Propósito: Organizar os conhecimentos aprendidos.
Discuta com a turma:
- Preciso usar essas letras para representar a relação?
- Posso chamar os catetos de c? Ressalte que se utilizar a mesma letra deverá ter a mesma medida. Isso é possível, mas nem sempre é verdade. Apenas será válido se o triângulo for isósceles.
Raio X
Tempo sugerido: 7 minutos (slides 11 e 12).
Orientações: a aplicação deste exercício é simples e tem como objetivo verificar se os alunos se apropriaram da nova relação métrica.
Propósito: verificar a compreensão dos alunos.
Resolução:
10. a = 6 . 8
10 . a = 48
a = 48/10
a = 4,8
R: A altura relativa à hipotenusa mede 4,8 cm.
Discuta com a turma:
- Houve alguma dificuldade na resolução do exercício?
Materiais complementares:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar
