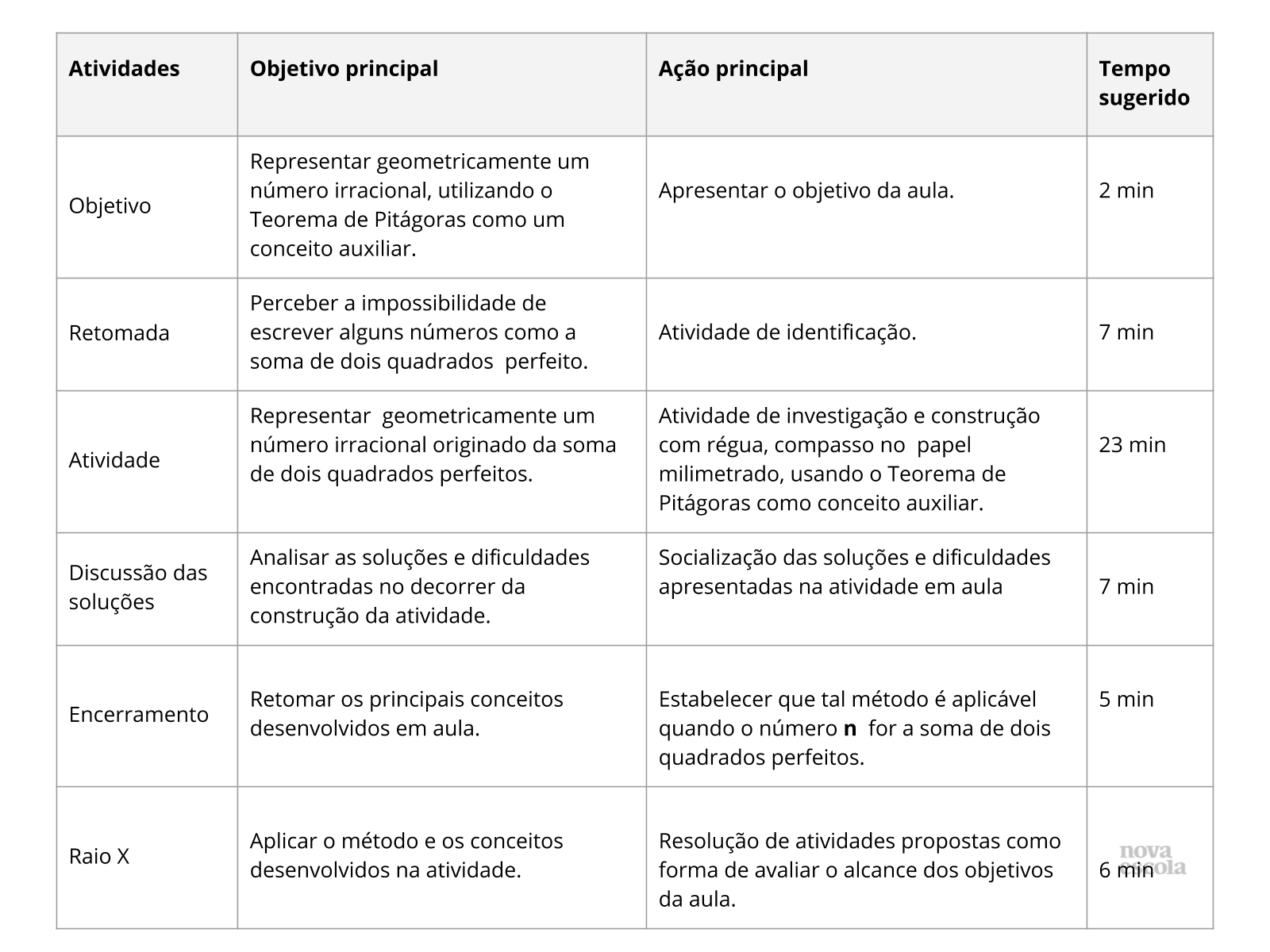
Resumo da aula
Título:
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Apresente o objetivo da aula de forma clara, de modo que os alunos percebam o que se deseja alcançar com as atividades a serem desenvolvidas na aula.
Propósito: Apresentar o objetivo da aula.
Discuta com a turma:
- Quando um número é dito irracional?
- O que significa “representar geometricamente um número”?
Retomada

Tempo sugerido: 7 minutos (slides 3 e 4) .
Orientações: Apresente para os alunos a pergunta.
Propósito: Rever conceitos relacionados a potenciação e escrita de um número como a soma de dois números naturais quadrados perfeitos
Discuta com a turma:
- Todo número pode ser escrito como a soma de dois números naturais quadrados perfeitos?
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Retomada

Tempo sugerido: 7 minutos (slides 3 e 4) .
Orientações: Proponha aos alunos que iniciem com a soma na qual a 1º parcela seja o número 1. Mostre que a propriedade comutativa, a + b = b + a, representa a mesma soma nos números naturais.
Propósito: Rever conceitos relacionados a potenciação e escrita de um número como a soma de dois números naturais quadrados perfeitos.
Discuta com a turma:
- Ao aumentarmos uma unidade na 1º parcela, o que deve ser feito na segunda parcela para que a soma permaneça 10?
- Todo número pode ser escrito como a soma de dois números naturais quadrados perfeitos?
Atividade Principal

Tempo sugerido: 23 minutos (slides 5, 6, 7, 8, 9, 10).
Orientações: Disponibilize papel milimetrado régua, lápis e compasso caso os alunos não possuam, garantindo a execução da atividade.
Propósito: Representar geometricamente um número irracional, utilizando o Teorema de Pitágoras como conceito auxiliar.
Discuta com a turma:
- Qual a diferença fundamental entre um número racional e um irracional?
- O que significa representar geometricamente um número?
Materiais Complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal

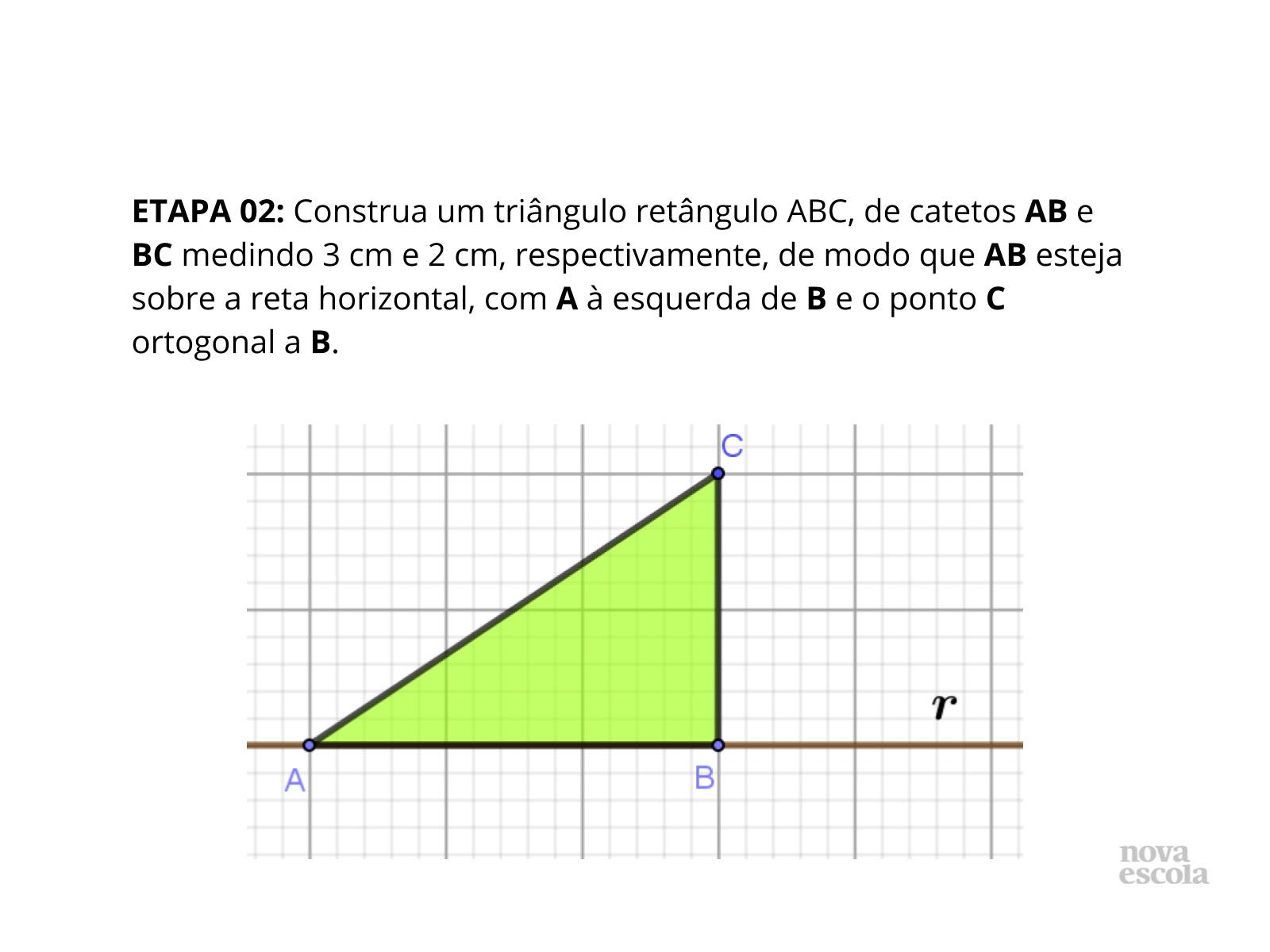
Tempo sugerido: 23 minutos (slides 6, 7, 8, 9, 10 e 11).
Orientações: Caso necessário, sugira que construa a reta suporte utilizando a linha horizontal, como forma de garantir a perpendicularidade quando for traçado os catetos do triângulo na etapa seguinte.
Propósito: Representar geometricamente um número irracional, utilizando o Teorema de Pitágoras como conceito auxiliar.
Discuta com a turma:
- O que é uma reta suporte?
Materiais Complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal
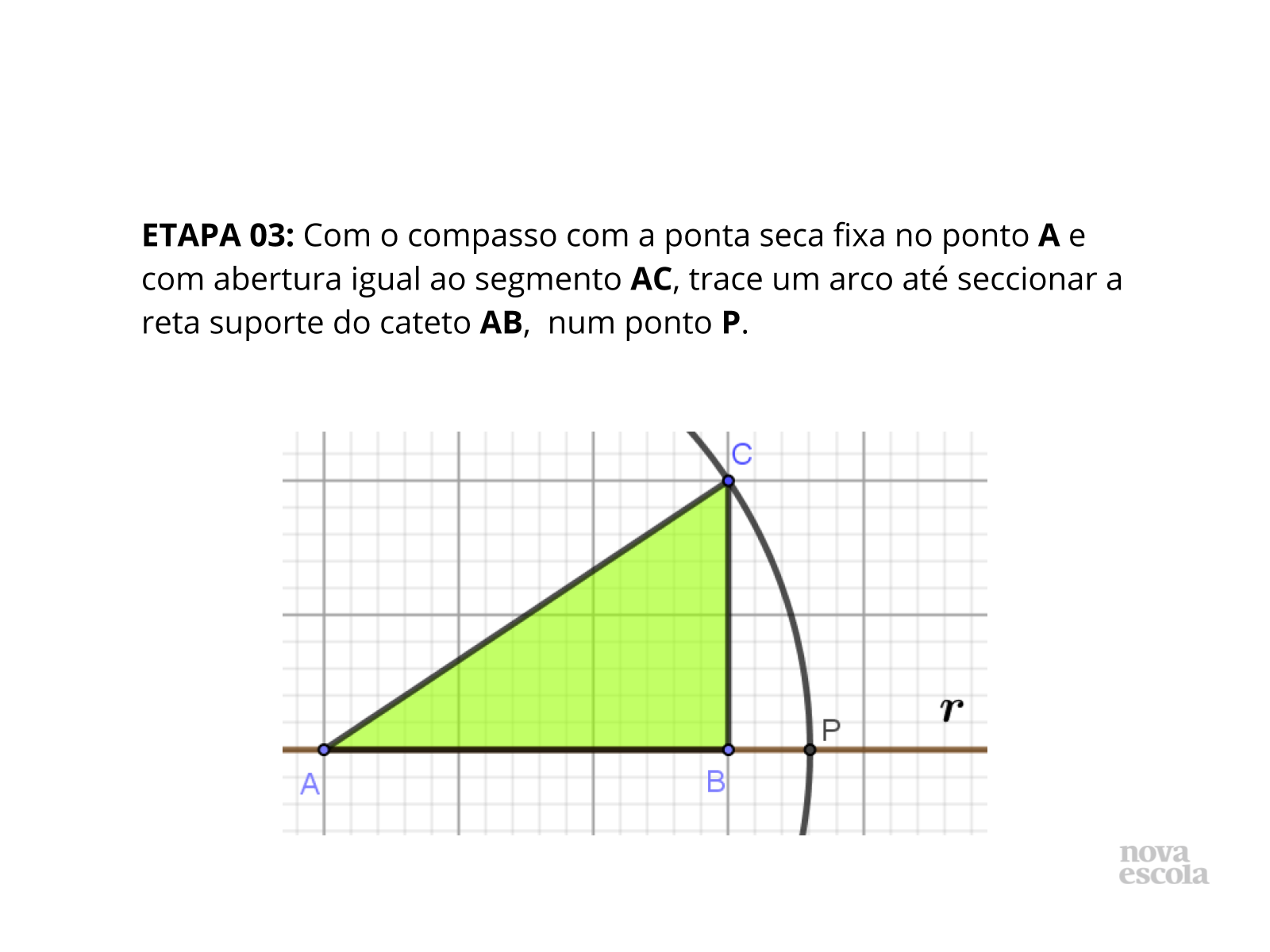
Tempo sugerido: 23 minutos (slides 6, 7, 8, 9, 10 e 11).
Orientações: Oriente os alunos a construírem o triângulo de modo que os catetos fiquem sobre as linhas da malha, garantindo, assim, a perpendicularidade entre os mesmos. É importante os alunos construírem o cateto maior (AB) na horizontal.
Propósito: Representar geometricamente um número irracional, utilizando o Teorema de Pitágoras como conceito auxiliar.
Discuta com a turma:
- O que garante a perpendicularidade dos catetos do triângulo construído?
Materiais Complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal
Tempo sugerido: 23 minutos (slides 6, 7, 8, 9, 10 e 11).
Orientações: Um ponto que merece atenção diz respeito ao manuseio correto do compasso, bem como do cuidado na tomada da abertura, de modo a assegurar uma boa aproximação para a representação na reta do número irracional em questão, assim como o domínio do sistema de numeração decimal, já que estaremos trabalhando com aproximações. Outro fator indispensável à consecução dos objetivos da atividade é o cuidado que o professor deverá ter com o tipo de papel milimetrado, que deve ser aquele com malhas de um centímetro com 5 subdivisões de 2 mm cada. O professor deverá disponibilizar tal papel para os alunos.
Propósito: Representar geometricamente um número irracional, utilizando o Teorema de Pitágoras como conceito auxiliar.
Discuta com a turma:
- A reta suporte representa qual conjunto numérico?
- Na reta numérica em questão, o ponto A representa qual número?
- Em quantas partes está dividida uma unidade no papel milimetrado?
- Qual a medida de cada parte em que está sub-dividida a unidade?
Materiais Complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal

Tempo sugerido: 23 minutos (slides 6, 7, 8, 9, 10 e 11).
Orientações: Oriente os alunos sobre o significado da divisão no papel milimetrado. Adotar uma aproximação de uma casa decimal.
Propósito: Representar geometricamente um número irracional utilizando o Teorema de Pitágoras como conceito auxiliar.
Discuta com a turma:
- Quanto mede cada um dos 5 segmentos que formam uma unidade no papel milimetrado?
- O número estimado na calculadora apresenta um período?
- O que isso significa?
Materiais Complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal

Tempo sugerido: 23 minutos (slides 6, 7, 8, 9, 10 e 11).
Orientações: Caso necessário, sugira os alunos a decompor os números em somas de dois números naturais. Baseados na decomposição anterior, os alunos deverão perceber que 5 = 1² + 2², e construir um triângulo retângulo de catetos medindo 1cm e 2cm respectivamente. No caso de raiz quadrada de 7, deverão concluir que 7 não pode ser escrito como a soma de dois quadrados perfeitos, o que torna inviável tal método para representar a raiz quadrada de 7.
Propósito: Representar geometricamente um número irracional utilizando o Teorema de Pitágoras como conceito auxiliar.
Discuta com a turma:
- De quantos modos é possível escrever 5 como a soma de dois números naturais?
- É possível escrever 5 como a soma de dois quadrados perfeitos?
- É possível escrever 7 como a soma de dois quadrados perfeitos?
Materiais Complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão das soluções

Tempo sugerido: 7 minutos.
Orientações: Estimule os alunos a socializarem suas hipóteses e dificuldades na representação geométrica da raiz quadrada de valor n, de modo a perceberem a limitação de tal método, ou seja, que somente poderá ser aplicado quando n for a soma de dois quadrados perfeitos, como no caso, 13 = 3² + 2². Já no caso do 7, tal método apresentará limitações, já que os quadrados perfeitos menores que 7 são 1 = 1², 4 = 2², e a soma desse par não representa 7. De modo análogo, não havendo possibilidade de estabelecer soma 15 com um par de quadrados perfeitos menores que 15 (1 = 1², 4 = 2², 9 = 3²).
Propósito: Discutir a solução e as dificuldades apresentadas no decorrer da atividade
Discuta com a turma:
- O método desenvolvido apresenta alguma limitação?
Encerramento

Tempo sugerido: 5 minutos.
Orientações: Encerre a aula resumindo com os alunos o conceito desenvolvido.
Propósito: Sintetizar o que foi desenvolvido na aula.
Discuta com a turma:
- Todo número irracional pode ser representado pelo método desenvolvido em aula?
Raio X

Tempo sugerido: 6 minutos.
Orientações: Conduza os alunos no sentido de que utilizem o Teorema de Pitágoras como um auxiliador na construção e representação de segmentos incomensuráveis, ou seja, represente geometricamente números irracionais. Para tanto, é necessário que os alunos saibam utilizar régua e compasso.
Propósito: Avaliar se os objetivos da aula foram alcançados.
Discussão com a turma:
- Com as medidas estabelecidas para os catetos, como obter a medida da hipotenusa?
- A medida da hipotenusa será representada por um número racional ou irracional?
Materiais Complementares:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar