Resumo da aula
Título:
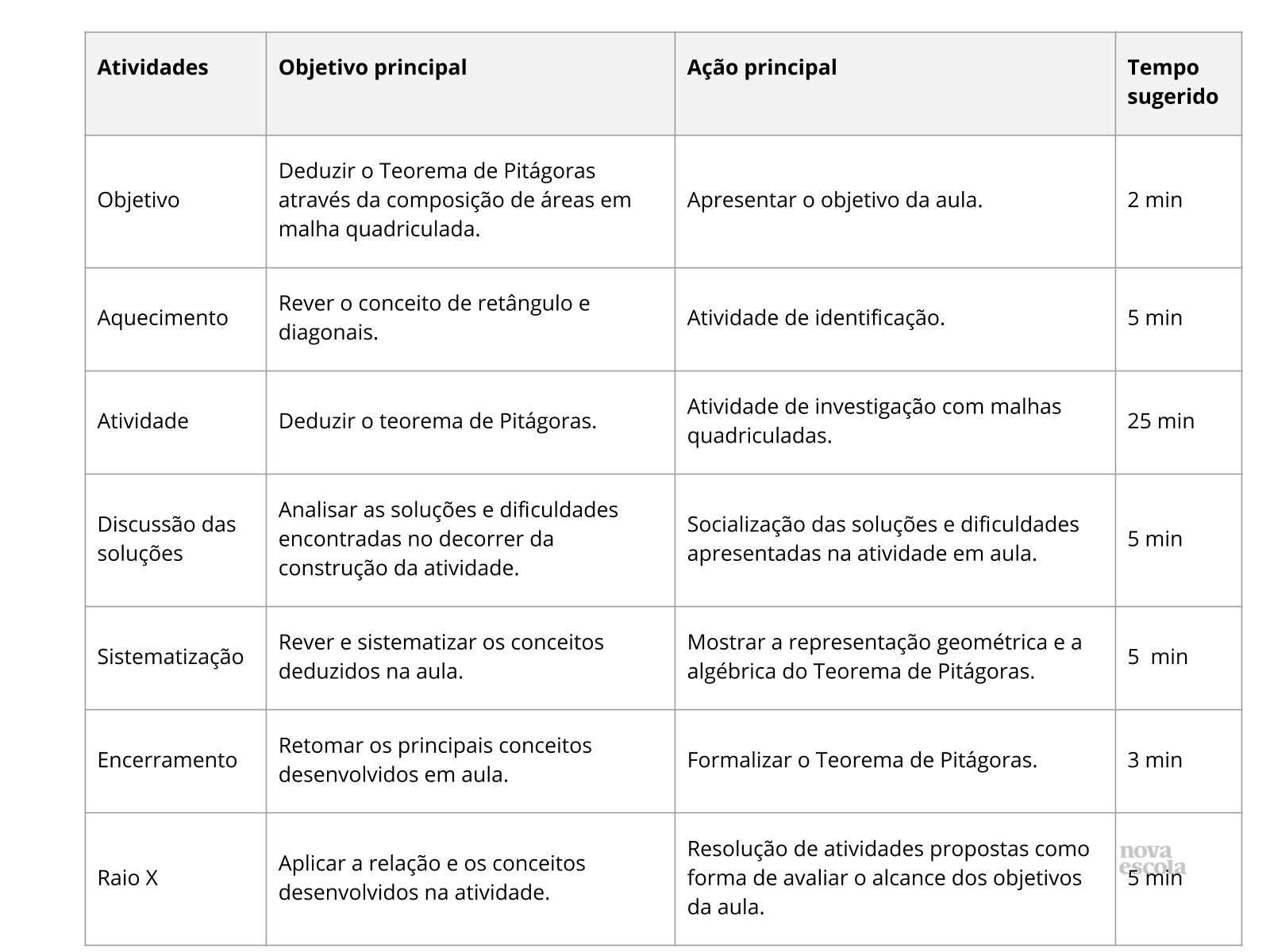
Objetivo

Título:
Tempo sugerido: 2 minutos.
Orientações: Apresente o objetivo da aula de forma clara, de modo que os alunos percebam o que se deseja alcançar com as atividades a serem desenvolvidas na aula.
Propósito: Apresentar o objetivo da aula.
Discuta com a turma:
Aquecimento
Título:
Tempo sugerido: 5 minutos (slides 3 e 4) .
Orientações: Solicite que os alunos realizem a atividade e circule pela sala verificando sua realização.
Propósito: Rever conceitos relacionados aos quadriláteros, em especial ao retângulo.
Discuta com a turma:
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Aquecimento
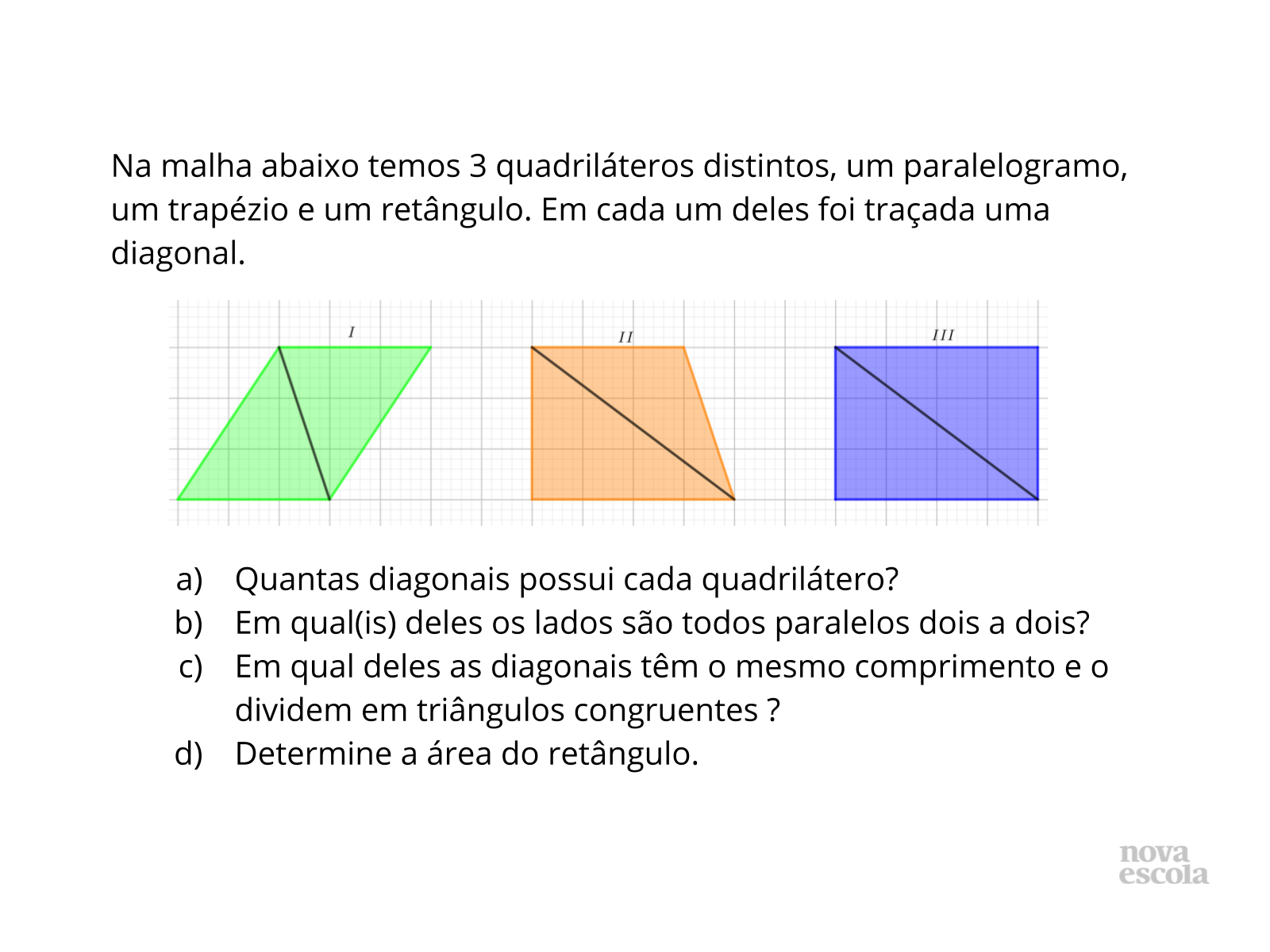
Título:
Tempo sugerido: 5 minutos (slides 3 e 4) .
Orientações: Solicite que os alunos realizem a atividade e circule pela sala verificando sua realização.
Propósito: Rever conceitos relacionados aos quadriláteros, em especial ao retângulo.
Discuta com a turma:
- Quando um quadrilátero é retângulo?
- O que é uma diagonal?
- Como se calcular a área um retângulo sem a contagem na malha quadriculada?
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Atividade Principal

Título:
Tempo sugerido: 25 minutos (slides 5, 6, 7 e 8).
Orientações: Introduza a aula revendo alguns conceitos básicos essenciais ao desempenho das atividades.
Propósito: Deduzir o Teorema de Pitágoras com uso de malhas quadriculadas e composição de áreas.
Discuta com a turma:
- Como se chamam os segmentos que representam as medidas dos lados de um triângulo retângulo?
- Quando dois triângulos são congruentes ?
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Atividade Principal

Título:
Tempo sugerido: 25 minutos (slides 5, 6, 7 e 8).
Orientações: Oriente os alunos a construírem o triângulo de modo que os catetos fiquem sobre as linhas da malha, garantindo assim a perpendicularidade entre os mesmos. Oriente os alunos a construírem o cateto maior (AB) na horizontal. Caso façam diferente, porém, não irá alterar a resolução.
Propósito: Construir um quadrado sobre a hipotenusa com triângulos congruentes como suporte para a dedução do Teorema de Pitágoras.
Discuta com a turma:
- Quantos triângulos diferentes podem ser construídos com as dimensões dadas a partir de um ponto fixo sobre a malha e com os catetos sobre as linhas da malhas ?
- O que é a diagonal de um retângulo?
- Quantas diagonais há em um retângulo?
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Atividade Principal
Título:
Tempo sugerido: 25 minutos (slides 5, 6, 7 e 8).
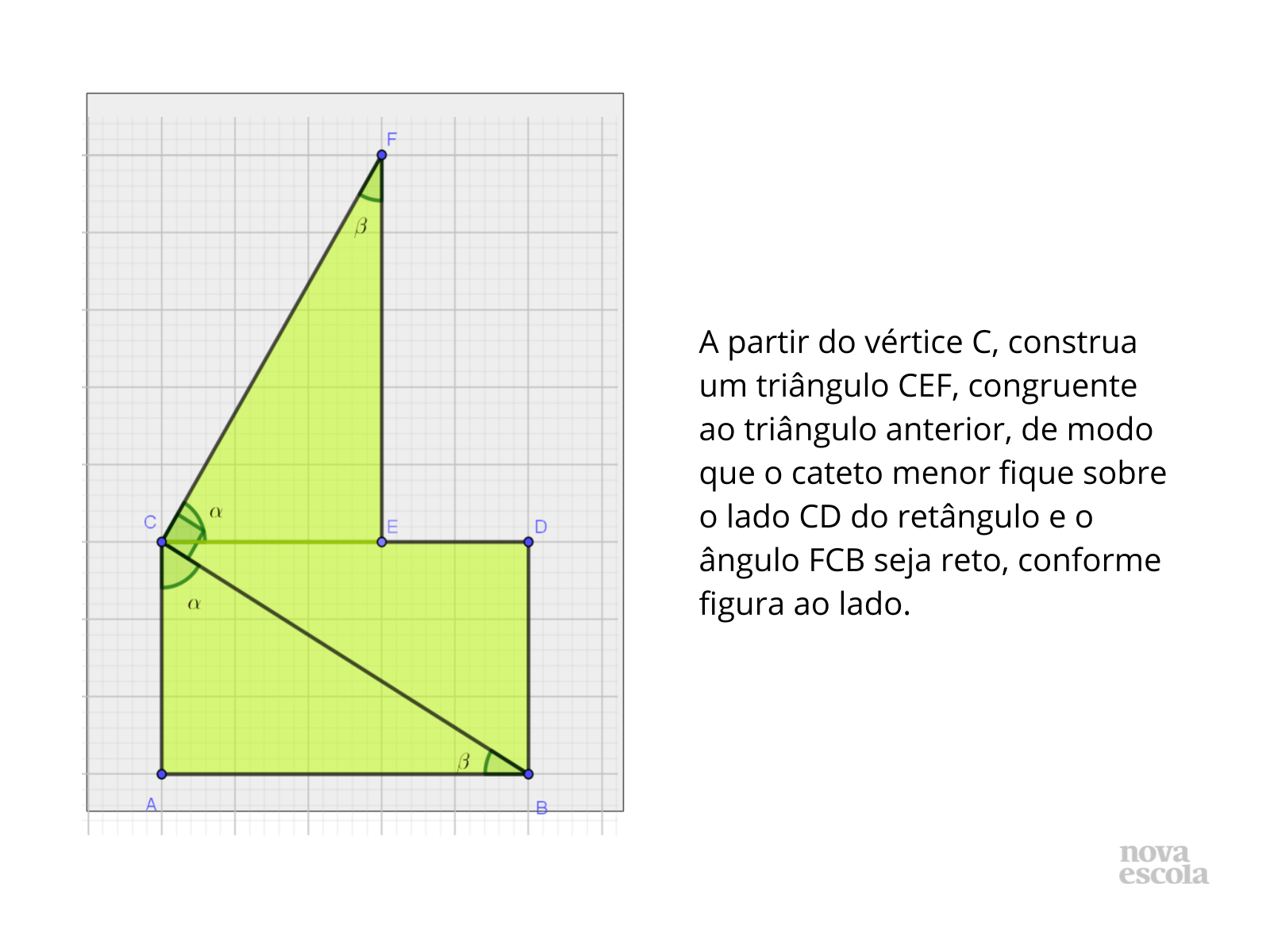
Orientações: O fato de garantir que o vértice E fique alinhado com o lado CD não assegura que o aluno irá construir o triângulo congruente que interessa a resolução, por isso a necessidade de mostrar essa etapa inicial. No entanto, poderíamos deixar em aberto a construção, mas, certamente, isso tomaria bem mais tempo até os alunos perceberem e identificarem o caminho a ser seguido. Lembramos que a aula é de 50 minutos e a atividade principal tem um tempo máximo de 25 minutos para execução pelos alunos.
Propósito: Construir um quadrado sobre a hipotenusa, como suporte para a dedução do Teorema de Pitágoras
Discuta com a turma:
- Quanto vale a soma dos ângulos interno de um triângulo?
- Quando dois ângulos são complementares?
- Quanto mede cada ângulo interno do quadrado?
- Quanto vale a soma dos ângulos agudos de cada triângulo retângulo?
- O que garante a congruência dos triângulos construídos?
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Atividade Principal

Título:
Tempo sugerido: 25 minutos (slides 5, 6, 7 e 8).
Orientações: Esta é a etapa em que os grupos irão concluir a construção e, através da atividade, propor alguma hipótese. É essencial que os alunos construam a hipótese de que a área sobre a hipotenusa é igual a soma das áreas sobre cada cateto.
Propósito: Deduzir e generalizar o Teorema de Pitágoras.
Discuta com a turma:
- Há alguma relação entre as áreas dos três quadrados?
- Será que este fato é verdadeiro para todo triângulo retângulo?
- Supondo verdadeira a hipótese construída, como se representa matematicamente, de modo geral?
Materiais complementares:
Aquecimento
Resolução do Aquecimento
Discussão das soluções

Título:
Tempo sugerido: 5 minutos.
Orientações: Estimule os alunos a socializarem suas hipóteses e dificuldades.
Propósito: Discutir a solução e as dificuldades apresentadas no decorrer da atividade.
Discuta com a turma:
- A relação deduzida é válida para outros triângulos?
Sistematização
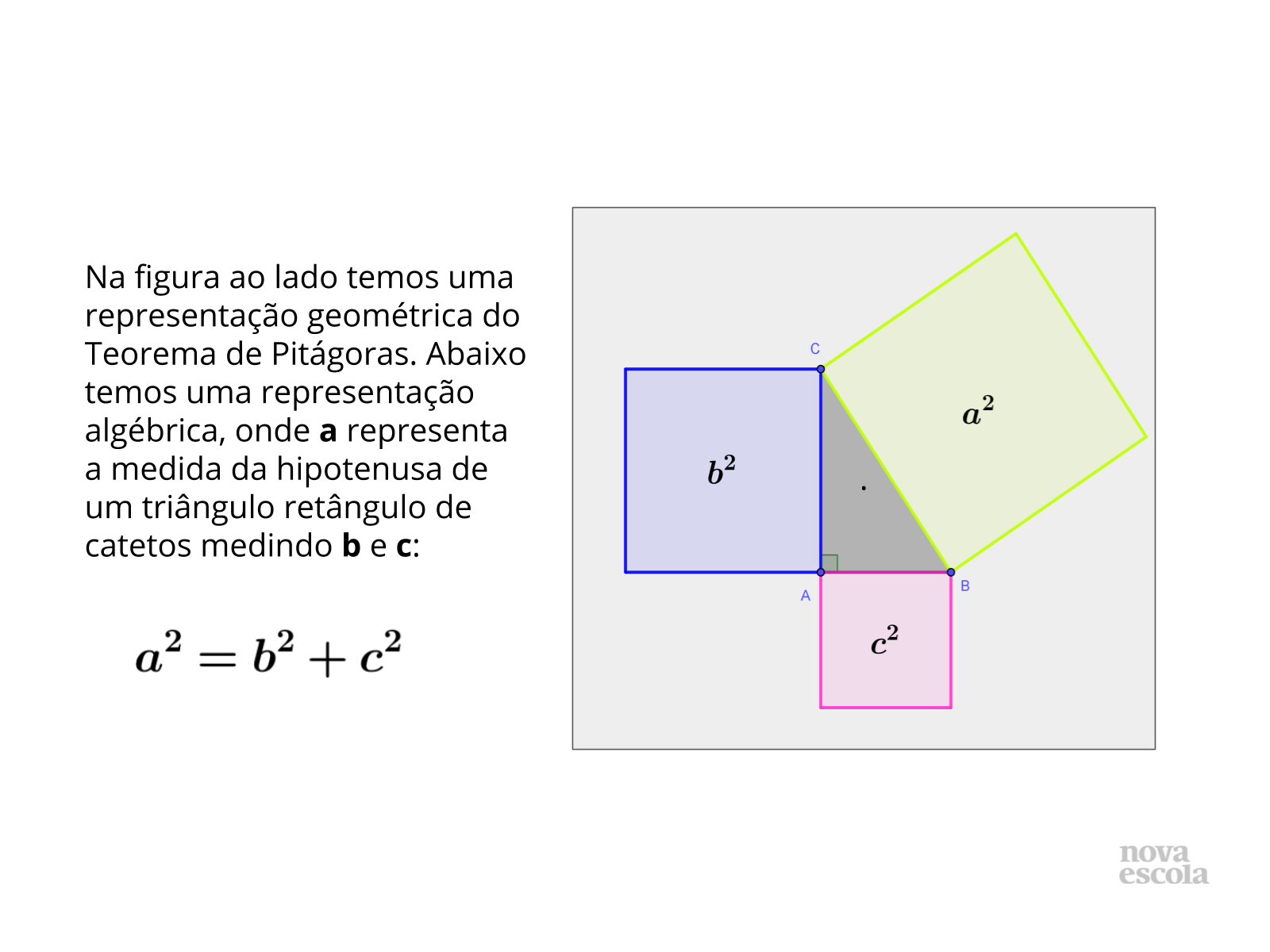
Título:
Tempo sugerido: 4 minutos.
Orientações: Leia o slide com os alunos e sistematize o que foi estudado durante a atividade.
Propósito: Sintetizar o conceito desenvolvido na aula.
Discuta com a turma:
- Por que essa relação é denominada de Teorema de Pitágoras ?
Encerramento

Título:
Tempo sugerido: 4 minutos.
Orientações: Leia o encerramento com os alunos e solicite que registrem no caderno.
Propósito: Formalizar o que foi desenvolvido na aula.
Discuta com a turma:
- Como representar genericamente tal resultado?
Raio X
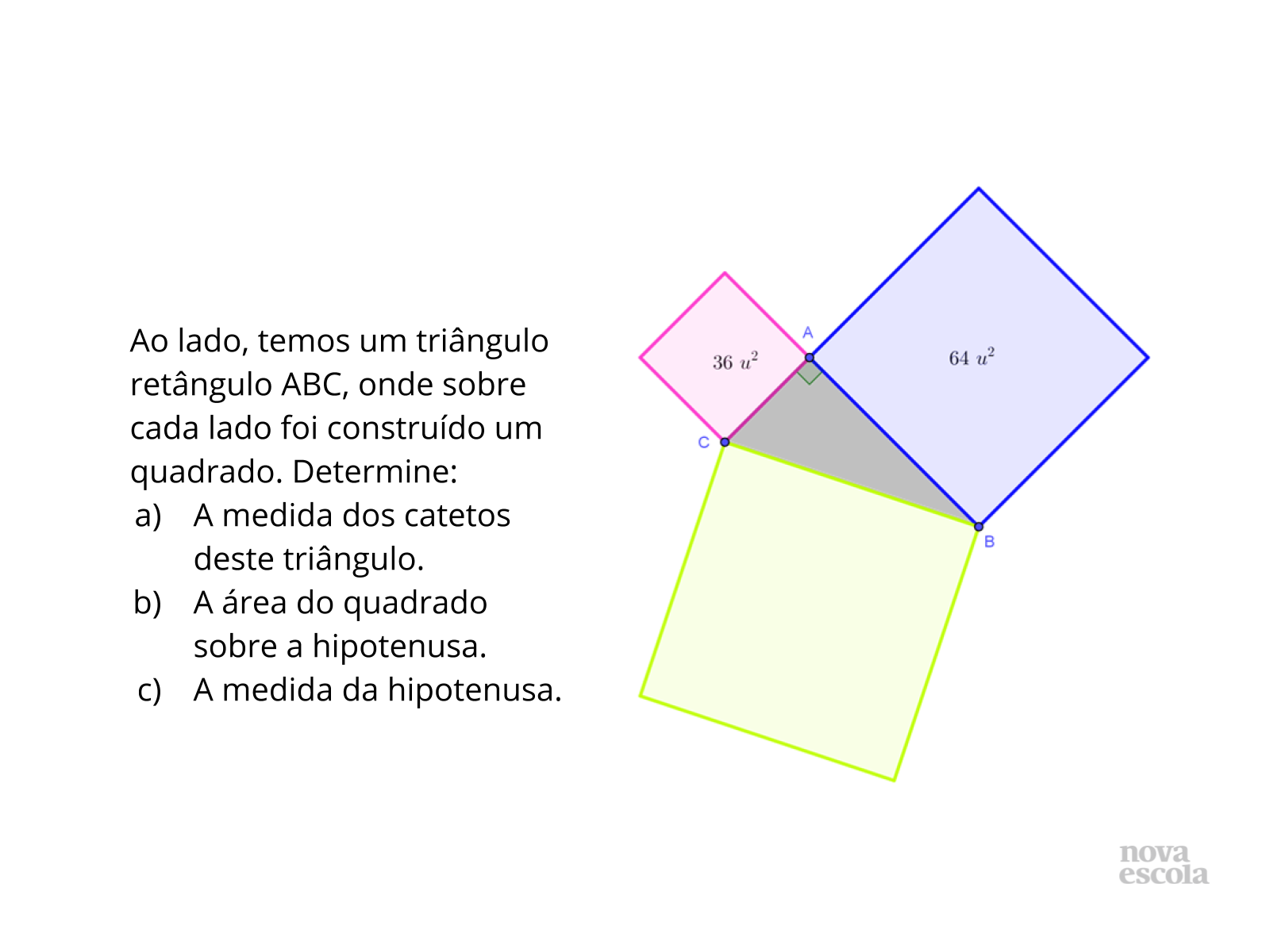
Título:
Tempo sugerido: 5 minutos.
Orientações: O raio X deve ser resolvido individualmente, como forma do professor avaliar o alcance dos objetivos na turma como um todo.
Propósito: Verificar a aprendizagem dos conceitos desenvolvidos em sala de aula.
Discuta com a turma:
- Qual a área de um quadrado de lado l?
- Como calcular a medida do lado de um quadrado a partir da área do mesmo?
Materiais Complementares
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar