Aquecimento
Plano de Aula
Plano de aula: Investigando áreas e ângulos em triângulos
Plano 1 de uma sequência de 11 planos. Veja todos os planos sobre Teorema de Pitágoras e suas aplicações
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Sebastiao Rodrigues da Silva
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
(EF09MA14) Resolver e elaborar problemas de aplicação do Teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
Objetivos específicos
Identificar o triângulo retângulo como o caso em que ocorre a igualdade da soma das áreas menores com a área sobre o lado maior (Hipotenusa)
Conceito-chave
Exploração intuitiva do Teorema de Pitágoras.
Recursos necessários
- Computador
- Software GeoGebra
- Projetor
- Lápis, régua e compasso
- Malha quadriculada
- Atividades impressas
Habilidades BNCC:
Objetivos de aprendizagem
Identificar o triângulo retângulo como o caso em que ocorre a igualdade da soma das áreas menores com a área sobre o lado maior (Hipotenusa)
Resumo da aula
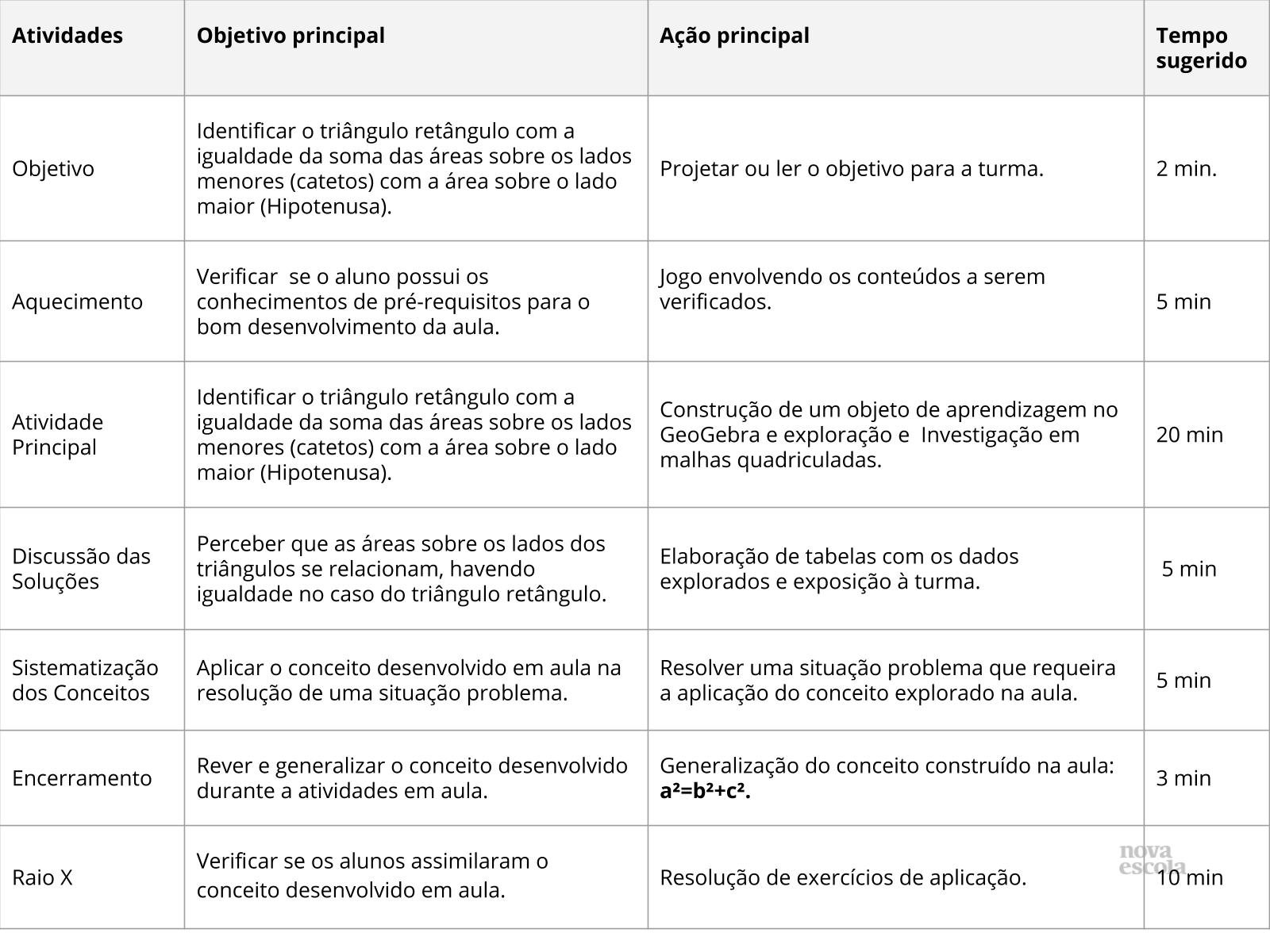
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Título:
Tempo Sugerido: 2 minutos.
Orientações:
Projete ou leia o objetivo para a turma. É importante que fique claro o que se pretende alcançar com as atividades da aula.
Propósito: Compartilhar com a turma o objetivo da aula.
Discussão com a turma: Verifique se a turma domina os conceitos de ângulos, triângulos e área:
- O que é ângulo?
- Qual a característica fundamental de um triângulo retângulo?
- O que é área? Como se calcula a área de um quadrado?
Aquecimento

Tempo sugerido: 5 minutos. (slides 3 e 4).
Orientações:
Observe o desempenho dos alunos na resolução da atividade de aquecimento e proponha caminhos, caso necessário, para que eles alcancem o conhecimento necessário, além de discutir com a turma as soluções apresentadas. Leia com os alunos e explique as regras do jogo.
Propósito: Verificar se o aluno possui os conhecimentos tidos como pré-requisitos para o bom desenvolvimento da aula.
Discuta com a turma:
- É possível determinar a medida do ângulo destacado sem o uso do transferidor?
- Quando um ângulo é obtuso? Quando um triângulo é isósceles?
Aquecimento

Tempo sugerido: 5 minutos. (slides 3 e 4).
Orientações:
Observe se o aluno domina a classificação de triângulos quanto a medida dos lados e dos ângulos, bem como a determinação de ângulos entre segmentos sem o uso do transferidor.
Propósito: Verificar se o aluno possui os conhecimentos tidos como pré-requisitos para o bom desenvolvimento da aula.
Discuta com a turma:
- É possível determinar a medida do ângulo destacado sem o uso do transferidor?
- Quando um ângulo é agudo? Quando um triângulo é retângulo?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 5, 6, 7 e 8).
Orientações:
Oriente os alunos em cada passo de construção do objeto no GeoGebra. Caso não tenha acesso ao recurso tecnológico, o professor poderá propor a construção, em grupos, em malha quadriculada, de diferentes triângulos com os respectivos quadrados sobre os lados e sugerir que os alunos investiguem as relações entre as áreas do quadrado maior com a soma das outras duas áreas menores, pedindo para que cada grupo relate suas hipóteses. (Proposta alternativa desenvolvida nos slides 9, 10 e 11).
Propósito: Identificar o triângulo retângulo como o caso em que ocorre a igualdade da soma das áreas menores com a área sobre o lado maior (hipotenusa).
Discuta com a turma: Aproveite oportunidade da construção com Geogebra para explorar alguns conceitos matemáticos.
- O que é segmento?
- Quando duas retas são paralelas?
- O que é um polígono regular?
- Como se calcula a área de um quadrado?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 5, 6, 7 e 8) .
Orientações:
Oriente os alunos em cada passo de construção do objeto no GeoGebra. Caso não tenha acesso ao recurso tecnológico, o professor poderá propor a construção, em grupos, em malha quadriculada, de diferentes triângulos com os respectivos quadrados sobre os lados e sugerir que os alunos investiguem as relações entre as áreas do quadrado maior com a soma das outras duas áreas menores, pedindo para que cada grupo relate suas hipóteses. (Proposta alternativa desenvolvida nos slides 9, 10 e 11).
Propósito: Identificar o triângulo retângulo como o caso em que ocorre a igualdade da soma das áreas menores com a área sobre o lado maior (hipotenusa).
Discuta com a turma: Aproveite oportunidade da construção com Geogebra para explorar alguns conceitos matemáticos.
- O que é segmento?
- Quando duas retas são paralelas?
- O que é um polígono regular?
- Como se calcula a área de um quadrado?
Atividade Principal
Tempo sugerido: 20 minutos. (slides 5, 6, 7 e 8) .
Orientações:
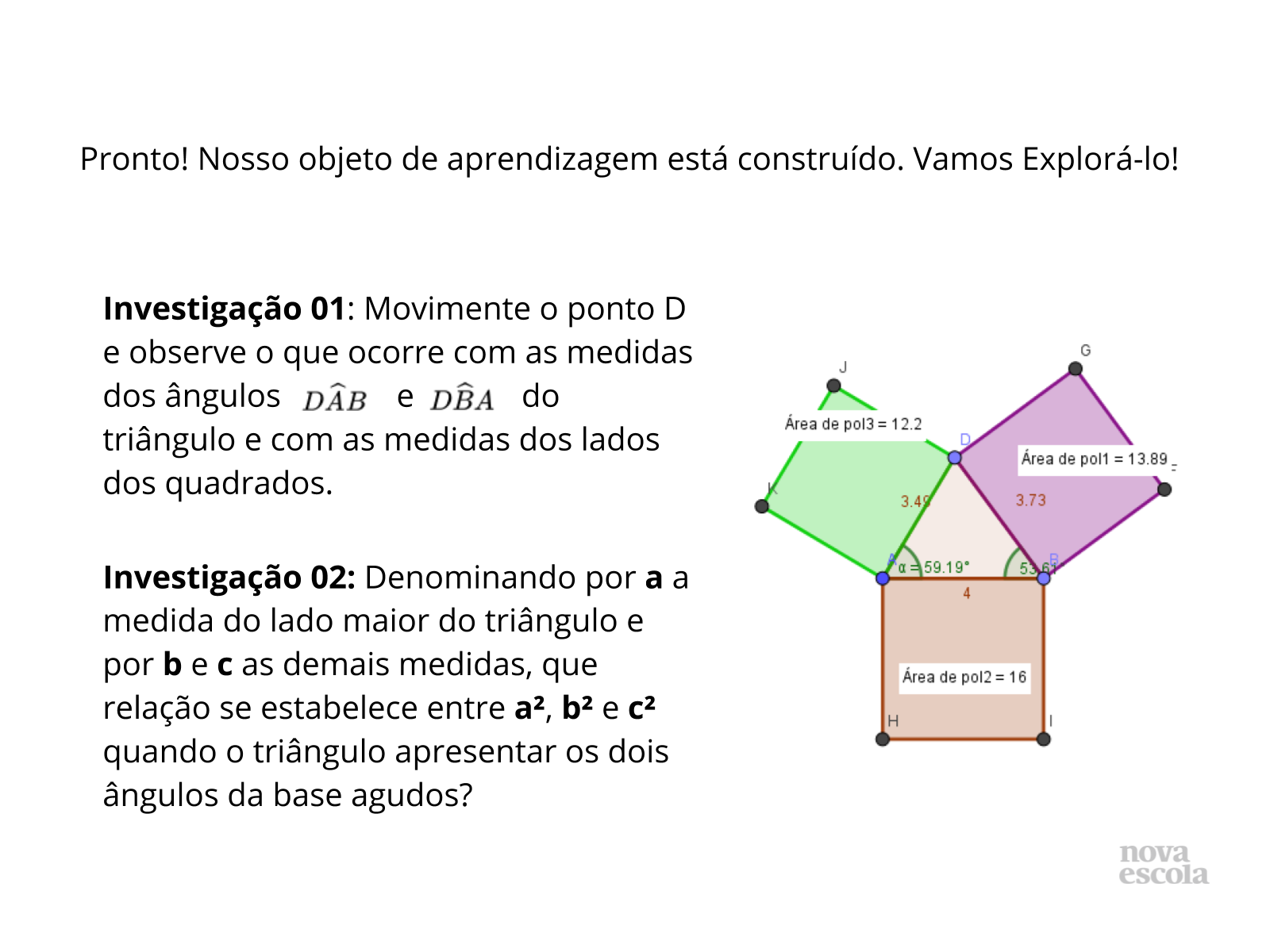
Proponha que as investigações sejam realizadas em grupos de no máximo 3 alunos para que haja uma troca de ideias melhor da equipe. Oriente os alunos ao movimentarem o ponto D a observarem o que ocorre com a figura e tomarem anotações de suas conjecturas. Como mencionado anteriormente, tal atividade poderá ser adaptada para malhas quadriculadas (slides 9, 10 e 11).
Propósito: Explorar o objeto de aprendizagem construído no GeoGebra.
Discuta com a turma:
- O que ocorre com os ângulos quando variamos a posição do ponto D?
- O que ocorre com as áreas dos quadrados quando variamos a posição do ponto D?
- Fixando um ângulo da base, podemos afirmar que a área do quadrado sobre o lado oposto ao ângulo depende da medida do ângulo?
- O que acontece quando os ângulos da base são iguais?
Atividade Principal
Tempo sugerido: 20 minutos. (slides 5, 6, 7 e 8) .
Orientações:
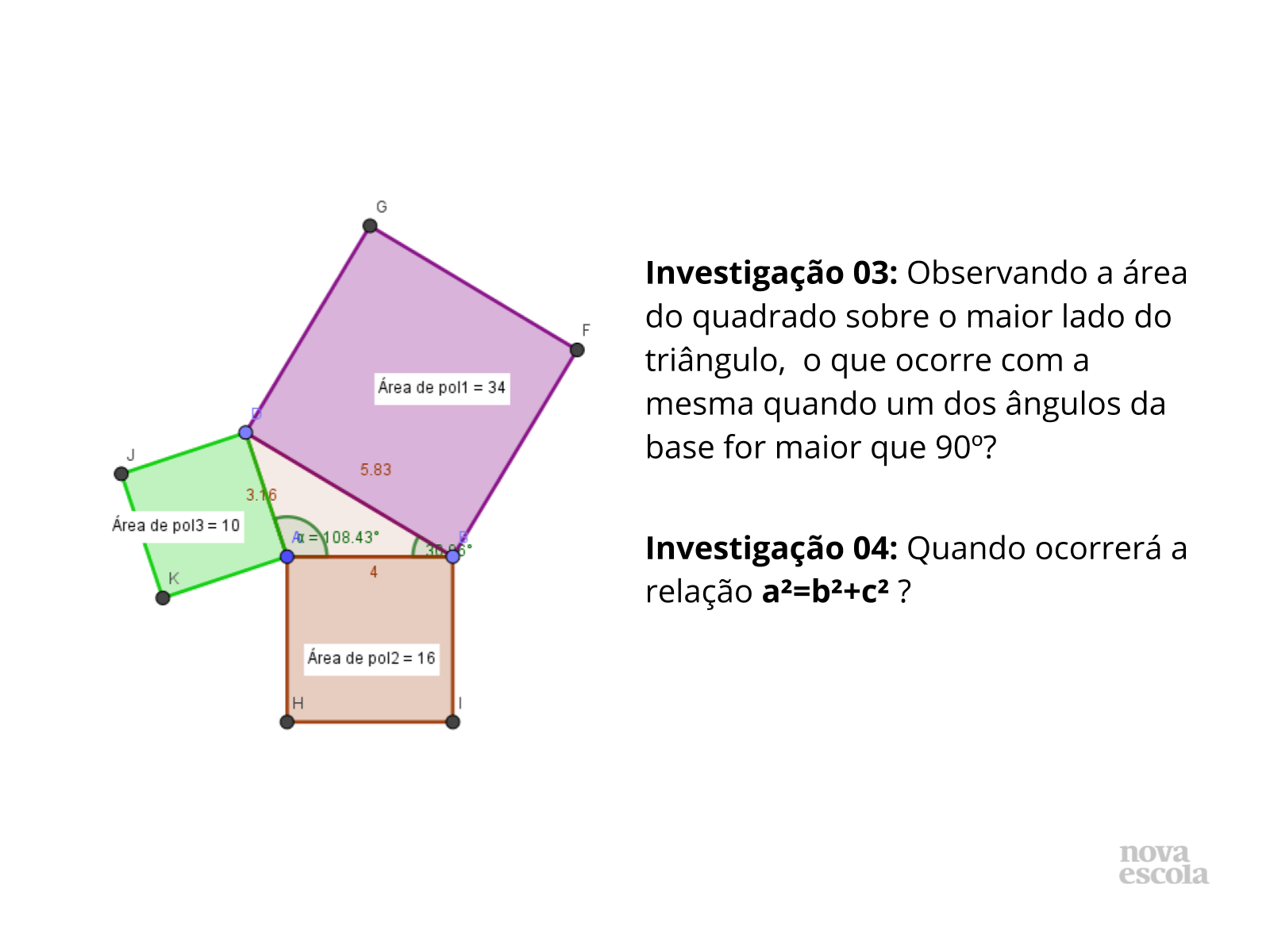
Proponha que as investigações sejam realizadas em grupos de no máximo 3 alunos para que haja uma troca de ideias melhor da equipe. Oriente os alunos, ao movimentarem o ponto D, a observarem o que ocorre com a figura quando o ângulo DBA for maior que 90º, testando sua hipótese para diversos valores deste ângulo, tomando anotações de suas conjecturas.
Propósito: Identificar o triângulo retângulo como o caso em que ocorre a igualdade da soma das áreas menores com a área sobre o lado maior (Hipotenusa).
Discuta com a turma:
- O que ocorre com os ângulos quando variamos a posição do ponto D?
- O que ocorre com as áreas dos quadrados quando variamos a posição do ponto D?
- Fixando um ângulo da base, podemos afirmar que a área do quadrado sobre o lado oposto é tanto maior quanto maior for ângulo?
Atividade Principal
Tempo sugerido: 20 minutos. (slides 9, 10 e 11).
Orientações:
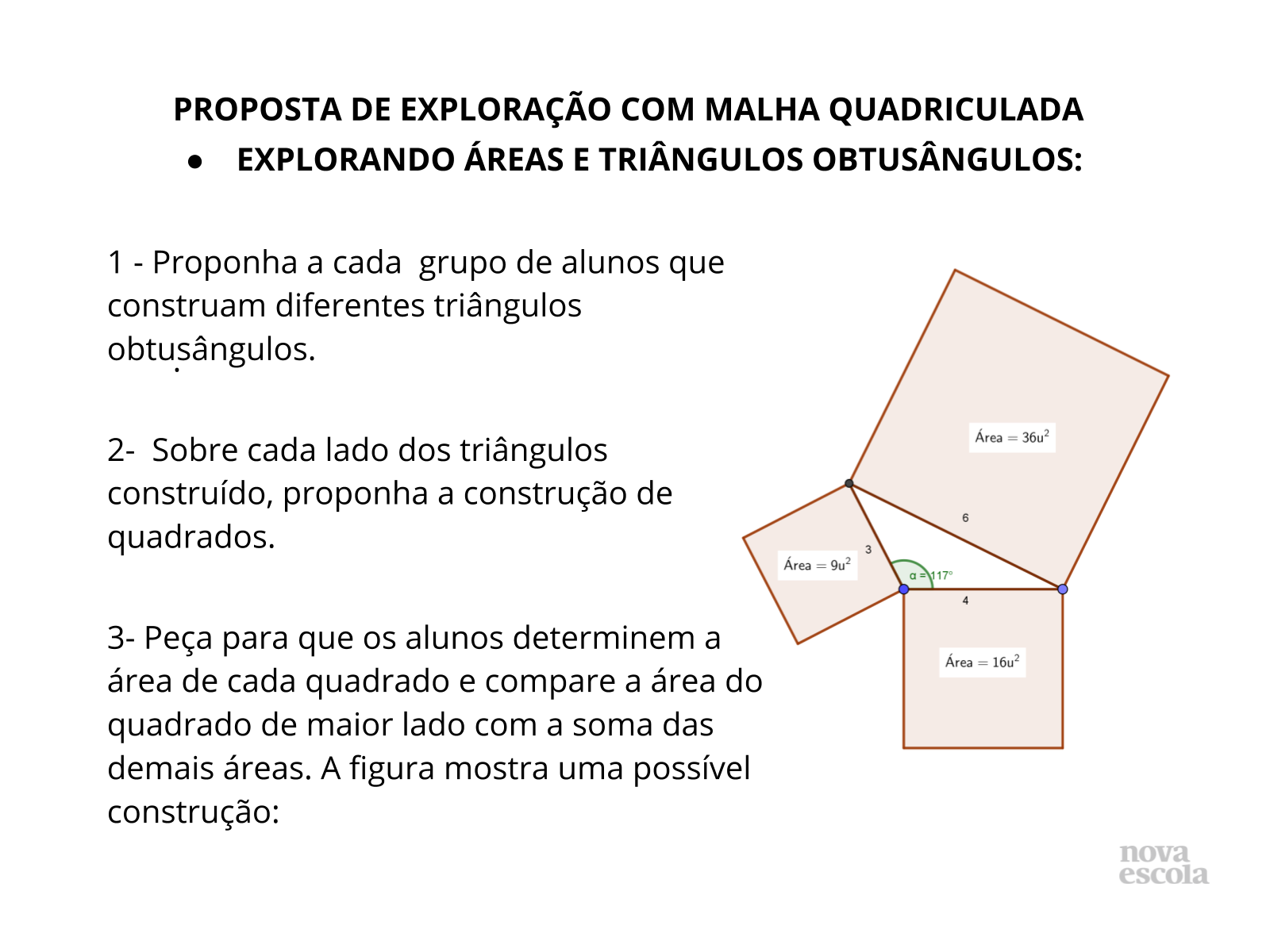
Oriente os alunos na construção dos triângulos. Caso apresentem dificuldades na contagem direta das áreas dos quadrados que ficarem sobre as hipotenusas, proponha o cálculo direto da área pela fórmula A = L², no qual A é a área de um quadrado de lado medindo L unidades.
Propósito: Dar alternativa para o professor realizar a atividade sem o GeoGebra.
Discuta com a turma:
- O que significa comparar dois números?
Atividade Principal
Tempo sugerido: 20 minutos. (slides 9, 10 e 11).
Orientações:
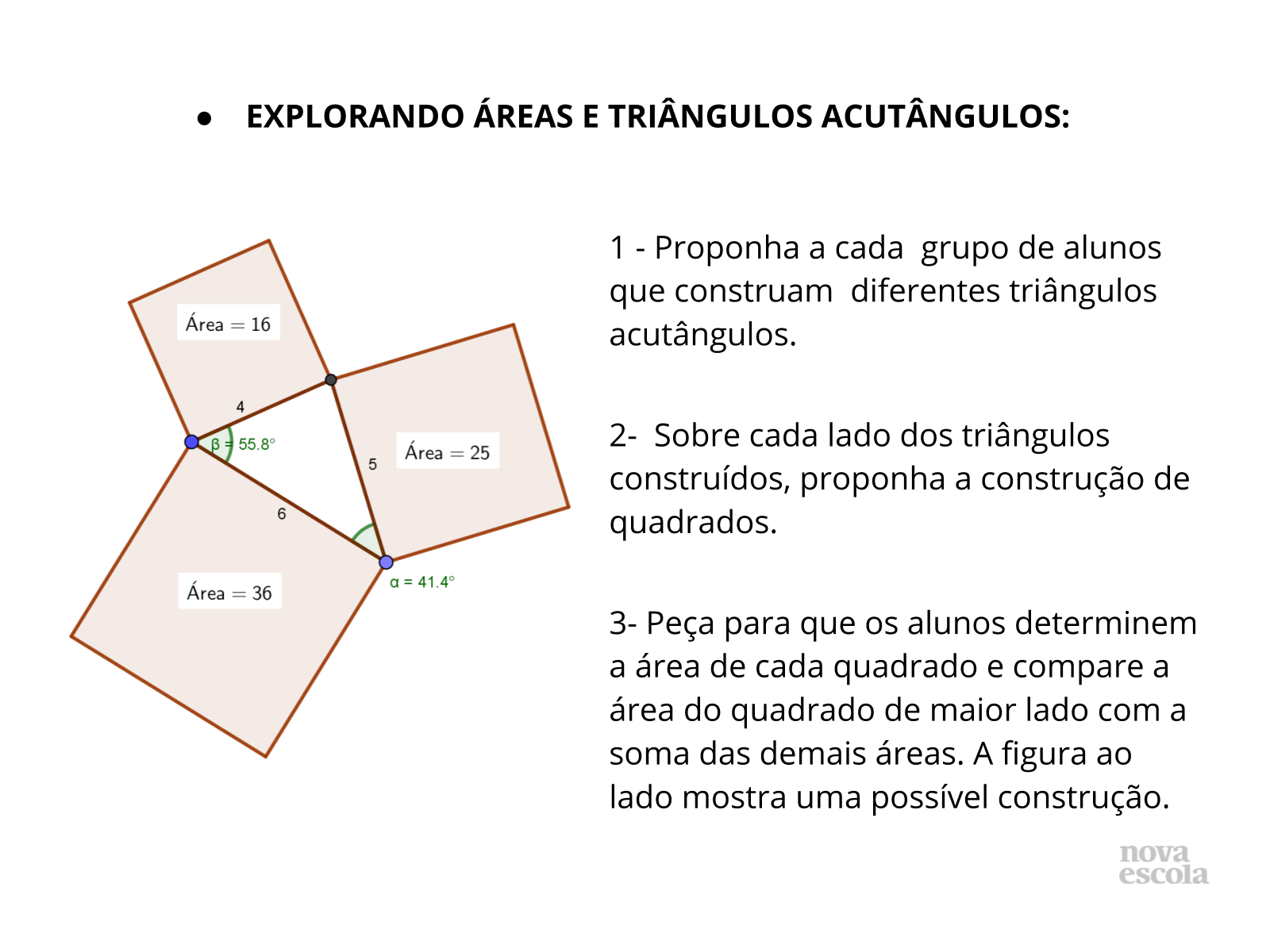
Oriente os alunos na construção dos triângulos. Caso apresentem dificuldades na contagem direta das áreas dos quadrados que ficarem sobre as hipotenusas, proponha o cálculo direto da área pela fórmula A = L², no qual A é a área de um quadrado de lado medindo L unidades.
Propósito: Dar alternativa para o professor realizar a atividade sem o GeoGebra.
Atividade Principal - Opção sem GeoGebra
Título:
Tempo sugerido: 20 minutos (slides 9, 10 e 11).
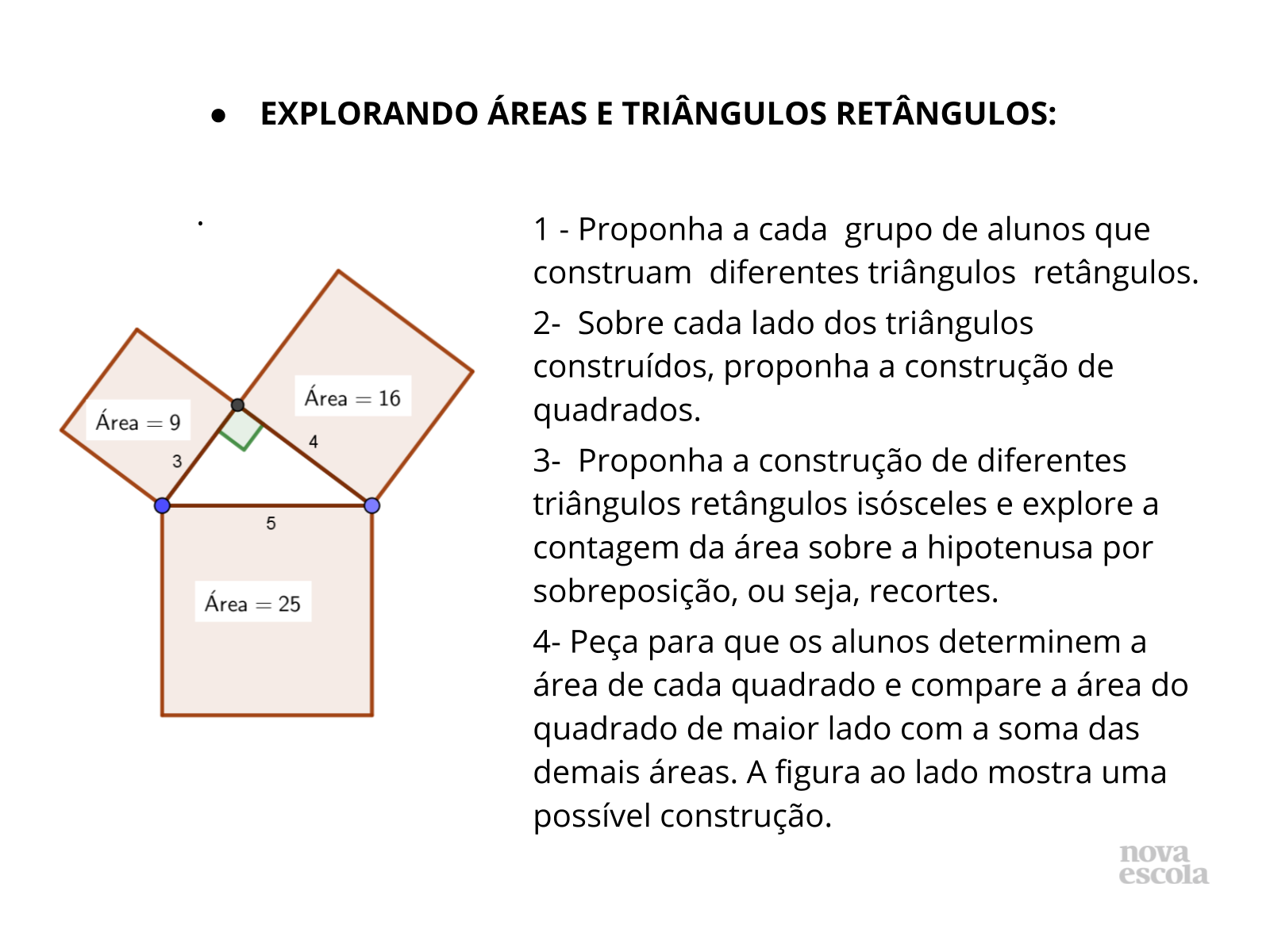
Orientações: Oriente os alunos na construção dos triângulos. Caso apresentem dificuldades na contagem direta das áreas dos quadrados que ficarem sobre as hipotenusas, proponha o cálculo direto da área pela fórmula A = L², no qual A é a área de um quadrado de lado medindo L unidades.
Propósito: Dar alternativa para o professor realizar a atividade sem o GeoGebra.
Discuta com a turma:
- Quando um triângulo é isósceles?
- Entre um triângulo retângulo escaleno e um isósceles, qual apresentou mais facilidade para contagem direta da área? Por quê?
Discussão das Soluções

Tempo sugerido: 5 minutos.
Orientações:
Proponha que a equipe exponha seus resultados para a turma, como forma de conferir a veracidade das relações para triângulos diferentes.
Propósito: Elaboração de tabelas com os dados explorados e exposição à turma.
Discuta com a turma:
- Quando ocorre a igualdade da área do quadrado maior com a soma das áreas dos outros dois quadrados menores?
Sistematização dos Conceitos

Tempo sugerido: 5 minutos.
Orientações:
Proponha que a questão seja resolvida ainda em grupo, como forma de que haja troca de ideias durante a resolução. Se necessário, mostre algum exemplo do cálculo da área de um quadrado de lado dado qualquer.
Propósito: Resolver uma situação problema que requeira a aplicação do conceito explorado na aula.
Discuta com a turma:
- Qual a relação que será aplicada nesta situação?
- É possível determinar a medida da hipotenusa?
Encerramento

Tempo sugerido: 5 minutos.
Orientações:
Sugira que os alunos registrem os resultados alcançados na aula. De modo geral, espera-se que, ao final da aula, apresentem as seguintes conclusões registradas:
Triângulo acutângulo: a² < b²+c²
Triângulo obtusângulo: a² > b²+c²
Triângulo retângulo: a² = b²+c²
Propósito: Generalização do conceito construído na aula: a² = b²+c².
Discuta com a turma:
- Como podemos expressar verbalmente a relação entre as medidas dos lados de um triângulo retângulo?
Raio X
Tempo sugerido: 6 minutos. (slides 15 e 16).
Orientações:
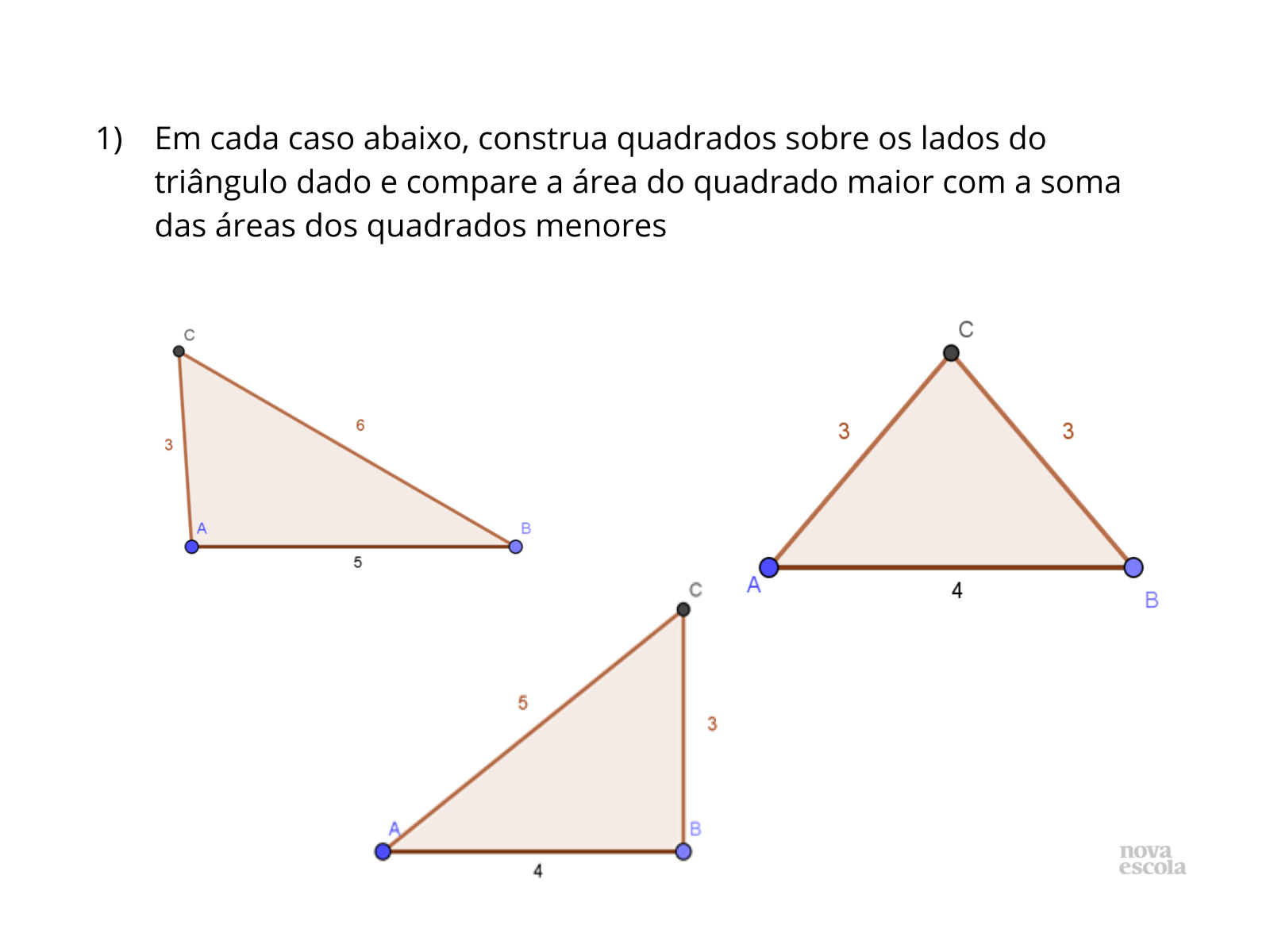
Atividade para verificar a assimilação dos conceitos desenvolvidos em sala de aula. Proponha a resolução individual. Toda as atividades propostas neste Raio - X podem ser adaptadas para a resolução em malha quadriculadas. No entanto, na malha quadriculada o aluno terá que fazer contagem direta, agrupando “pedaços” de quadrados. Outra solução possível é calculando diretamente a área do quadrado sobre a hipotenusa e comparar com a soma das das áreas dos demais quadrados.
Propósito: Verificar se os alunos assimilaram o conceito desenvolvido em aula.
Discuta com a turma:
- Houve alguma dificuldade na resolução desta atividade?
Raio X

Tempo sugerido: 6 minutos. (slides 15 e 16).
Orientações:
Atividade para verificar a assimilação dos conceitos desenvolvidos em sala de aula. Proponha a resolução individual. Toda as atividades propostas neste Raio - X podem ser adaptadas para a resolução em malha quadriculadas. No entanto, na malha quadriculada, o aluno terá que fazer contagem direta, agrupando “pedaços” de quadrados. Outra solução possível é calculando diretamente a área do quadrado sobre a hipotenusa e comparar com a soma das das áreas dos demais quadrados.
Propósito: Verificar se os alunos assimilaram o conceito desenvolvido em aula.
Discuta com a turma:
- Houve alguma dificuldade na resolução desta atividade?
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_15GEO01)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) régua e papel para anotações.
- Optativas: Calculadora e tesoura.
Aquecimento
- Pela rede social escolhida, inicie esse contato questionando se seus alunos e alunas lembram das classificações dos triângulos quanto aos ângulos e lados. Complemente informando todas as definições.
Atividade principal
Faça uso do plano da atividade principal desse plano solicitando que usem o Geogebra (instalado no PC ou online pelo link https://www.geogebra.org/classic?lang=pt_PT) construindo um triângulo qualquer, depois quadrados a partir dos lados dos triângulos e os ângulos internos do triângulo.
Se ainda houver necessidade de algum estudante no manuseio do Geogebra, repasse o passo-a-passo contido no plano original, após, peça a todos que façam todos os movimentos previstos nele para fazer a discussão da exploração.
Discussão das soluções
- Na discussão das soluções, peça que alguns compartilhem seus resultados para que sirvam de comparação com os outros.
Sistematização e encerramento
- Faça uma sistematização destacando que a relação do teorema de Pitágoras serve apenas ao triângulo e que nos outros casos acontecem desigualdades:
Triângulo acutângulo: a² < b²+c²
Triângulo obtusângulo: a² > b²+c²
Triângulo retângulo: a² = b²+c²
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e relatem suas explorações sobre os desenhos e links.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Sebastiao Rodrigues da Silva
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
(EF09MA14) Resolver e elaborar problemas de aplicação do Teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
Objetivos específicos
Identificar o triângulo retângulo como o caso em que ocorre a igualdade da soma das áreas menores com a área sobre o lado maior (Hipotenusa)
Conceito-chave
Exploração intuitiva do Teorema de Pitágoras.
Recursos necessários
- Computador
- Software GeoGebra
- Projetor
- Lápis, régua e compasso
- Malha quadriculada
- Atividades impressas