Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “S
obre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 6 minutos.
Orientações: Faça à turma uma pergunta por vez e deixe que todos comentem o que lembram a respeito ou o que acreditam que seja um exemplo de semelhança no dia a dia.
Propósito: Retomar o conceito de semelhança de figuras e verificar a aplicabilidade deste conceito por meio de contextos que ele pode estar inserido.
Discuta com a turma:
- Em relação à primeira pergunta, podem surgir respostas como: é quando as figuras são parecidas mas têm tamanhos diferentes. Certifique-se que os alunos recordem que figuras são semelhantes sempre que uma puder ser transformada na outra por meio de uma ampliação, redução ou a partir de um movimento rígido (translação, rotação ou reflexão). Dessa forma, triângulos com o mesmo tamanho (congruentes) também são semelhantes.
Se nenhum aluno lembrar que, para figuras serem semelhantes é necessário que os ângulos correspondentes sejam congruentes e os lados correspondentes proporcionais, questione-os:
- Figuras semelhantes podem ter ou não o mesmo tamanho, certo?
- Quais são as partes que compõem uma figura geométrica?
- Quais destas partes pode ter relação com a semelhança?
- O que pode garantir que as duas sejam parecidas?
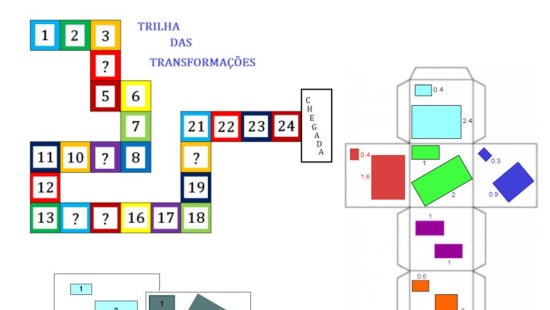
Aquecimento
Resolução do Aquecimento
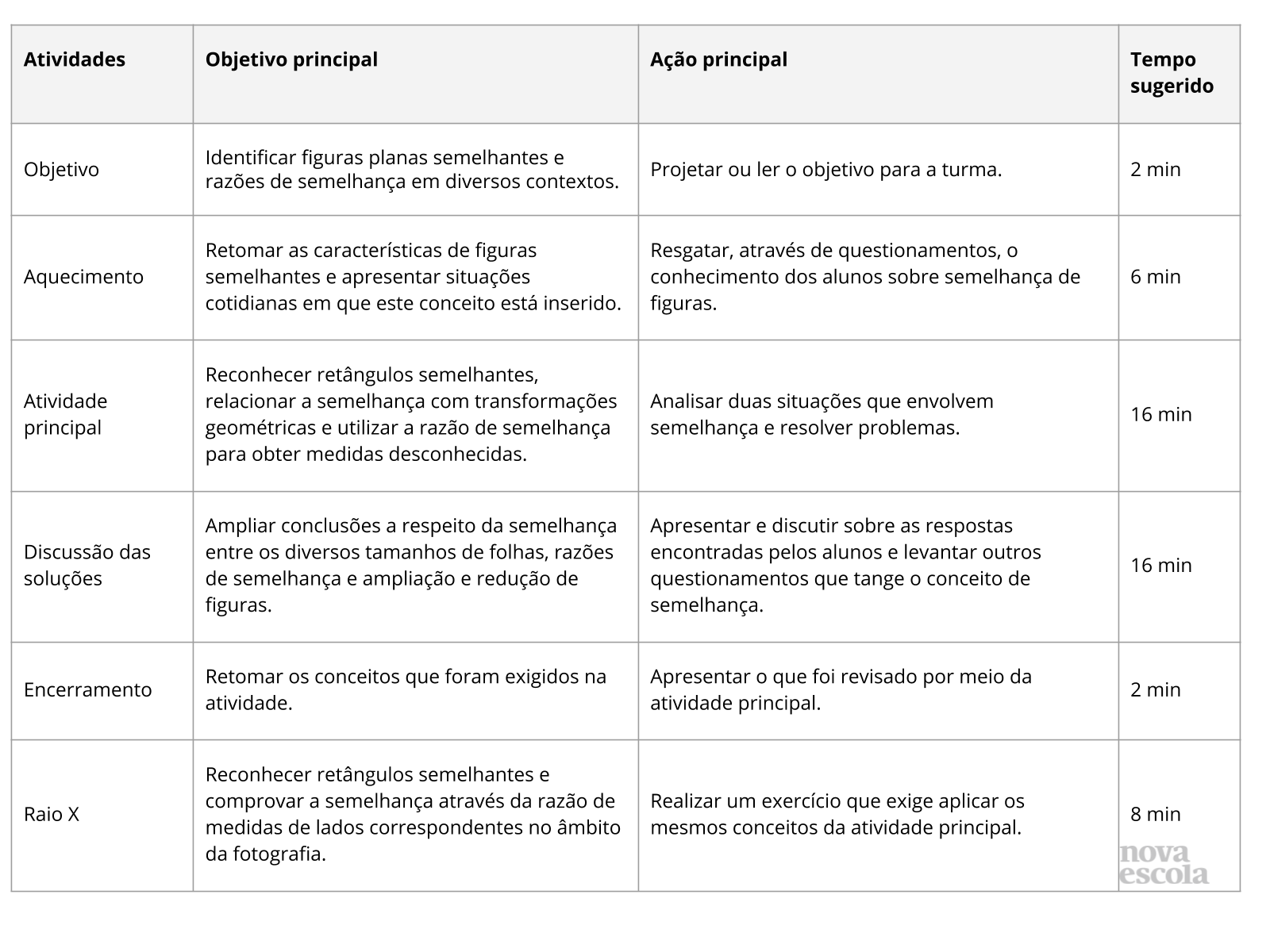
Atividade Principal

Tempo sugerido: 16 minutos (slides 4, 5, 6 e 7) .
Orientações: Peça que, individualmente, os alunos leiam a atividade para responderem os itens solicitados.
Propósito: Identificar figuras semelhantes através do cálculo de razões entre lados correspondentes e reconhecer as transformações por homotetia (ampliação e redução).
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal
Tempo sugerido: 16 minutos (slides 4, 5, 6 e 7) .
Orientações: Peça que, individualmente, os alunos leiam a atividade para responderem os itens solicitados.
Propósito: Identificar figuras semelhantes através do cálculo de razões entre lados correspondentes e reconhecer as transformações por homotetia (ampliação e redução).
Materiais complementares:
Atividade principal para impressão
Resolução da atividade principal
Guia de intervenção
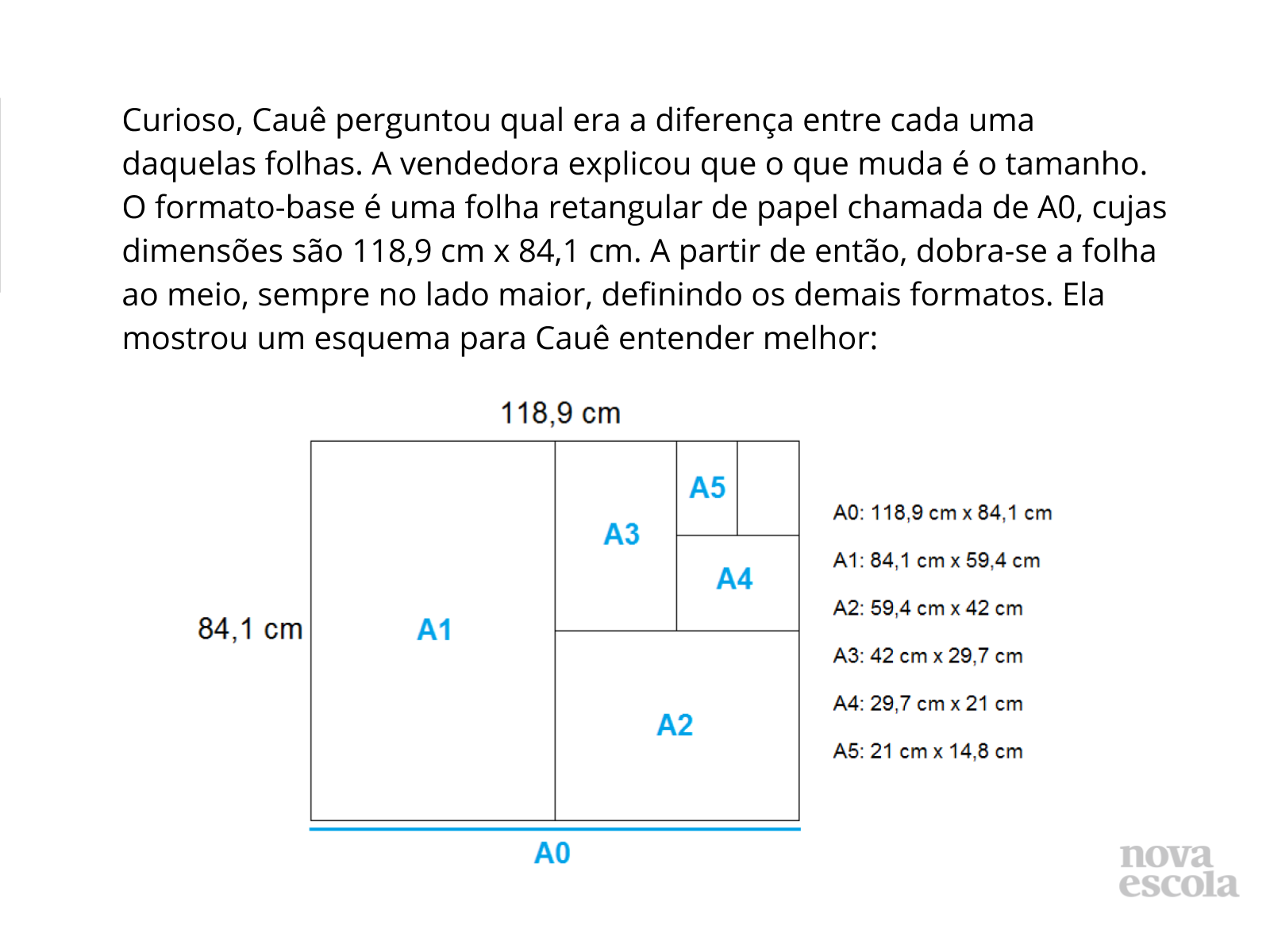
Atividade Principal

Tempo sugerido: 16 minutos (slides 4, 5, 6 e 7) .
Orientações: Peça que os alunos analisem o esquema dos tamanhos das folhas e respondam aos itens solicitados.
Propósito: Identificar figuras semelhantes através do cálculo de razões entre lados correspondentes e reconhecer as transformações por homotetia (ampliação e redução).
Materiais complementares:
Atividade principal para impressão
Resolução da atividade principal
Guia de intervenção
Atividade Principal
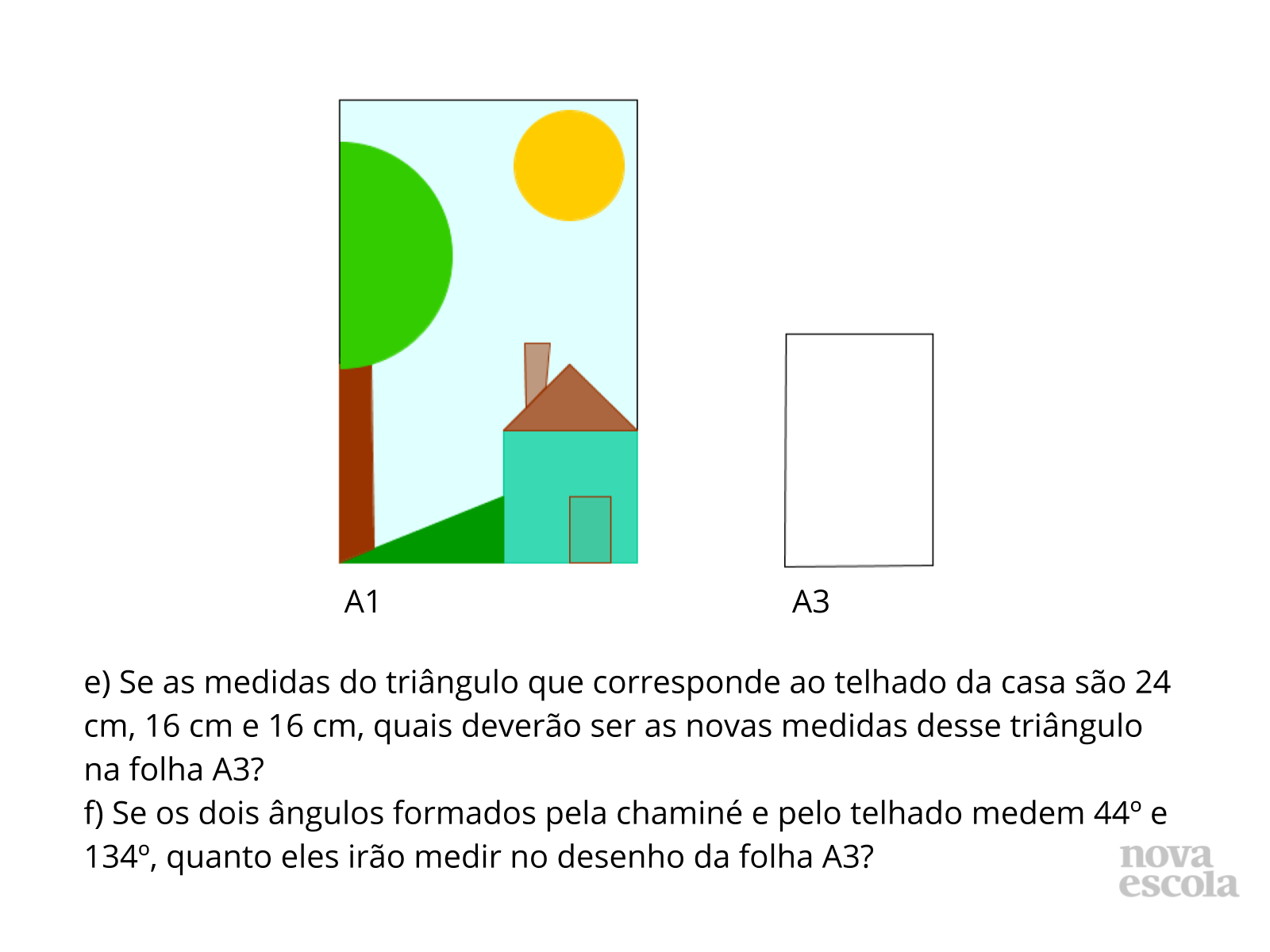
Tempo sugerido: 16 minutos (slides 4, 5, 6 e 7) .
Orientações: Certifique-se que os alunos compreenderam esta parte da atividade. Circule na sala a fim de verificar se os alunos estão com dificuldades de elaborar uma estratégia para responder estes itens. Você pode sugerir também que os alunos se reúnam em duplas para discutirem o que já pensaram e juntos elaborarem uma estratégia.
Propósito: Retomar características de figuras semelhantes e utilizar a razão de semelhança para obter medidas de figuras semelhantes.
Discuta com a turma:
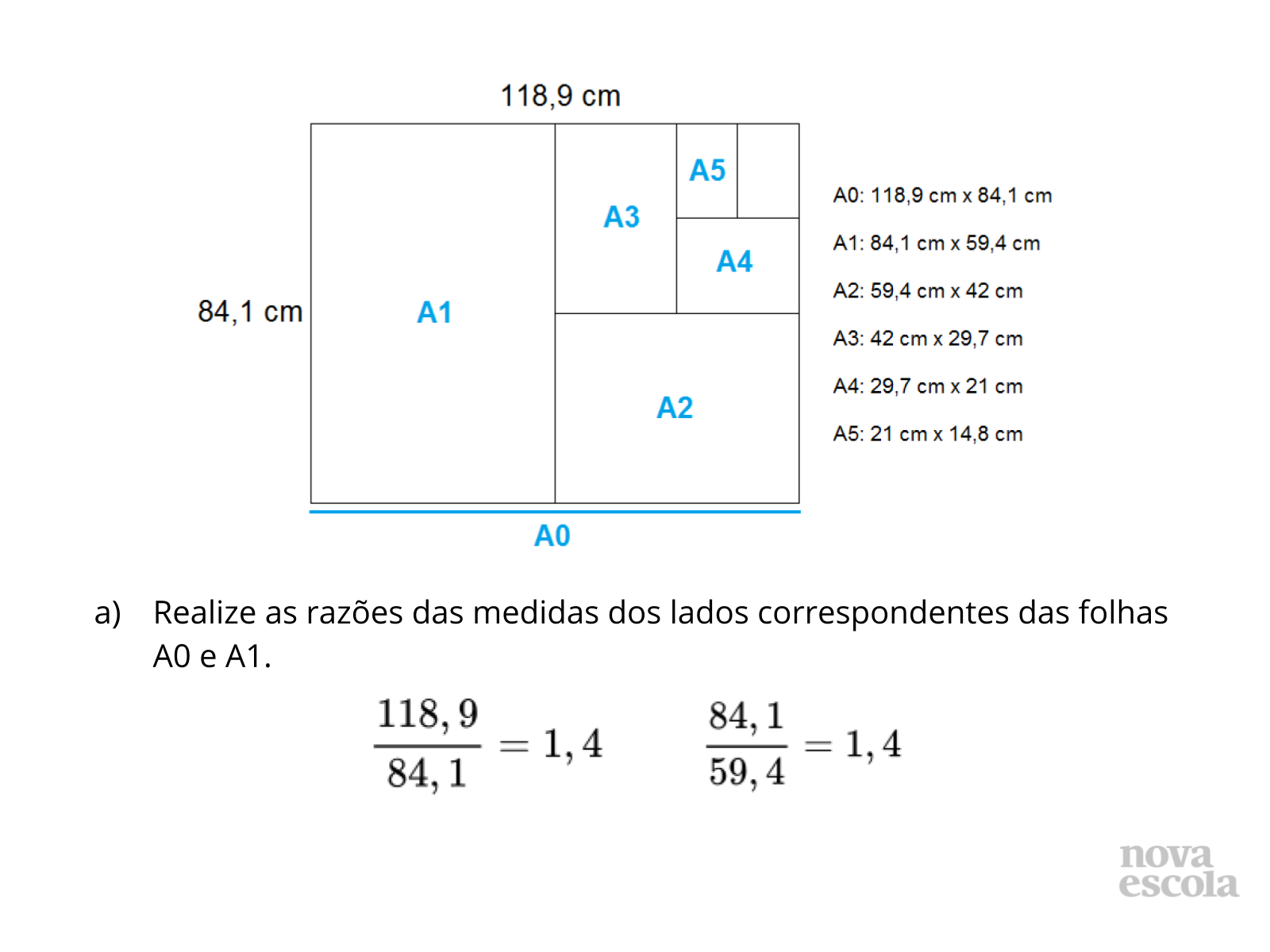
- As folhas A3 e A1 são semelhantes?
- Qual informação possibilita calcular medidas desconhecidas de figuras semelhantes?
- Essa informação está explícita no problema? Essa informação já foi ou pode ser calculada?
Materiais complementares:
Atividade principal para impressão
Resolução da atividade principal
Guia de intervenção
Discussão da Solução
Título:
Tempo sugerido: 16 minutos (slides 8, 9, 10 e 11) .
Orientações: Convide alguns alunos a exporem seus resultados. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos.
Propósito: Discutir com os alunos as respostas obtidas e retomar conceitos que se referem à semelhança de retângulos e triângulos.
Discuta com a turma:
- O que acontece se invertermos as razões?
Discussão da Solução

Título:
Tempo sugerido: 16 minutos (slides 8, 9, 10 e 11) .
Orientações: Convide alguns alunos a exporem seus resultados. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos.
Propósito: Discutir com os alunos as respostas obtidas e retomar conceitos que se referem à semelhança de retângulos e triângulos.
Discuta com a turma:
- O que podemos afirmar quando as razões das medidas de todos os lados correspondentes das figuras são iguais?
- Qual(is) outra(s) característica(s) podemos observar nas folhas A0 e A1 que as tornam semelhantes?
- Além de todos os pares de folhas que vocês comprovaram serem semelhantes, existe ainda mais pares semelhantes?
Discussão da Solução
Título:
Tempo sugerido: 16 minutos (slides 8, 9, 10 e 11) .
Orientações: Convide alguns alunos a exporem seus resultados. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos.
Propósito: Discutir com os alunos as respostas obtidas e retomar conceitos que se referem à semelhança de retângulos e triângulos.
Discuta com a turma:
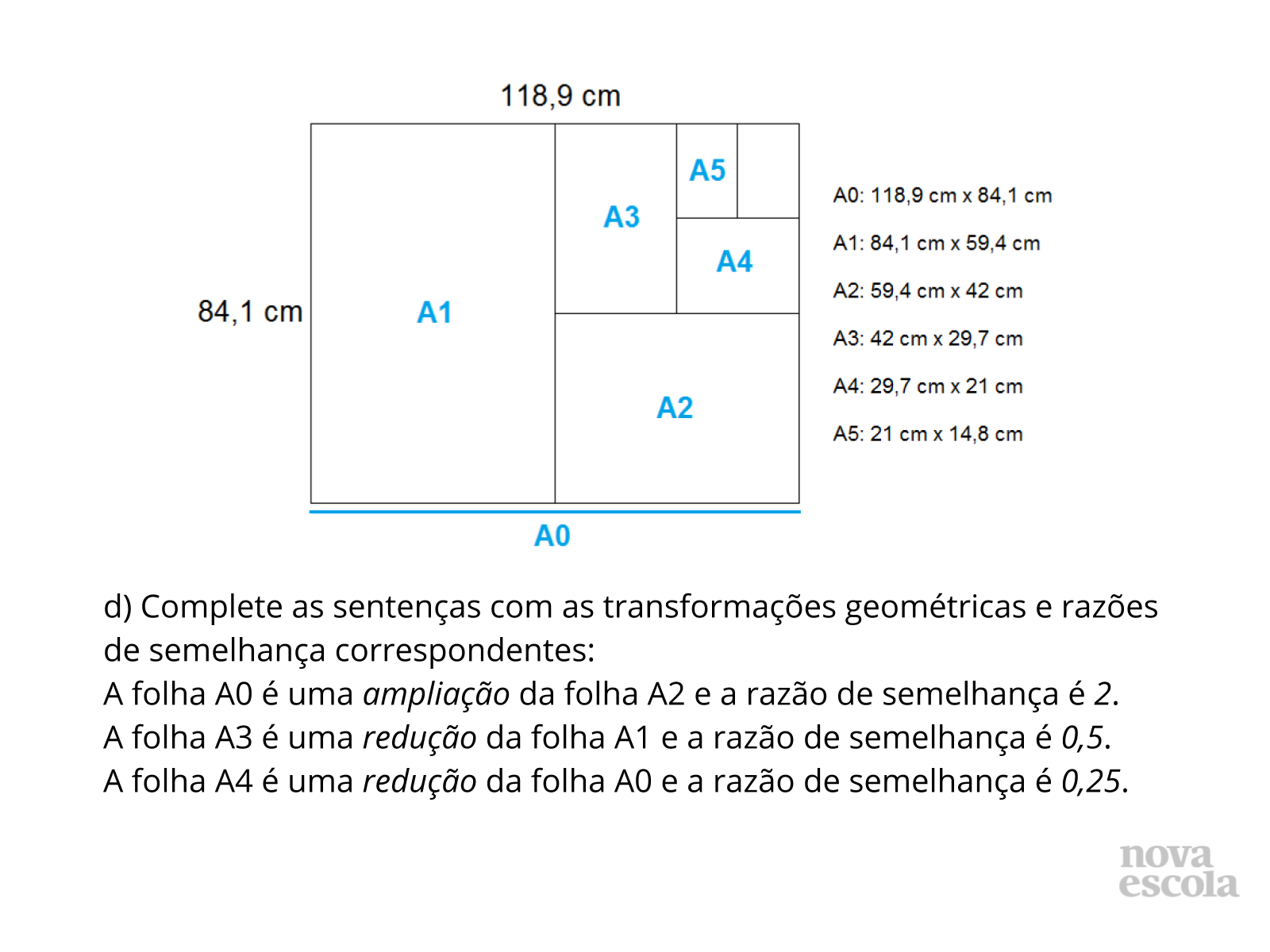
- Se invertermos as folhas que estão sendo comparadas, o que podemos afirmar sobre a transformação geométrica utilizada?
- Como é a razão de semelhança quando é realizada uma ampliação? E quando for uma redução?
Discussão da Solução
Título:
Tempo sugerido: 16 minutos (slides 8, 9, 10 e 11) .
Orientações: Convide alguns alunos a exporem seus resultados. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos.
Propósito: Discutir com os alunos as respostas obtidas e retomar conceitos que se referem à semelhança de retângulos e triângulos.
Discuta com a turma:
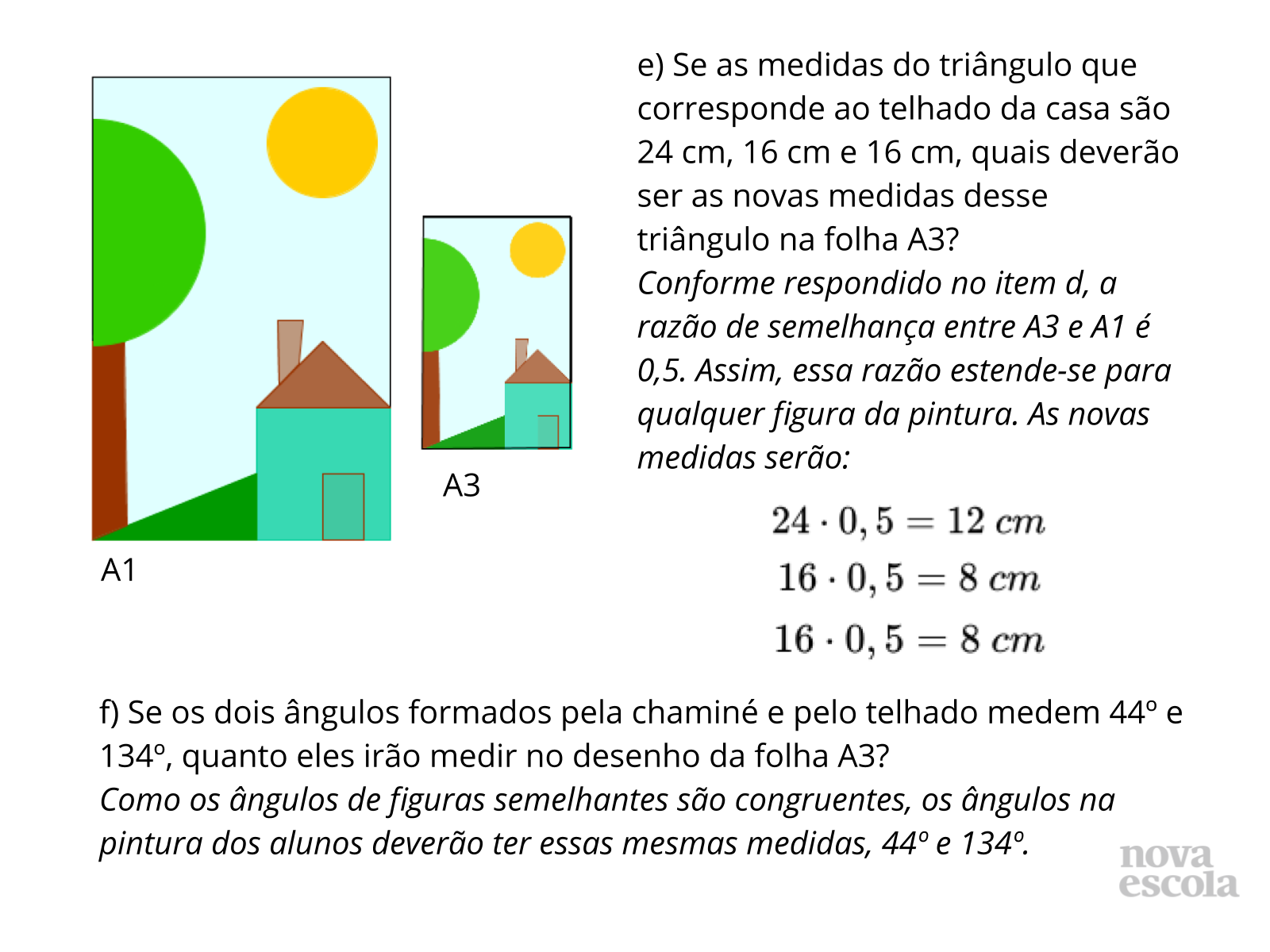
- Por que podemos afirmar que a razão de semelhança entre as folhas é válida também para as figuras presentes na pintura?
- Vocês podem citar algum exemplo real, que se assemelhe à realização da redução da pintura?
- Além de multiplicar as medidas do triângulo por 0,5, é possível obter os mesmos resultados realizando outra operação?
- Por que dividir por dois é equivalente a multiplicar por 0,5?
- O que acontece com os ângulos de uma figura quando esta é ampliada? E quando é reduzida?
Encerramento
Título:
Tempo sugerido: 2 minutos.
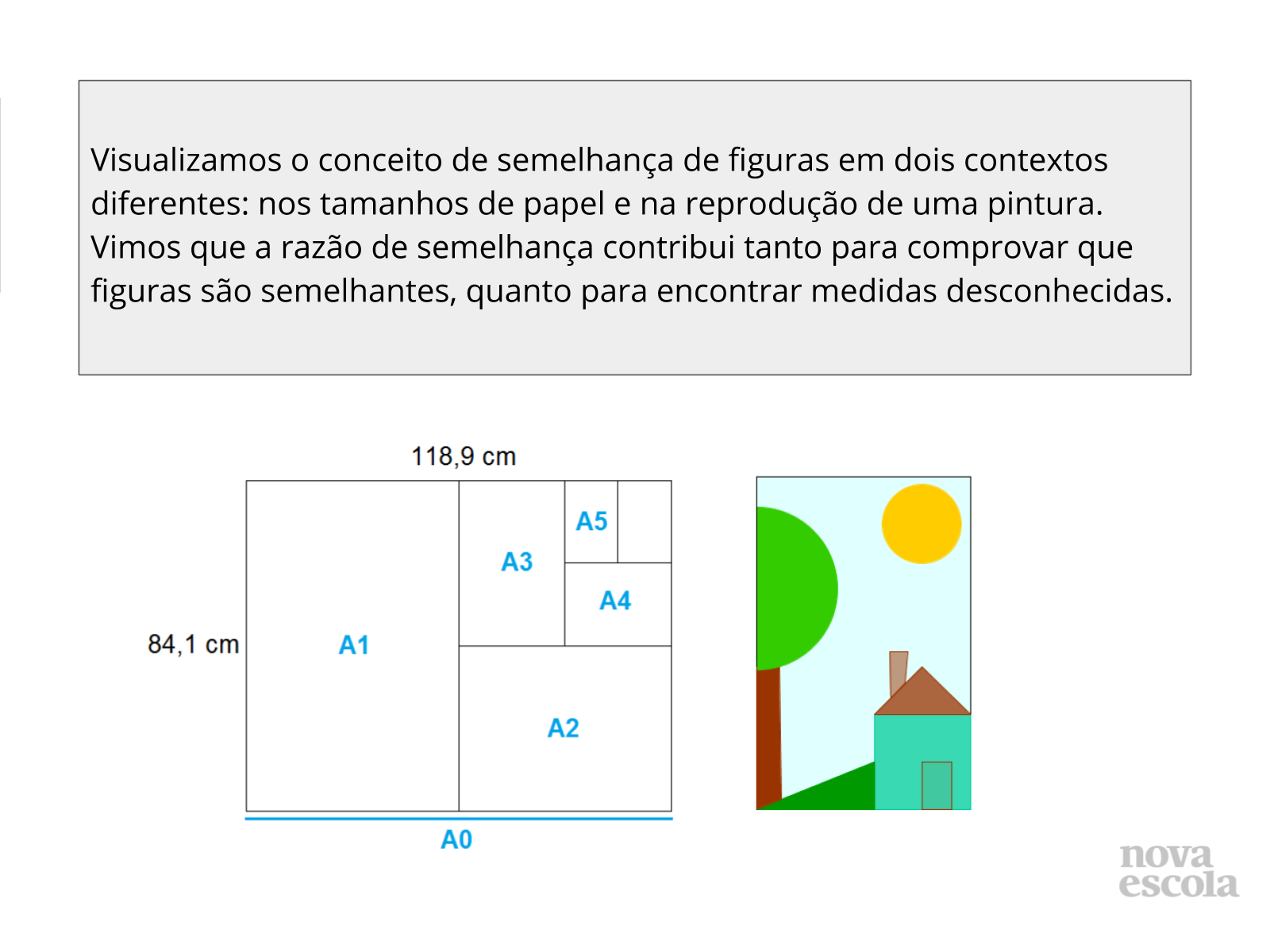
Orientações: Encerre a atividade retomando com os estudantes os contextos em que a semelhança de figuras apareceu. Peça que leiam a conclusão e registrem no caderno a respeito da importância da razão de semelhança.
Propósito: Retomar os conceitos envolvidos na atividade principal.
Raio X
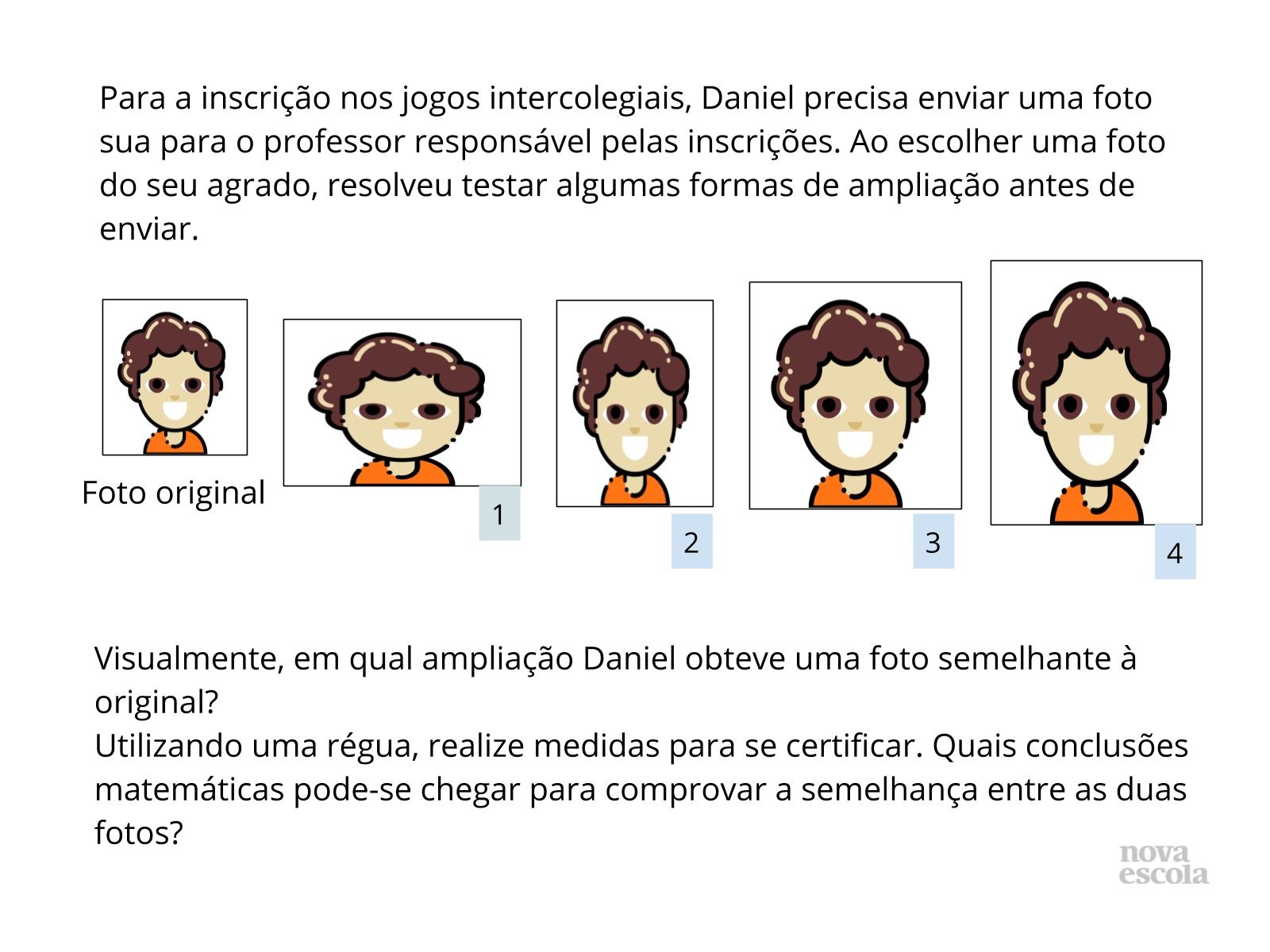
Tempo sugerido: 8 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo, registrando as soluções na lousa.
Propósito: Auxiliar os alunos a perceberem que nem toda a ampliação de uma figura é semelhante à figura original. É necessário sempre manter as características da figura e verificar matematicamente a semelhança.
Discuta com a turma:
- Por que algumas ampliações não se assemelham à foto original?
- Se Daniel utilizou algum programa de edição de fotos para fazer as ampliações, como será que ele fez para que a ampliação não fosse semelhante à foto original? E como será que ele procedeu para que a ampliação ficasse semelhante?
Materiais complementares:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar