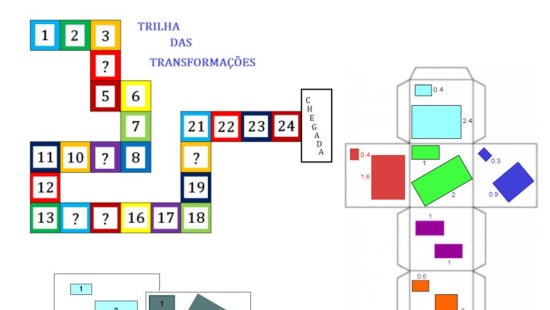
Atividade principal
Plano de Aula
Plano de aula: Os Retângulos dos Vitrais
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Semelhança de figuras planas e transformações no espaço.
Por: Eduardo Post
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Eduardo Post
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
Relacionada a EF09MA12 - Reconhecer as condições necessárias e suficientes para que dois triângulos sejam semelhantes.
Objetivos específicos
- Compreender o que é semelhança de retângulos.
- Identificar/calcular a razão de semelhança.
- Relacionar a semelhança entre retângulos e movimentos de transformações no espaço.
Conceito-chave
Razão de semelhança em retângulos.
Recursos necessários
Lápis de colorir, vitrais impressos (malha quadriculada) e régua.
Vocabulário que será adquirido nesta aula
Semelhança entre retângulos, razão de semelhança, ampliação, redução.
Habilidades BNCC:
Objetivos de aprendizagem
- Compreender o que é semelhança de retângulos.
- Identificar/calcular a razão de semelhança.
- Relacionar a semelhança entre retângulos e movimentos de transformações no espaço.
Resumo da aula
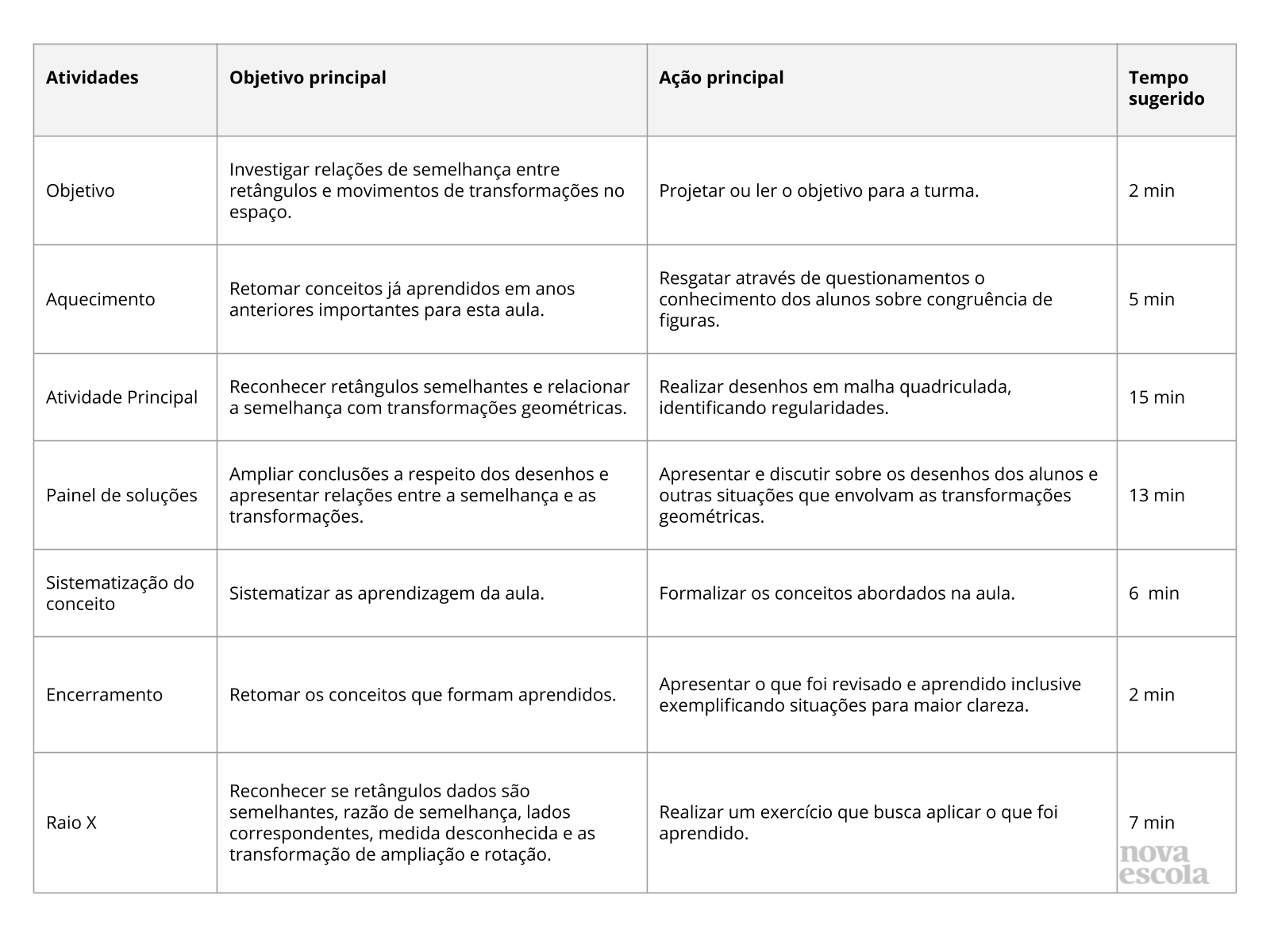
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 5 minutos.
Orientações: Faça à turma uma pergunta por vez e deixe que todos comentem o que lembram a respeito.
Propósito: Retomar o conceito de congruência de figuras para facilitar posteriormente a compreensão do conceito de semelhança e chegar a conclusão de que toda figura congruente é também semelhante.
Discuta com a turma:
- Em relação à primeira pergunta, podem surgir respostas como: “é quando as figuras têm o mesmo tamanho e forma” ou “é quando as figuras são iguais”.
- Garanta que os alunos compreendam a noção intuitiva de congruência: duas figuras são congruentes se, ao transportar uma sobre a outra, elas coincidem.
Atividade Principal

Tempo sugerido: 15 minutos (slides 3, 4, 5, e 6).
Orientações: Peça que, individualmente, os alunos leiam a atividade e realizem os desenhos dos retângulos utilizando régua. Os alunos podem ter dificuldade de reduzir os lados do retângulo à metade pois precisarão encontrar o ponto médio de um dos quadradinhos da malha. Fique atento aos comentários dos alunos para auxiliá-los se for preciso. Circule na sala para verificar se os alunos não têm dúvidas a respeito do que fazer ou se necessitam auxílio na construção das semirretas. O retângulo original será o ABCD e os retângulos desenhados pelos alunos serão representados por A’B’C’D’. Deixe que comparem seus desenhos com um colega e identifiquem as diferenças e semelhanças. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
Propósito: Identificar o ponto de interseção das semirretas nos retângulos dos itens a e b e identificar regularidades nos segmentos determinados pelos vértices e este ponto.
Materiais complementares:
Atividade Principal
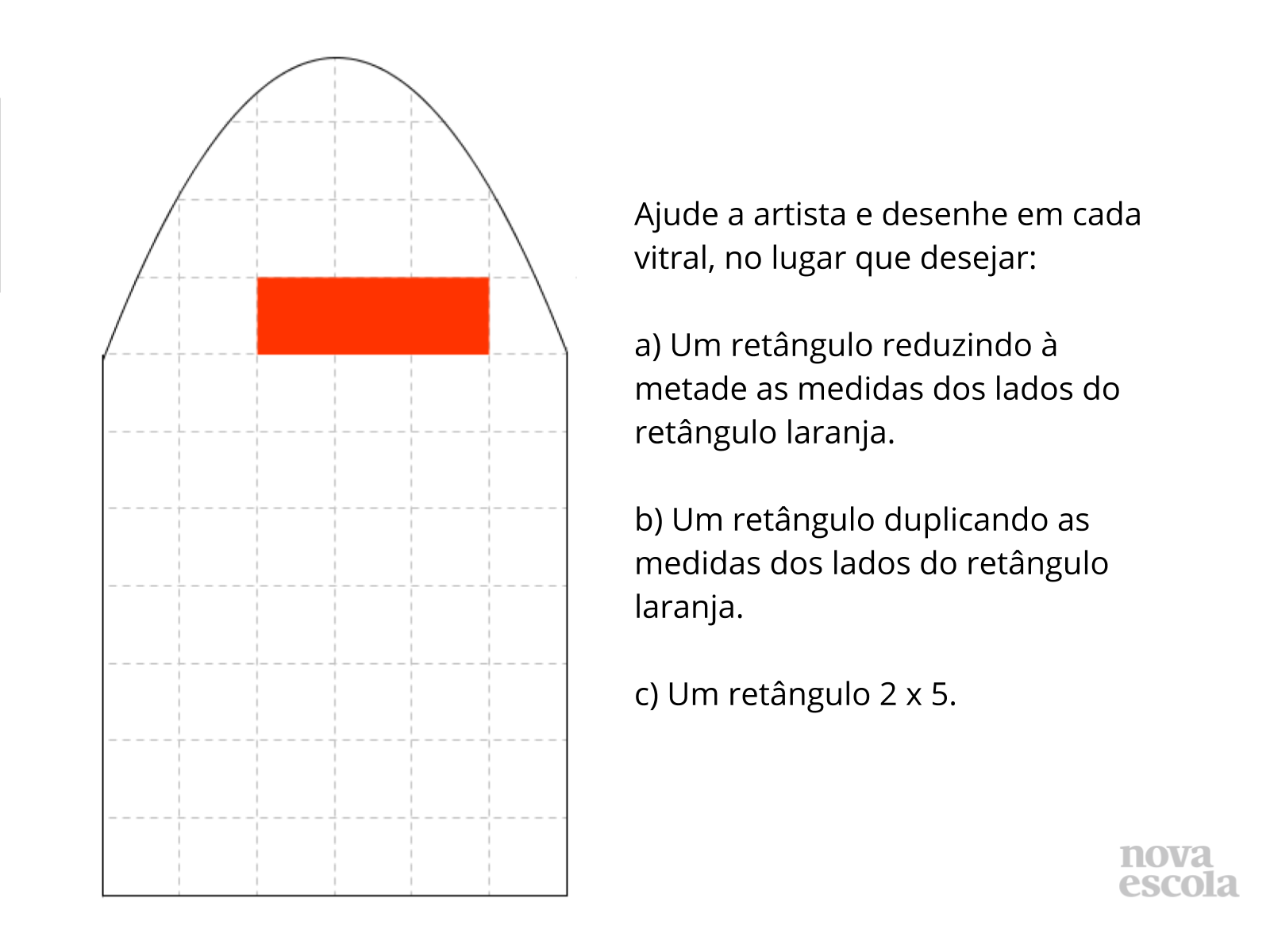
Tempo sugerido: 15 minutos (slides 3, 4, 5, e 6).
Orientações: Peça que, individualmente, os alunos leiam a atividade e realizem os desenhos dos retângulos utilizando régua. Os alunos podem ter dificuldade de reduzir os lados do retângulo à metade pois precisarão encontrar o ponto médio de um dos quadradinhos da malha. Fique atento aos comentários dos alunos para auxiliá-los se for preciso. Circule na sala para verificar se os alunos não têm dúvidas a respeito do que fazer ou se necessitam auxílio na construção das semirretas. O retângulo original será o ABCD e os retângulos desenhados pelos alunos serão representados por A’B’C’D’. Deixe que comparem seus desenhos com um colega e identifiquem as diferenças e semelhanças. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
Propósito: Identificar o ponto de interseção das semirretas nos retângulos dos itens a e b e identificar regularidades nos segmentos determinados pelos vértices e este ponto.
Materiais complementares:
Atividade principal para impressão
Atividade Principal
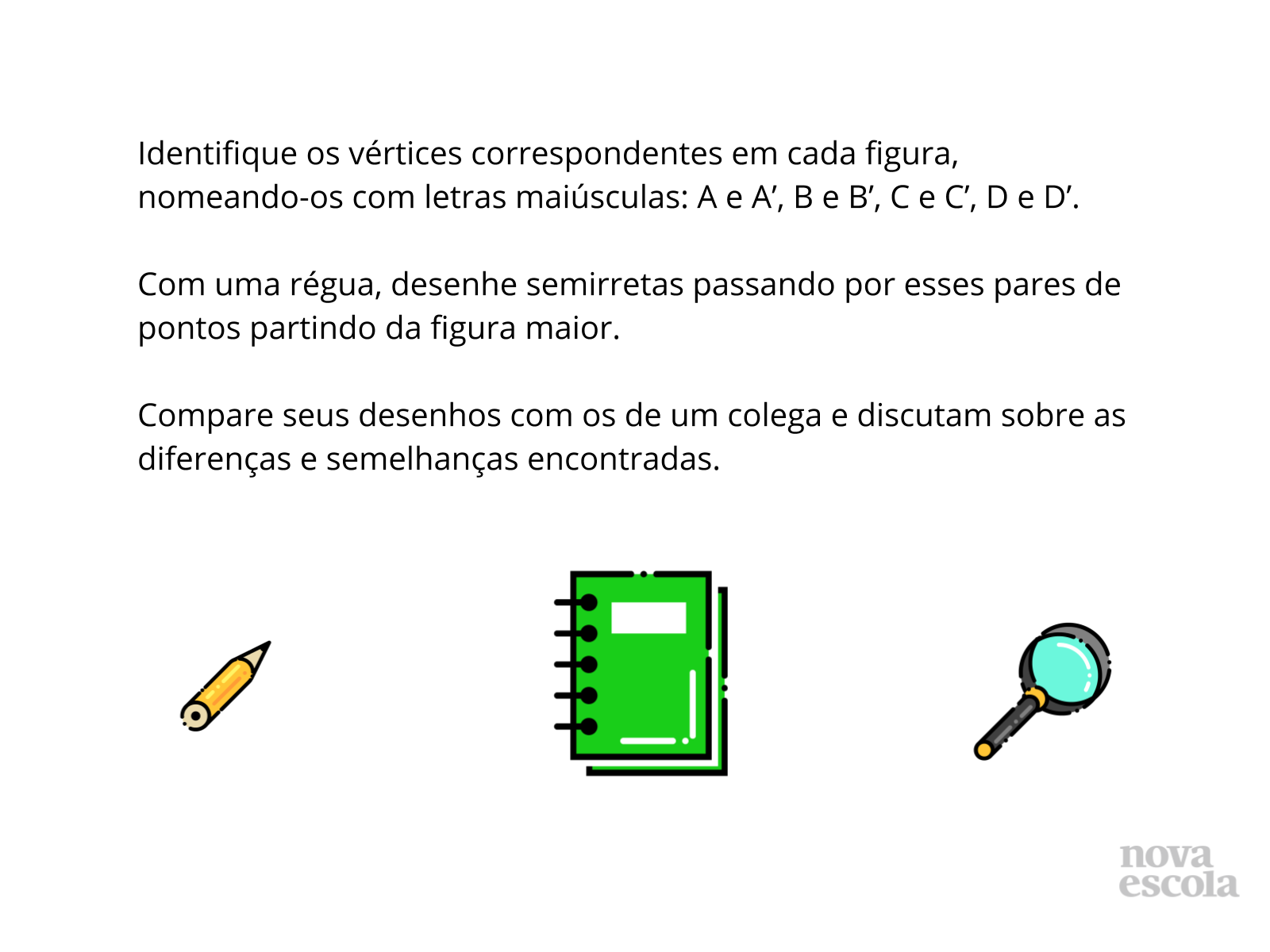
Tempo sugerido: 15 minutos (slides 3, 4, 5, e 6).
Orientações: Peça que, individualmente, os alunos leiam a atividade e realizem os desenhos dos retângulos utilizando régua. Os alunos podem ter dificuldade de reduzir os lados do retângulo à metade pois precisarão encontrar o ponto médio de um dos quadradinhos da malha. Fique atento aos comentários dos alunos para auxiliá-los se for preciso. Circule na sala para verificar se os alunos não têm dúvidas a respeito do que fazer ou se necessitam auxílio na construção das semirretas. O retângulo original será o ABCD e os retângulos desenhados pelos alunos serão representados por A’B’C’D’. Deixe que comparem seus desenhos com um colega e identifiquem as diferenças e semelhanças. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
Propósito: Identificar o ponto de interseção das semirretas nos retângulos dos itens a e b e identificar regularidades nos segmentos determinados pelos vértices e este ponto.
Materiais complementares:
Atividade principal para impressão
Discussão da solução
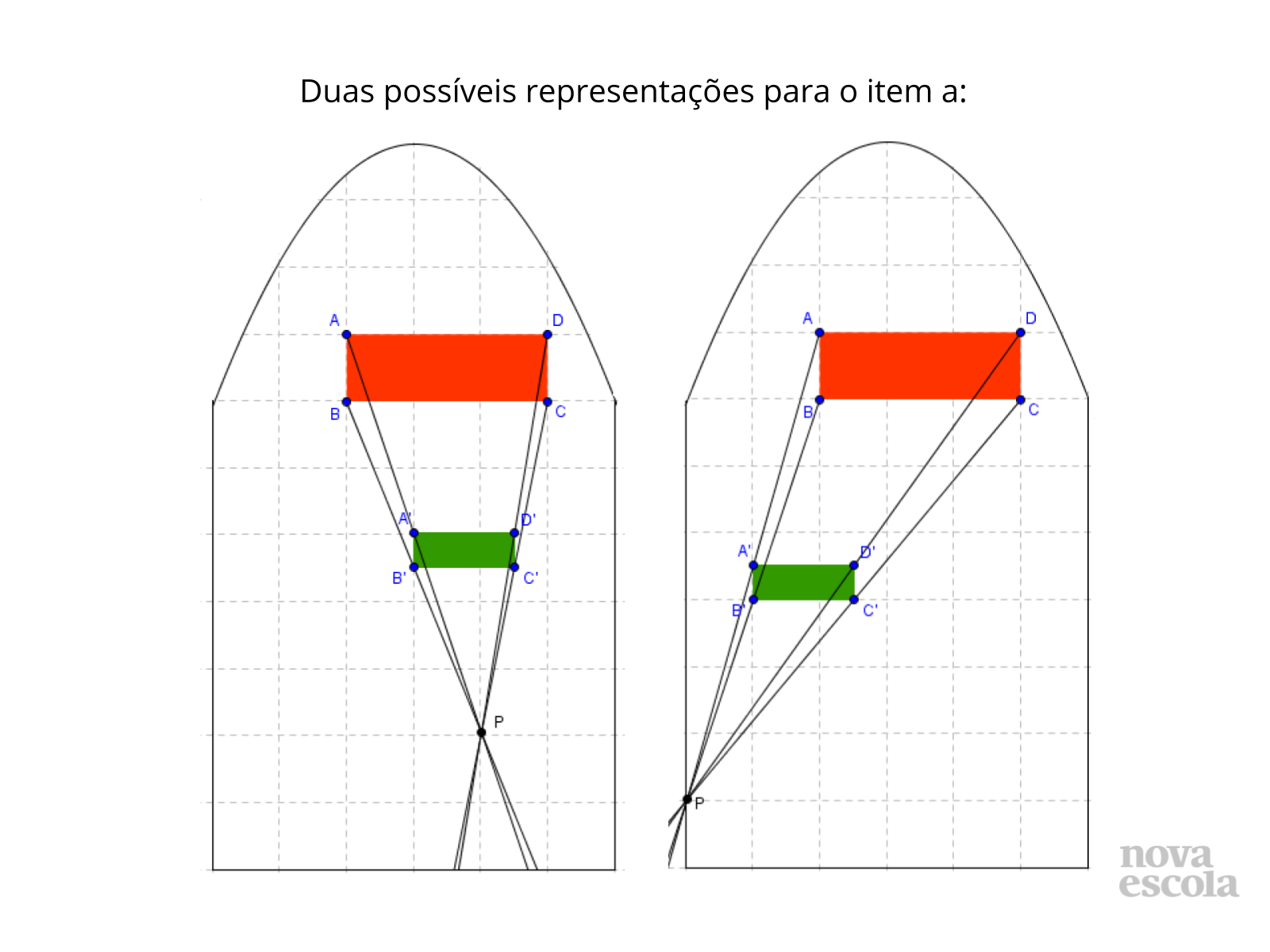
Tempo sugerido: 13 minutos (slides 7, 8, 9, 10 e 11).
Orientações: Para essa discussão você pode utilizar 2 ou 3 desenhos dos próprios alunos de cada item solicitado. Os alunos, juntamente com você, vão chegando a conclusões a respeito das características de retângulos semelhantes. Vão perceber que a ampliação ou redução de uma figura é semelhante à original quando esta, possui os ângulos correspondentes congruentes e os lados proporcionais. Durante as discussões da solução, aborde figuras nos vitrais que sofreram transformações isométricas: reflexão, rotação e translação para que os alunos percebam, que nesse tipo de transformação, o tamanho se mantém, ou seja, os retângulos são congruentes e esse é também um tipo de semelhança.
Propósito: Fazer com que os alunos percebam que as semirretas nos retângulos semelhantes se interceptam no mesmo ponto. Chame esse ponto de P e conjecture com os alunos. PA = 2PA’ e o mesmo ocorre nos outros vértices. O fator 2 é que vai determinar a razão de semelhança.
Discuta com a turma:
- O que acontece com as medidas dos segmentos PA e PA’? O mesmo ocorre com os segmentos que passam pelos outros vértices?
- Por que será que isso ocorre?
- Por que no retângulo 2 x 5 as semirretas não se interceptam no mesmo ponto? Qual a diferença em relação aos outros dois?
- Como são os lados das figuras que possuem o ponto P? E os ângulos?
- O que acontece se dividirmos a medida de cada lado do retângulo desenhado por vocês pela medida do lado correspondente do retângulo da artista?
- Para retângulos serem semelhantes, é suficiente os ângulos serem congruentes? Justifique.
Discussão da solução
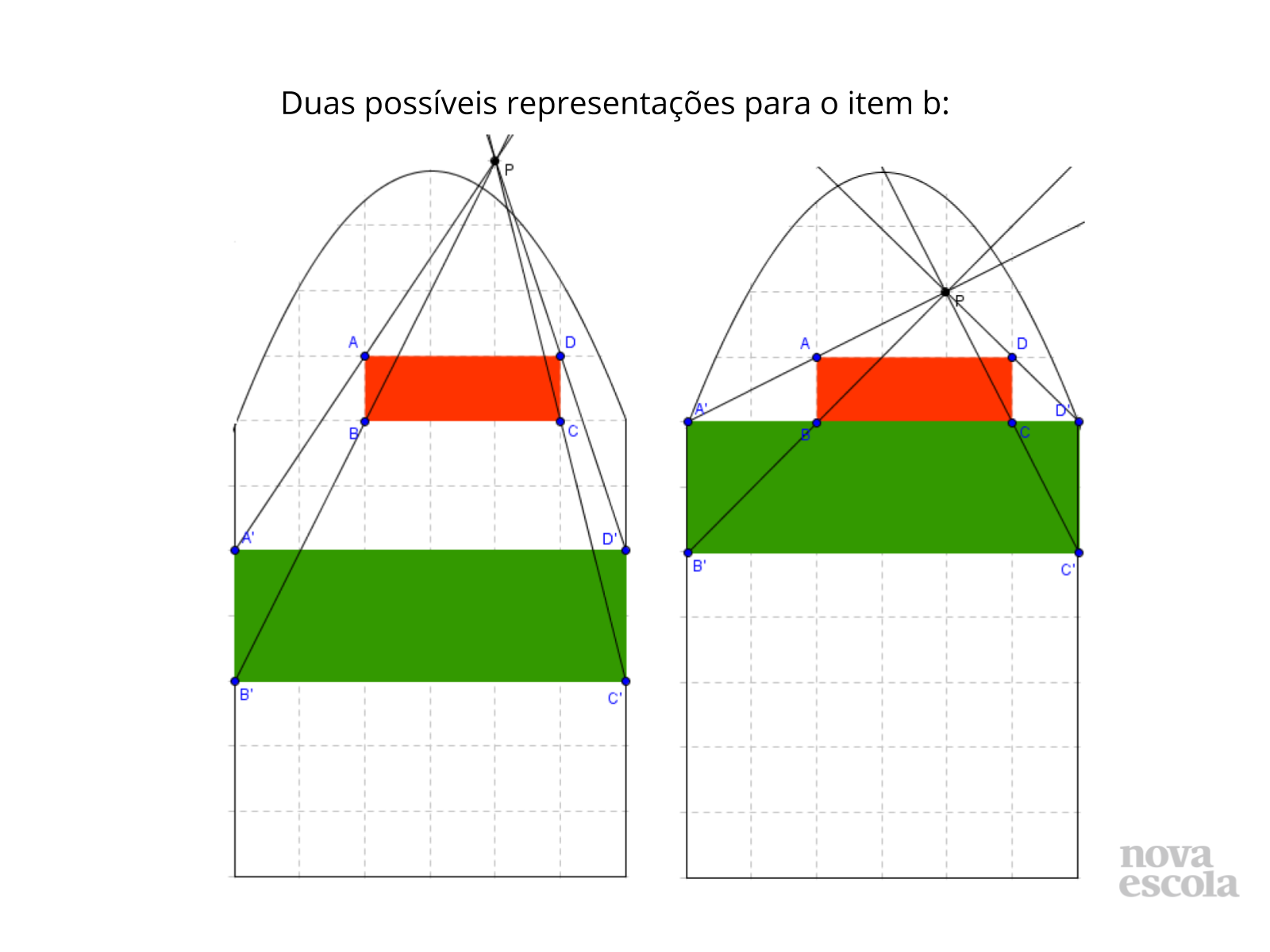
Tempo sugerido: 13 minutos (slides 7, 8, 9, 10 e 11).
Orientações: Para essa discussão você pode utilizar 2 ou 3 desenhos dos próprios alunos de cada item solicitado. Os alunos, juntamente com você, vão chegando a conclusões a respeito das características de retângulos semelhantes. Vão perceber que a ampliação ou redução de uma figura é semelhante à original quando esta, possui os ângulos correspondentes congruentes e os lados proporcionais. Durante as discussões da solução, aborde figuras nos vitrais que sofreram transformações isométricas: reflexão, rotação e translação para que os alunos percebam, que nesse tipo de transformação, o tamanho se mantém, ou seja, os retângulos são congruentes e esse é também um tipo de semelhança.
Propósito: Fazer com que os alunos percebam que as semirretas nos retângulos semelhantes se interceptam no mesmo ponto. Chame esse ponto de P e conjecture com os alunos. PA = 2PA’ e o mesmo ocorre nos outros vértices. O fator 2 é que vai determinar a razão de semelhança.
Discuta com a turma:
- O que acontece com as medidas dos segmentos PA e PA’? O mesmo ocorre com os segmentos que passam pelos outros vértices?
- Por que será que isso ocorre?
- Como são os lados das figuras que possuem o ponto P? E os ângulos?
- O que acontece se dividirmos a medida de cada lado do retângulo desenhado por vocês pela medida do lado correspondente do retângulo da artista?
- Para retângulos serem semelhantes, é suficiente os ângulos serem congruentes? Justifique.
Discussão da solução
Tempo sugerido: 13 minutos (slides 7, 8, 9, 10 e 11).
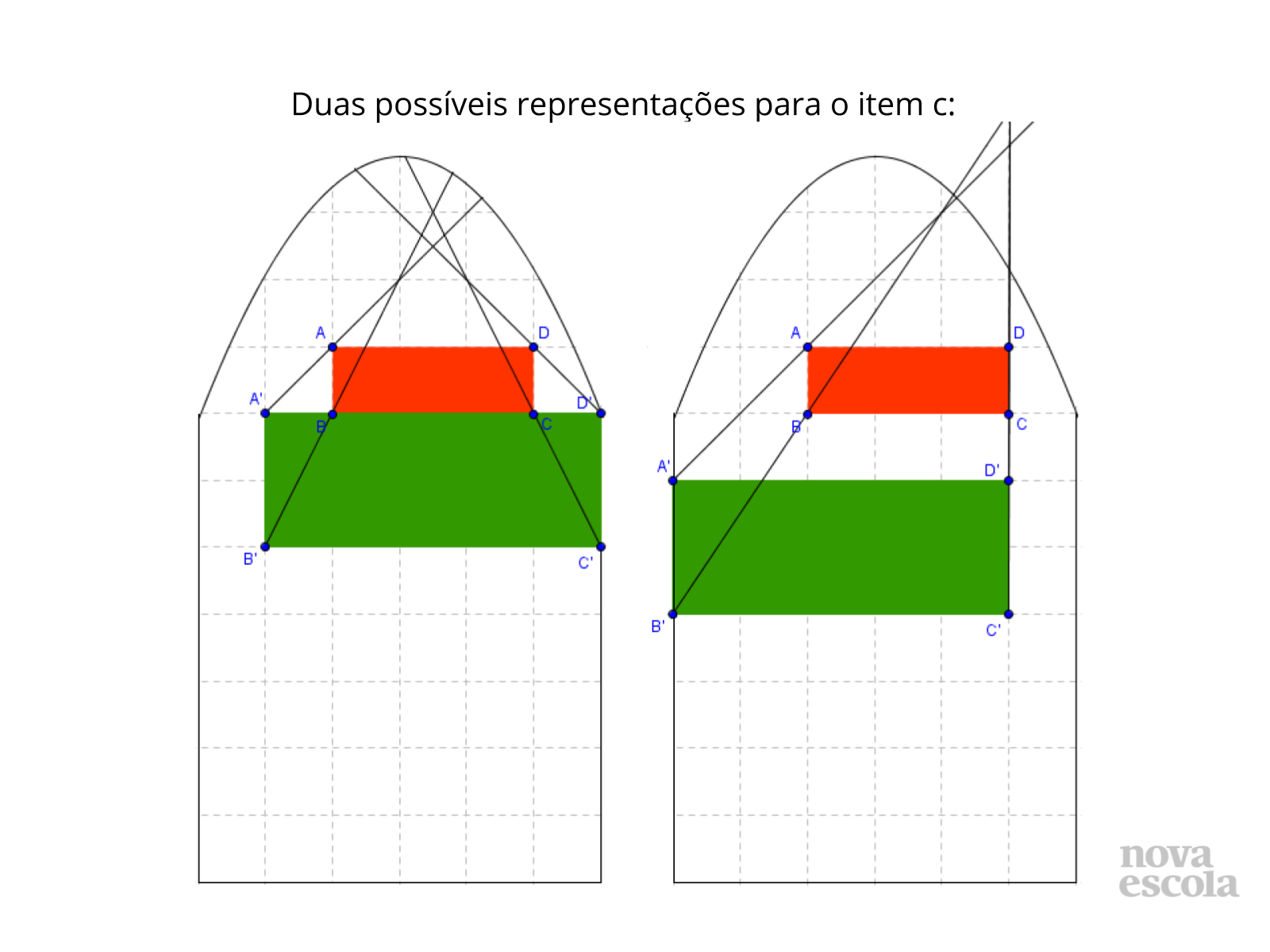
Orientações: Para essa discussão você pode utilizar 2 ou 3 desenhos dos próprios alunos de cada item solicitado. Os alunos, juntamente com você, vão chegando a conclusões a respeito das características de retângulos semelhantes. Vão perceber que a ampliação ou redução de uma figura é semelhante à original quando esta, possui os ângulos correspondentes congruentes e os lados proporcionais. Durante as discussões da solução, aborde figuras nos vitrais que sofreram transformações isométricas: reflexão, rotação e translação para que os alunos percebam, que nesse tipo de transformação, o tamanho se mantém, ou seja, os retângulos são congruentes e esse é também um tipo de semelhança.
Propósito: Fazer com que os alunos percebam que as semirretas nos retângulos semelhantes se interceptam no mesmo ponto. Chame esse ponto de P e conjecture com os alunos. PA = 2PA’ e o mesmo ocorre nos outros vértices. O fator 2 é que vai determinar a razão de semelhança.
Discuta com a turma:
- Por que no retângulo 2 x 5 as semirretas não se interceptam no mesmo ponto? Qual a diferença em relação aos outros dois?
- Como são os lados das figuras que não possuem o ponto P? E os ângulos?
- O que acontece se dividirmos a medida de cada lado do retângulo desenhado por vocês pela medida do lado correspondente do retângulo da artista?
- Para retângulos serem semelhantes, é suficiente os ângulos serem congruentes? Justifique.
Discussão da solução
Tempo sugerido: 13 minutos (slides 7, 8, 9, 10 e 11).
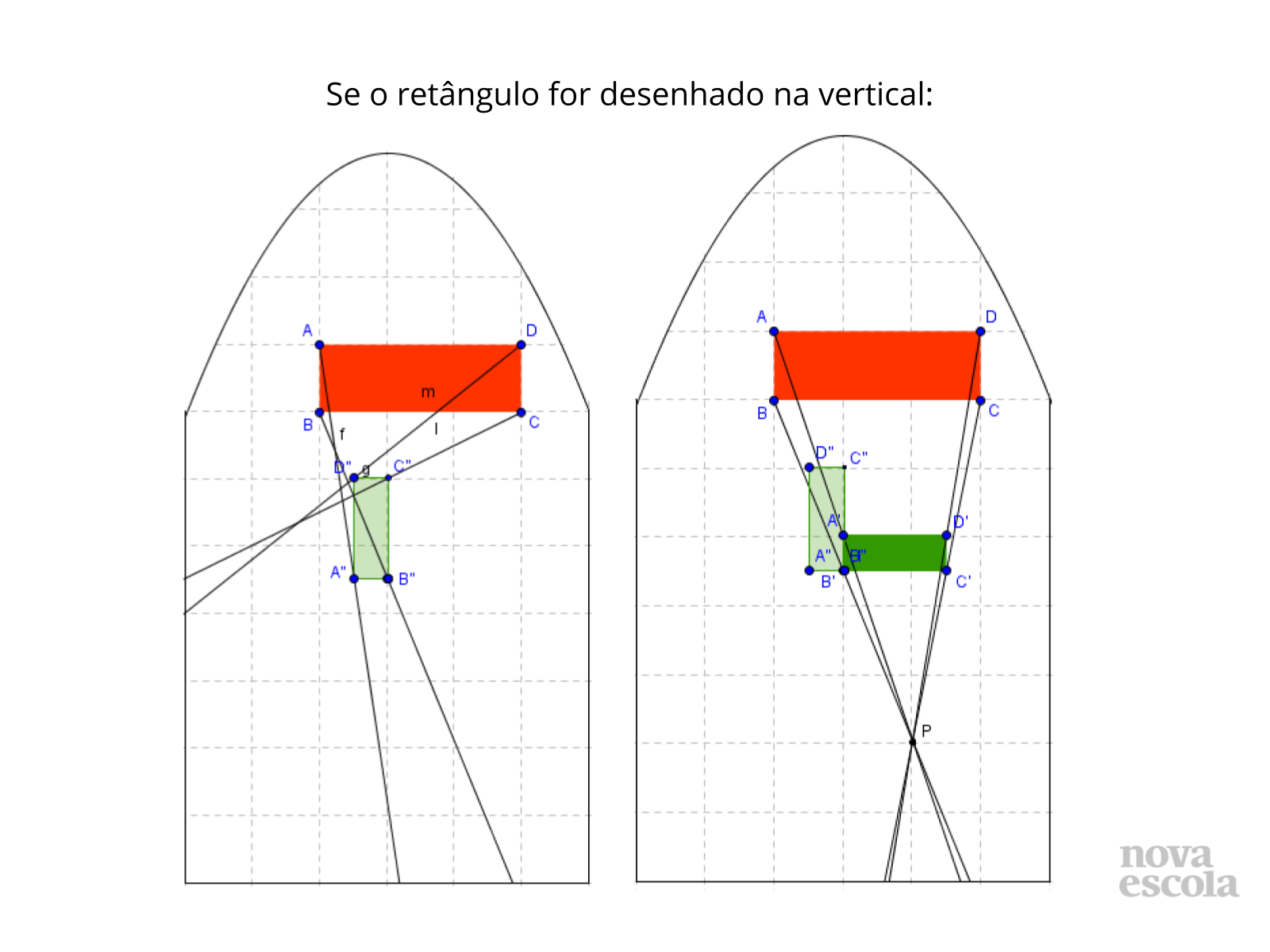
Orientações: Se algum aluno representar um retângulo na vertical ou mesmo se isso não acontecer, aborde outras transformações geométricas. Neste exemplo, a rotação. Após os alunos compreenderem o conceito de semelhança, discuta esta representação com a turma. Mostre a eles que, ao realizar uma rotação da figura, as retas passam a interceptarem-se no mesmo ponto, ou seja, são semelhantes, pois uma é redução da outra.
Propósito: Levar os alunos a compreenderem que o retângulo na vertical é também semelhante ao retângulo laranja, mas ele sofreu outra transformação geométrica após a redução, que é a rotação, e por isso as semirretas não se interceptaram no mesmo ponto. Da mesma forma, os retângulos verdes também são semelhantes, pois são congruentes (semelhança com razão igual a 1).
Discuta com a turma:
- A figura original e a rotacionada têm o mesmo tamanho?
- Existe alguma diferença entre essas figuras?
- O retângulo verde claro é semelhante ao retângulo verde escuro?
- O retângulo verde claro é semelhante ao retângulo laranja?
Discussão da solução
Tempo sugerido: 13 minutos (slides 7, 8, 9, 10 e 11).
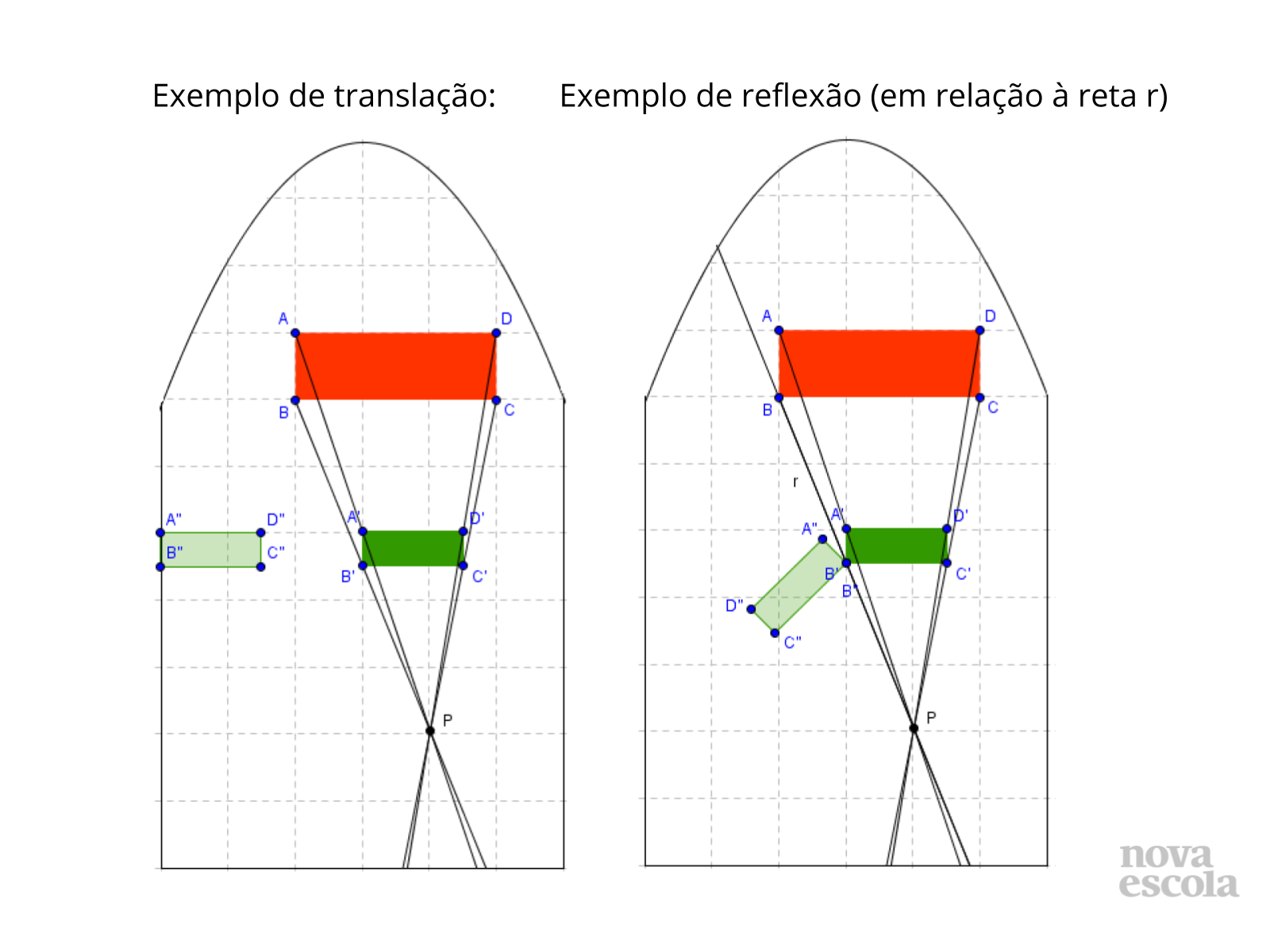
Orientações: Mostre que o mesmo ocorre com qualquer outra transformação geométrica. Utilize as figuras do slide para abordar a translação e a reflexão.
Propósito: Levar os alunos a compreenderem que realizada qualquer transformação geométrica que não altera o tamanho da figura (rotação, translação e reflexão) obtém-se uma figura congruente e, consequentemente, semelhante com razão de semelhança 1.
Sistematização do conceito

Tempo sugerido: 6 minutos (slides 12 e 13).
Orientações: formalize os conceitos que foram aprendidos nesta aula. Você pode, a cada conceito, sempre relembrar utilizando uma construção de aluno ou desenhando novos retângulos no quadro. Por exemplo, quando falar em razão de semelhança, pode-se tomar as medidas de um desenho e realizar os quocientes para mostrar que, em figuras semelhantes, a razão é sempre a mesma.
Propósito: Apresentar os conceitos relacionados à atividade principal.
Sistematização do conceito
Tempo sugerido: 6 minutos (slides 12 e 13).
Orientações: formalize os conceitos que foram aprendidos nesta aula. Você pode, a cada conceito, sempre relembrar utilizando uma construção de aluno ou desenhando novos retângulos no quadro. Por exemplo, quando falar em razão de semelhança, pode-se tomar as medidas de um desenho e realizar os quocientes para mostrar que, em figuras semelhantes, a razão é sempre a mesma.
Propósito: Apresentar os conceitos relacionados à atividade principal.
Encerramento
Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade retomando com os estudantes o que foi revisado e/ou aprendido nesta aula.
Propósito: Apresentar o que foi revisado e aprendido.
Raio X
Tempo sugerido: 7 minutos.
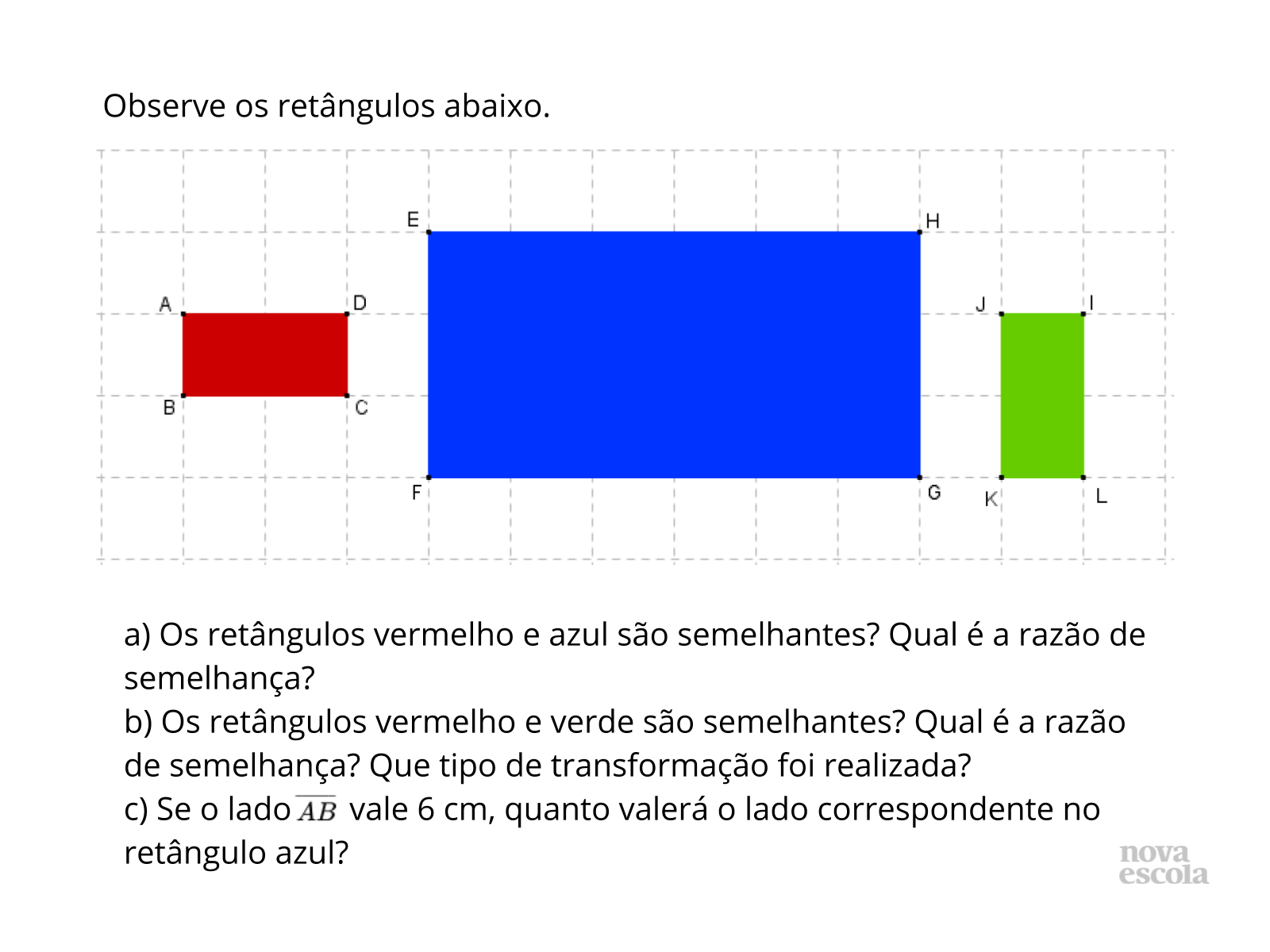
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa. O mais importante é conseguir justificar a semelhança matematicamente e reconhecer o tipo de transformação geométrica utilizada.
Propósito: Auxiliar os alunos a perceberem que somente o formato parecido da figura não é suficiente para verificar a semelhança. Discuta com a turma:
- O que se pode afirmar sobre os ângulos desses retângulos?
- E se o lado EH medir 12 cm, quanto valerá o lado correspondente no retângulo vermelho?
- Se o retângulo azul for rotacionado com qualquer que seja o ângulo de rotação, ele deixa de ser semelhante aos outros dois retângulos? Por quê?
Materiais complementares:
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_12GEO01)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) e papel para anotações.
- Optativas: Calculadora.
Aquecimento
- Pela rede social escolhida, inicie esse contato questionando se seus alunos e alunas lembram das condições de congruência e semelhança de figuras planas. Deixe que deem suas respostas sem correção neste momento.
Atividade principal
- Determine que, acessem o Geogebra (instalado no PC ou online pelo link https://www.geogebra.org/classic?lang=pt_PT)
- Agora solicite que sigam os passos abaixo:
1. Construa um retângulo qualquer aproveitando a malha quadriculada. Utilize a opção: polígono.
2. Construa um outro retângulo qualquer, aproveitando a malha quadriculada, mas sem estar nas mesmas linhas do anterior e de tamanho diferente. Utilize a opção: polígono.
3. Usando a opção RETA, construa retas que liguem os vértices correspondentes, verifique se se cruzam em um único ponto ou não, e anotem as medidas dos lados dos retângulos.
4. Apague os retângulos fazendo Ctrl+z, ou recarregando a página online, ou abrindo um novo arquivo para quem tem o Geogebra instalado, e construa um retângulo com medidas 2 X 4 quadradinhos usando novamente a opção polígono.
5. Construa um outro retângulo com medidas 1 X 2 quadradinhos, usando novamente a opção polígono.
6. Repita as ações do item 3.
Discussão das soluções
- Na discussão das soluções, questione se a posição dos lados do retângulo iria interferir nos encontros das retas e qual seria a condição para que as retas se encontrassem em um ponto.
Sistematização e encerramento
- Faça uma sistematização destacando que na Geometria Euclidiana, duas figuras geométricas são ditas semelhantes sempre que uma puder ser transformada na outra por meio de uma ampliação, redução ou a partir de um movimento rígido (translação, rotação ou reflexão).
- Faça-os reparar que, nas figuras semelhantes, os ângulos têm a mesma medida e os lados são proporcionais.
- Destaque que a congruência é um caso particular de semelhança.
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e relatem suas explorações sobre os desenhos e links acessados.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Eduardo Post
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
Relacionada a EF09MA12 - Reconhecer as condições necessárias e suficientes para que dois triângulos sejam semelhantes.
Objetivos específicos
- Compreender o que é semelhança de retângulos.
- Identificar/calcular a razão de semelhança.
- Relacionar a semelhança entre retângulos e movimentos de transformações no espaço.
Conceito-chave
Razão de semelhança em retângulos.
Recursos necessários
Lápis de colorir, vitrais impressos (malha quadriculada) e régua.
Vocabulário que será adquirido nesta aula
Semelhança entre retângulos, razão de semelhança, ampliação, redução.