Sugestão de adaptação para ensino remoto
Código do plano
MAT4_21GRM_03
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: (apenas se forem absolutamente indispensáveis; caso contrário, inserir todos como opcionais)
- Opcionais: Google Meet, Google Apresentações, Google Formulários, WhatsApp, Mentimeter, Google Documentos.
Para este plano, foque na etapa Atividade Principal.
Aquecimento
O professor pode iniciar o trabalho com questões problematizadoras e que levem os alunos a refletirem sobre situações cotidianas que envolvam o cálculo de perímetro (a necessidade de medir o contorno da quadra da escola para decorá-la, ou ainda o contorno de uma sala para colocar rodapé em toda a sua volta, por exemplo). Esse bate papo pode ser feito de maneira síncrona usando o Google Meet ou via Mentimeter no caso de ser assíncrono, com a socialização das respostas dos alunos para toda a turma posteriormente.
Caso os alunos não tenham acesso aos recursos digitais, o professor pode fazer essa provocação dando exemplos de tais situações no material impresso que acompanhará a próxima etapa (Atividade Principal).
Atividade principal
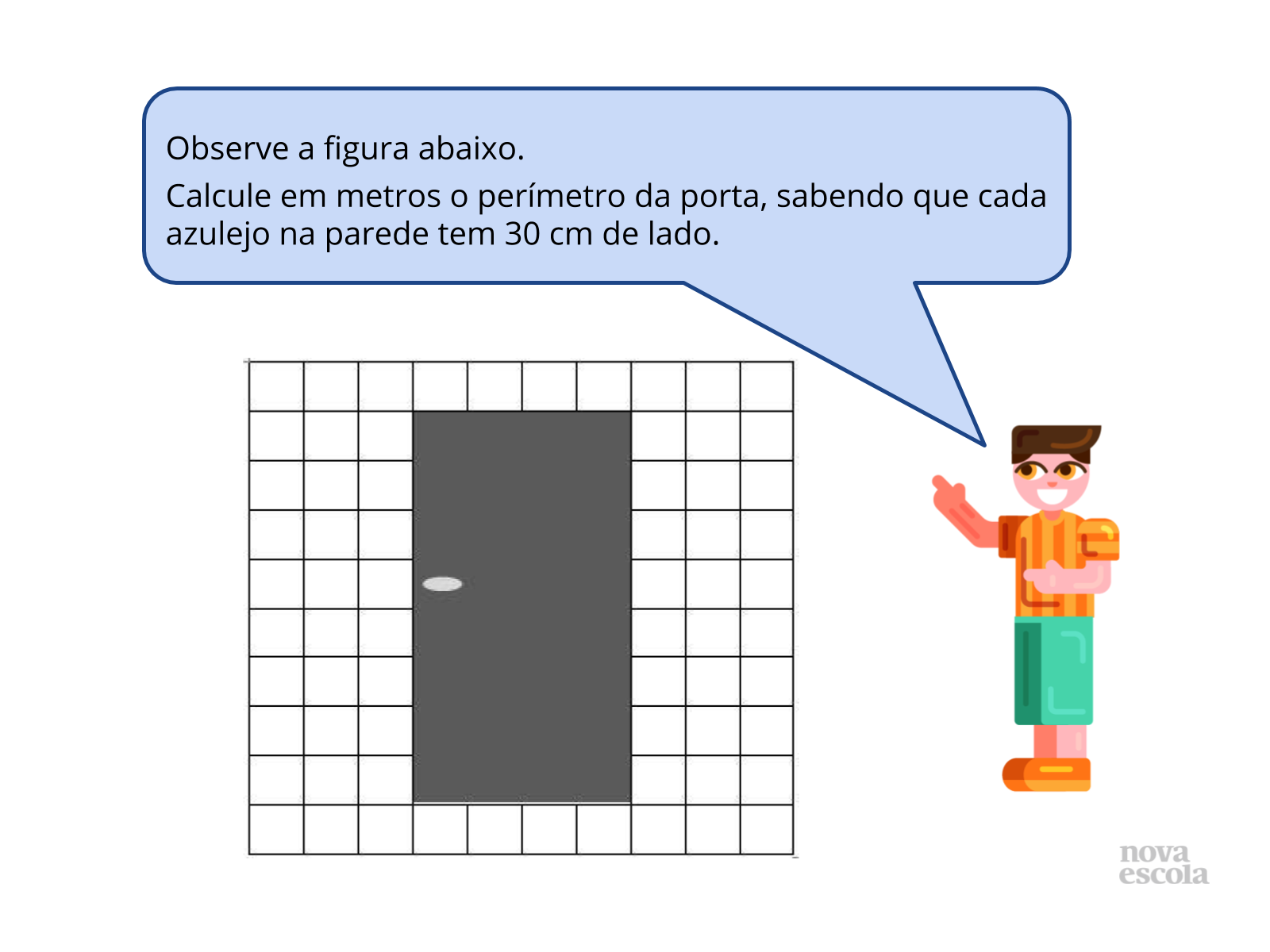
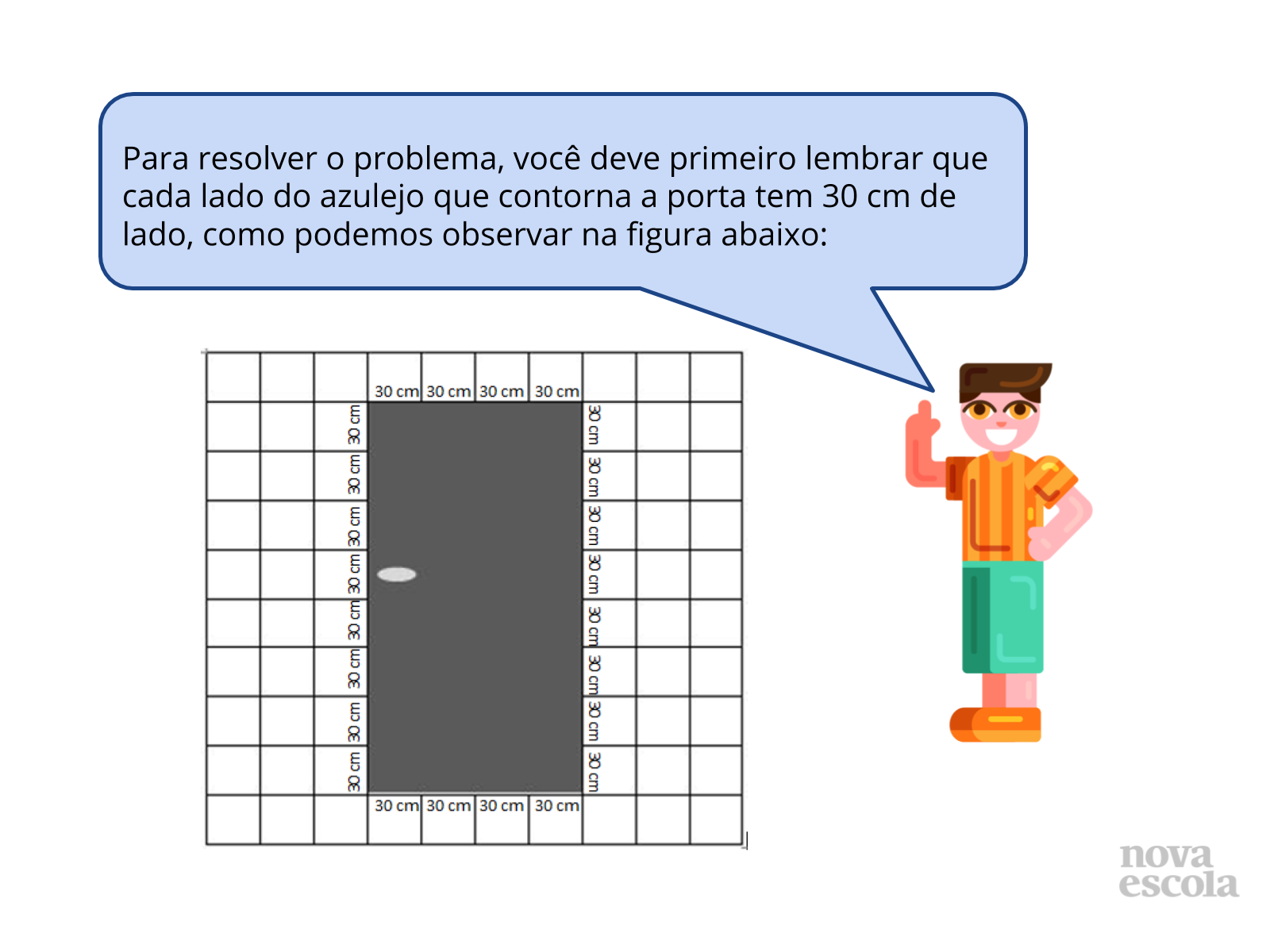
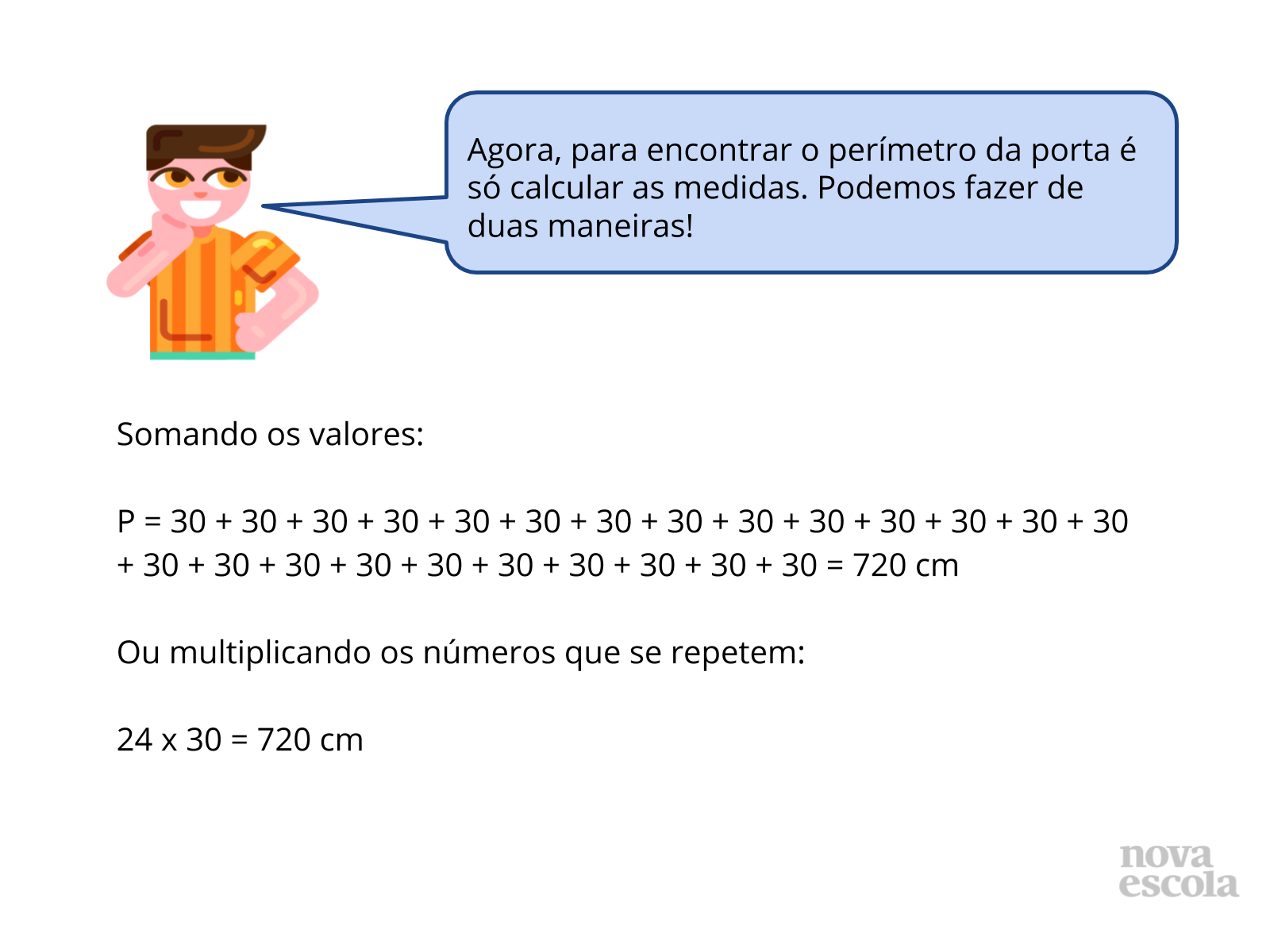
Antes de partir para a atividade propriamente dita, tente encontrar uma situação real similar, com uma porta que possa ter medido o seu contorno e que esteja em uma parede com azulejos idênticos e quadrados (é possível até pesquisar entre os alunos para ver quem teria uma porta assim para fotografar e enviar ao professor via WhatsApp, para que a problematização possa ser construída com um modelo real após o exemplo hipotético levantado aqui no slide da atividade, tornando mais significativo para a turma). As problematizações podem ser organizadas pelo professor usando o Google Apresentações e as dimensões indicadas pelo proprietário da foto recebida. Pedir que os alunos usem o Google Documentos para inserir suas resoluções, explicando como fizeram para chegar às soluções.
Caso os alunos não tenham acesso à internet, o professor pode trabalhar com a atividade disponível aqui em folha impressa para posteriormente discutir as estratégias utilizadas. Lembrar de incluir as questões presentes nas orientações ao professor.
Discussão das soluções
O professor pode colher as estratégias utilizadas e socializa-las, para que os alunos identifiquem resoluções diferentes das escolhidas por eles e, quem sabe, utilizá-las em outras oportunidades de trabalho com perímetro. Isso pode acontecer via Google Apresentações ou em material impresso.
Sistematização
O professor pode fazer uma síntese do que foi trabalhado na aula, usando de exemplos, para que os alunos consultem posteriormente ao estudarem novamente o tema. Isso pode ser feito com o Google Apresentações ou compondo as atividades impressas enviadas, atendendo já a etapa seguinte (Encerramento).
Encerramento
Ver etapa anterior.
Raio X
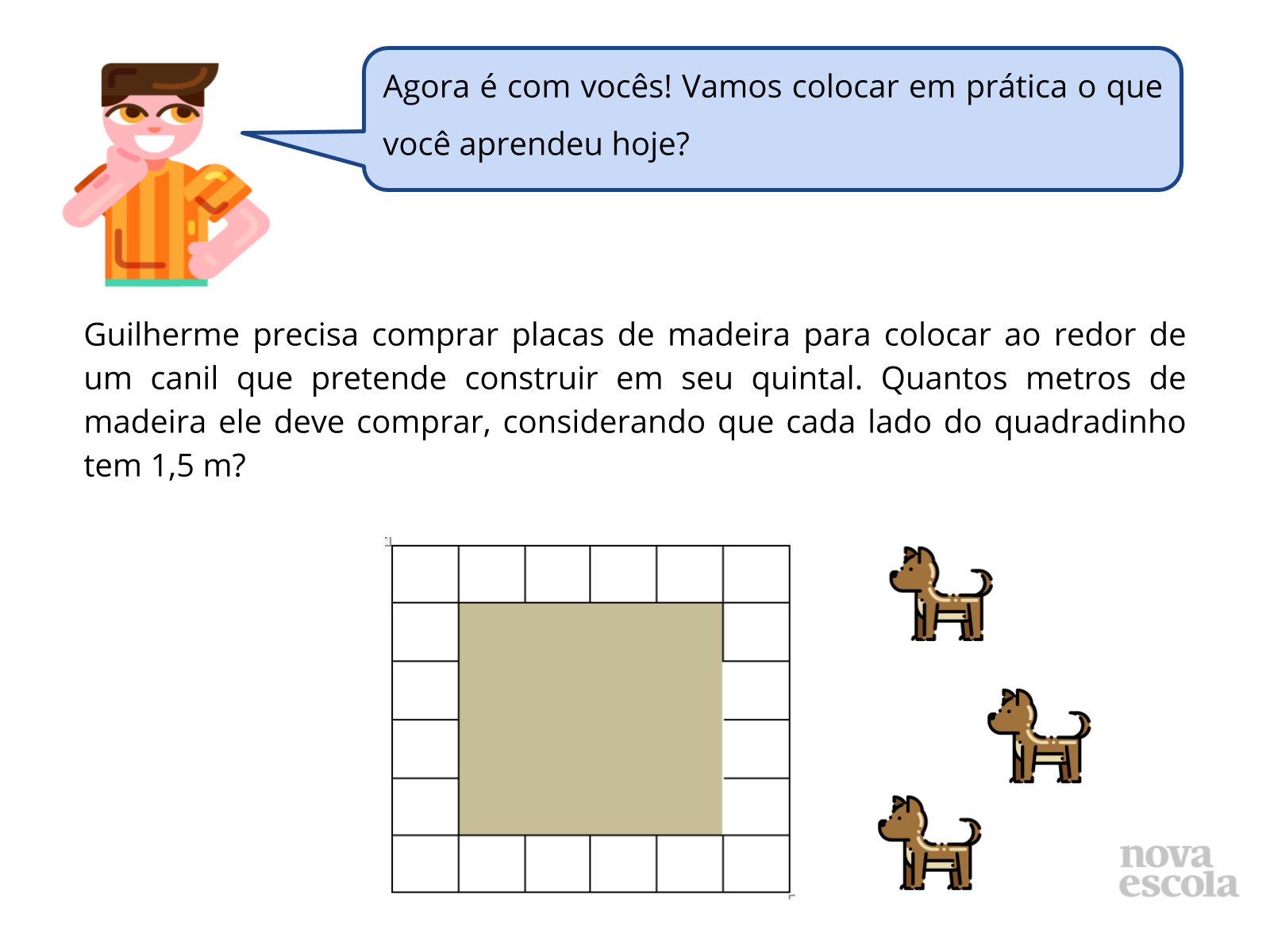
Propor a resolução da atividade do slide e as atividades complementares disponibilizadas. O professor pode inseri-las em arquivo via Google Formulários para facilitar a disponibilização das mesmas. Caso a turma não tenha acesso à internet, o professor pode recorrer aos arquivos já disponíveis aqui no plano de aula de forma impressa.
Convite às famílias
Convidar as famílias a organizar as questões propostas na etapa de Raio X para compor a problemoteca pessoal dos alunos, criando uma frequência de estudos mesmo nos dias em que não tenham aula ou momento de estudo de Matemática.
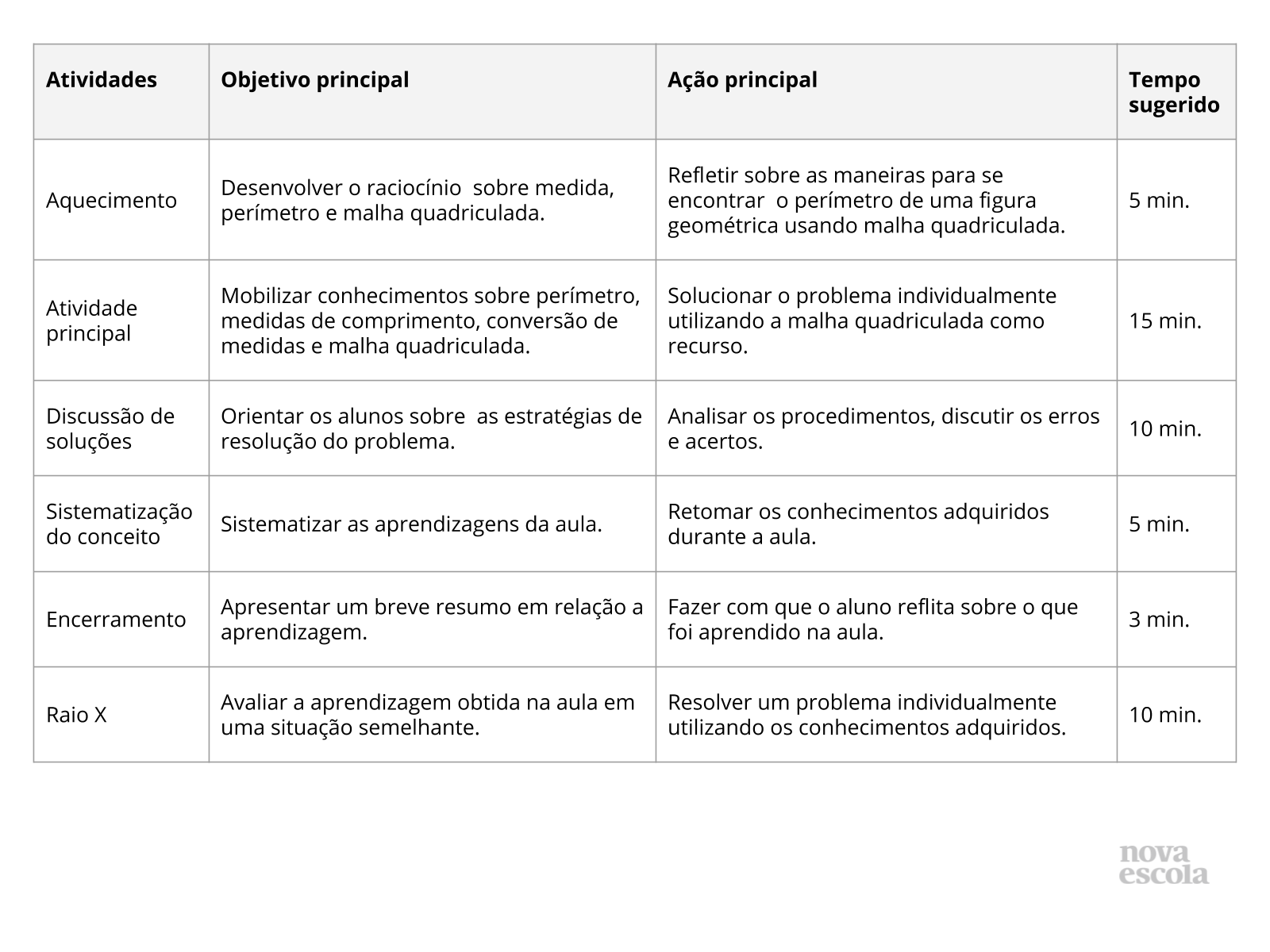 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.