Sugestão de adaptação para ensino remoto
Ferramentas sugeridas
- Essenciais: alguma rede social (Whatsapp, Facebook etc.) e papel para anotações.
- Optativas: calculadora.
Aquecimento
Usando a rede social escolhida, peça para os alunos responderem a duas expressões numéricas sem a ferramenta calculadora neste momento:
a) √64-√36+√144= 8 – 6 + 12 = 14
b) √48-√50+√27= 4√3-5√2+3√3=7√3-5√2
Aqui, sua intenção é relembrar que só podemos somar (ou subtrair) números semelhantes, assim como radicais semelhantes.
Atividade principal
Para esta atividade, também será preciso usar o conhecimento sobre o cálculo de área de um quadrado. Vale fazer uma lembrança que A= l², onde A é a área e l o lado do quadrado.
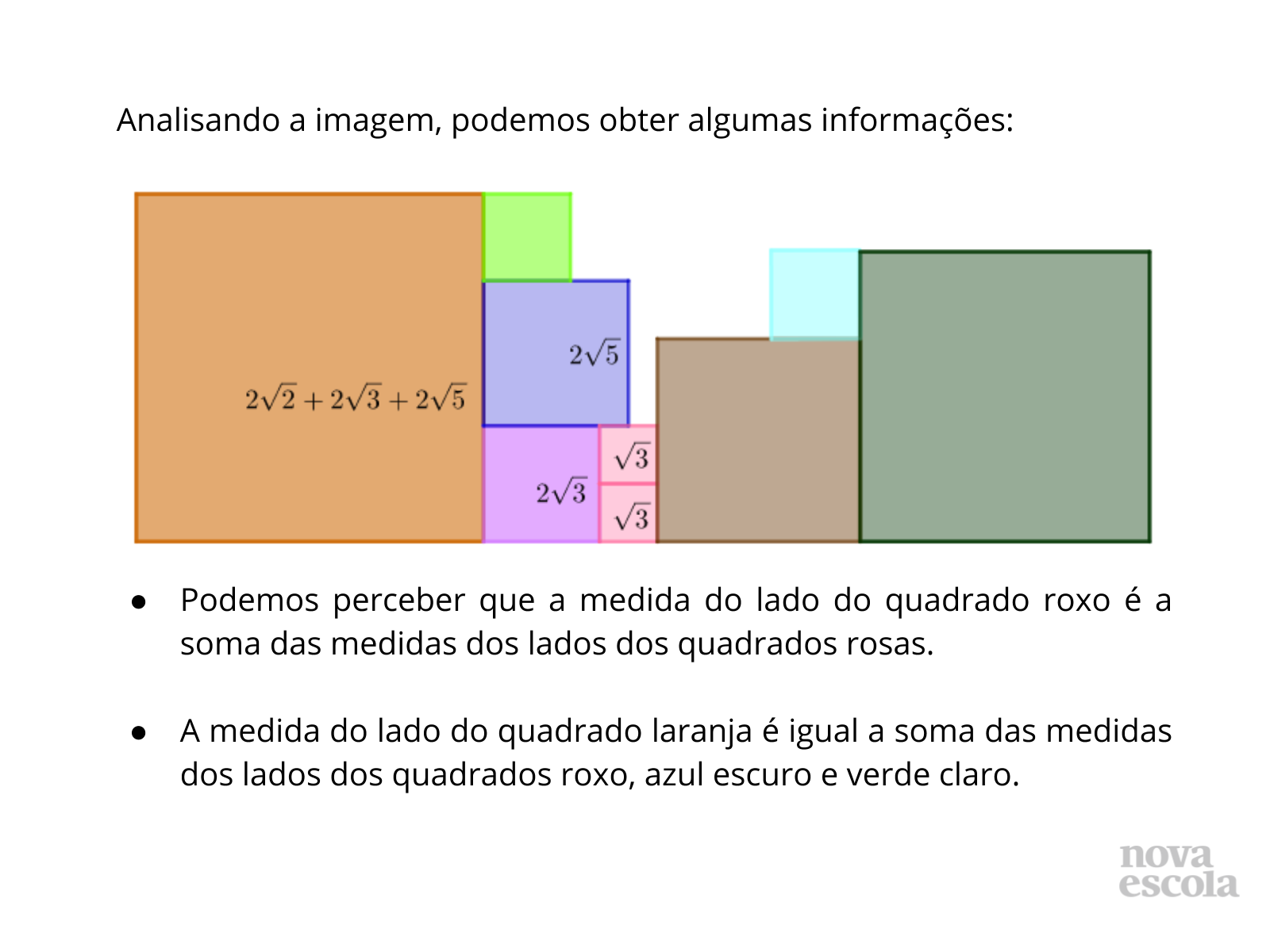
Peça para fazerem um esboço de 5 quadrados de tamanhos (áreas) diferentes, mas que estejam “encostados” uns nos outros formando uma fila, considerando e estimando que:
- O primeiro tem área de 20cm²;
- O segundo tem área de 8cm²;
- O terceiro tem área de 3cm²;
- O quarto tem área de 12cm²;
- O quinto tem os lados medindo a soma dos lados dos outros quatro quadrados.
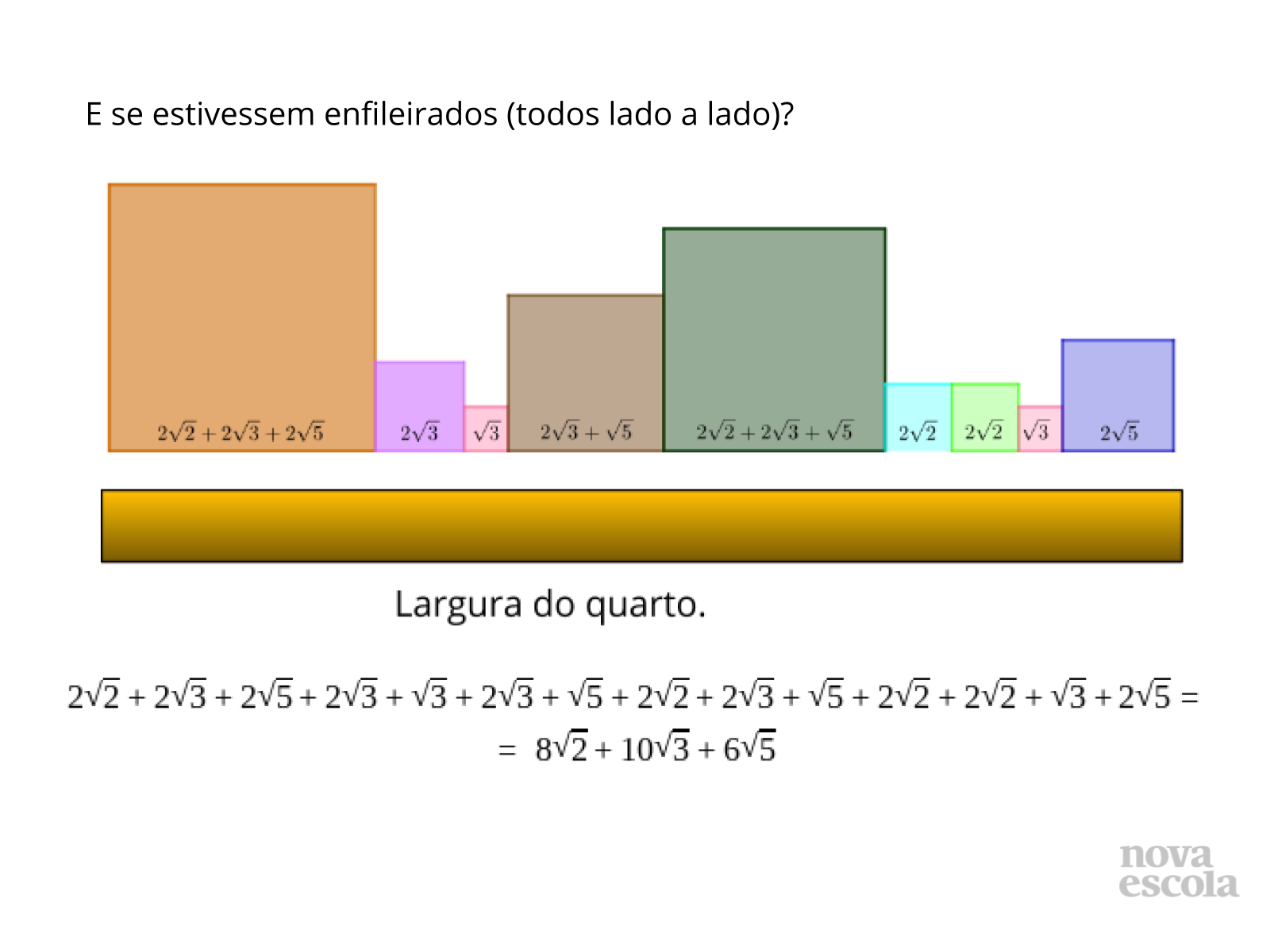
A proposta é descobrir qual é o comprimento ocupado pela junção destes 5 quadrados.
Painel de soluções
1) A=20, logo, l=√20, que, ao fatorar, temos, 2√5.
2) A=8, logo, l=√8, que, ao fatorar, temos, 2√2.
3) A=3, logo, l=√3,
4) A=12, logo, l=1√2, que, ao fatorar, temos, 2√3
5) l=2√5+2√2+√3+2√3= 2√5+2√2+3√3, pois somamos os radicais semelhantes.
Assim, o comprimento=2√5+2√2+3√3+2√5+2√2+3√3=4√5+2√2+6√3 cm
Sistematização e encerramento
Ressalte que usamos as raízes quadradas para encontrar lados de quadrados e que é recomendável:
- Realizar a fatoração para saber se aparecem radicais semelhantes com outras medidas;
- Lembrar que só podem ser somados (ou subtraídos) esses irracionais representados por raízes se tiverem o mesmo radical.
Ressalte também a importância de se notar quando é preciso somar ou subtrair radicais, como a junção de comprimentos irracionais.
Raio X
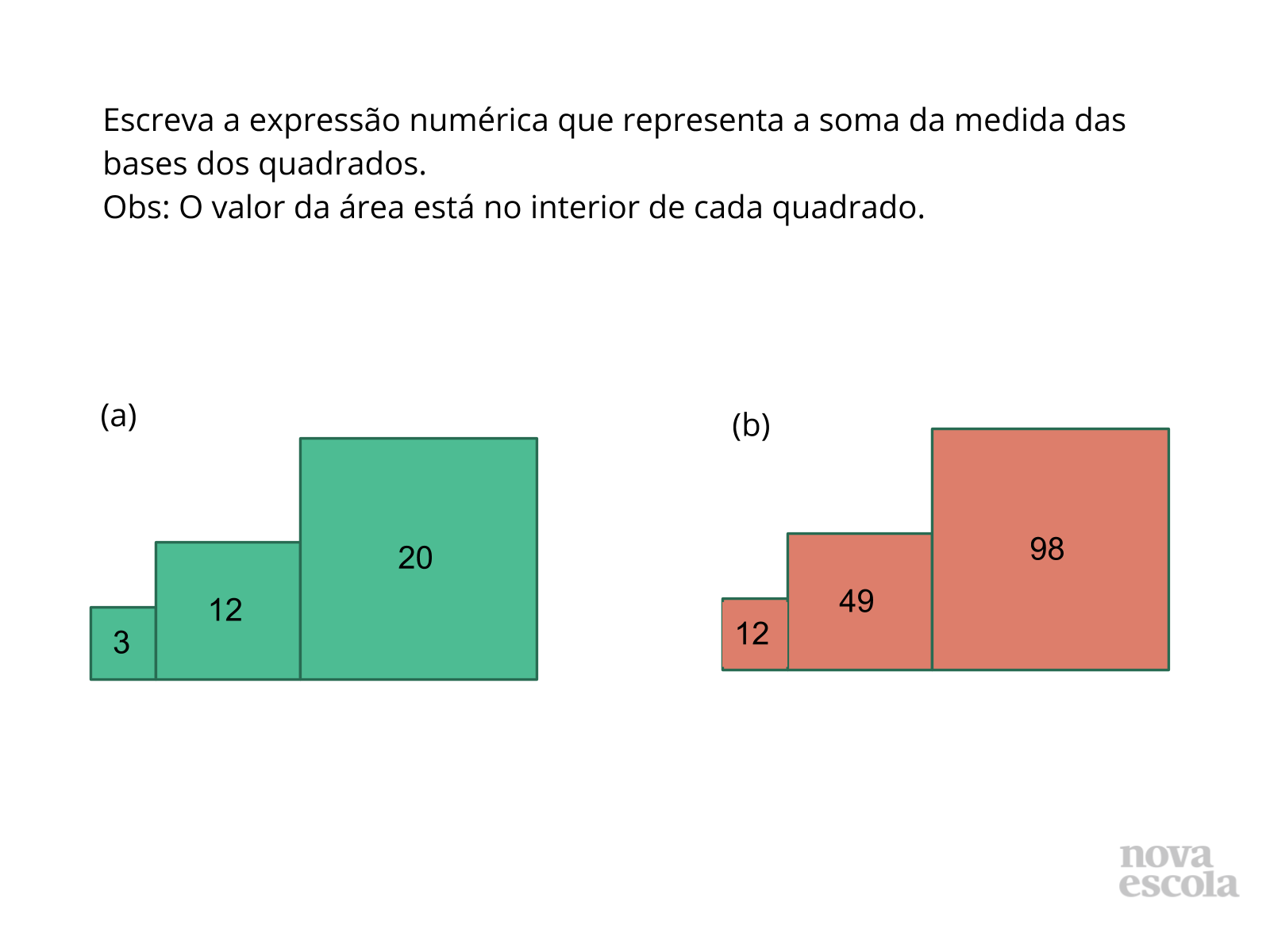
Peça para que seus alunos apresentem a expressão numérica relativa à soma dos lados dos quadrados com área: 3cm², 12cm² e 20cm².
Convite às famílias
Peça para seus alunos verificarem com os familiares, próximos neste momento, se conseguem produzir quadrados perfeitos e de tamanhos diferentes de modo que os lados cubram todo o comprimento da folha, a partir de uma folha de tamanho A4. Lembre-os que essa é apenas uma atividade recreativa.
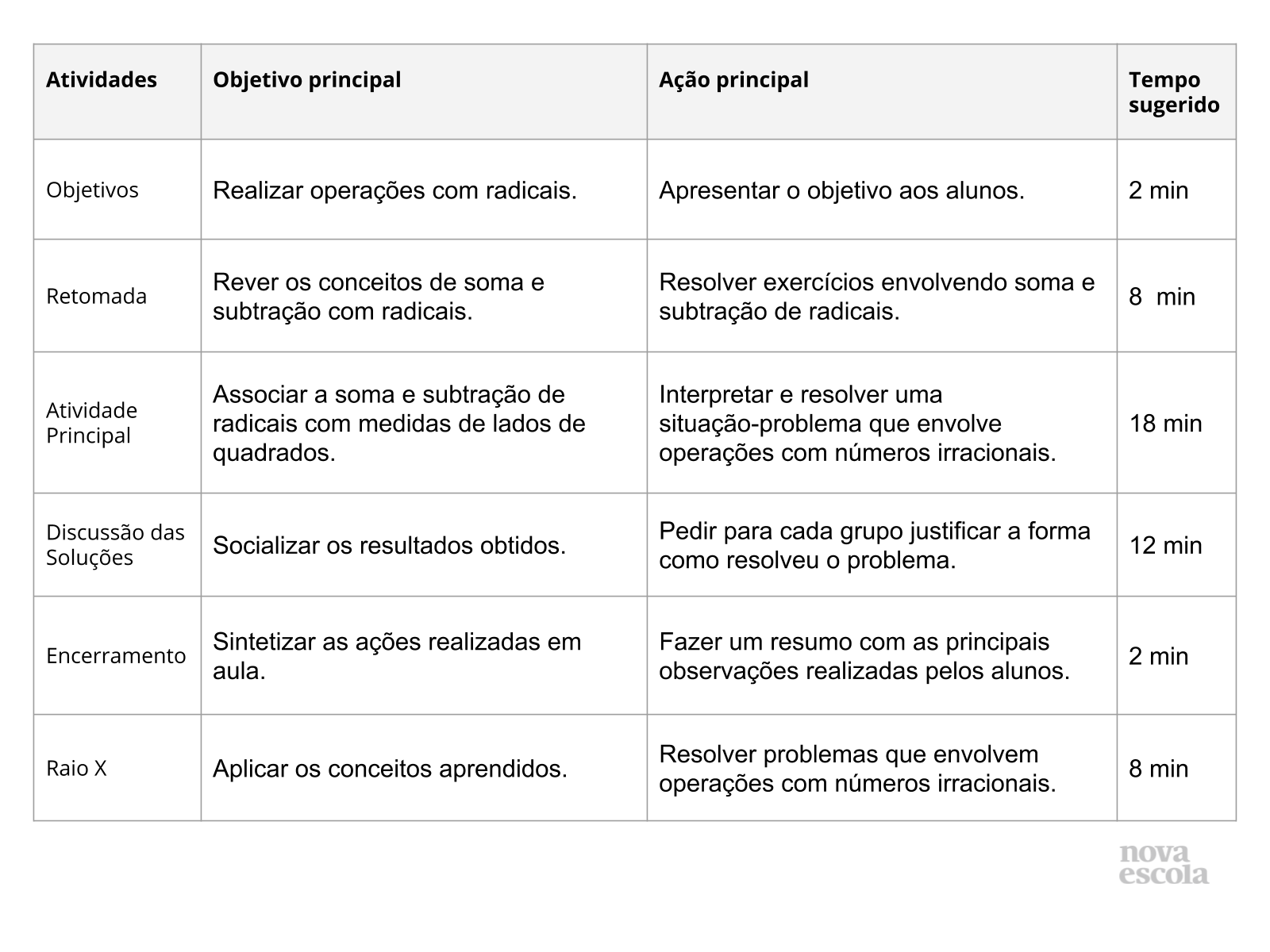 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.