Atividade Principal
Plano de Aula
Plano de aula: Divisão de racionais fracionários
Plano 3 de uma sequência de 10 planos. Veja todos os planos sobre Operações com racionais
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Rosiane F. Prates
Mentora: Débora Vieira de Moraes
Revisor: Rodrigo Morozetti Blanco
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA08 - Conceituar, relacionar aplicação dos números racionais dentro da divisão, desenvolver habilidades estratégicas de cálculo entre os racionais.
Conhecimentos que a turma deve dominar:
Domínio do conceito de fração, identificar a relação entre os conjuntos numéricos (racionais, inteiros e naturais); quatro operações com inteiros, comparação, diferenciação entre inteiro e fração.
Objetivos específicos
- Identificar os racionais fracionários positivos e negativos;
- realizar divisão com racionais fracionários positivos e negativos.
Conceito-chave
Divisão com racionais.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
- Projetor multimídia (caso não se utilize impressões)
Habilidades BNCC:
Objetivos de aprendizagem
- Identificar os racionais fracionários positivos e negativos;
- realizar divisão com racionais fracionários positivos e negativos.
Resumo da aula
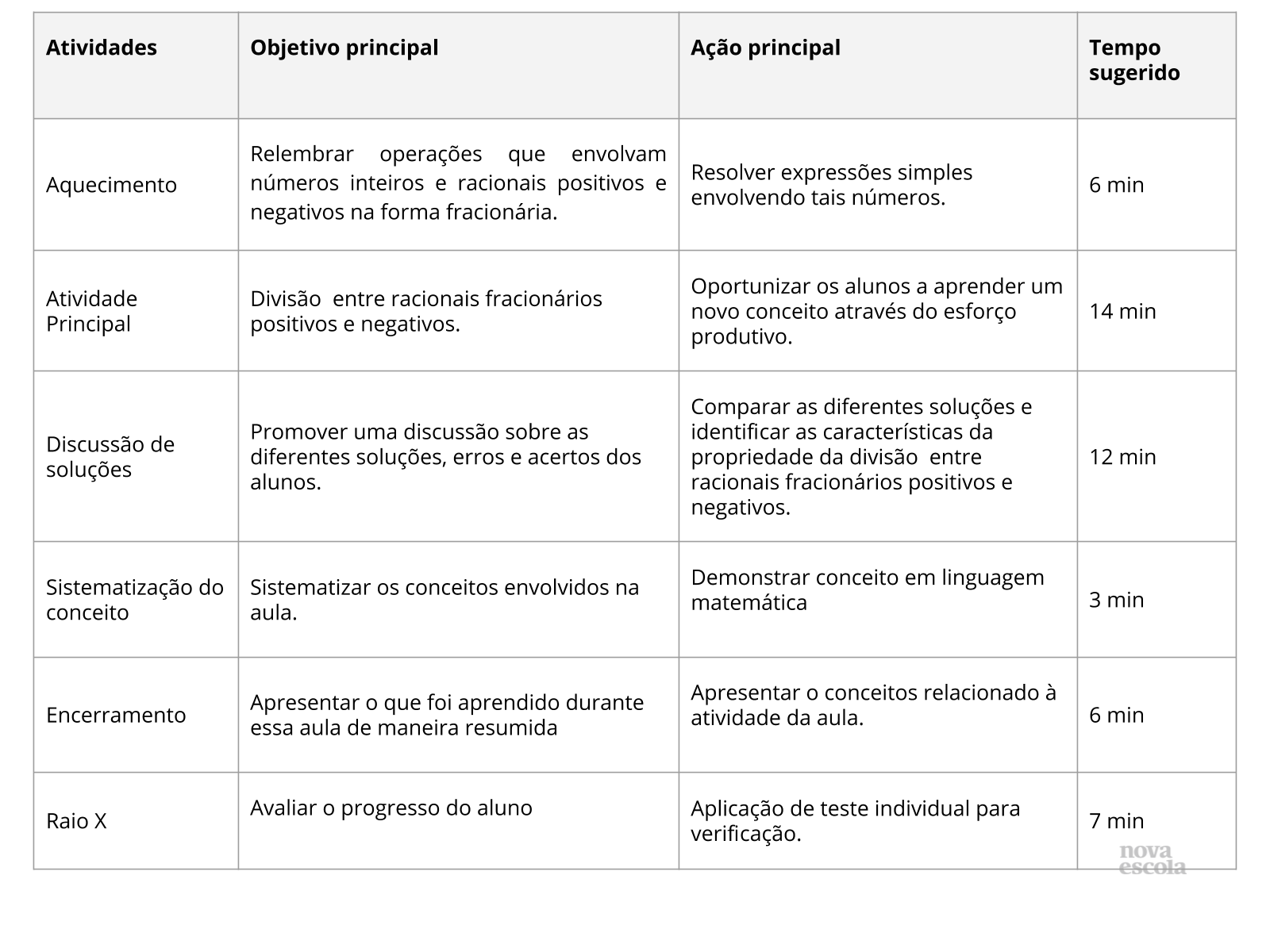
Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 min
Orientações: Apresentar o objetivo da aula de maneira breve, mostrando ao aluno o foco da aula, sem desconsiderar que ele precisará dos conceitos adquiridos anteriormente referente aos números naturais, inteiros e racionais.
Propósito: compartilhar o objetivo da aula
Aquecimento

Tempo sugerido: 6 min
Orientação: Apresente o slide aos alunos ou escreva a atividade na lousa. Deixe que os alunos pensem individualmente sobre as questões antes de conversar com seus colegas. Em seguida faça uma correção oral e coletiva da atividade, perguntando a eles a quais conclusões chegaram.
Espera-se que percebam que as únicas frações equivalentes são -2/4 e -1/2. Com essa atividade eles devem se lembrar que para simplificar frações basta dividir numerador e denominador pelo mesmo número (que deve ser um divisor comum aos dois termos da fração). Devem se lembrar também que ½ e -½ não são equivalentes, mas opostas.
De acordo com as frações escolhidas para fazer as multiplicações, mostre a eles que multiplicar uma fração por ½ ou por -½ gera resultados opostos. Além disso, ao multiplicar uma fração por -½ ou por -2/4 obtém-se também resultados equivalentes.
Espera-se que eles se lembrem que na multiplicação de frações o numerador do produto é o produto dos numeradores e o denominador do produto é o produto dos denominadores.
Propósito: Relembrar conceitos já aprendidos e que serão necessários à aula.
Discuta com a turma:
- Como podemos verificar se duas frações são equivalentes?
Atividade principal

Tempo sugerido: 14 min
Orientação: Essa atividade está dividida em duas partes (slides 4 e 5). O ideal é que eles façam primeiro a atividade do slide 4 para depois abordar a atividade do slide 5, mas caso a sala tenha ritmos muito distintos é possível imprimir as atividades e entregar as duas para os alunos deixando que pensem nelas simultaneamente. As atividades também podem ser realizadas individualmente ou em duplas. A proposta é que eles utilizem o que sabem sobre multiplicação de frações para deduzir o fator que está faltando. Com base nessa resposta, percebam que a divisão de frações é idêntica à multiplicação pela fração inversa.
É possível que eles tragam esse conhecimento de anos anteriores. Nesse momento é essencial que eles formalizem esse algoritmo incluindo o uso do sinal no caso das operações envolvendo frações negativas.
Propósito: Identificar as expressões, efetuar a divisão, perceber se há ou não relação com a multiplicação, e ainda, verificar a possibilidade de transformá-las em uma fração irredutível.
Discuta com a turma:
- Quando dividimos frações podemos dividir os numeradores e os denominadores separadamente?
- Essa prática funciona todas as vezes, independente dos números das frações?
- As regras de sinal usadas na divisão de números inteiros é válida para a divisão de números racionais?
Materiais complementares:
Atividade principal

Tempo sugerido: 14 min
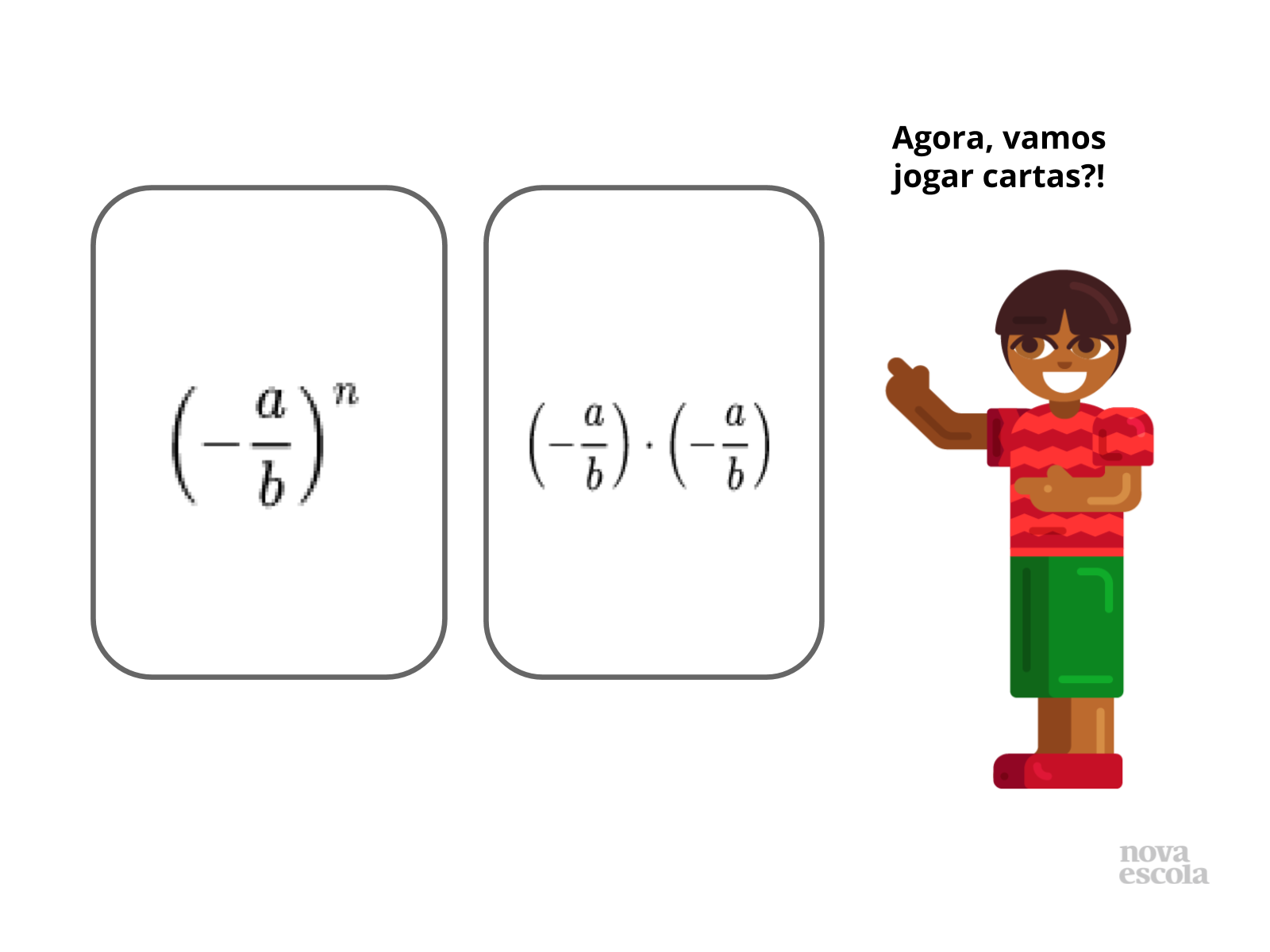
Orientação: aqui será apresentada para a turma a atividade principal, onde os alunos precisarão interpretar as perguntas e responder de acordo com o desafio da atividade que é formar as expressões de acordo com a combinação dos números do 1º quadro com os números do 2º quadro e assim obter nove expressões, obtendo os resultados para posterior análise de acordo com as perguntas. Sugestão: essa atividade pode ser proposta em dupla, com intuito de permitir que os alunos compartilhem os anseios ao tentar resolver atividade e ainda propor que em um primeiro momento eles sentados em dupla, mas individualmente façam a tentativa de resolução a fim de fixar a quantidade máxima de expressões e em um segundo momento verifiquem com sua dupla se foram encontradas as mesmas expressões, na mesma ordem , se os resultados foram iguais ou não, se a ordem interfere ou não no resultado final.
Propósito: Identificar as expressões, efetuar a divisão, perceber se há ou não relação com a multiplicação, e ainda, verificar a possibilidade de transformá-los em uma fração irredutível.
Discuta com a turma:
- O que percebemos nessa atividade?
- Sobre a posição dos números na expressão, podemos afirmar que a alteração interfere no resultado?
Tempo sugerido: 14 min
Orientação: Essa atividade está dividida em duas partes (slides 4 e 5). O ideal é que eles façam primeiro a atividade do slide 4 para depois abordar a atividade do slide 5, mas caso a sala tenha ritmos muito distintos é possível imprimir as atividades e entregar as duas para os alunos deixando que pensem nelas simultaneamente. As atividades também podem ser realizadas individualmente ou em duplas. A proposta é que eles utilizem o que sabem sobre multiplicação de frações para deduzir o fator que está faltando. Com base nessa resposta, percebam que a divisão de frações é idêntica à multiplicação pela fração inversa.
É possível que eles tragam esse conhecimento de anos anteriores. Nesse momento é essencial que eles formalizem esse algoritmo incluindo o uso do sinal no caso das operações envolvendo frações negativas.
Propósito: Identificar as expressões, efetuar a divisão, perceber se há ou não relação com a multiplicação, e ainda, verificar a possibilidade de transformá-las em uma fração irredutível.
Discuta com a turma:
- Quando dividimos frações podemos dividir os numeradores e os denominadores separadamente?
- Essa prática funciona todas as vezes, independente dos números das frações?
- As regras de sinal usadas na divisão de números inteiros é válida para a divisão de números racionais?
Discussão das soluções (slides 6 a 8)
Tempo sugerido: 8 min
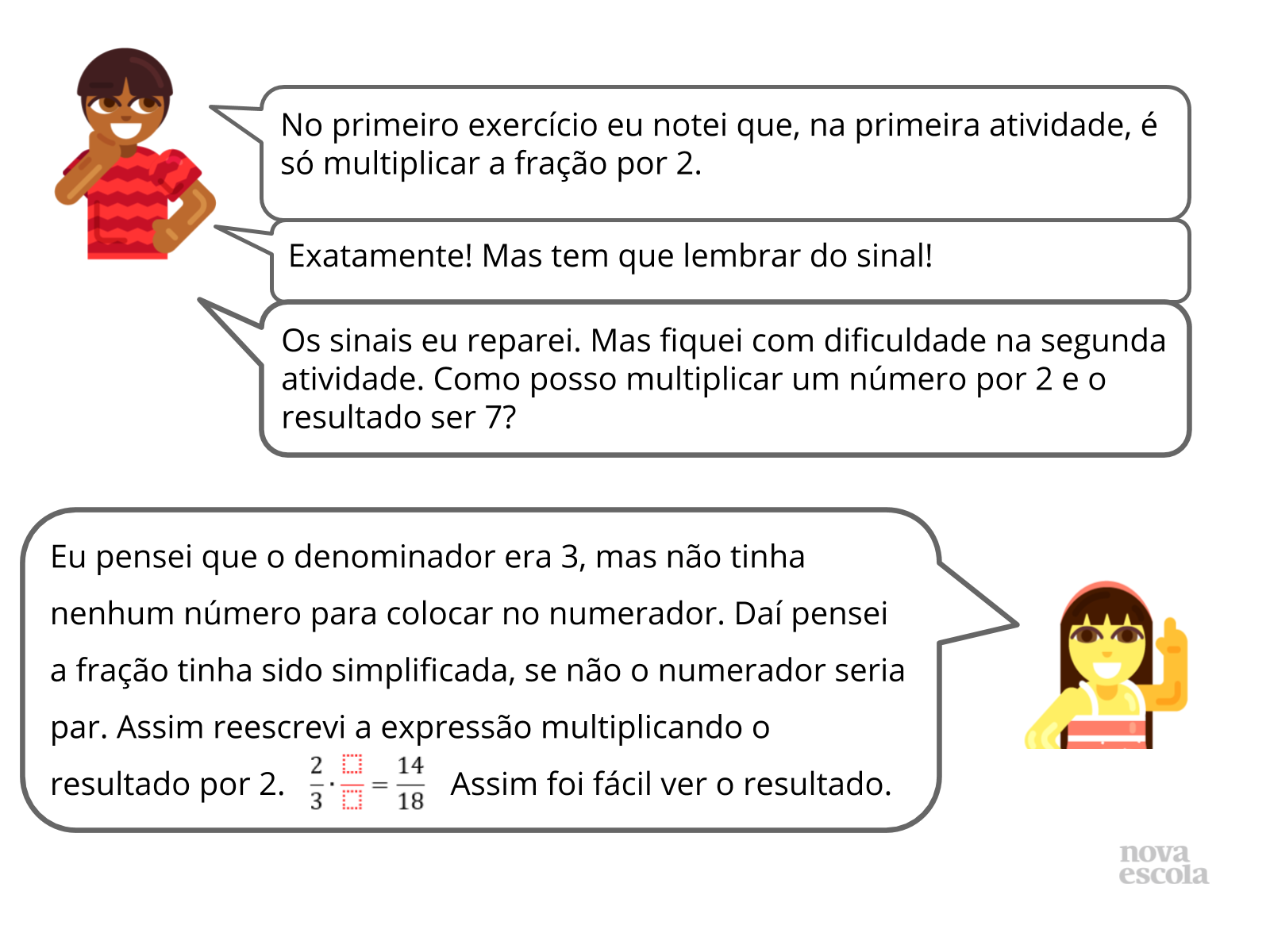
Orientação: Nesse momento é essencial trazer a voz dos alunos para que reflitam sobre suas próprias soluções, os procedimentos escolhidos, seus erros e acertos. A partir do confrontamento de suas estratégias deve ser possível observarem a resposta certa para as operações propostas e alguns caminhos certos para a definição do algoritmo da divisão de frações. Nesse momento é essencial que percebam que as regras de sinal válidas na divisão de inteiros valem também na divisão de racionais. O procedimento da divisão pode ser formalizado num momento posterior, após o debate inicial.
Caso algum aluno apresente uma solução errada, peça que ele explique como chegou àquele resultado. Da mesma forma, caso algum aluno defina uma maneira incorreta de realizar a operação de divisão, peça que ele teste sua definição algumas vezes. Proponha para ele exemplos que darão errado para que ele confronte e refaça sua ideia.
Propósito: orientar os alunos para que apresentem para a turma os procedimentos usados para a resolução da atividade, com vista para possíveis erros e dificuldades, a fim de que todos os alunos consiga compreender o método de resolução.
Discuta com a turma:
- Existe alguma relação entre a multiplicação e a divisão?
Discussão das soluções (slides 6 a 8)
Tempo sugerido: 8 min
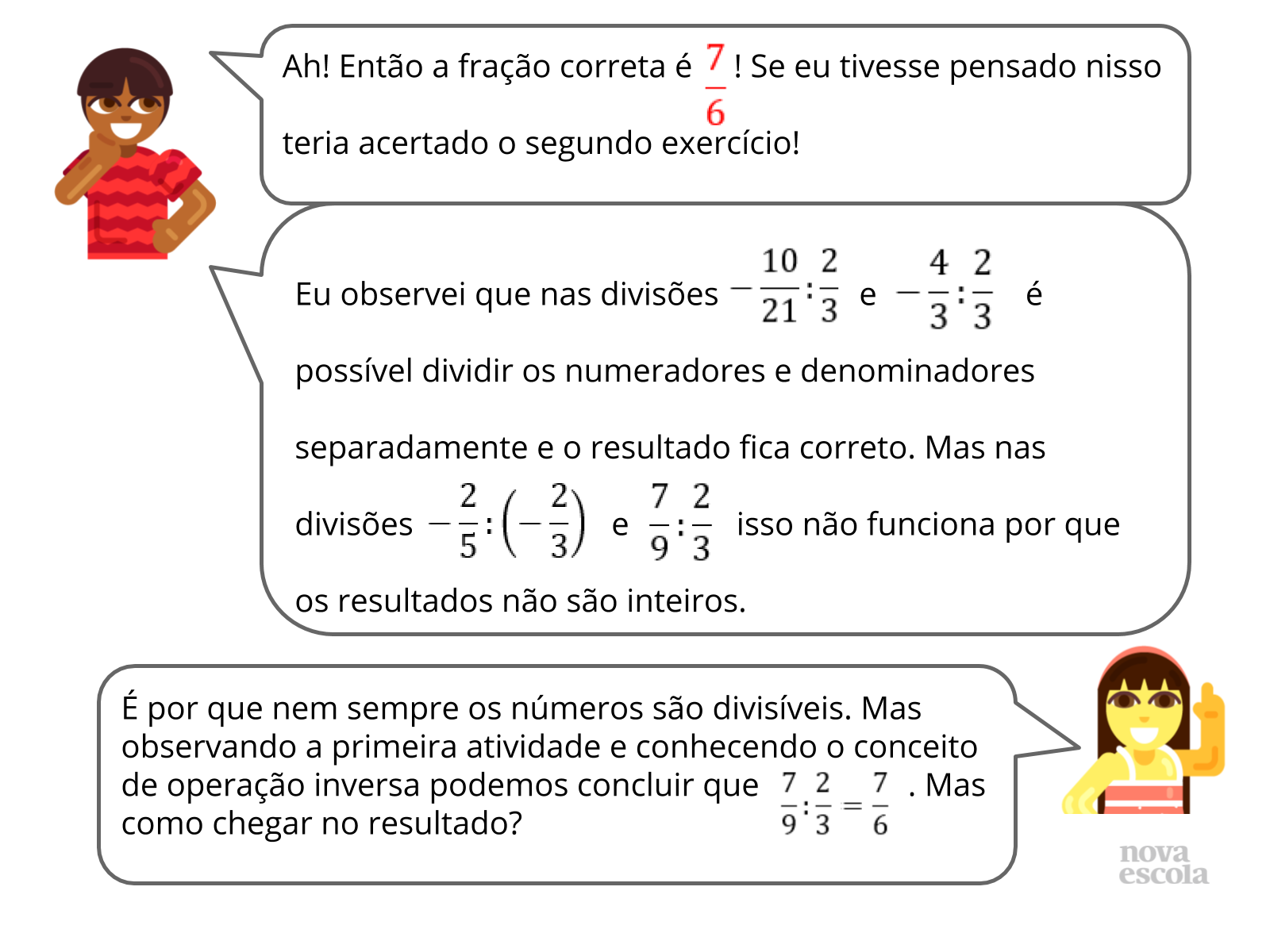
Orientação: Nesse momento é essencial trazer a voz dos alunos para que reflitam sobre suas próprias soluções, os procedimentos escolhidos, seus erros e acertos. A partir do confrontamento de suas estratégias deve ser possível observarem a resposta certa para as operações propostas e alguns caminhos certos para a definição do algoritmo da divisão de frações. Nesse momento é essencial que percebam que as regras de sinal válidas na divisão de inteiros valem também na divisão de racionais. O procedimento da divisão pode ser formalizado num momento posterior, após o debate inicial.
Caso algum aluno apresente uma solução errada, peça que ele explique como chegou àquele resultado. Da mesma forma, caso algum aluno defina uma maneira incorreta de realizar a operação de divisão, peça que ele teste sua definição algumas vezes. Proponha para ele exemplos que darão errado para que ele confronte e refaça sua ideia.
Propósito: orientar os alunos para que apresentem para a turma os procedimentos usados para a resolução da atividade, com vista para possíveis erros e dificuldades, a fim de que todos os alunos consiga compreender o método de resolução.
Discuta com a turma:
- Existe alguma relação entre a multiplicação e a divisão?
Discussão das soluções(slides 6 a 8)
Tempo sugerido: 8 min
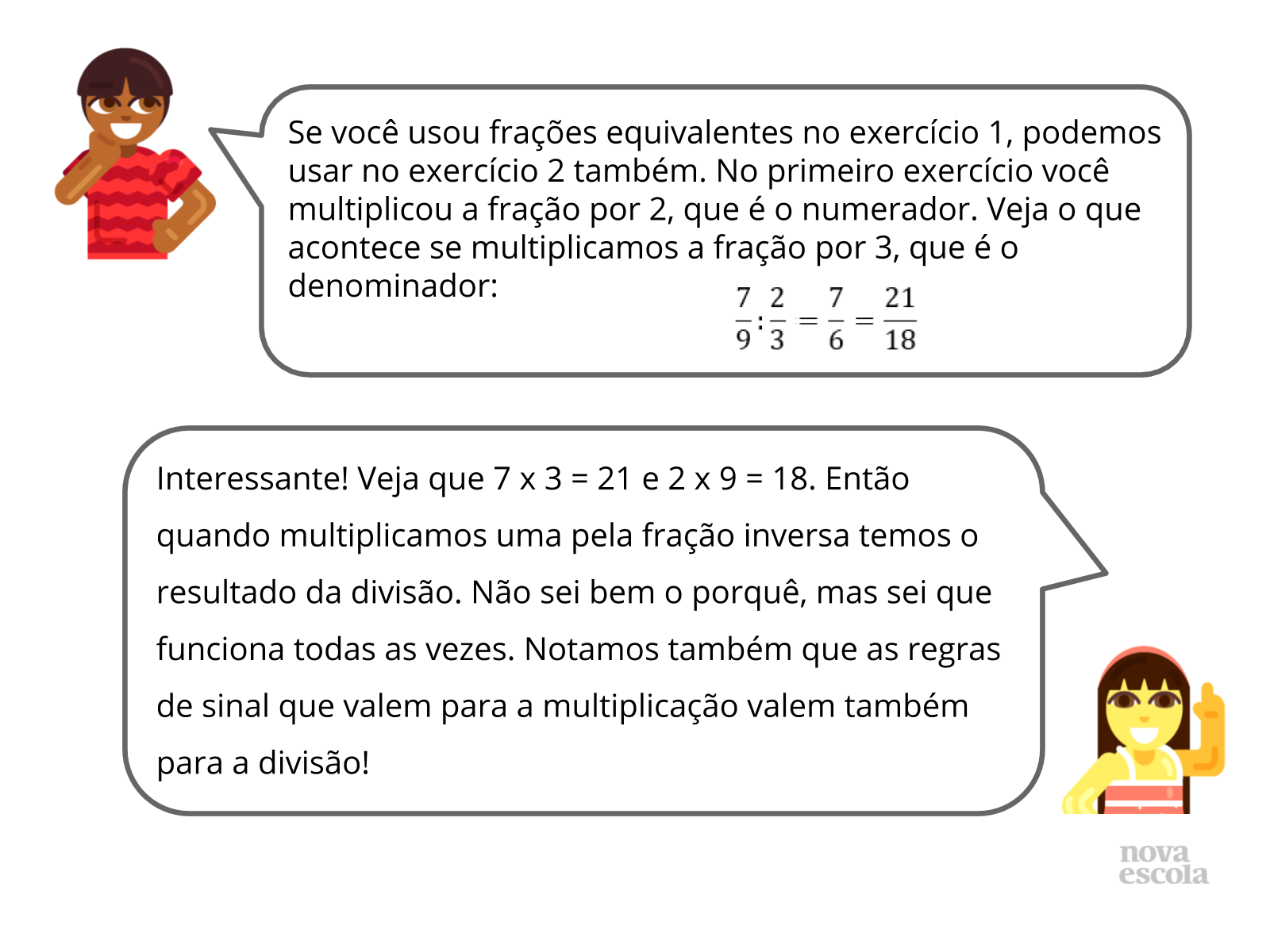
Orientação: Nesse momento é essencial trazer a voz dos alunos para que reflitam sobre suas próprias soluções, os procedimentos escolhidos, seus erros e acertos. A partir do confrontamento de suas estratégias deve ser possível observarem a resposta certa para as operações propostas e alguns caminhos certos para a definição do algoritmo da divisão de frações. Nesse momento é essencial que percebam que as regras de sinal válidas na divisão de inteiros valem também na divisão de racionais. O procedimento da divisão pode ser formalizado num momento posterior, após o debate inicial.
Caso algum aluno apresente uma solução errada, peça que ele explique como chegou àquele resultado. Da mesma forma, caso algum aluno defina uma maneira incorreta de realizar a operação de divisão, peça que ele teste sua definição algumas vezes. Proponha para ele exemplos que darão errado para que ele confronte e refaça sua ideia.
Propósito: orientar os alunos para que apresentem para a turma os procedimentos usados para a resolução da atividade, com vista para possíveis erros e dificuldades, a fim de que todos os alunos consiga compreender o método de resolução.
Discuta com a turma:
- Existe alguma relação entre a multiplicação e a divisão?
Sistematização (slides 9 e 10)

Tempo sugerido: 3 min
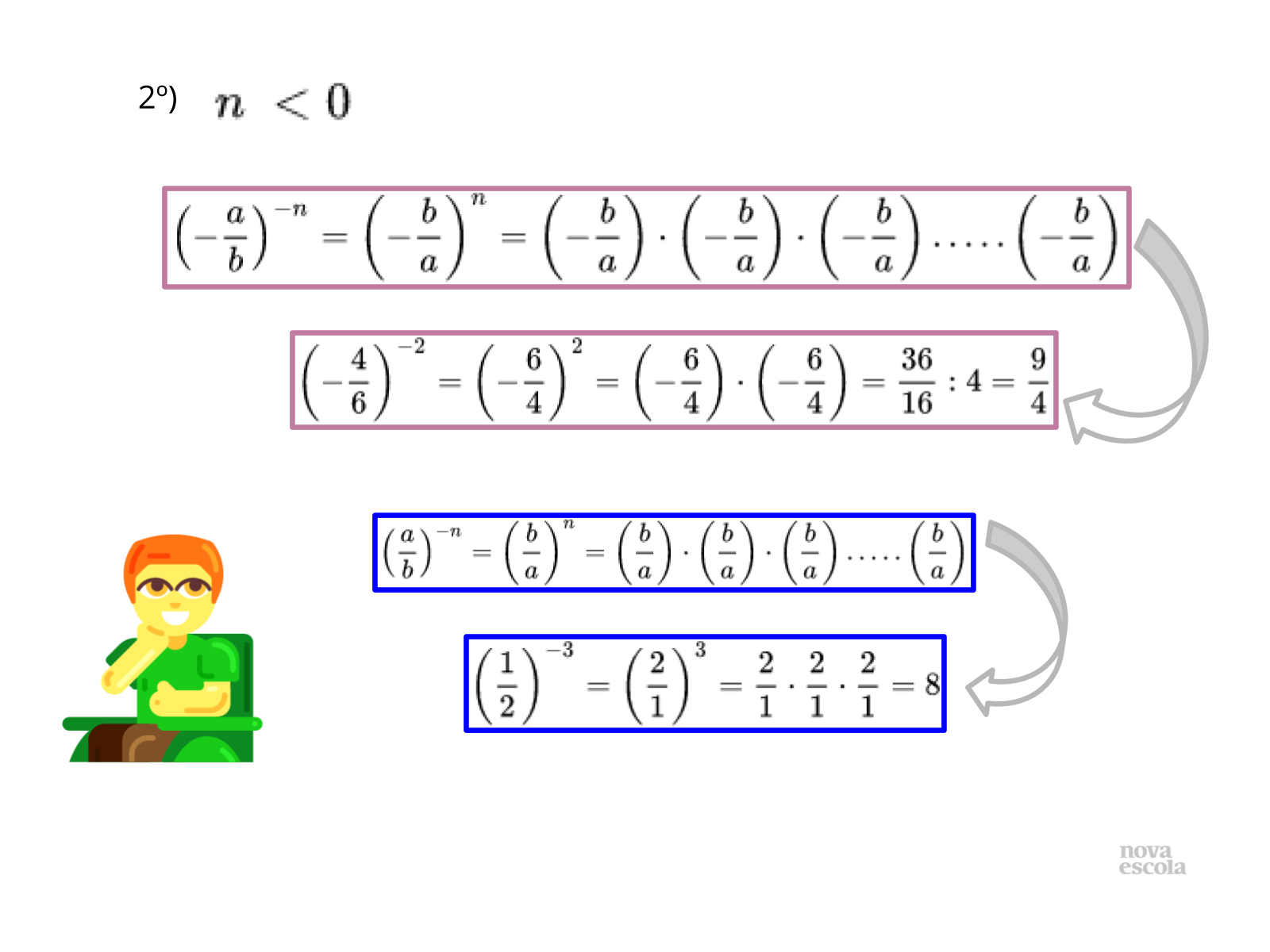
Orientação: Mostre aos alunos um algoritmo que funcione sempre. Explique que os números representados por a, b, c e d são inteiros, o que justifica o fato de os números racionais respeitarem a regra de sinal na multiplicação e divisão. Explique também que uma característica própria dos algoritmos é que devem funcionar para diversas situações.
Assim, quando multiplicamos por c x d os dois termos da fração a/b, obtemos uma fração equivalente onde os dois termos são múltiplos de c e d. Mostre isso para os alunos com exemplos.
Explique também que ao fazer a divisão, o “c” será cancelado no denominador e o “d” será cancelado no numerador. Assim, o resultado da divisão será sempre uma fração de numerador a x d e denominador b x c.
Propósito: descrever e fixar conceito referente ao conteúdo da aula: divisão de fracionários negativos e positivos.
Discuta com a turma:
- O que precisamos fazer para dividir um racional fracionário?
- E com os sinais, o que acontece?
- Podemos achar um “novo” resultado final? Como?
- Vocês conseguem identificar facilmente um número racional? Como?
Sistematização (slides 7 e 8)
Tempo sugerido: 3 min
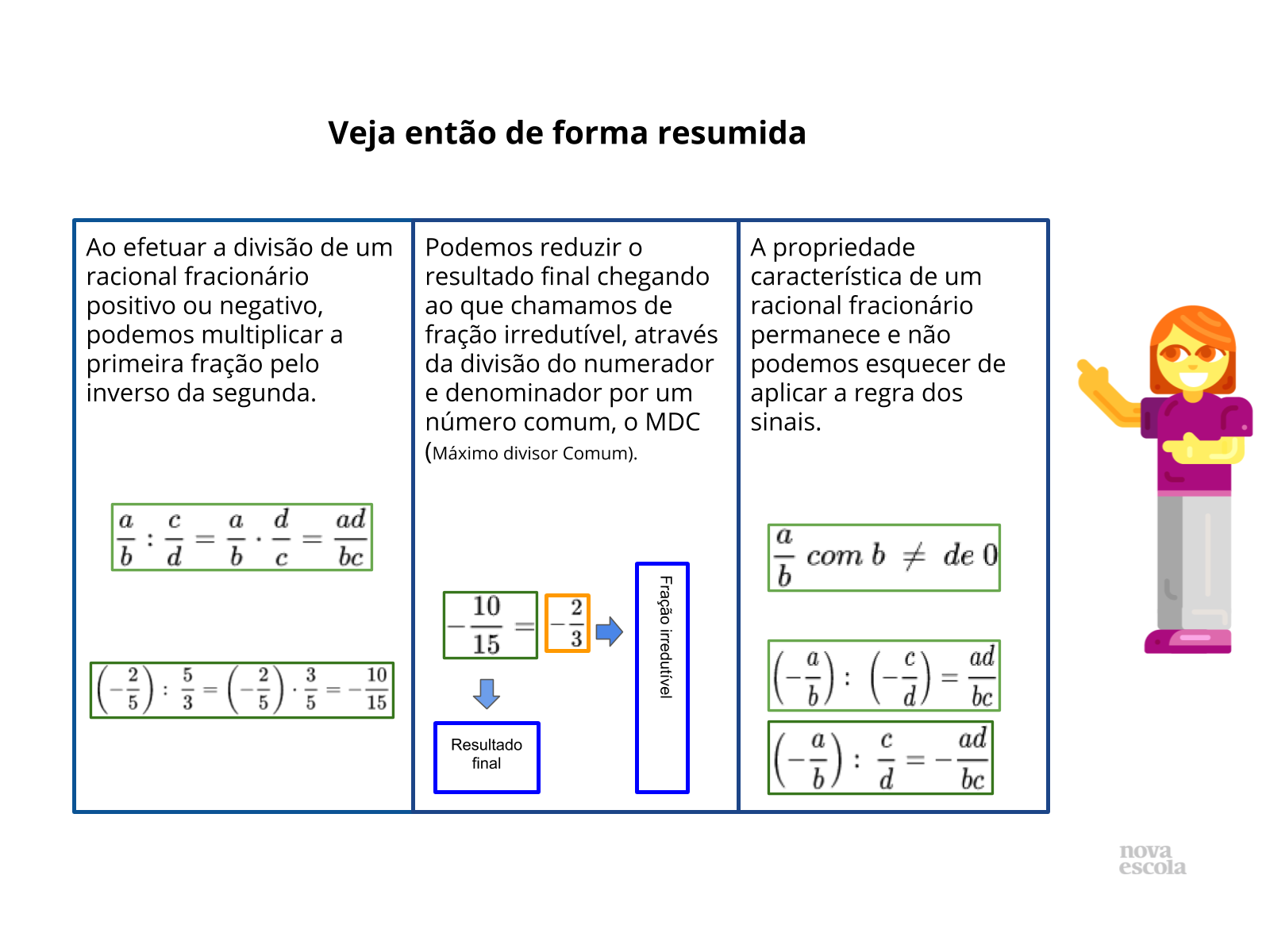
Orientação: Mostre aos alunos um algoritmo que funcione sempre. Explique que os números representados por a, b, c e d são inteiros, o que justifica o fato de os números racionais respeitarem a regra de sinal na multiplicação e divisão. Explique também que uma característica própria dos algoritmos é que devem funcionar para diversas situações.
Propósito: descrever e fixar conceito referente ao conteúdo da aula: divisão de fracionários negativos e positivos.
Discuta com a turma:
- O que precisamos fazer para dividir um racional fracionário?
- E com os sinais, o que acontece?
- Podemos achar um “novo” resultado final? Como?
- Vocês conseguem identificar facilmente um número racional? Como?
Raio X

Tempo sugerido: 7 min
Orientação: Imprima a atividade ou passe na lousa para que os alunos copiem. É essencial que cada um resolva a atividade individualmente para que seja possível verificar se os aprendizados foram concretizados.
Propósito: Avaliar a aprendizagem acerca do conceito de divisão de racionais na forma fracionária, positivos ou negativos.
Materiais complementares:
Para os Alunos
Para o Professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT7_08NUM03
Recursos
- caderno
- lápis
- grupo de alunos no WhatsApp
- Opcionais:
- Google Sala de Aula
- Zoom
- Vídeo: “Divisão de frações”- Khan Academy, disponível em: https://youtu.be/kvyY1lH_MTk, acesso em 23 de jun 2020.
Para este plano, foque na etapa: Atividade Principal
Aquecimento
O professor pode usar o Google Formulário para que os alunos respondam à atividade de retomada, seja digitando a resposta ou inserindo uma foto da resolução feita. Caso seja um trabalho sem recursos digitais, envie uma foto da atividade via WhatsApp para que os alunos possam resolver.
Atividade principal
Professor, para a realização da atividade principal os alunos precisam ter acesso ao problema proposto. Para isso, fotografe e disponibilize a imagem (no grupo de WhatsApp ou no Google Sala de Aula) para que os alunos possam pensar sobre ele. Peça que tentem resolver a atividade em dois momentos: no primeiro momento eles deverão pensar sozinhos sobre a situação proposta e anotar todas as suas estratégias de cálculo no caderno; no segundo momento, você pode sugerir que o aluno compartilhe a resposta com um familiar, e juntos discutam as estratégias de resolução. Oriente-os a fotografar as suas estratégias e respostas para compartilhar com o professor e a turma no momento da discussão das soluções.
Discussão das soluções
A discussão das soluções da atividade é uma etapa importantíssima da aula. É o momento de justificar as estratégias e respostas usadas para a resolução do problema proposto na atividade principal. Os alunos devem postar seus vídeos ou fotografias para compartilhar suas respostas em um ambiente de interação (como WhatsApp ou Google Sala de Aula, por exemplo). A intenção é formar um painel de soluções e promover uma discussão rica e estimuladora entre os alunos e professor. Neste momento estimule a turma a falar (usando a ferramenta de áudio ou vídeo) como pensou para resolver o problema, medie a conversa com os questionamentos propostos no slide. Estimule a turma a perceber que, para conhecer uma solução, podemos seguir por diversos caminhos, e que o erro é uma importante ferramenta para o ensino-aprendizagem, combatendo a valorização excessiva da resposta certa.
Encerramento
Convide os alunos a assistirem ao vídeo “Divisão de frações” do Khan Academy para o fechamento do assunto.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Rosiane F. Prates
Mentora: Débora Vieira de Moraes
Revisor: Rodrigo Morozetti Blanco
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA08 - Conceituar, relacionar aplicação dos números racionais dentro da divisão, desenvolver habilidades estratégicas de cálculo entre os racionais.
Conhecimentos que a turma deve dominar:
Domínio do conceito de fração, identificar a relação entre os conjuntos numéricos (racionais, inteiros e naturais); quatro operações com inteiros, comparação, diferenciação entre inteiro e fração.
Objetivos específicos
- Identificar os racionais fracionários positivos e negativos;
- realizar divisão com racionais fracionários positivos e negativos.
Conceito-chave
Divisão com racionais.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
- Projetor multimídia (caso não se utilize impressões)