Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
OBJETIVO

Tempo sugerido: 2 min
Orientação:
Antes de iniciar a aula divida a turma em grupos de dois ou três alunos, para que possam discutir entre si as soluções da atividade. Projete o objetivo ou copie na lousa.
Propósito: Apresentar para turma o objetivo da aula.
AQUECIMENTO.

Tempo sugerido: 5 min
Orientação:
Aguarde os alunos discutirem entre si para posteriormente exporem intuitivamente o que eles lembram sobre eventos. Anote na lousa as respostas dadas pelos alunos. A fim de fazer um parâmetro referente às respostas dadas por eles, utilize a seguinte situação: “Ao jogar uma moeda, qual a probabilidade de sair coroa?” Observe com os alunos que o espaço amostral é: {cara, coroa} e que o evento é aquilo que se espera, isto é, {sair coroa}. Questione aos alunos: se jogássemos duas moedas, sair coroa na segunda depende do que acontece com a primeira moeda? Espera-se que os alunos respondam que não, desse modo caracterizando eventos independentes. Posteriormente questione aos alunos: se soubéssemos que tenha caído cara na primeira moeda, qual a probabilidade de sair cara duas vezes? Neste caso estamos falando de eventos dependentes, uma vez que temos um evento condicionado.
Propósito: Mobilizar os conceitos sobre eventos.
ATIVIDADE PRINCIPAL

Tempo sugerido: 10 min.
Orientação:
Circule pela sala auxiliando os alunos, e questionando-os acerca do procedimento utilizado para a resolução.
Após os alunos realizarem a discussão em grupo, peça para que exponham suas resoluções para os colegas e instigue-os a concordarem ou discordarem e o motivo, a fim de chegarem a um consenso. Se necessário solicite aos alunos que façam a solução na lousa, tomando o cuidado de selecionar soluções distintas.
Lembre-os sobre as formas de representar os elementos do conjunto de combinações, utilizando-se de colchetes, ou árvores de possibilidades. Oriente os alunos a usarem a primeira letra de cada canal, para representar o evento, por exemplo: desenho (D), jornal (J) e filme (F).
Propósito: Fazer com que os alunos discutam entre si formas de solucionar a situação problema, utilizando-se de conceitos prévios de espaço amostral e distribuição de probabilidades.
Discuta com a turma:
Quais são os possíveis casos que podem acontecer? Ou seja, o espaço amostral.
O que acontece quando ocorre a reposição do papel?
DISCUSSÃO DAS SOLUÇÕES

Tempo sugerido: 13 min. (slides 5, 6, 7 e 8)
Orientação:
Peça aos alunos que exponham quais são os casos possíveis de acontecer, levando em consideração que serão sempre dois a dois. É importante deixar claro aos alunos que estamos construindo o espaço amostral. Caso os estudantes não consigam identificar o espaço amostral, tente auxiliá-los perguntando: Vocês conseguem me dizer que canal pode sair no primeiro papelzinho? E no segundo? Então podemos criar a primeira possibilidade, como (D,F).
Questione aos alunos quais foram as escolhas do Matheus, e, deste modo quantas possibilidades existem. Observe com os alunos que Matheus gostaria que saísse o canal de desenho e o de filme, nesta ordem. Ao questionar quais eventos são desejados, espera-se que os alunos respondam “sair desenho” e “sair filme” Deixe claro aos alunos que a ordem dos eventos é importante, uma vez que o irmão gostaria de assistir desenho no almoço e filme no jantar.
Questione aos alunos se a possibilidade (D,F) é igual a possibilidade (F,D)? Mostre aos alunos que neste caso a ordem é importante, portanto, tirar desenho e filme, não é o mesmo que tirar filme e desenho.
Propósito: Mostrar aos alunos uma das possibilidades de desenvolver a atividade atrelado ao conceito de evento.
Discuta com a turma:
Se colocarmos o papelzinho novamente, pode acontecer de Matheus sortear dois canais iguais?
Quais são os eventos desejados?
DISCUSSÃO DAS SOLUÇÕES

Tempo sugerido: 13 min. (slides 5, 6, 7 e 8)
Orientação:
Utilize as mesmas orientações do slide anterior, pois este é apenas uma continuação da discussão. Apresente esse slide apenas após os alunos discutirem suas soluções uns com os outros.
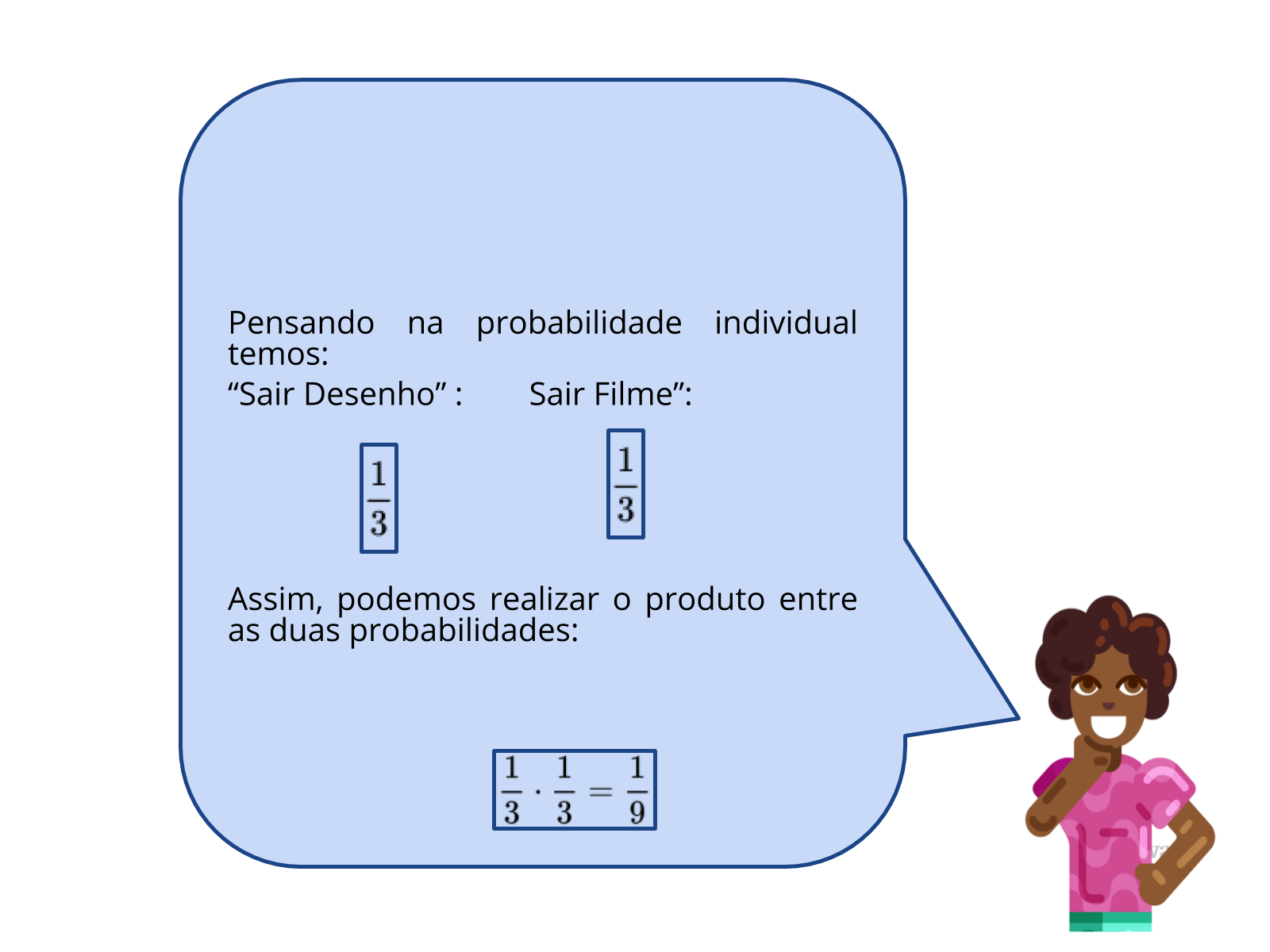
Observe que temos apenas uma opção dentre as nove que podem ser escolhidas. Desse modo espera-se que os alunos possam concluir que a probabilidade é de 1/9 . A partir de então, encaminhe a aula para o estudo do cálculo de probabilidades independentes. Questione aos alunos se eles conseguem identificar que os eventos “tirar um canal de desenho” e “tirar o canal de filmes” são independentes?
Propósito: Discutir com os alunos a partir das possibilidades o cálculo de probabilidade do evento esperado, além de atrelar ao conhecimento prévio de eventos dependentes e independentes.
Discuta com a turma
Sortear o evento “desenho” no primeiro sorteio interfere no sorteio do evento “filme” no segundo sorteio?
DISCUSSÃO DAS SOLUÇÕES

Tempo sugerido:13 min. (slides 5, 6, 7 e 8)
Orientação:
Diga aos alunos que o objetivo é fazer uma combinação de dois canais, assim podemos calcular a probabilidade individual de cada caso. Sabe-se que probabilidade de sair desenho no primeiro sorteio é 1 em 3 e repor o papelzinho no saquinho (o que quer dizer que o espaço amostral está inalterado) implica na probabilidade de sair “filme” no segundo sorteio também (probabilidade de 1 em 3). Lembrando do princípio multiplicativo, quando queremos fazer um combinação entre dois ou mais elementos nós fazemos o produto das possibilidades. No nosso caso, o produto entre as probabilidades. Assim, queremos a probabilidade de sair desenho no primeiro sorteio e filme no segundo: logo a probabilidade é ?* ? = 1/9 . Professor: espera-se que os alunos tenham domínio sobre soma de probabilidades.
Propósito: Discutir a conceitualização do produto de probabilidades.
Discuta com a turma:
Que forma vocês conhecem de calcular a probabilidade?
DISCUSSÃO E RESOLUÇÃO DA ATIVIDADE
Tempo sugerido: 13 min. (slides 5, 6, 7 e 8)
Orientação: Aqui é apenas a exposição da discussão do slide anterior.
Propósito: O mesmo do slide anterior.
ENCAMINHAMENTO 2 DA ATIVIDADE PRINCIPAL.
Tempo sugerido: 7 min
Orientação:
Lance o questionamento: Se ela retira o primeiro papelzinho, qual é a probabilidade de sair desenho? Espera-se que os alunos respondam que é 1 em 3. Mas ela não repôs o papel na segunda retirada, então qual é o novo espaço amostral? Desse modo a probabilidade do segunda retirada é 1 em 2. Assim aplicando o princípio multiplicativo, a probabilidade final é ? * ½ = ?
Observe com os alunos que agora estamos trabalhando com eventos dependentes, ou seja, a probabilidade do evento B {sair filme}, depende da primeira retirada.
Propósito: Observar a diferença entre os eventos dependentes e independentes e qual a relação entre eles e a alteração do espaço amostral.
Discuta com a turma:
Há alteração do espaço amostral quando não se tem reposição?
Neste caso, são eventos dependentes ou independentes?
SISTEMATIZAÇÃO
Tempo sugerido: 2min
Orientação:
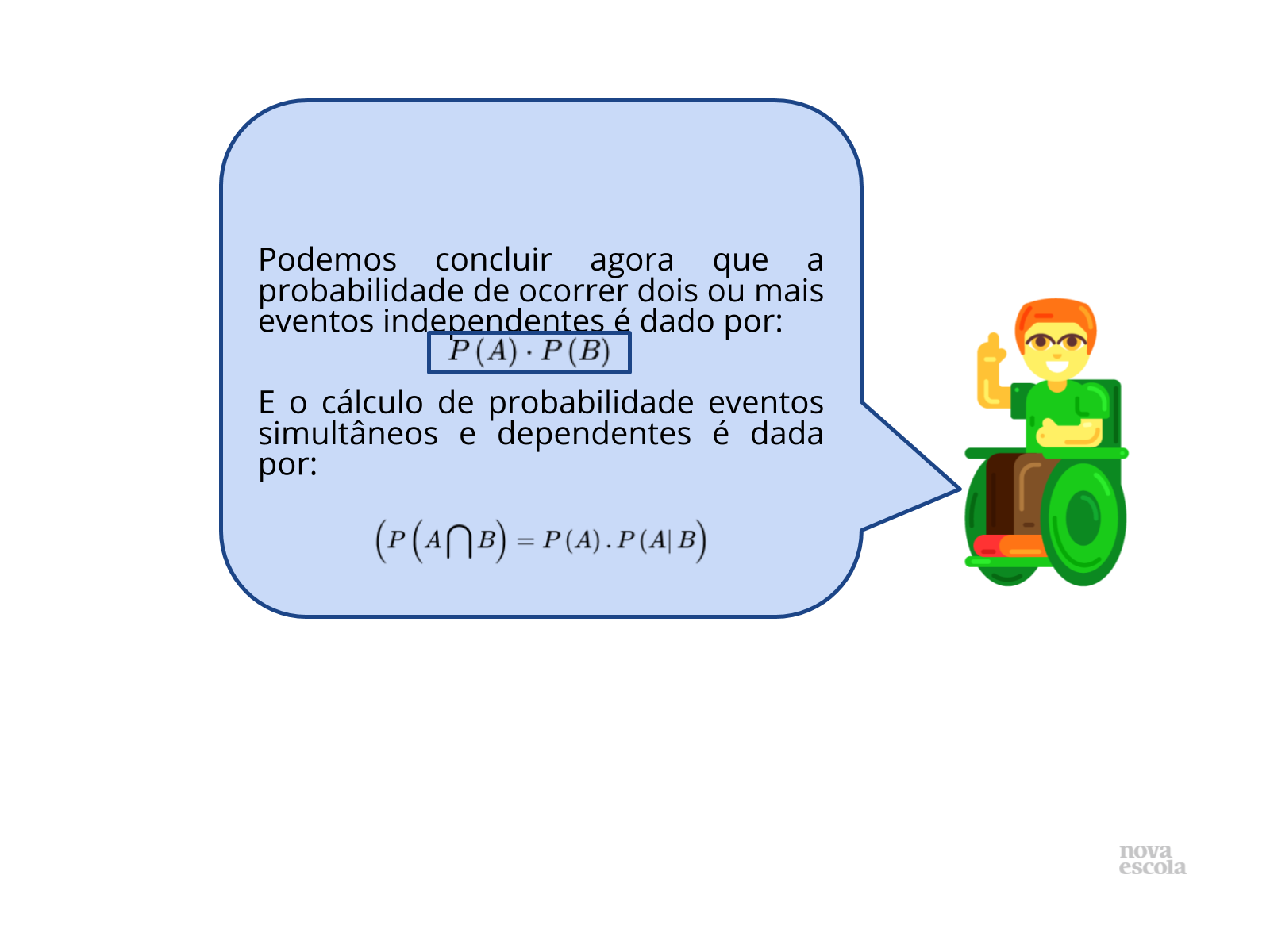
Ressaltar a turma que P(A|B) significa que é a probabilidade do evento A sabendo que B já aconteceu, ou seja, quando o segundo evento depende do primeiro.
Propósito: Sistematizar o conceito de produto de probabilidades para eventos dependentes e independentes.
Discuta com a turma:
O que são dois eventos simultâneos?
ENCERRAMENTO.

Tempo sugerido: 1 min.
Propósito: Concluir sobre cálculo de probabilidades de eventos dependentes e independentes.
RAIO-X.

Tempo sugerido: 10 min
Orientação: Professor, circule pela sala observando o andamento da resolução da atividade. Oriente aos alunos que discutam entre si as formas de resolver, observando primeiramente se são eventos dependentes ou independentes. Posteriormente incentivá-los para que exponham suas resoluções a classe para que todos possam discutir.
Propósito: Auxiliar os alunos a verificar as formas de cálculo de probabilidade de eventos independentes em um contexto, utilizando-se de cartas.
Discuta com a turma:
Os eventos são dependentes ou independentes?
O espaço amostral altera-se ao retirar cartas sucessivamente?
Qual das duas fórmulas utilizar?
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.