Resumo da Aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete o slide ou escreva no quadro o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 4 minutos.
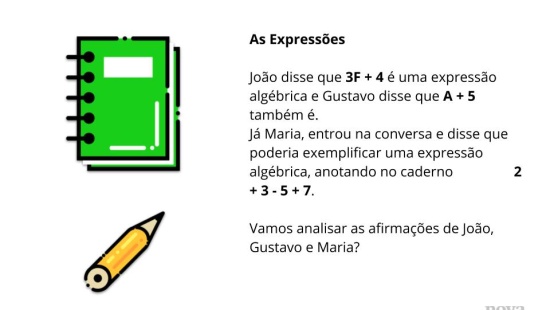
Orientações: Projete o slide no quadro ou leia juntamente com os alunos as informações contidas nele. Retome a ideia de expressão algébrica variável e o cálculo do valor numérico de uma expressão algébrica. Posteriormente, apresente para eles a expressão numérica do próximo slide. Dê um tempo para que eles calculem o resultado da expressão numérica e, a partir das resoluções dos alunos, relembre sobre as regras de resolução de uma expressão numérica quanto às operações (adição, subtração, multiplicação, divisão, potenciação e radiciação), e quanto aos símbolos (parênteses, colchetes e chaves).
Na expressão numérica utilizada como exemplo, se atente ao fato de que quando um numérico é seguido imediatamente por um destes símbolos operatórios, a operação de MULTIPLICAÇÃO está implícita.
Propósito: Retomar o conceito de valor numérico de uma expressão algébrica e as regras de resolução de uma expressão numérica quanto às operações (adição, subtração, multiplicação, divisão, potenciação e radiciação), e quanto aos símbolos (parênteses, colchetes e chaves).
Atividade Principal </tiltle>

Atividade Principal
Tempo sugerido: 25 minutos. (Slides 4, 5, 6, 7, 8 e 9)
Orientações: Distribua as atividades impressas ou projete o slide no quadro, e leia juntamente com os alunos o problema da situação número 1. Tire as possíveis dúvidas de interpretação. Neste momento, os alunos devem, individualmente, analisar e pensar em uma forma de solucionar o problema. Utilize o Guia de Intervenções para analisar dificuldades e realizar intervenções.
É provável (esperamos que sim), que algum aluno discorde da forma como a expressão algébrica foi apresentada para a situação. Ele(a) poderá sugerir (C-2): 20 (Sim! O “C”é para o mesmo propósito do “x”; a indicação da variável aqui tanto faz), e não estará errado! Argumente que nesta proposta de expressão algébrica, para não confundir o significado e por ventura achar que o 2 seria dividido por 20 { C - 2 :20 } , até porque a DIVISÃO tem PRIORIDADE sobre a SUBTRAÇÃO, o uso dos parênteses foi necessário, este é o propósito! Esta mesma interpretação poderá ocorrer na situação 2. Se ninguém se manifestar, faça você mesmo esta observação pertinente. Caso alguém faça, elogie a atitude.
Propósito: Fazer com que os alunos compreendam a importância da organização do raciocínio matemático, através do uso de símbolos organizatórios, como no caso, os parênteses.
Discuta com a Turma:
- Supondo que, inicialmente, os alunos não reconheçam a hierarquia dos sinais operatórios, deixe que argumentem a concordância ou não com a expressão algébrica dada. O que foi pensado? De maneira chegou-se a essa ideia?
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal

Tempo sugerido: 25 minutos. (Slides 4, 5, 6, 7, 8 e 9)
Orientações: Distribua as atividades impressas ou projete o slide no quadro, e leia juntamente com os alunos o problema da situação 2. Tire as possíveis dúvidas de interpretação. Neste momento, os alunos devem, individualmente, analisar e pensar em uma forma de solucionar o problema. Utilize o Guia de Intervenções (o link pode pode ser encontrado nos Materiais Complementares, ao final das Orientações ao Professor), para analisar dificuldades e realizar intervenções.
Não esqueça a observação sobre outros pontos de vistas, indicado o slide anterior.
Propósito: Fazer com que os alunos compreendam a importância da organização do raciocínio matemático, através do uso de símbolos organizatórios, como no caso, os parênteses.
Discuta com a Turma:
- Supondo que, inicialmente, os alunos não reconheçam a hierarquia dos sinais operatórios, deixe que argumentem a concordância ou não com a expressão algébrica dada. O que foi pensado? De maneira chegou-se a essa ideia?
Atividade Principal

Tempo sugerido: 25 minutos. (Slides 4, 5, 6, 7, 8 e 9)
Orientações: Deixe que apontem livremente as semelhanças e as diferenças entre as duas expressões. É possível que algum(s) aluno(s) se atentem somente à expressão algébrica, sem correlacioná-las com as situações 1 e 2. Neste caso, a única diferença é a variável, que em uma é “x” e em outra, “y”. Se algum aluno sugerir que as duas expressões poderiam ser escritas na mesma variável, diga que não explique que cada uma representa uma situação diferente e que os valores envolvidos em uma não são iguais na outra.
É importante que não se apresente as expressões com outra forma de escrita, como por exemplo, x/20 +2, porque neste caso, ficará claro a hierarquia das operações e o objetivo da situação se torna nula. Pode-se sim, ao final da discussão de toda a Atividade Principal, apontar esta forma de escrita como estratégia de evitar erros de interpretação da expressão algébrica.
Propósito: Fazer com que os alunos compreendam a importância da organização do raciocínio matemático, através do uso de símbolos organizatórios, como no caso, os parênteses.
Discuta com a Turma:
- Como vocês conseguiram encontrar a quantidade de balas em cada situação?
- Como distribuir os parênteses para as duas situações?
- Qual foi a lógica que usaram para identificarem a posição dos parênteses em cada expressão algébrica?
- Como conseguiram encontrar a quantidade de balas em cada situação?
- Como distribuir os parênteses para as duas situações?
- Qual foi a lógica que usaram para identificarem a posição dos parênteses em cada expressão algébrica?
Atividade Principal

Tempo sugerido: 25 minutos. (Slides 4, 5, 6, 7, 8 e 9)
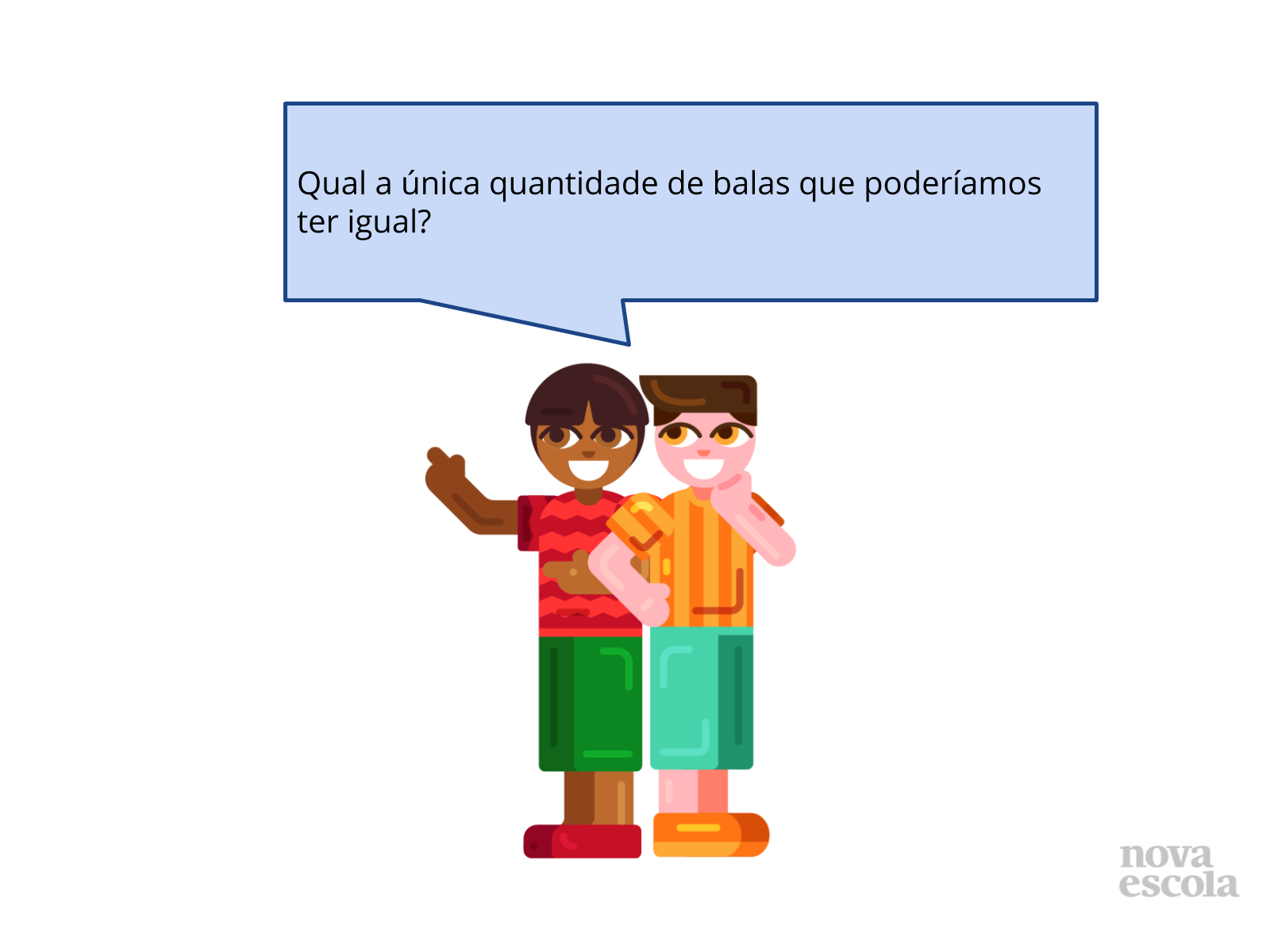
Orientações: Uma vez que os alunos já identificaram as diferenças e conseguem apontar a posição dos parênteses nas duas expressões, a saber, Situação 1: (x /20) +2 e Situação 2: x/(20 + 2), então dê-lhes um pequeno tempo (sugerido 1 minuto), para poderem responder a pergunta. Lembre-lhes que o Cauê tem seu problema descrito pela Situação 2. Logo após, se tiver distribuído a sala em duplas, peça a uma das duplas para apontar seu raciocínio. Caso esta dupla tenha calculado errado, ainda assim os deixe explicar todo o seu raciocínio e se tiver tempo, peça a outra dupla que apresentou resultado diferente para discutir as formas de resolução.
Não deixe que o aluno que “errou” o resultado se sinta desmotivado ou à margem da discussão. É importante, também, que não o deixe desmanchar sua resposta, e sim, oriente-o a manter as duas resoluções e se possível, com um comentário do ponto onde cometeu o equívoco.
Propósito: Fazer com que os alunos compreendam a importância da organização do raciocínio matemático, através do uso de símbolos organizatórios, como no caso, os parênteses.
Discuta com a turma:
- Como conseguiram encontrar as possíveis quantidades de balas na situação?
- Conseguem visualizar algum padrão comportamental?
Atividade Principal

Tempo sugerido: 25 minutos. (Slides 4, 5, 6, 7, 8 e 9)
Orientações: Uma vez que os alunos já identificaram as diferenças e conseguem apontar a posição dos parênteses nas duas expressões, a saber, Situação 1: (x /20) +2 e Situação 2: x/(20 + 2), então dê-lhes um pequeno tempo (sugerido 1 minuto), para poderem responder a pergunta. Lembre-lhes que o Guilherme tem seu problema descrito pela Situação 1. Logo após, se tiver distribuído a sala em duplas, peça a uma das duplas para apontar seu raciocínio. Caso esta dupla a tenha calculado errado, ainda assim, deixe-os explicar todo o seu raciocínio e se tiver tempo, peça a outra dupla que apresentou resultado diferente para discutir as formas de resolução.
Não deixe que o aluno que “errou” o resultado se sinta desmotivado ou à margem da discussão. É importante, também, que não o deixe desmanchar sua resposta, e sim, oriente-o a manter as duas resoluções e se possível, com um comentário do ponto onde cometeu o equívoco.
Propósito: Fazer com que os alunos compreendam a importância de organização do raciocínio matemático, através do uso de símbolos organizatórios, como no caso, os parênteses.
Discuta com a Turma:
- Como conseguiram encontrar as possíveis quantidades de balas na situação?
- Conseguem visualizar algum padrão comportamental?
title> Atividade Principal
title> Atividade Principal
Tempo sugerido: 25 minutos. (Slides 4, 5, 6, 7, 8 e 9)
Orientações: Uma vez que os alunos já identificaram as diferenças e conseguem apontar a posição dos parênteses nas duas expressões, a saber, Situação 1: (x /20) +2 e Situação 2: x/(20 + 2), então dê-lhes um pequeno tempo (sugerido 1 minuto), para poderem responder a pergunta. Lembre-lhes que o Guilherme tem seu problema descrito pela Situação 1. Logo após, se tiver distribuído a sala em duplas, peça a uma das duplas para apontar seu raciocínio. Caso esta dupla a tenha calculado errado, ainda assim, deixe-os explicar todo o seu raciocínio e se tiver tempo, peça a outra dupla que apresentou resultado diferente para discutir as formas de resolução.
Não deixe que o aluno que “errou” o resultado se sinta desmotivado ou à margem da discussão. É importante, também, que não o deixe desmanchar sua resposta, e sim, oriente-o a manter as duas resoluções e se possível, com um comentário do ponto onde cometeu o equívoco.
Propósito: Fazer com que os alunos compreendam a importância de organização do raciocínio matemático, através do uso de símbolos organizatórios, como no caso, os parênteses.
Discussão das Soluções

Tempo sugerido: 12 minutos. (Slides 10 e 11).
Orientações: Apresente as soluções e depois discuta com os alunos a forma que eles resolveram a questão e busque mostrar que existem diversas formas de solução e que eles não devem ficar presos a uma delas somente. Utilize o Guia de Intervenções para analisar dificuldades e realizar intervenções.
Propósito: Fazer com que os alunos observem as diversas formas de resolução e corrijam possíveis erros.
Discuta com a turma:
- Como vocês conseguiram encontrar a quantidade de balas em cada situação?
- Como distribuir os parênteses para as duas situações?
- Qual foi a lógica que usaram para identificar a posição dos parênteses em cada expressão algébrica?
Discussão das Soluções

Tempo sugerido: 12 minutos. (Slides 10 e 11).
Orientações: Apresente as soluções e depois discuta com os alunos a forma que eles resolveram a questão e busque mostrar que existem diversas formas de solução e que eles não devem ficar presos a uma delas somente. Utilize o Guia de Intervenções para analisar dificuldades e realizar intervenções.
Propósito: Fazer com que os alunos observem as diversas formas de resolução e corrijam possíveis erros.
Discuta com a turma:
- Como vocês conseguiram encontrar a quantidade de balas em cada situação?
- Como distribuir os parênteses para as duas situações?
- Qual foi a lógica que usaram para identificar a posição dos parênteses em cada expressão algébrica?
Encerramento

Tempo sugerido: 3 minutos.
Orientações: Leia o texto com os alunos e busque associar os exercícios da Atividade Principal com os tópicos apresentados. Diga-lhes da importância da organização do raciocínio para a boa aplicação da matemática.
Propósito: Fazer com que os alunos observem o que foi aprendido na aula.
Raio X

Tempo sugerido: 4 minutos.
Orientações: Distribua as atividades impressas ou projete o slide no quadro e peça para que os alunos leiam e resolvam a questão. Ajude os alunos que estiverem com dúvida, mas lembre-se de não dar a resposta para eles, mas faça-os pensarem na solução sozinhos.
Propósito: Verificar se os alunos conseguiram absorver o conhecimento da aula e conseguem aplicá-lo neste exercício. A partir do resultado deste exercício, você poderá avaliar se os alunos atingiram o objetivo desta aula e pensar em uma intervenção total ou parcial do conteúdo, se necessário.
Materiais complementares para impressão:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar



 Atividade Principal
Atividade Principal 



 title> Atividade Principal
title> Atividade Principal