Resumo da aula.
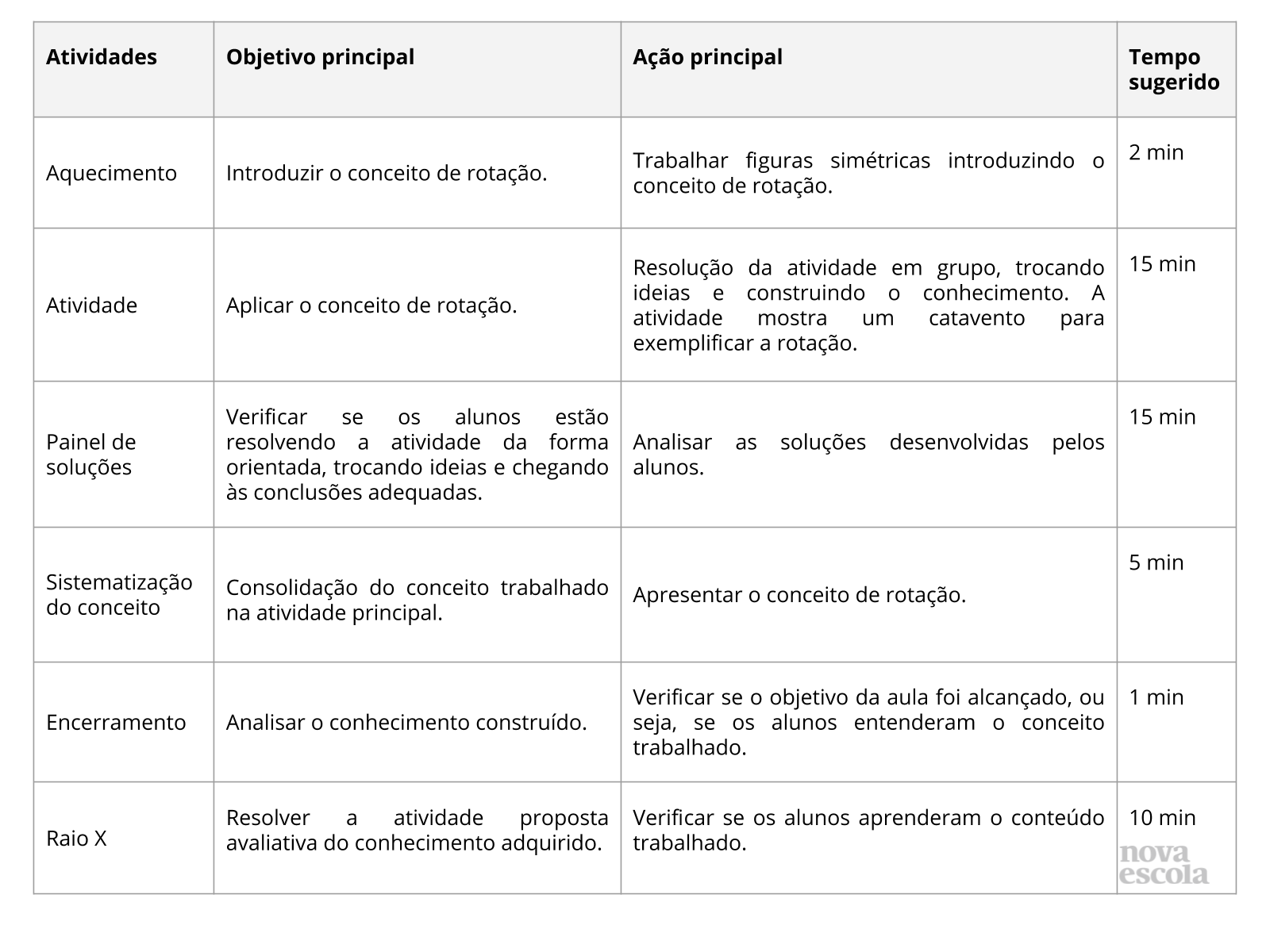
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
OBJETIVO.

Tempo sugerido: 2 minutos
Orientação: Compartilhar com a turma o objetivo da aula.
Propósito: Apresentar o objetivo da aula para a turma.
Aquecimento
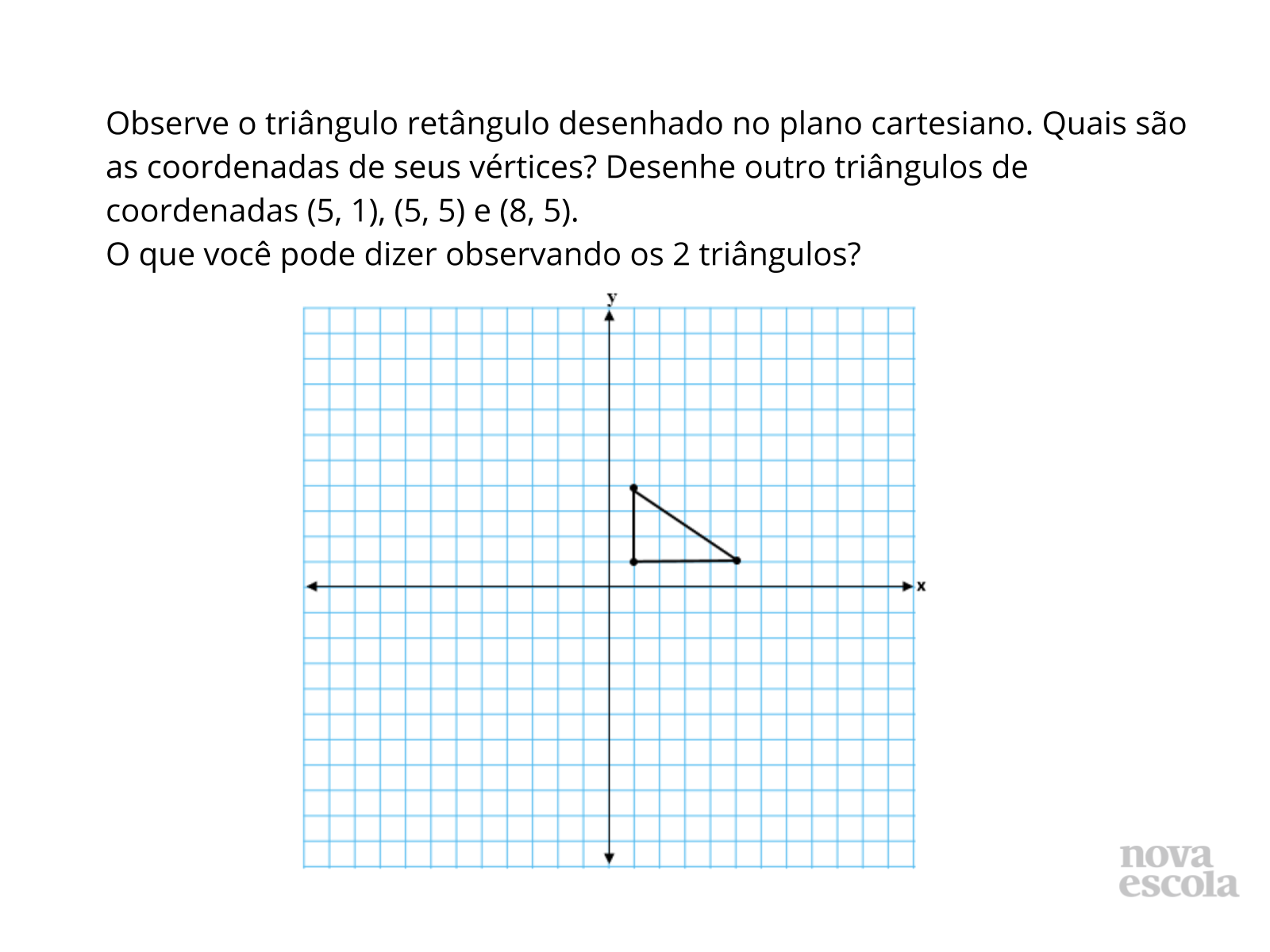
Tempo sugerido: 2 minutos.
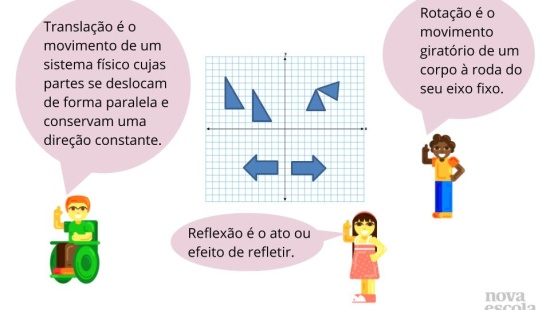
Orientação: Conversar com os alunos sobre simetria, abordar que duas figuras simétricas possuem mesmo formato e tamanho. Falar sobre os diferentes tipos de isometria. Perguntar o que vem à cabeça quando falamos a palavra rotação. Pedir exemplos de rotação (relógio, catavento, liquidificador, ventilador, etc.). Fazendo a atividade os alunos deverão perceber que os dois triângulos são simétricos, possuem mesmo formato e tamanho. Contudo, o triângulo apenas girou, isso é rotação.
Você encontra a atividade de aquecimento para impressão no link atividade de aquecimento. Você terá acesso à resolução desta atividade clicando no link resolução da atividade de aquecimento.
Propósito: Introduzir o conceito de rotação.
Atividade principal.

Tempo sugerido: 15 minutos
Orientação: Dividir a turma em trios e solicitar que cada um faça a rotação de um dos 3 pontos do triângulo. Dar nome aos 3 vértices do triângulo (A, B e C). Chamar de A o ponto que está fixado no palito. Rotacionar os pontos B e C. Professor, apesar da questão solicitar que o aluno faça apenas mais uma pá do catavento, se tiver tempo hábil na sua aula, você poderá solicitar que o aluno faça as outras duas para que o catavento fique completo. Se não houver tempo, você também poderá solicitar que o aluno termine em casa e mostre o catavento completo na próxima aula.
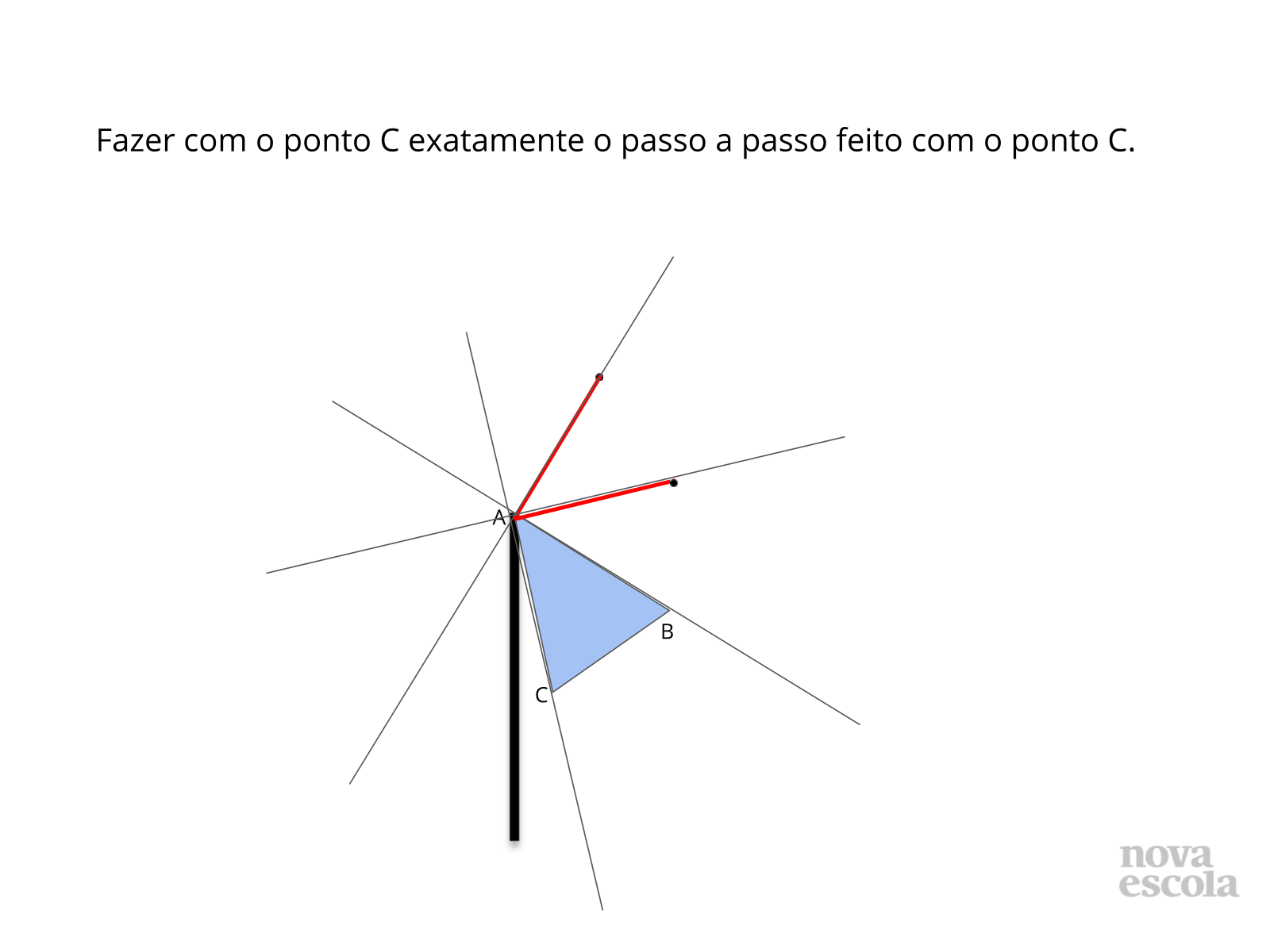
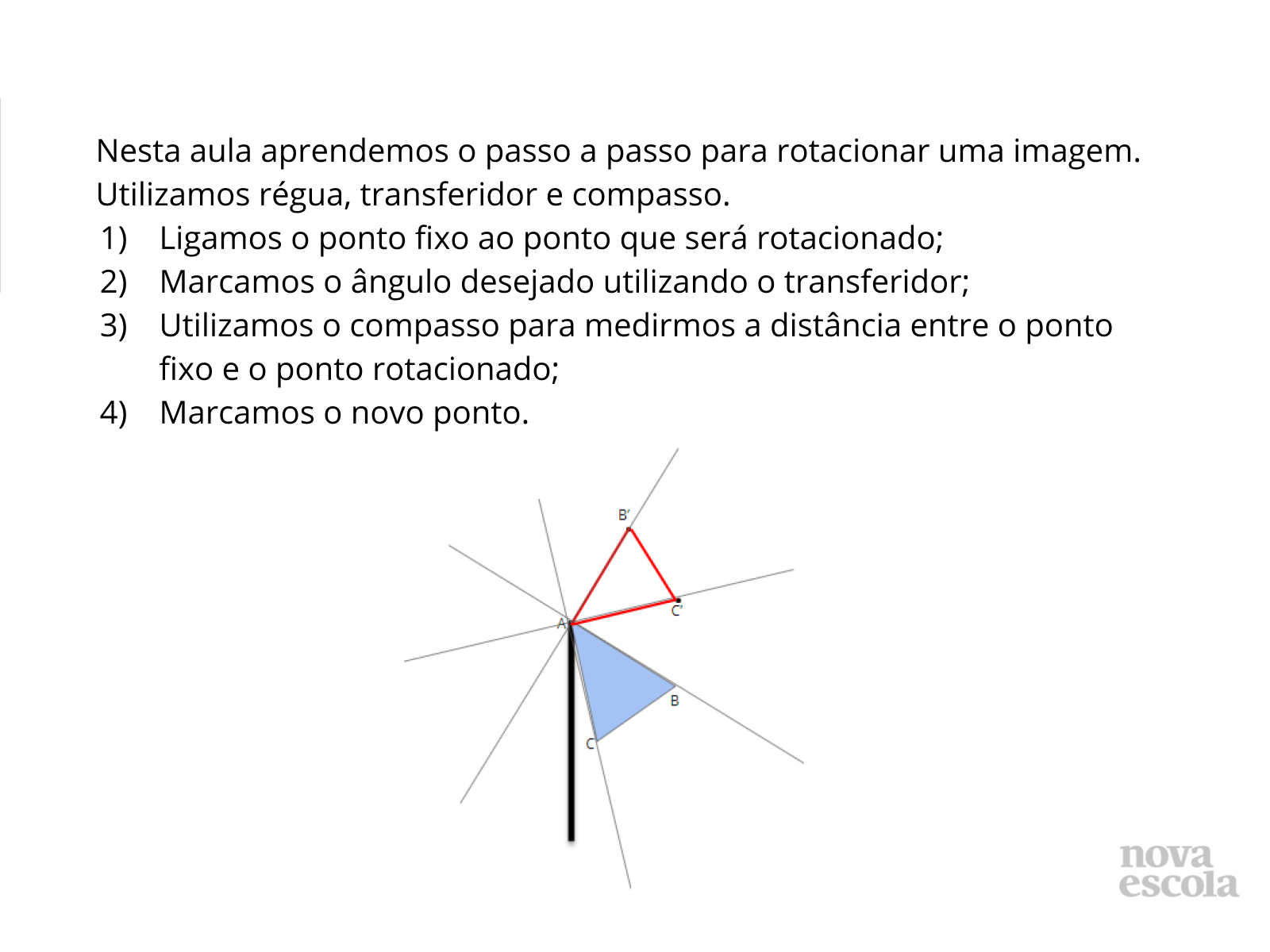
Nesta aula aprenderemos o passo a passo para rotacionar uma imagem. Utilizaremos régua, transferidor e compasso.
- Ligamos o ponto fixo ao ponto que será rotacionado;
- Marcamos o ângulo desejado utilizando o transferidor;
- Utilizamos o compasso para medirmos a distância entre o ponto fixo e o ponto rotacionado;
- Marcamos o novo ponto.
Propósito: Aprender a aplicar a simetria de rotação.
Discuta com a turma:
1) Qual é o primeiro passo para rotacionar o ponto B?
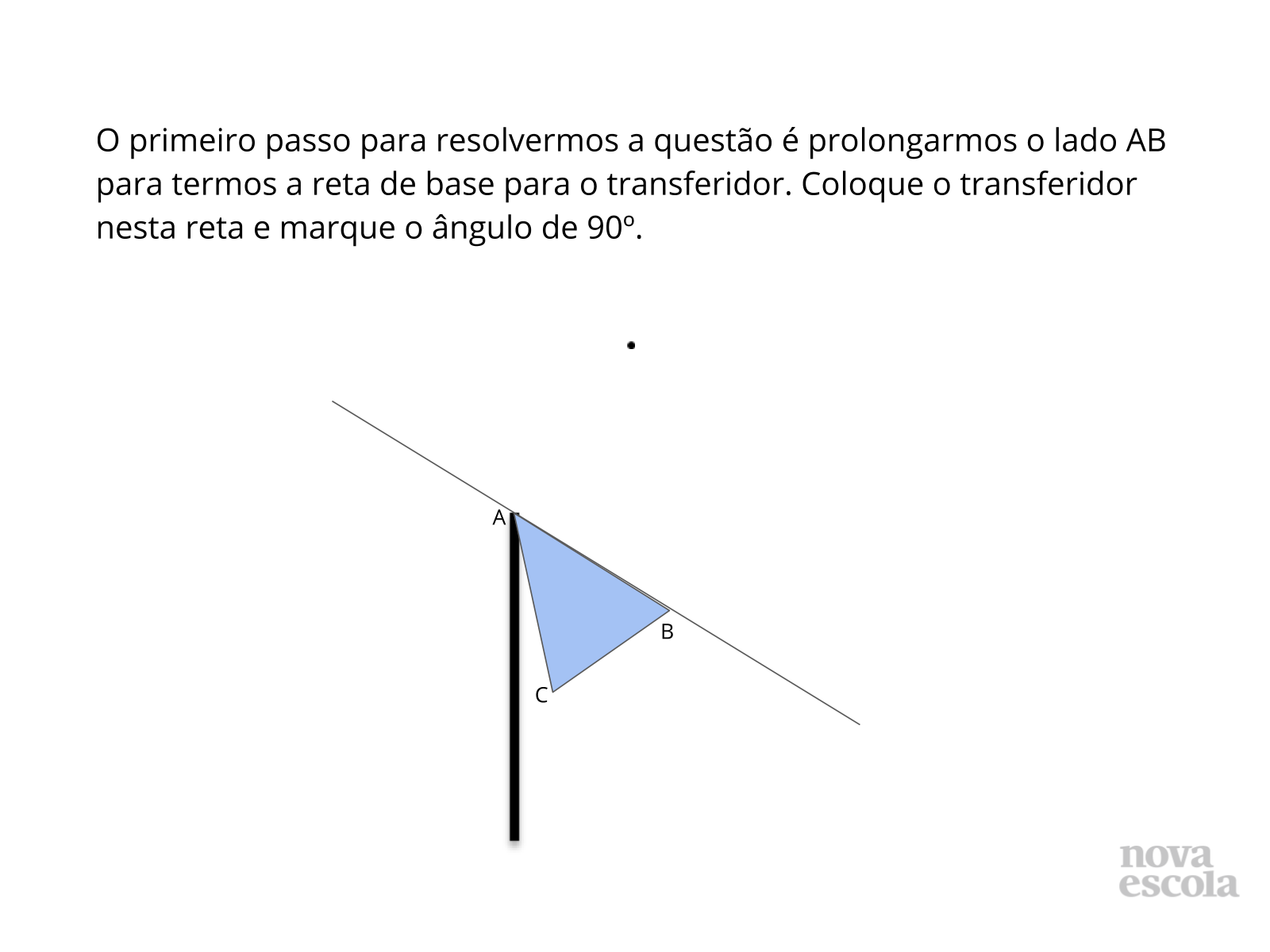
2) Após ligarmos o ponto B ao ponto A, prolongando a reta para servir de suporte para o transferidor, o que devemos fazer?
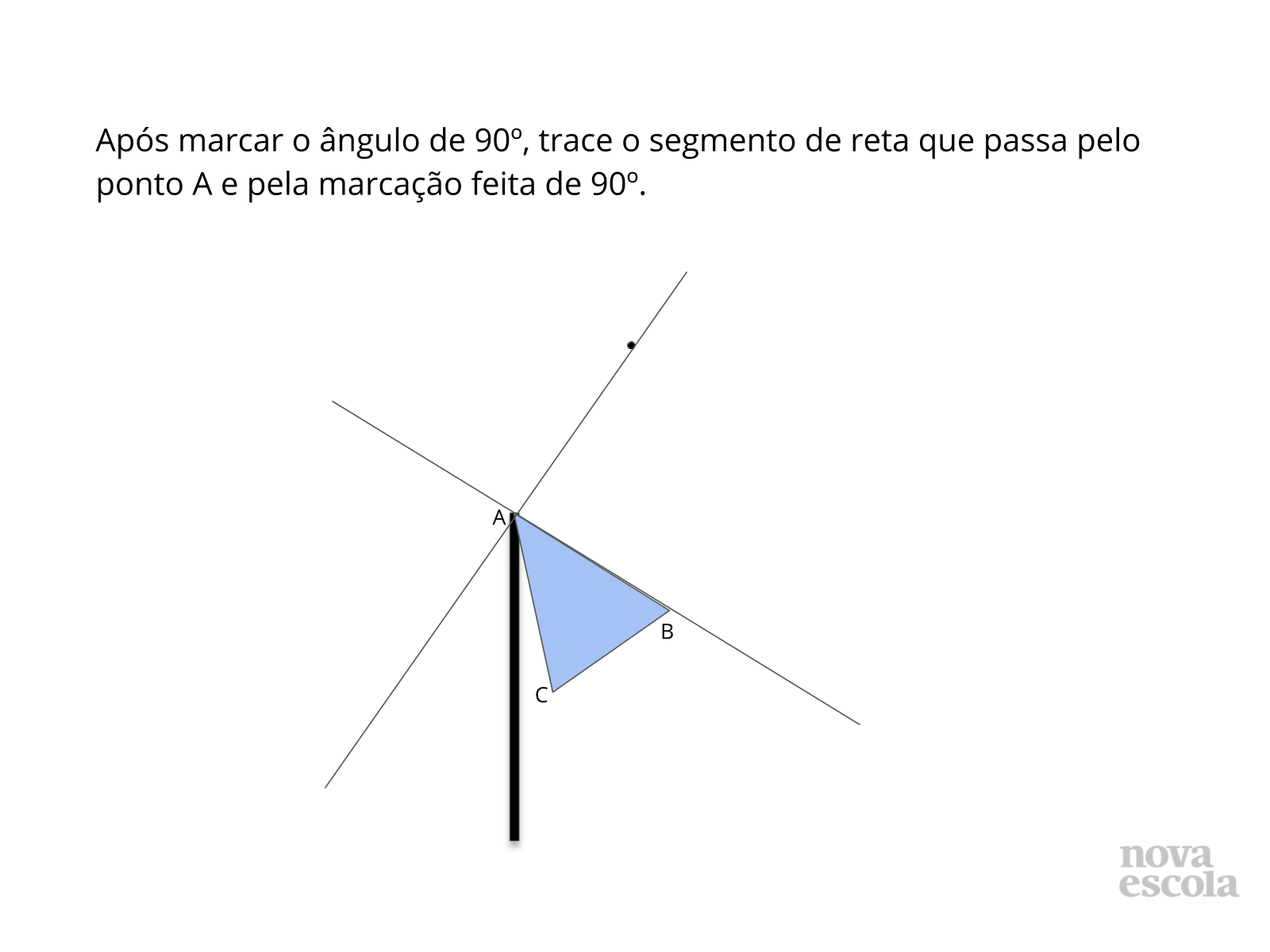
3) Após marcarmos o ângulo de 90º sobre a reta BA, o que devemos fazer?
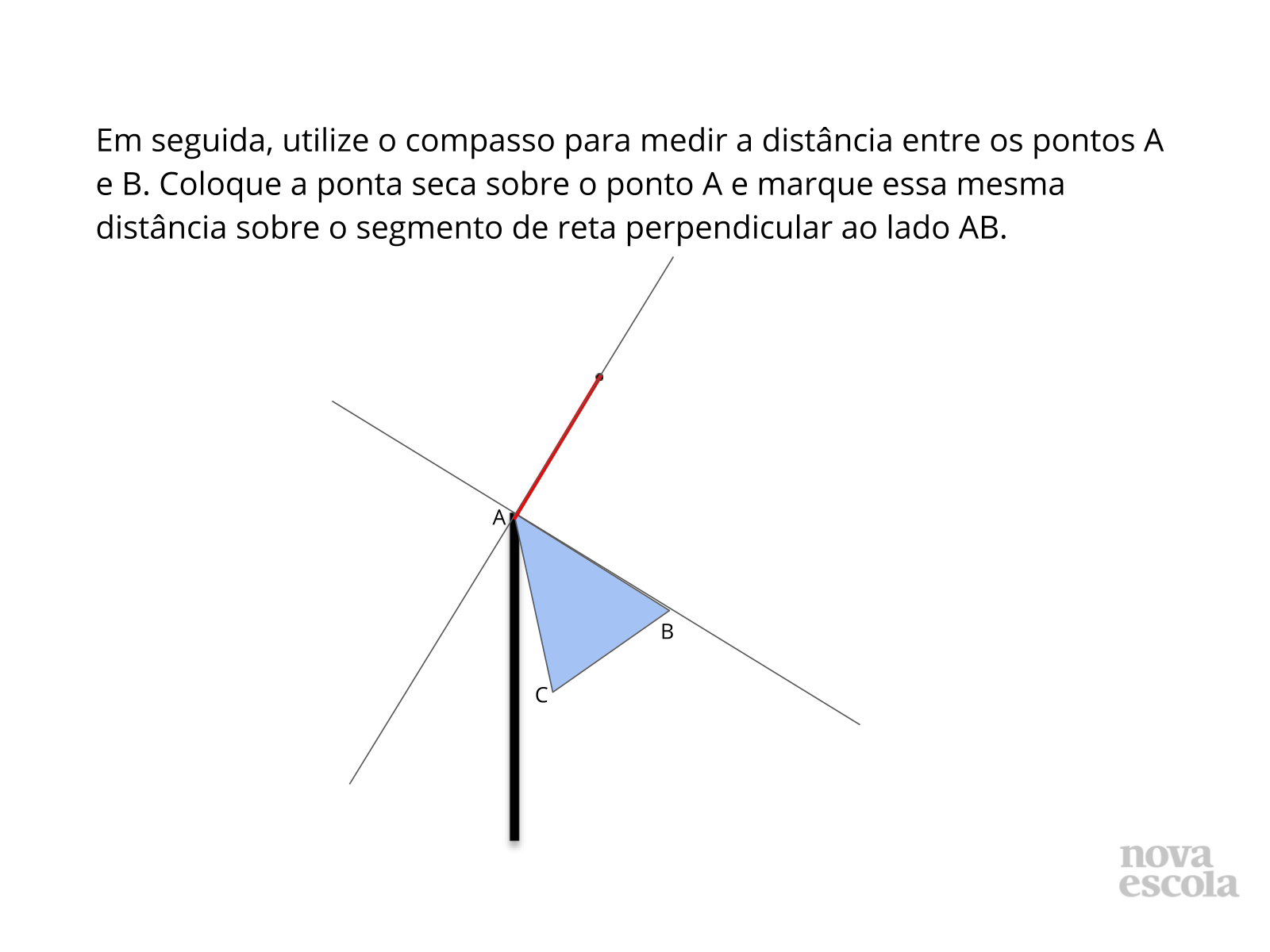
4) Após verificarmos, com o compasso, a distância entre os pontos B e A e marcarmos essa distância no novo segmento desenhado, podemos proceder da mesma forma para rotacionar o ponto C?
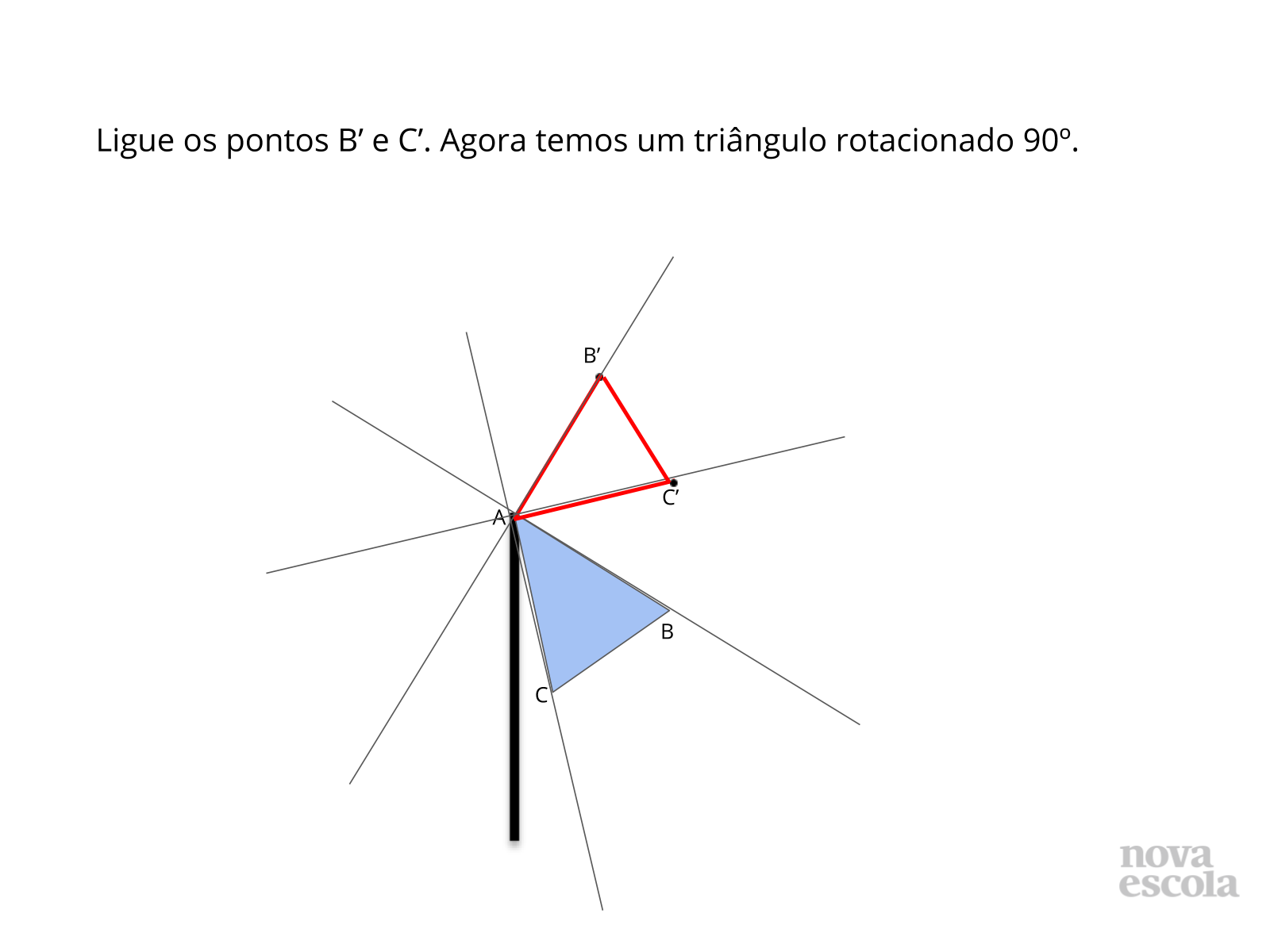
5) Marcados os pontos B’ e C’, basta ligarmos os novos pontos para termos o triângulo rotacionado 60º no entorno do ponto A?
Discussão da solução.
Tempo sugerido: 15 minutos (slides 5 a 9)
Orientação: Solicitar que em duplas a turma discuta a questão. Cada aluno da dupla pode fazer a rotação de um dos 2 vértices necessários do triângulo.
Propósito: Levar o aluno a pensar como determinar os simétricos de um ponto.
Discuta com a turma:
1) Qual é o primeiro passo para rotacionar o ponto B?
2) Após ligarmos o ponto B ao ponto A, prolongando a reta para servir de suporte para o transferidor, o que devemos fazer?
3) Após marcarmos o ângulo de 90º sobre a reta BA, o que devemos fazer?
4) Após verificarmos, com o compasso, a distância entre os pontos B e A e marcamos essa distância no novo segmento desenhado, podemos proceder da mesma forma para rotacionar o ponto C?
5) Marcados os pontos B’ e C’, basta ligarmos os novos pontos para termos o triângulo rotacionado 60º no entorno do ponto A?
Propósito: Levar o aluno a pensar como determinar os simétricos de um ponto.
Discussão da solução.
Tempo sugerido: 15 minutos (slides 5 a 9)
Orientação: Solicitar que em duplas a turma discuta a questão. Cada aluno da dupla pode fazer a rotação de um dos 2 vértices necessários do triângulo.
Propósito: Levar o aluno a pensar como determinar os simétricos de um ponto.
Discuta com a turma:
1) Qual é o primeiro passo para rotacionar o ponto B?
2) Após ligarmos o ponto B ao ponto A, prolongando a reta para servir de suporte para o transferidor, o que devemos fazer?
3) Após marcarmos o ângulo de 90º sobre a reta BA, o que devemos fazer?
4) Após verificarmos, com o compasso, a distância entre os pontos B e A e marcamos essa distância no novo segmento desenhado, podemos proceder da mesma forma para rotacionar o ponto C?
5) Marcados os pontos B’ e C’, basta ligarmos os novos pontos para termos o triângulo rotacionado 60º no entorno do ponto A?
Propósito: Levar o aluno a pensar como determinar os simétricos de um ponto.
Discussão da solução.
Tempo sugerido: 15 minutos (slides 5 a 9)
Orientação: Solicitar que em duplas a turma discuta a questão. Cada aluno da dupla pode fazer a rotação de um dos 2 vértices necessários do triângulo.
Propósito: Levar o aluno a pensar como determinar os simétricos de um ponto.
Discuta com a turma:
1) Qual é o primeiro passo para rotacionar o ponto B?
2) Após ligarmos o ponto B ao ponto A, prolongando a reta para servir de suporte para o transferidor, o que devemos fazer?
3) Após marcarmos o ângulo de 90º sobre a reta BA, o que devemos fazer?
4) Após verificarmos, com o compasso, a distância entre os pontos B e A e marcamos essa distância no novo segmento desenhado, podemos proceder da mesma forma para rotacionar o ponto C?
5) Marcados os pontos B’ e C’, basta ligarmos os novos pontos para termos o triângulo rotacionado 60º no entorno do ponto A?
Discussão da solução.
Tempo sugerido: 15 minutos (slides 5 a 9)
Orientação: Solicitar que em duplas a turma discuta a questão. Cada aluno da dupla pode fazer a rotação de um dos 2 vértices necessários do triângulo.
Propósito: Levar o aluno a pensar como determinar os simétricos de um ponto.
Discuta com a turma:
1) Qual é o primeiro passo para rotacionar o ponto B?
2) Após ligarmos o ponto B ao ponto A, prolongando a reta para servir de suporte para o transferidor, o que devemos fazer?
3) Após marcarmos o ângulo de 90º sobre a reta BA, o que devemos fazer?
4) Após verificarmos, com o compasso, a distância entre os pontos B e A e marcamos essa distância no novo segmento desenhado, podemos proceder da mesma forma para rotacionar o ponto C?
5) Marcados os pontos B’ e C’, basta ligarmos os novos pontos para termos o triângulo rotacionado 60º no entorno do ponto A?
Discussão da solução.
Tempo sugerido: 15 minutos (slides 5 a 9)
Orientação: Solicitar que em duplas a turma discuta a questão. Cada aluno da dupla pode fazer a rotação de um dos 2 vértices necessários do triângulo.
Propósito: Levar o aluno a pensar como determinar os simétricos de um ponto.
Discuta com a turma:
1) Qual é o primeiro passo para rotacionar o ponto B?
2) Após ligarmos o ponto B ao ponto A, prolongando a reta para servir de suporte para o transferidor, o que devemos fazer?
3) Após marcarmos o ângulo de 90º sobre a reta BA, o que devemos fazer?
4) Após verificarmos, com o compasso, a distância entre os pontos B e A e marcamos essa distância no novo segmento desenhado, podemos proceder da mesma forma para rotacionar o ponto C?
5) Marcados os pontos B’ e C’, basta ligarmos os novos pontos para termos o triângulo rotacionado 60º no entorno do ponto A?
Sistematização do conceito

Tempo sugerido: 5 minutos
Orientação: Compartilhar com os alunos o conceito que foi trabalhado nesta aula: rotação.
Propósito: Concluir o conceito que foi trabalhado na aula.
Encerramento
Tempo sugerido: 1 minuto
Orientação: Encerrar a aula frisando o procedimento para rotacionar uma imagem.
Propósito: Realizar um fechamento das ideias discutidas.
Raio X
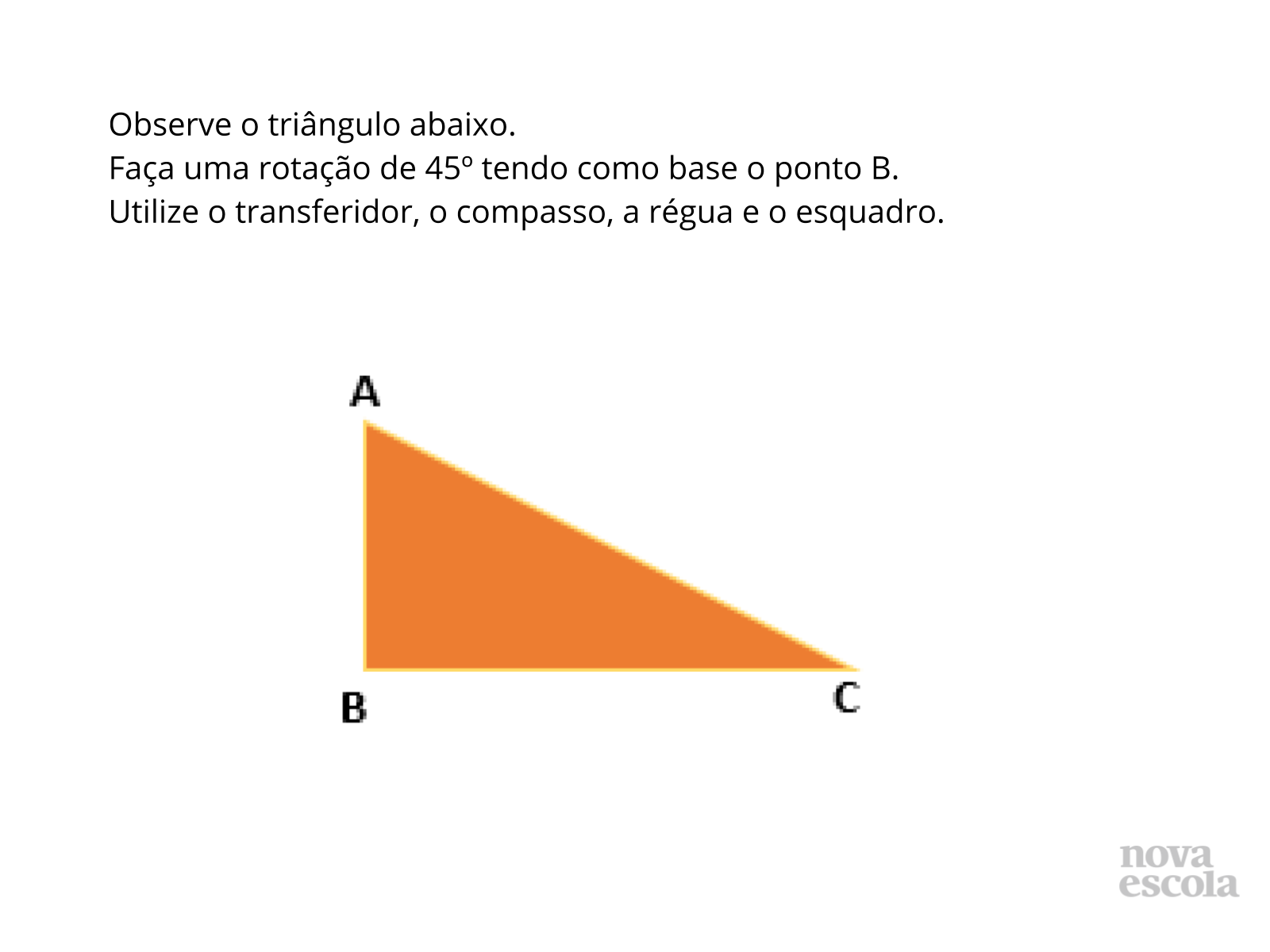
Tempo sugerido: 10 minutos.
Orientações: A atividade deverá ser realizada individualmente. Circule para verificar como os alunos estão realizando a marcação dos pontos. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando a solução na lousa.
Propósito: Verificar se os alunos entenderam o conceito de rotação e sabem aplicá-lo utilizando os instrumentos necessários.