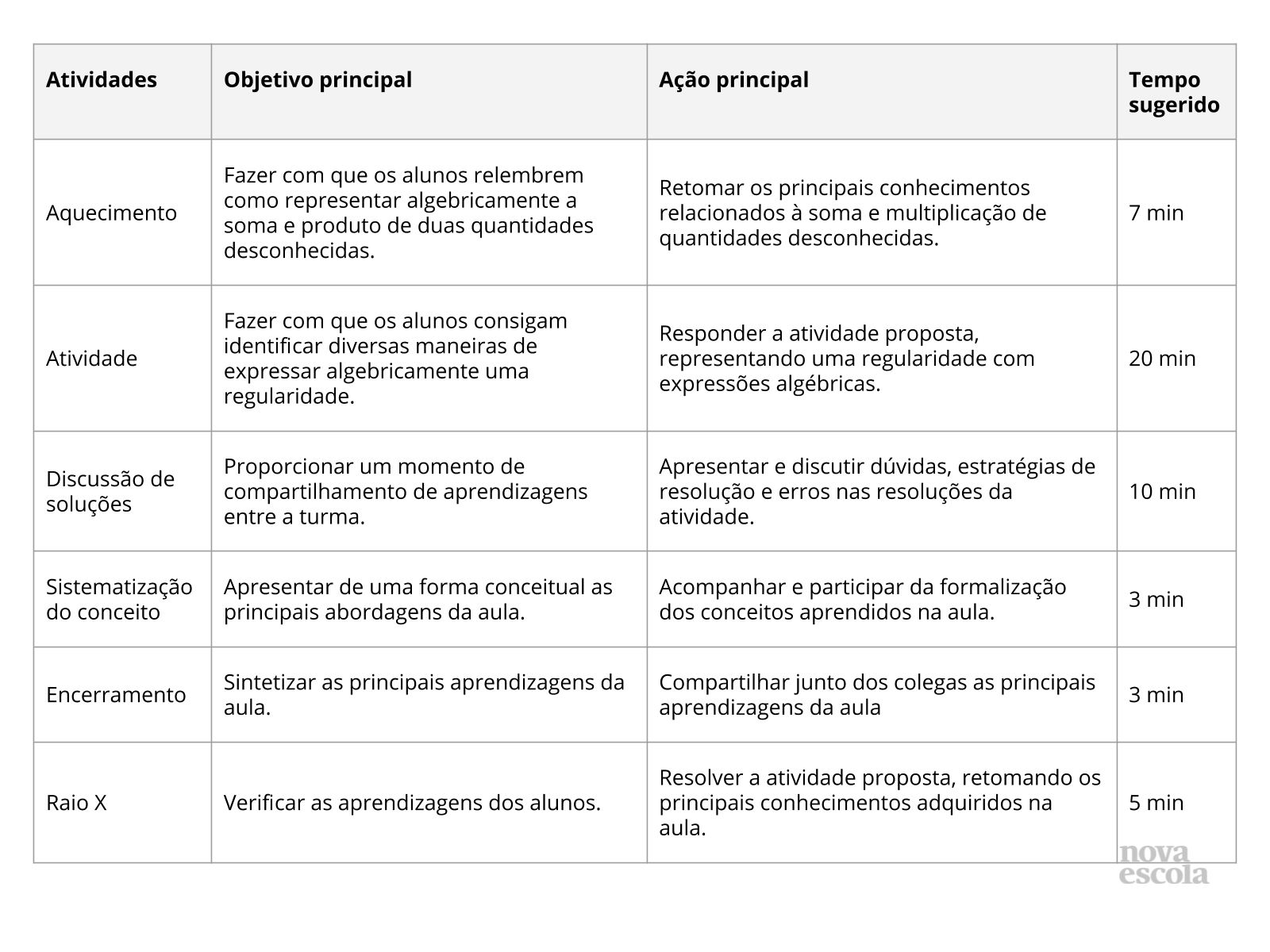
Atividade principal
Plano de Aula
Plano de aula: Representando algebricamente a regularidade de uma sequência
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Regularidades algébricas em uma sequência
Por: Lucas Henrique Viana
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Lucas Henrique Viana
Mentor: Rodrigo Morozetti Blanco
Especialista de área: Sandra Regina Correa Amorim
Habilidade da BNCC
EF07MA12 - Reconhecer se duas expressões algébricas obtidas para descrever a regularidade de uma mesma sequência numérica são ou não equivalentes.
Objetivos específicos
Identificar diversas maneiras de expressar algebricamente uma regularidade.
Conceito-chave
Representação algébrica de regularidades em sequências.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
Habilidades BNCC:
Objetivos de aprendizagem
Identificar diversas maneiras de expressar algebricamente uma regularidade.
Resumo da aula
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete (ou leia) o objetivo para a turma.
Propósito: Compartilhar com os alunos o objetivo da aula.
Aquecimento

Tempo sugerido: 7 minutos (slides 3 a 6)
Orientação: Projete e/ou leia o enunciado da atividade junto dos alunos, certificando-se que todos compreenderam as informações fornecidas. Logo após, proponha uma resolução coletiva de cada questão, revendo o uso da linguagem algébrica na representação de regularidades.
Assim, o total de biscoitos será representado por X + Y e 2X. Já o total de quadradinhos de chocolate será representado por 3X e X².
Propósito: Fazer com que o estudante retome suas conhecimentos sobre expressões algébricas.
Aquecimento

Tempo sugerido: 7 minutos (slides 3 a 6)
Orientação: Projete e/ou leia o enunciado da atividade junto dos alunos, certificando-se que todos compreenderam as informações fornecidas. Logo após, proponha uma resolução coletiva de cada questão, revendo o uso da linguagem algébrica na representação de regularidades.
Assim, o total de biscoitos será representado por X + Y e 2X. Já o total de quadradinhos de chocolate será representado por 3X e X².
Propósito: Fazer com que o estudante retome suas conhecimentos sobre expressões algébricas.
Aquecimento

Tempo sugerido: 7 minutos (slides 3 a 6)
Orientação: Projete e/ou leia o enunciado da atividade junto dos alunos, certificando-se que todos compreenderam as informações fornecidas. Logo após, proponha uma resolução coletiva de cada questão, revendo o uso da linguagem algébrica na representação de regularidades.
Assim, o total de biscoitos será representado por X + Y e 2X. Já o total de quadradinhos de chocolate será representado por 3X e X².
Propósito: Fazer com que o estudante retome suas conhecimentos sobre expressões algébricas.
Aquecimento

Tempo sugerido: 7 minutos (slides 3 a 6)
Orientação: Projete e/ou leia o enunciado da atividade junto dos alunos, certificando-se que todos compreenderam as informações fornecidas. Logo após, proponha uma resolução coletiva de cada questão, revendo o uso da linguagem algébrica na representação de regularidades.
Assim, o total de biscoitos será representado por X + Y e 2X. Já o total de quadradinhos de chocolate será representado por 3X e X².
Propósito: Fazer com que o estudante retome suas conhecimentos sobre expressões algébricas.
Atividade principal
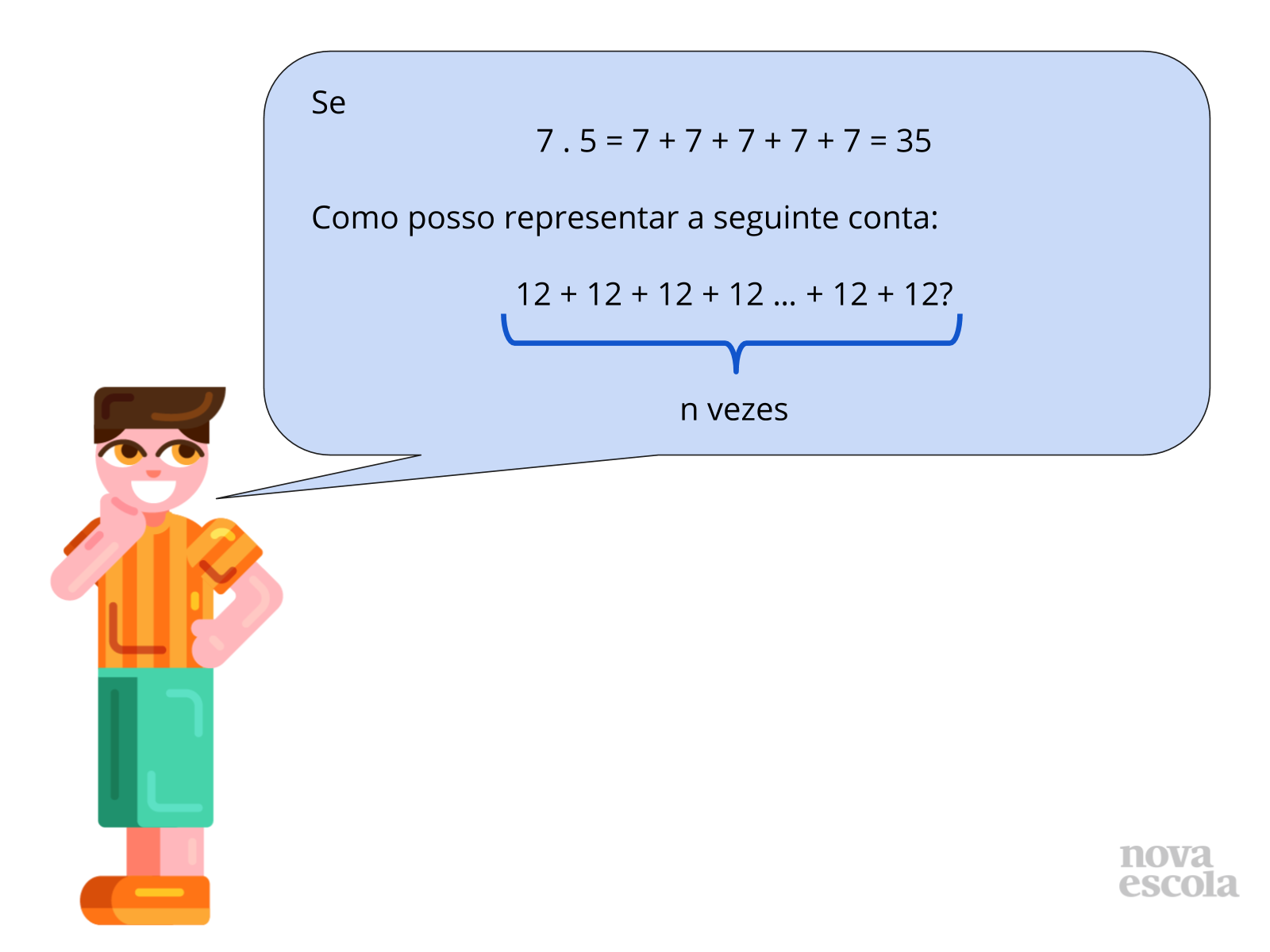
Tempo sugerido: 20 minutos (slides 7 a 11)
Orientação: Sugira que, a princípio, todos os alunos façam a atividade individualmente. Peça para que os estudantes façam uma questão por vez. Na atividade impressa, peça para que façam as questões de 1 a 4, que correspondem aos slides 7 a 10. Após a grande maioria da turma ter respondido, peça para que formem duplas e tentem resolver juntos a questão de número 5, que corresponde ao slide 11.
Ao chegar a essa atividade, certifique-se de que os alunos compreendem que as reticências indicam que que os números são somados ou multiplicados uma quantidade desconhecida de vezes, embora finita. Assim, eles devem usar tal ideia para determinar que essa quantidade desconhecida será a incógnita da expressão.
Enquanto os grupos tentam resolver, circule pela sala e observe as suas estratégias de resolução e se há dúvidas entre os alunos, fazendo as intervenções necessárias (consulte o guia de intervenções para mais detalhes). Nos últimos 5 minutos deste momento, peça para que os as duplas compartilhem entre si as suas resoluções, dúvidas e estratégias.
Propósito: Fazer com que os alunos identifiquem diferentes maneiras de expressar algebricamente uma regularidade.
Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.
Atividade principal
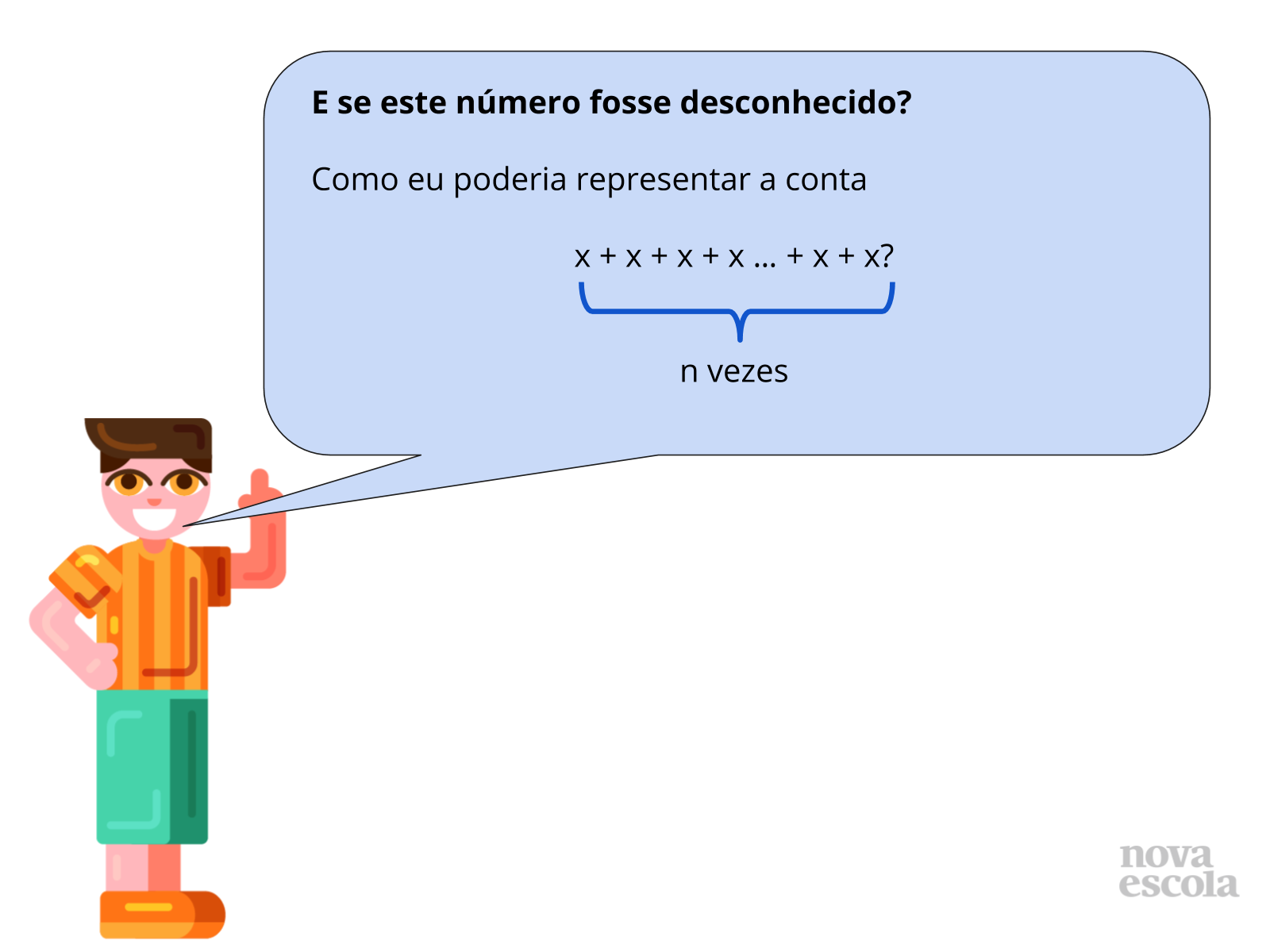
Tempo sugerido: 20 minutos (slides 7 a 11)
Orientação: Sugira que, a princípio, todos os alunos façam a atividade individualmente. Peça para que os estudantes façam uma questão por vez. Na atividade impressa, peça para que façam as questões de 1 a 4, que correspondem aos slides 7 a 10. Após a grande maioria da turma ter respondido, peça para que formem duplas e tentem resolver juntos a questão de número 5, que corresponde ao slide 11.
Ao chegar a essa atividade, certifique-se de que os alunos compreendem que as reticências indicam que que os números são somados ou multiplicados uma quantidade desconhecida de vezes, embora finita. Assim, eles devem usar tal ideia para determinar que essa quantidade desconhecida será a incógnita da expressão.
Enquanto os grupos tentam resolver, circule pela sala e observe as suas estratégias de resolução e se há dúvidas entre os alunos, fazendo as intervenções necessárias (consulte o guia de intervenções para mais detalhes). Nos últimos 5 minutos deste momento, peça para que os as duplas compartilhem entre si as suas resoluções, dúvidas e estratégias.
Propósito: Fazer com que os alunos identifiquem diferentes maneiras de expressar algebricamente uma regularidade.
Atividade principal
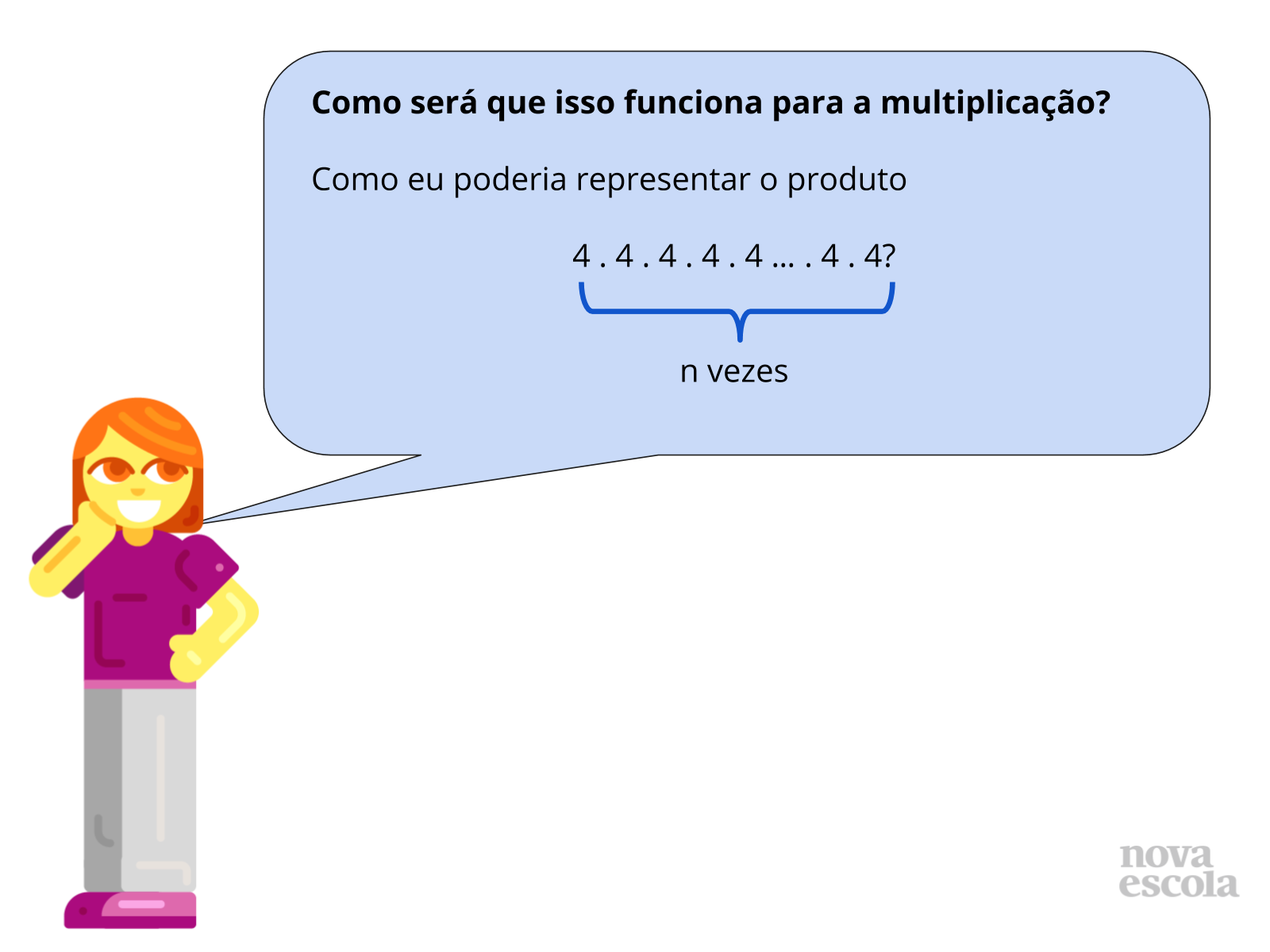
Tempo sugerido: 20 minutos (slides 7 a 11)
Orientação: Sugira que, a princípio, todos os alunos façam a atividade individualmente. Peça para que os estudantes façam uma questão por vez. Na atividade impressa, peça para que façam as questões de 1 a 4, que correspondem aos slides 7 a 10. Após a grande maioria da turma ter respondido, peça para que formem duplas e tentem resolver juntos a questão de número 5, que corresponde ao slide 11.
Ao chegar a essa atividade, certifique-se de que os alunos compreendem que as reticências indicam que que os números são somados ou multiplicados uma quantidade desconhecida de vezes, embora finita. Assim, eles devem usar tal ideia para determinar que essa quantidade desconhecida será a incógnita da expressão.
Enquanto os grupos tentam resolver, circule pela sala e observe as suas estratégias de resolução e se há dúvidas entre os alunos, fazendo as intervenções necessárias (consulte o guia de intervenções para mais detalhes). Nos últimos 5 minutos deste momento, peça para que os as duplas compartilhem entre si as suas resoluções, dúvidas e estratégias.
Propósito: Fazer com que os alunos identifiquem diferentes maneiras de expressar algebricamente uma regularidade.
Atividade principal
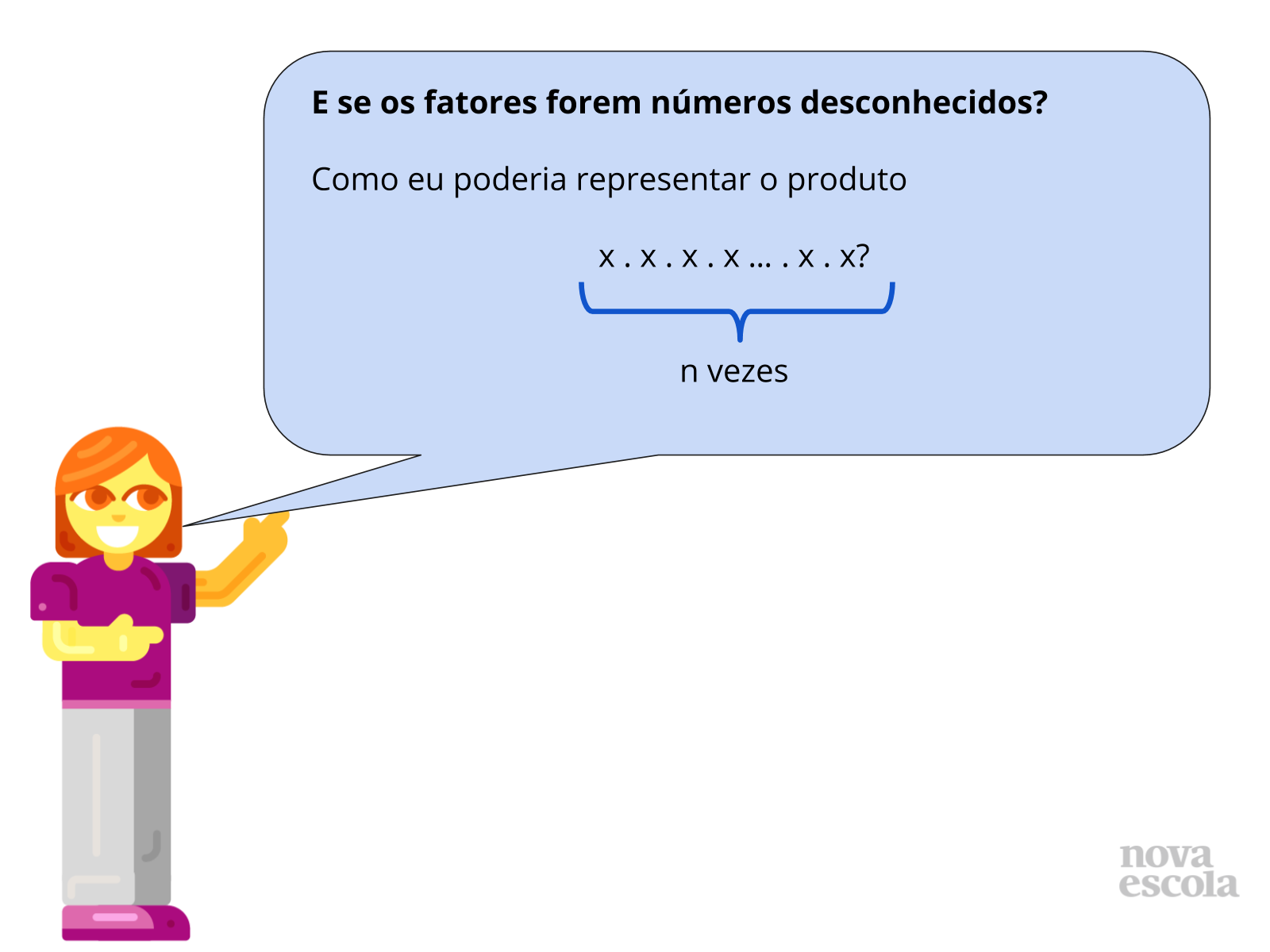
Tempo sugerido: 20 minutos (slides 7 a 11)
Orientação: Sugira que, a princípio, todos os alunos façam a atividade individualmente. Peça para que os estudantes façam uma questão por vez. Na atividade impressa, peça para que façam as questões de 1 a 4, que correspondem aos slides 7 a 10. Após a grande maioria da turma ter respondido, peça para que formem duplas e tentem resolver juntos a questão de número 5, que corresponde ao slide 11.
Ao chegar a essa atividade, certifique-se de que os alunos compreendem que as reticências indicam que que os números são somados ou multiplicados uma quantidade desconhecida de vezes, embora finita. Assim, eles devem usar tal ideia para determinar que essa quantidade desconhecida será a incógnita da expressão.
Enquanto os grupos tentam resolver, circule pela sala e observe as suas estratégias de resolução e se há dúvidas entre os alunos, fazendo as intervenções necessárias (consulte o guia de intervenções para mais detalhes). Nos últimos 5 minutos deste momento, peça para que os as duplas compartilhem entre si as suas resoluções, dúvidas e estratégias.
Propósito: Fazer com que os alunos identifiquem diferentes maneiras de expressar algebricamente uma regularidade.
Atividade principal

Tempo sugerido: 20 minutos (slides 7 a 11)
Orientação: Sugira que, a princípio, todos os alunos façam a atividade individualmente. Peça para que os estudantes façam uma questão por vez. Na atividade impressa, peça para que façam as questões de 1 a 4, que correspondem aos slides 7 a 10. Após a grande maioria da turma ter respondido, peça para que formem duplas e tentem resolver juntos a questão de número 5, que corresponde ao slide 11.
Ao chegar a essa atividade, certifique-se de que os alunos compreendem que as reticências indicam que que os números são somados ou multiplicados uma quantidade desconhecida de vezes, embora finita. Assim, eles devem usar tal ideia para determinar que essa quantidade desconhecida será a incógnita da expressão.
Enquanto os grupos tentam resolver, circule pela sala e observe as suas estratégias de resolução e se há dúvidas entre os alunos, fazendo as intervenções necessárias (consulte o guia de intervenções para mais detalhes). Nos últimos 5 minutos deste momento, peça para que os as duplas compartilhem entre si as suas resoluções, dúvidas e estratégias.
Propósito: Fazer com que os alunos identifiquem diferentes maneiras de expressar algebricamente uma regularidade.
Discussão das soluções
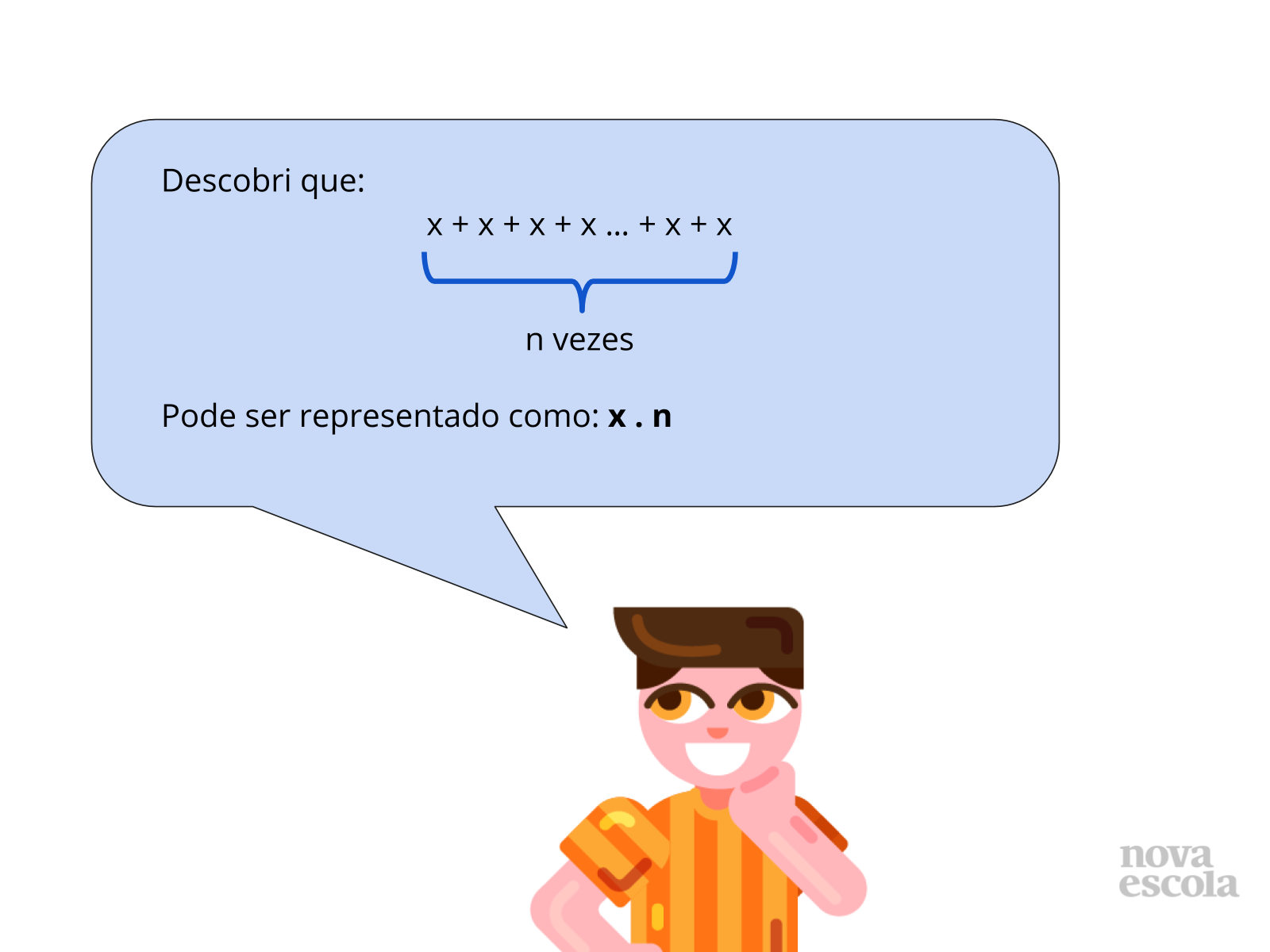
Tempo sugerido: 11 minutos (slides 12 a 14)
Orientação: Solicite que alguns alunos compartilhem suas resoluções na lousa, perguntando sempre se a turma concorda com tal resolução, ou se resolveram de maneiras diferentes, para que todos possam compartilhar suas estratégias, dúvidas e erros.
Caso alguma das estratégias apresentadas possuam erros, discuta com a turma onde aconteceram os erros e como ele poderia ter sido evitado, de modo que todos possam aprender a partir dos erros.
Apresente também as resoluções dos slides 12 a 14, verificando principalmente se os alunos entendem os procedimentos de cálculo utilizados no slide 14.
Propósito: Discutir junto dos alunos as diferentes resoluções encontradas por eles.
Discussão das soluções
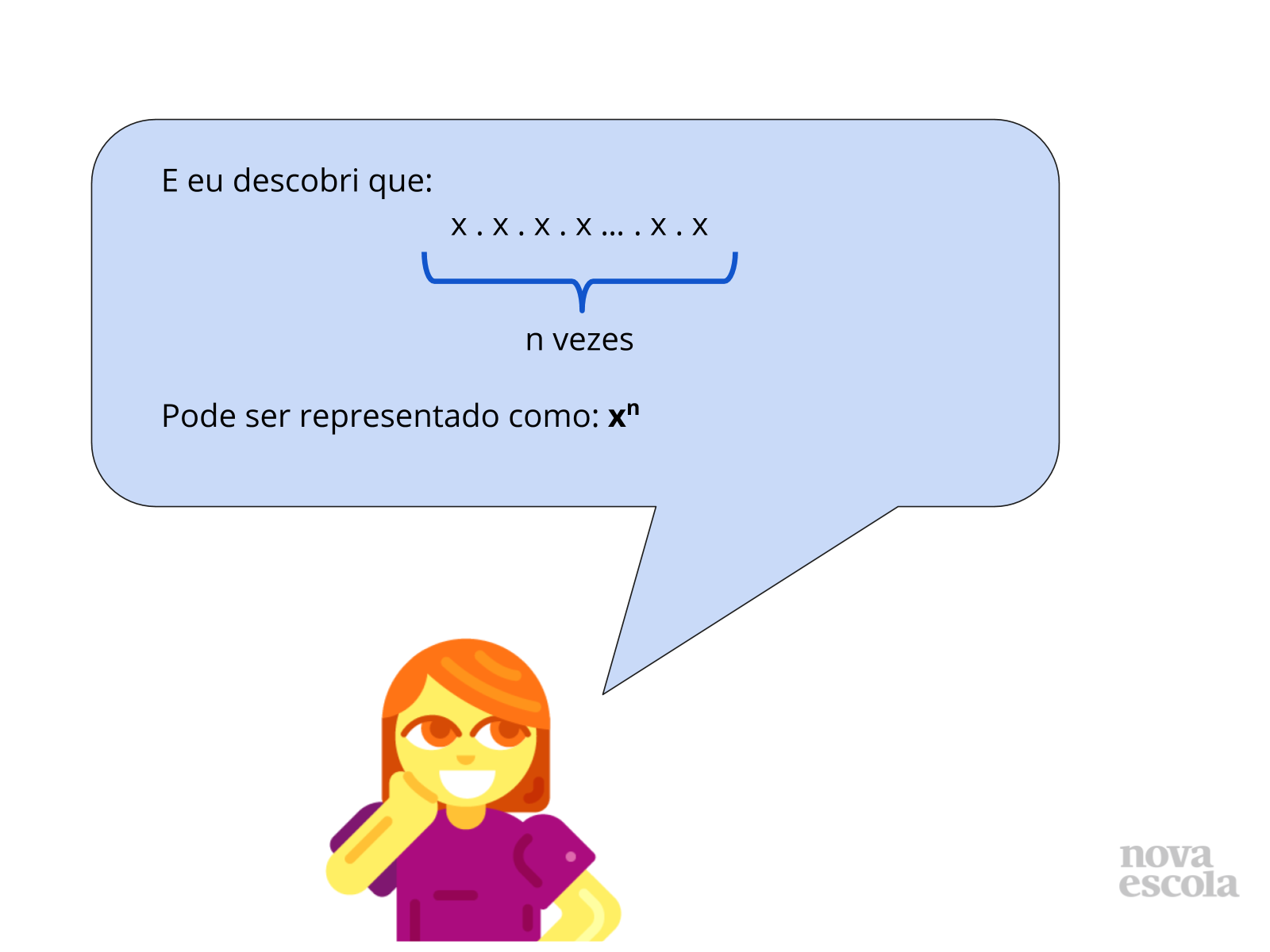
Tempo sugerido: 11 minutos (slides 12 a 14)
Orientação: Solicite que alguns alunos compartilhem suas resoluções na lousa, perguntando sempre se a turma concorda com tal resolução, ou se resolveram de maneiras diferentes, para que todos possam compartilhar suas estratégias, dúvidas e erros.
Caso alguma das estratégias apresentadas possuam erros, discuta com a turma onde aconteceram os erros e como ele poderia ter sido evitado, de modo que todos possam aprender a partir dos erros.
Apresente também as resoluções dos slides 12 a 14, verificando principalmente se os alunos entendem os procedimentos de cálculo utilizados no slide 14.
Propósito: Discutir junto dos alunos as diferentes resoluções encontradas por eles.
Discussão das soluções

Tempo sugerido: 11 minutos (slides 12 a 14)
Orientação: Solicite que alguns alunos compartilhem suas resoluções na lousa, perguntando sempre se a turma concorda com tal resolução, ou se resolveram de maneiras diferentes, para que todos possam compartilhar suas estratégias, dúvidas e erros.
Caso alguma das estratégias apresentadas possuam erros, discuta com a turma onde aconteceram os erros e como ele poderia ter sido evitado, de modo que todos possam aprender a partir dos erros.
Apresente também as resoluções dos slides 12 a 14, verificando principalmente se os alunos entendem os procedimentos de cálculo utilizados no slide 14.
Propósito: Discutir junto dos alunos as diferentes resoluções encontradas por eles.
Sistematização do conceito

Tempo sugerido: 3 minutos
Orientação: Leia atentamente junto dos alunos as informações do slide, destacando especialmente os procedimentos realizados na segunda expressão.
Propósito: Conceituar as principais aprendizagens da aula.
Encerramento

Tempo sugerido: 3 minutos
Orientação: Encerre a atividade retomando com os estudantes as principais aprendizagens da aula.
Propósito: Destacar as principais aprendizagens da aula.
Raio x

Tempo sugerido: 5 minutos
Orientação: Peça para que os alunos respondam individualmente esta atividade. Enquanto respondem, circule pela sala e observe as estratégias de resolução que os alunos utilizam, se ainda há dúvidas ou se alguém não consegue iniciar a atividade. Faça as intervenções que forem necessárias, mas sem impedir que o aluno tente por conta própria encontrar uma resposta. Você pode acessar logo abaixo algumas atividades complementares que poderão contribuir na consolidação da aprendizagem dos alunos.
Propósito: Verificar se os alunos conseguem aplicar os conhecimentos adquiridos durante a aula em uma atividade.
Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT7_12ALG01
Recursos
- caderno
- lápis
- grupo de alunos no Whatsapp
- Opcionais:
- Google Sala de Aula
- Meet
Para este plano, foque na etapa: Atividade Principal
Aquecimento
Essa etapa é um pontapé para o início da aula, a proposta é uma resolução coletiva da atividade pela turma. Se for possível uma aula síncrona usando o Meet ou Zoom, por exemplo, disponibilize o problema proposto e instigue a participação da turma usando boas perguntas, fazendo com que cheguem na resposta correta. Caso não seja possível o uso desta tecnologia, utilize o WhatsApp ou e-mail, para que os alunos pensem e neste caso individualmente sobre o problema proposto.
Atividade principal
Se estiver em uma aula síncrona, apresente logo após a atividade de aquecimento a principal. O intuito é que os alunos pensem e identifiquem diferentes maneiras de expressar algebricamente uma regularidade. Caso não seja possível, compartilhe a atividade pelo meio que a turma escolheu para comunicação.
Discussão das soluções
Compartilhe as resoluções usando um Doc ou Jambord, perguntando sempre se a turma concorda com tal resolução, ou se resolveram de maneiras diferentes, para que todos possam compartilhar suas estratégias, dúvidas e erros. Caso a aula síncrona não seja possível, grave um vídeo ou áudio com a discussão da atividade e disponibilize para a turma.
Sistematização
Conceitue a aprendizagem da aula, compartilhando o slide dessa etapa da aula. Peça que os alunos registrem as informações do slide no caderno.
Raio X
O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto. Compartilhe a imagem do slide com os alunos usando o recurso de email ou foto via whatsapp. Peça que respondam à questão e lhe devolva com ele resolvido. Analise as respostas e elabore devolutivas individuais sobre a atividade e reenvie com comentários para os alunos.
Convite às famílias
Oriente às famílias a auxiliarem na leitura das comandas e no envio das soluções, conforme os combinados com o professor. É importante que as famílias acompanhem as atividades nos canais de comunicação estabelecidos entre a escola, professor e família.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Lucas Henrique Viana
Mentor: Rodrigo Morozetti Blanco
Especialista de área: Sandra Regina Correa Amorim
Habilidade da BNCC
EF07MA12 - Reconhecer se duas expressões algébricas obtidas para descrever a regularidade de uma mesma sequência numérica são ou não equivalentes.
Objetivos específicos
Identificar diversas maneiras de expressar algebricamente uma regularidade.
Conceito-chave
Representação algébrica de regularidades em sequências.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.










