Resumo da aula
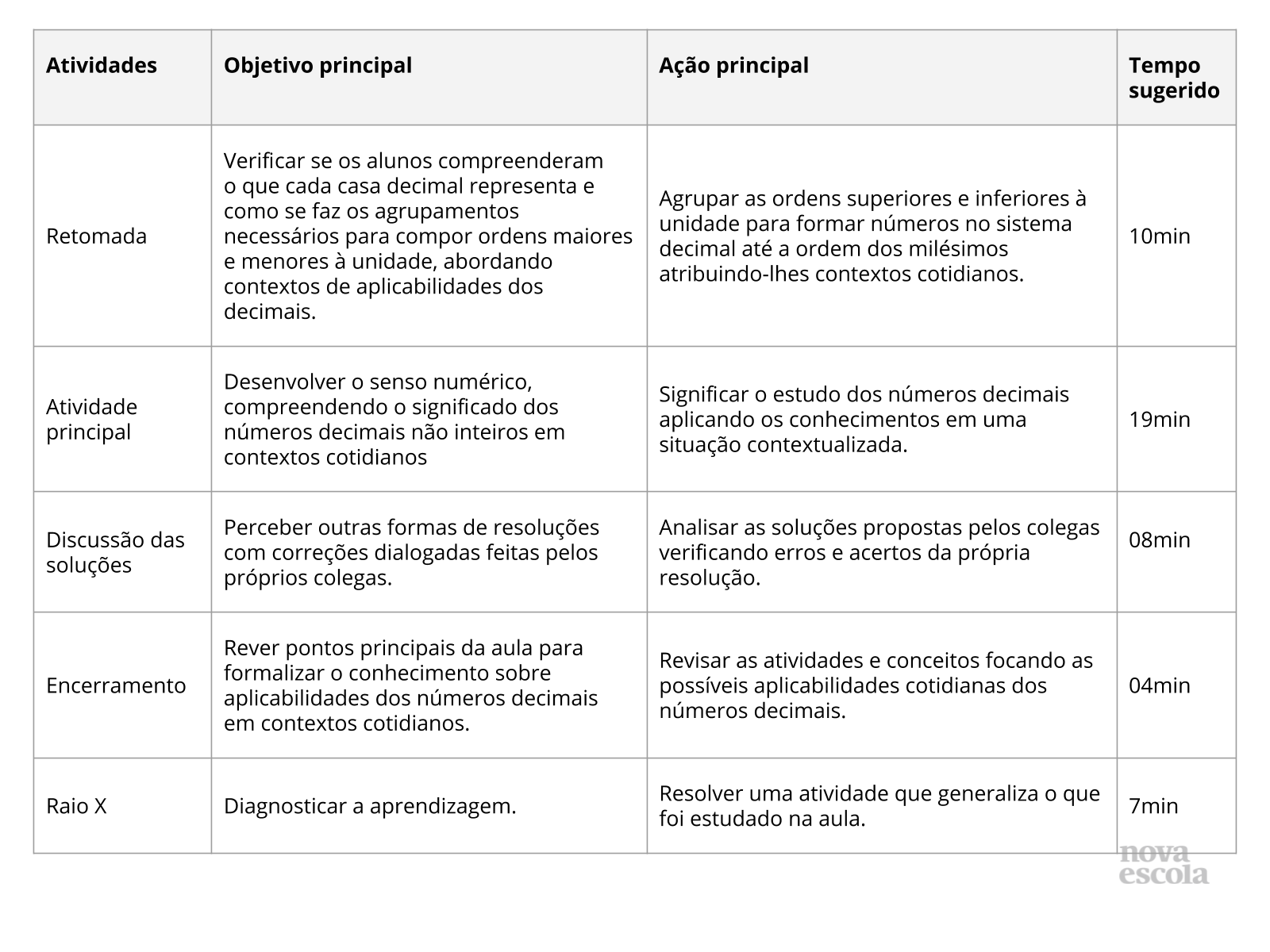
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 10 minutos (Slides 3 e 4)
Orientação: Professor, leia para seus alunos, ou peça para um aluno ler a fala do personagem desse slide e o exemplo do slide seguinte. Convide os alunos a irem até o quadro para preencher a tabela, assim você pode acompanhar os raciocínios deles e junto com todos os alunos trocar ideias sobre outras possibilidades de preenchimentos.
Propósito: Retomar conhecimentos já estudados.
Discuta com a turma:
- Vocês entenderam o que é para fazer?
- Alguém consegue nos explicar o que é para fazer?
- Alguém pode nos apresentar um exemplo de quando é possível fazermos o arredondamento de um número?
- Alguém pode nos dar mais alguma ideia para o que esse número pode representar?
- Onde vocês já viram números parecidos com esses?
- Para fazer possíveis arredondamentos, o que é necessário levarmos em conta?
Retomada
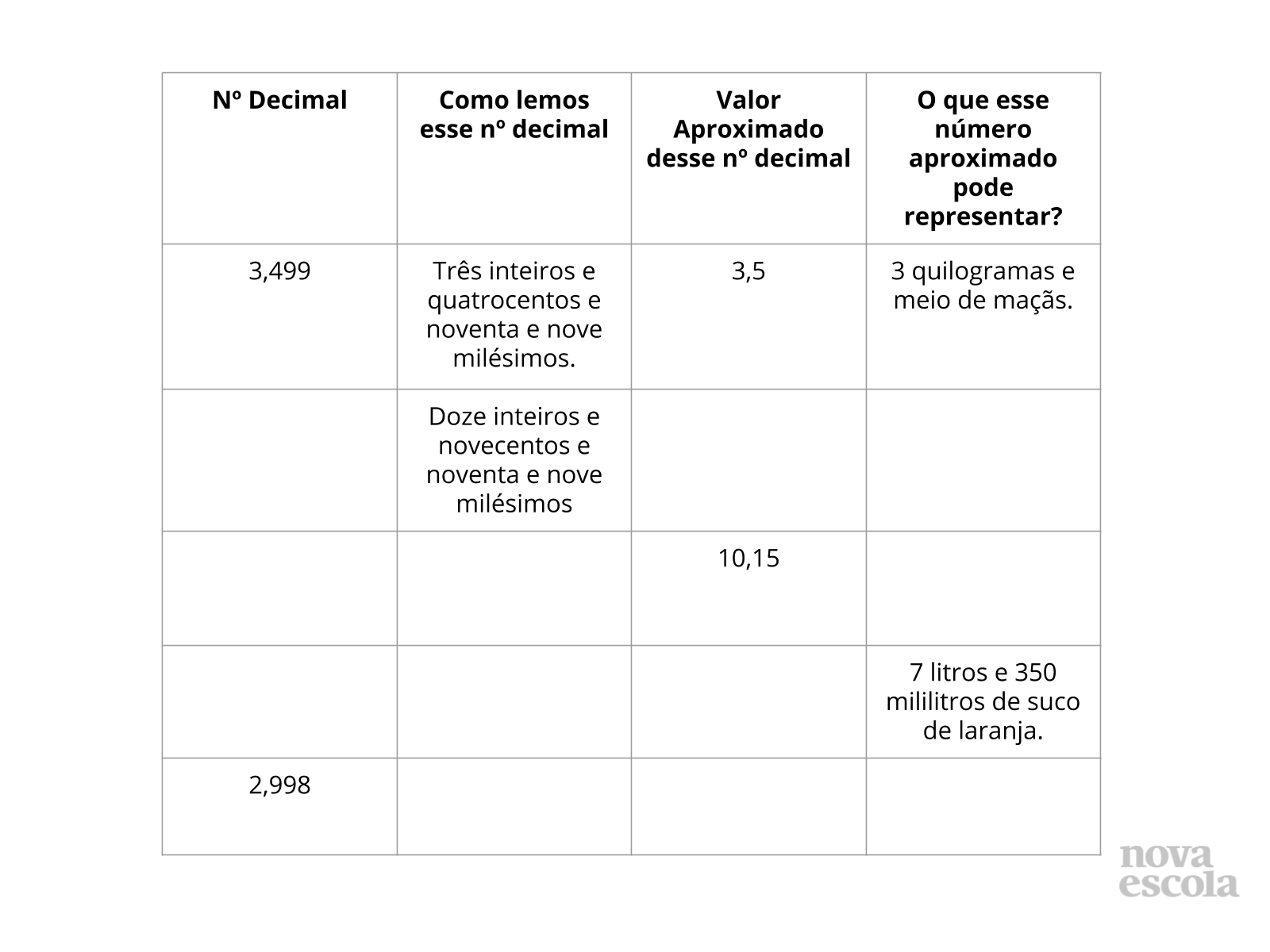
Tempo sugerido: 10 minutos (Slides 3 e 4)
Orientação: Professor leia para seus alunos, ou peça para um aluno ler a fala do personagem desse slide e o exemplo do slide seguinte. Convide os alunos a irem até o quadro para preencher a tabela, assim você pode acompanhar os raciocínios deles e junto com todos os alunos trocar ideias sobre outras possibilidades de preenchimentos.
Propósito: Retomar conhecimentos já estudados.
Discuta com a turma:
- Vocês entenderam o que é para fazer?
- Alguém consegue nos explicar o que é para fazer?
- Alguém pode nos apresentar um exemplo de quando é possível fazermos o arredondamento de um número?
- Alguém pode nos dar mais alguma ideia para o que esse número pode representar?
- Onde vocês já viram números parecidos com esses?
- Para fazer possíveis arredondamentos, o que é necessário levarmos em conta?
Atividade Principal

Tempo sugerido: 19 minutos
Orientação: Professor, incentive seus alunos a resolver o exercício sozinhos. Solicite que eles pesquisem em seus livros didáticos sobre as relações entre os valores de medidas de capacidade, ou leve algumas tabelas com os valores de medidas de capacidade e entregue para eles usarem como referência. Oriente-os a imaginarem a situação para propor sua resolução e registrarem em seus cadernos como pensaram para chegar no resultado. Sempre que achar necessário, solicite que expliquem verbalmente seus pensamentos e anotações.
Propósito: Levar os alunos a perceberem diferentes contextos de aplicabilidade dos números decimais, significando a aprendizagem.
Discuta com a turma:
- vocês fazem suco na casa de vocês?
- como vocês medem as quantidades de líquidos na sua casa? Vocês usam copo medidor?
- Quantos copinhos de 10 ml vocês consegue encher com uma jarra de 1 litro?
- Onde mais podemos encontrar números decimais que representam quantidades em mililitros?
- E em gramas? Em quilogramas? Em litros?
Discussão da Solução
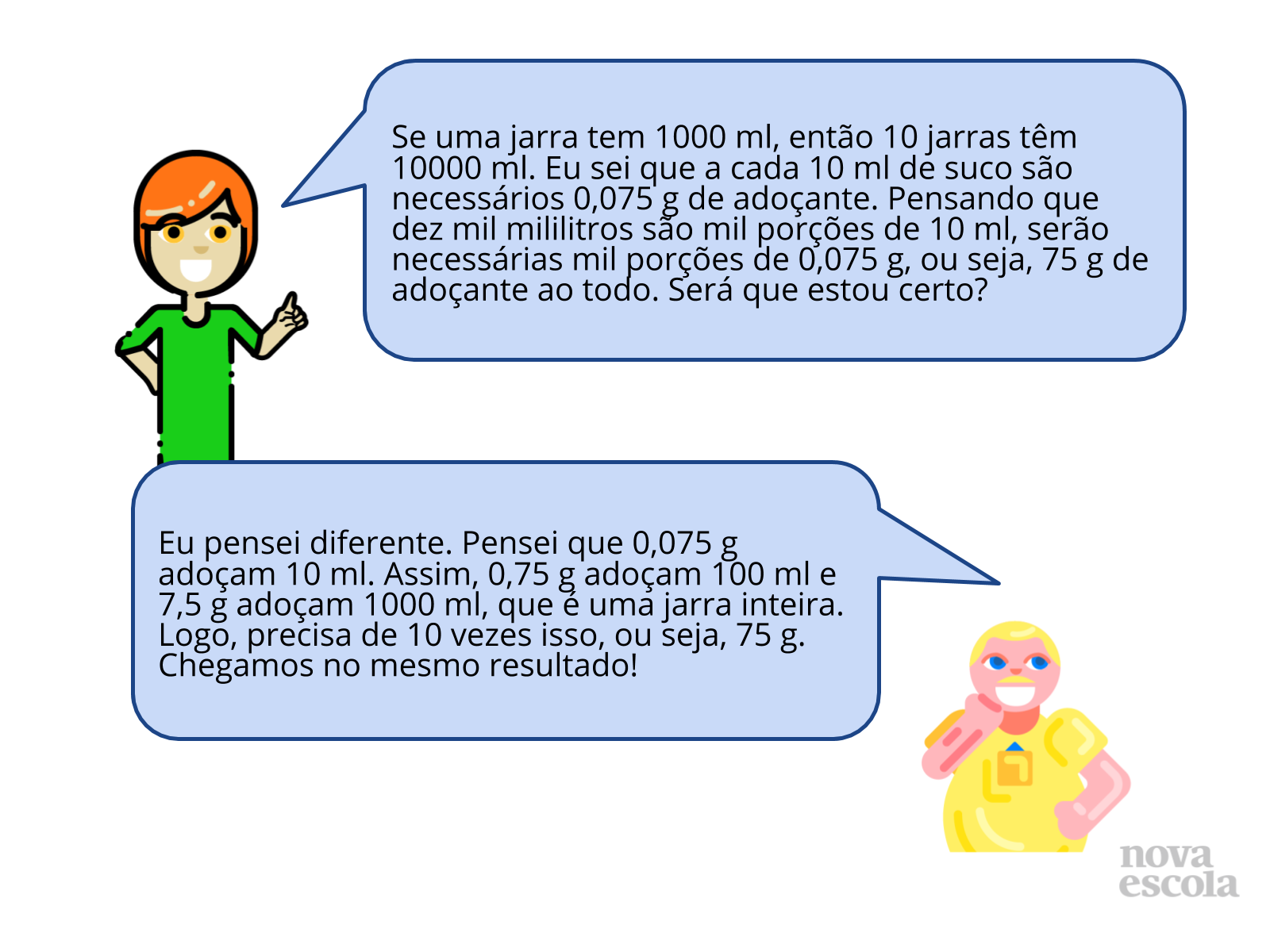
Tempo sugerido: 8 minutos
Orientação: Professor, leve os alunos a analisarem as soluções propostas no slide e também outras soluções propostas pelos colegas, verificando erros, acertos e novas possibilidades resolutivas.
Propósito: verificar a possibilidade de resolver a atividade por caminhos matemáticos diferentes, mas adequados à resolução e ao estudo dos números decimais.
Discuta com a turma:
- O que vocês acharam da primeira resolução apresentada no slide? E da segunda? Qual delas você acha melhor? Por quê?
- Alguém tem uma ideia diferente de resolução? Você poderia explicar ela para nós?
- Em que pontos você acha que sua ideia de resolução é melhor do que as apresentadas no slides?
Encerramento

Tempo sugerido: 4 minutos
Orientação: Professor procure destacar várias situações onde são aplicados, ou aparecem os números decimais. Se achar pertinente, você pode pedir aos alunos para criarem exemplos de aplicabilidades de números decimais em situações cotidianas e depois oriente-os a compor unidades usando números decimais dentro dos exemplos que eles mesmos criaram.
Propósito: Concluir a aprendizagem objetivada para esta aula, percebendo que diferentes contextos onde aparecem e onde usamos os números decimais e suas composições.
Discuta com a turma:
- Você consegue relatar o que mais você aprendeu na aula de hoje, apresentando exemplos de onde aparecem os números decimais em situações da sua vida e nos explicar como você pode trabalhar com esses números?
Raio X

Tempo sugerido: 7 minutos
Orientação: Professor entregue uma atividade Raio X para cada aluno e deixe-os resolver sozinhos. Ao final, recolha a atividade para que seja possível avaliar o nível de aprendizagem da turma.
Propósito: Resolver uma atividade que generaliza o que foi estudado na aula para diagnosticar a aprendizagem.


















