Atividade principal
Plano de Aula
Plano de aula: Ideias e a operação inversa da divisão para estimar um quociente
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Estimativa de quocientes
Por: Isabel Cossalter
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Isabel Cossalter
Mentor: Elisa Greenhalgh Vilalta
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA04 - Utilizar as relações entre adição e subtração, bem como entre multiplicação e divisão, para ampliar as estratégias de cálculo.
Objetivos específicos
Rever as ideias da divisão e do uso da multiplicação como operação inversa para estimar um quociente.
Conceito-chave
Estimativa de um quociente.
Recursos necessários
- Folha de papel A4 branca.
- Cartelas a serem trabalhadas no bingo.
- Atividades impressas em folhas, coladas no caderno ou não.
- Lápis e borracha.
Habilidades BNCC:
Objetivos de aprendizagem
Rever as ideias da divisão e do uso da multiplicação como operação inversa para estimar um quociente.
Resumo da aula
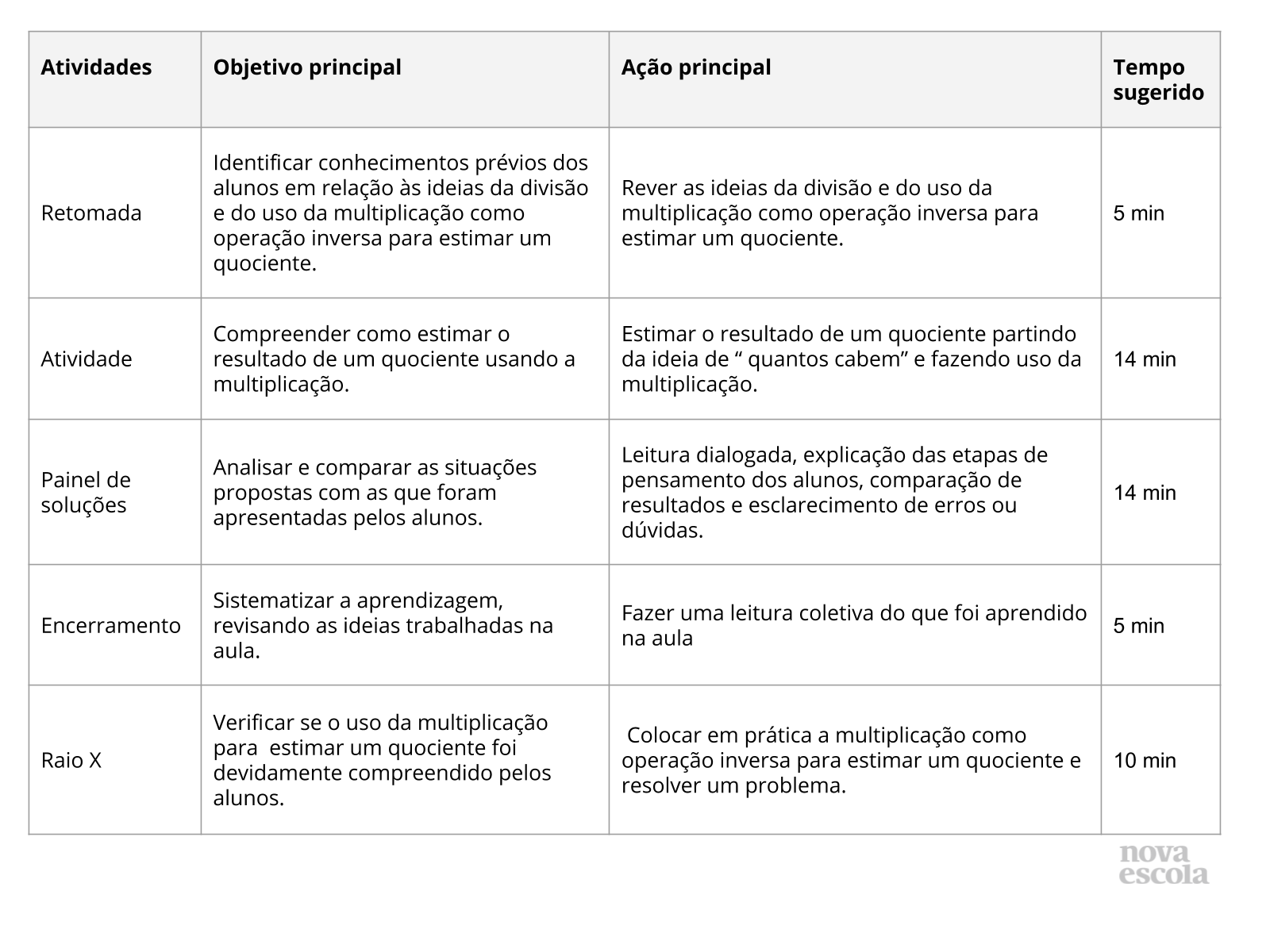 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Propósito: Apresentar aos alunos o objetivo da aula.
Orientação: Leia com as crianças ou peça a um aluno que leia o objetivo em voz alta.
Discuta com a turma:
- Vocês já sabem o que é estimar um quociente, certo? Alguém ainda tem dúvida? Todos se lembram o que é um quociente?
- O objetivo começa assim: “relembrar as ideias e a operação inversa da divisão”. O que é uma operação inversa? Qual é a operação inversa da divisão? Quem se lembra alguma das ideias da divisão?
Retomada

Tempo sugerido: 5 minutos (slides 3 a 5)
Propósito: Rever as ideias da divisão e do uso da multiplicação como operação inversa para estimar um quociente.
Orientação: Leia com a classe ou peça que um ou dois alunos leiam o problema e a fala do garoto. Pergunte às crianças o que acharam da opinião do Bruno e se alguém discordar peça que justifique matematicamente. Em seguida,leia a explicação de Karina e verifique se todos compreenderam o raciocínio da menina. Passe para o questionamento feito por ela e volte a atenção da turma para o problema que vem a seguir. Deixe que discutam brevemente e levantem hipóteses sobre qual ideia da divisão o problema apresenta e de que maneira poderiam resolvê-lo. Finalize a retomada apresentando a fala de Mariana.
Discuta com a turma:
- Como podemos perceber qual é a ideia da divisão presente em um problema?
- Compreender as ideias da divisão pode nos ajudar na hora de estimar um quociente? Por quê?
- Qual das duas ideias da divisão apresentadas pode facilitar a estimativa de um quociente?
- Qual é a operação inversa da divisão? Por que a multiplicação é chamada de operação inversa da divisão?
Retomada

Tempo sugerido: 5 minutos (slides 3 a 5)
Propósito: Rever as ideias da divisão e do uso da multiplicação como operação inversa para estimar um quociente.
Orientação: Leia com a classe ou peça que um ou dois alunos leiam o problema e a fala do garoto. Pergunte às crianças o que acharam da opinião do Bruno e se alguém discordar peça que justifique matematicamente. Em seguida,leia a explicação de Karina e verifique se todos compreenderam o raciocínio da menina. Passe para o questionamento feito por ela e volte a atenção da turma para o problema que vem a seguir. Deixe que discutam brevemente e levantem hipóteses sobre qual ideia da divisão o problema apresenta e de que maneira poderiam resolvê-lo. Finalize a retomada apresentando a fala de Mariana.
Discuta com a turma:
- Como podemos perceber qual é a ideia da divisão presente em um problema?
- Compreender as ideias da divisão pode nos ajudar na hora de estimar um quociente? Por quê?
- Qual das duas ideias da divisão apresentadas pode facilitar a estimativa de um quociente?
- Qual é a operação inversa da divisão? Por que a multiplicação é chamada de operação inversa da divisão?
Retomada

Tempo sugerido: 5 minutos (slides 3 a 5)
Propósito: Rever as ideias da divisão e do uso da multiplicação como operação inversa para estimar um quociente.
Orientação: Leia com a classe ou peça que um ou dois alunos leiam o problema e a fala do garoto. Pergunte às crianças o que acharam da opinião do Bruno e se alguém discordar peça que justifique matematicamente. Em seguida,leia a explicação de Karina e verifique se todos compreenderam o raciocínio da menina. Passe para o questionamento feito por ela e volte a atenção da turma para o problema que vem a seguir. Deixe que discutam brevemente e levantem hipóteses sobre qual ideia da divisão o problema apresenta e de que maneira poderiam resolvê-lo.Finalize a retomada apresentando a fala de Mariana.
Discuta com a turma:
- Como podemos perceber qual é a ideia da divisão presente em um problema?
- Compreender as ideias da divisão pode nos ajudar na hora de estimar um quociente? Por quê?
- Qual das duas ideias da divisão apresentadas pode facilitar a estimativa de um quociente?
- Qual é a operação inversa da divisão?
- Por que a multiplicação é chamada de operação inversa da divisão?
Atividade principal

Tempo sugerido: 14 minutos (slides 6 a 8)
Propósito: Compreender como estimar o resultado de um quociente fazendo uso da multiplicação.
Orientação: Leia as regras do jogo com os alunos no slide projetado ou imprima as regras para os alunos lerem. Em seguida, organize as duplas e peça que escolham rapidamente um nome pelo qual serão identificadas. Registre os nomes escolhidos na lousa, assim ficará mais fácil marcar os pontos feitos durante a atividade. Escreva também na lousa a operação sorteada, marque o tempo e deixe que as crianças a encontrem e resolvam na cartela. Quando uma dupla levantar a mão e gritar o nome, dê o tempo por encerrado. Faça a correção na lousa. Dependendo do desempenho do grupo, pode-se corrigir coletivamente todos os cálculos ou apenas aqueles em que crianças apresentarem dificuldade.Lembre-se de registrar a pontuação dos grupos antes de sortear uma nova operação.
A cartela de 12 cálculos deve ser igual para todos os grupos, apenas com a ordem dos cálculos diferente. Dessa forma fica mais fácil apontar erros, acertos e dicas durante a discussão das soluções. Sugestão: alguns dias antes, como forma de preparação para esse jogo, seria interessante propor atividades que trabalhem a memorização das tabuadas (por exemplo, brincadeiras de final de aula ou lições de casa).
Discuta com a turma:
- Realizar a operação de multiplicação facilita o cálculo da estimativa de um quociente?
- Pensar a divisão a partir da ideia de “ quantos cabem” torna mais fácil encontrar uma forma de calcular o quociente? Como?
- O que pode ajudar a tornar mais eficiente o cálculo da estimativa do quociente?
- Saber as tabuadas ajuda a tornar mais rápido o cálculo da estimativa do quociente?
- Vocês tiveram dificuldades? Quais foram? O que fizeram para tentar superá-las?
Material complementar para o professor
- Leia a matéria “ O que é preciso saber para aprender divisão”, sobre o ensino da divisão, aqui:
http://mathema.com.br/reflexoes/o-que-e-preciso-saber-para-fazer-uma-divisao-2/
- Leia a matéria “ Conceito de divisão por meio da ideia do quanto cabe e a relação entre divisão e multiplicação, de 2013, aqui:
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=52299
Atividade principal

Tempo sugerido: 14 minutos (slides 6 a 8)
Propósito: Compreender como estimar o resultado de um quociente fazendo uso da multiplicação.
Orientação: Leia as regras do jogo com os alunos no slide projetado ou imprima as regras para os alunos lerem . Em seguida, organize as duplas e peça que escolham rapidamente um nome pelo qual serão identificadas. Registre os nomes escolhidos na lousa, assim ficará mais fácil marcar os pontos feitos durante a atividade. Escreva também na lousa a operação sorteada, marque o tempo e deixe que as crianças a encontrem e resolvam na cartela. Quando uma dupla levantar a mão e gritar o nome, dê o tempo por encerrado. Faça a correção na lousa. Dependendo do desempenho do grupo, pode-se corrigir coletivamente todos os cálculos ou apenas aqueles em que crianças apresentarem dificuldade. Lembre-se de registrar a pontuação dos grupos antes de sortear uma nova operação. A cartela de 12 cálculos deve ser igual para todos os grupos, dessa forma fica mais fácil apontar erros, acertos e dicas durante a discussão das soluções.
Sugestão: alguns dias antes, como forma de preparação para esse jogo, seria interessante propor atividades que trabalhem a memorização das tabuadas (por exemplo, brincadeiras de final de aula ou lições de casa).
Discuta com a turma:
- Realizar a operação de multiplicação facilita o cálculo da estimativa de um quociente?
- Pensar a divisão a partir da ideia de “ quantos cabem” torna mais fácil encontrar uma forma de calcular o quociente? Como?
- O que pode ajudar a tornar mais eficiente o cálculo da estimativa do quociente?
- Saber as tabuadas ajuda a tornar mais rápido o cálculo da estimativa do quociente?
- Vocês tiveram dificuldades? Quais foram? O que fizeram para tentar superá-las?
Atividade principal

Tempo sugerido: 14 minutos (slides 6 a 8)
Propósito: Compreender como estimar o resultado de um quociente fazendo uso da multiplicação.
Orientação: Leia as regras do jogo com os alunos no slide projetado ou imprima as regras para os alunos lerem (cópia das regras). Em seguida, organize as duplas e peça que escolham rapidamente um nome pelo qual serão identificadas. Registre os nomes escolhidos na lousa, assim ficará mais fácil marcar os pontos feitos durante a atividade. Escreva também na lousa a operação sorteada, marque o tempo e deixe que as crianças a encontrem e resolvam na cartela. Quando uma dupla levantar a mão e gritar o nome, dê o tempo por encerrado. Faça a correção na lousa. Dependendo do desempenho do grupo, pode-se corrigir coletivamente todos os cálculos ou apenas aqueles em que crianças apresentarem dificuldade. Lembre-se de registrar a pontuação dos grupos antes de sortear uma nova operação.
A cartela de 12 cálculos deve ser igual para todos os grupos, apenas com a ordem dos cálculos diferente. Dessa forma fica mais fácil apontar erros, acertos e dicas durante a discussão das soluções. Sugestão: alguns dias antes, como forma de preparação para esse jogo, seria interessante propor atividades que trabalhem a memorização das tabuadas (por exemplo,brincadei ras de final de aula ou lições de casa).
Discuta com a turma:
- Realizar a operação de multiplicação facilita o cálculo da estimativa de um quociente?
- Pensar a divisão a partir da ideia de “quantos cabem” torna mais fácil encontrar uma forma de calcular o quociente? Como?
- O que pode ajudar a tornar mais eficiente o cálculo da estimativa do quociente?
- Saber as tabuadas ajuda a tornar mais rápido o cálculo da estimativa do quociente?
- Vocês tiveram dificuldades? Quais foram? O que fizeram para tentar superá-las?
Discussão da solução

Tempo sugerido: 14 minutos
Propósito: Analisar e comparar as estratégias de cálculo apresentadas pelos alunos para estimar um quociente.
Orientação: Peça a um aluno que leia a fala da garota. Pergunte para as crianças: o raciocínio apresentado pela menina é fácil? Alguém mais pensou como ela? Quais outras formas de calcular usando a multiplicação vocês aplicaram para estimar o quociente?
Conforme for socializando as estratégias, se considerar oportuno, registre algumas dicas apresentadas pelas duplas que possam servir de consulta para a turma em outras atividades que envolvam o cálculo da estimativa de um quociente.
Discuta com a turma:
- Qual ideia da divisão nós usamos para jogar o bingo?
- É possível variar as estratégias de cálculo de um quociente fazendo uso da multiplicação?
- Durante a discussão das soluções, você percebeu alguma dica que possa ser usada para facilitar o cálculo de um quociente?
- Estimar o valor de um quociente quando as tabuadas estão memorizadas é mais rápido? Por quê?
- Por que é importante saber fazer estimativas de um quociente?
Encerramento

Tempo sugerido: 5 minutos
Propósito: Sistematizar a aprendizagem, revisando as ideias trabalhadas na aula.
Orientação: Faça uma leitura compartilhada do slide com os alunos.
Discuta com a turma:
- Do que aprendemos hoje, o que acharam mais interessante?
- Qual estratégia você utilizou para resolver os cálculos? Ela funcionou?
- Se ela não funcionou, no que ela falhou? Como você poderia ter feito para que ela funcionasse?
- Quais dicas podemos dar aos colegas para realizar o cálculo por estimativa de um quociente?
Raio X

Tempo sugerido: 10 minutos
Propósito: Verificar o aprendizado do cálculo por estimativa de um quociente usando a multiplicação.
Orientação: Leia com a turma ou peça que um aluno leia em voz alta o problema. Certifique-se de que todas as crianças compreenderam corretamente o que deve ser feito.
Retome os procedimentos trabalhados na atividade principal e peça que os utilizem para resolver o problema individualmente. Circule pela sala e observe se as crianças estão conseguindo realizar a operação de acordo com o que foi proposto.
Discuta com a turma:
- Como você acha que se saiu ao fazer a estimativa de um cálculo de divisão usando a multiplicação?
- O uso da operação inversa facilita o cálculo da estimativa do quociente? Por quê?
- Você teve dificuldades para realizar a atividade? Quais foram? O que você precisa fazer para superá-las?
- É possível estimar o quociente usando a operação inversa sem saber as tabuadas? Como? Calcular dessa maneira facilita o trabalho?
Possibilidades de resolução:
- 256 : 8 = 32
8 x 32 = 256
Usando a multiplicação por 10 e por 2
8 x 10 = 80
8 x 20 = 160
8 x 30 = 240
8 x 2 = 16
30 + 2 = 32
b) Agrupando pela adição
256 : 8 =
8 + 8 = 16 = 2 pacotes
16 + 16 = 32 = 4 pacotes
32 + 32 = 64 = 8 pacotes
64 + 64 = 128 = 16 pacotes
128 + 128 = 256 = 32 pacotes
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_07NUM_02
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: -
- Opcionais: FlipGrid, Google Meet, Jamboard
Para este plano, foque na etapa Atividade Principal.
Retomada
O professor pode colocar os dois problemas para que os alunos resolvam e pedir que eles identifiquem as semelhanças e as diferenças entre as situações propostas, sempre com as questões propostas para que eles pensem sobre isso. Pedir que identifiquem também qual a operação inversa da divisão e como ela ajuda nos cálculos de dividir. Feito isso, o professor pode mostrar as duas ideias distintas da divisão presentes aqui. Isso pode ser feito usando o FlipGrip para que os alunos expliquem as semelhanças e diferenças, ou por registro escrito.
Atividade principal
O professor pode colocar a cartela do Bingo no Jamboard, com uma tela para cada aluno, e jogar com os alunos de maneira síncrona usando o Google Meet, mas individualmente, não em duplas como proposto para a aula. Caso não seja possível o recurso digital, o professor pode explicar as regras e pedir que os alunos criem novas cartelas e indiquem dicas para os colegas se darem bem no jogo.
Discussão das soluções
Explorar as ideias da divisão com situações hipotéticas do bingo indicado na Atividade Principal, ou ainda com situações problemas que resgatem estes conceitos já estudados pela turma. Isso pode ser feito de maneira síncrona via Google Meet, por registro escrito ou ainda com a apresentação de outros exemplos de situações pelo Google Apresentações.
Sistematização
Não há.
Encerramento
Solicitar que os alunos registrem no caderno o que aprenderam com as atividades em questão.
Raio X
Propor o problema, pedir que resolvam, e depois fazer as questões presentes nas orientações ao professor, seja no registro escrito ou via Google Formulários.
Importante que após a realização da atividade, a turma tenha acesso às diferentes resoluções para a mesma operação conforme indicado nas orientações.
Convite às famílias
Convidar a família a jogar com o aluno o Bingo indicado na Atividade Principal, proporcionando uma importante interação para o âmbito familiar.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Isabel Cossalter
Mentor: Elisa Greenhalgh Vilalta
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA04 - Utilizar as relações entre adição e subtração, bem como entre multiplicação e divisão, para ampliar as estratégias de cálculo.
Objetivos específicos
Rever as ideias da divisão e do uso da multiplicação como operação inversa para estimar um quociente.
Conceito-chave
Estimativa de um quociente.
Recursos necessários
- Folha de papel A4 branca.
- Cartelas a serem trabalhadas no bingo.
- Atividades impressas em folhas, coladas no caderno ou não.
- Lápis e borracha.









