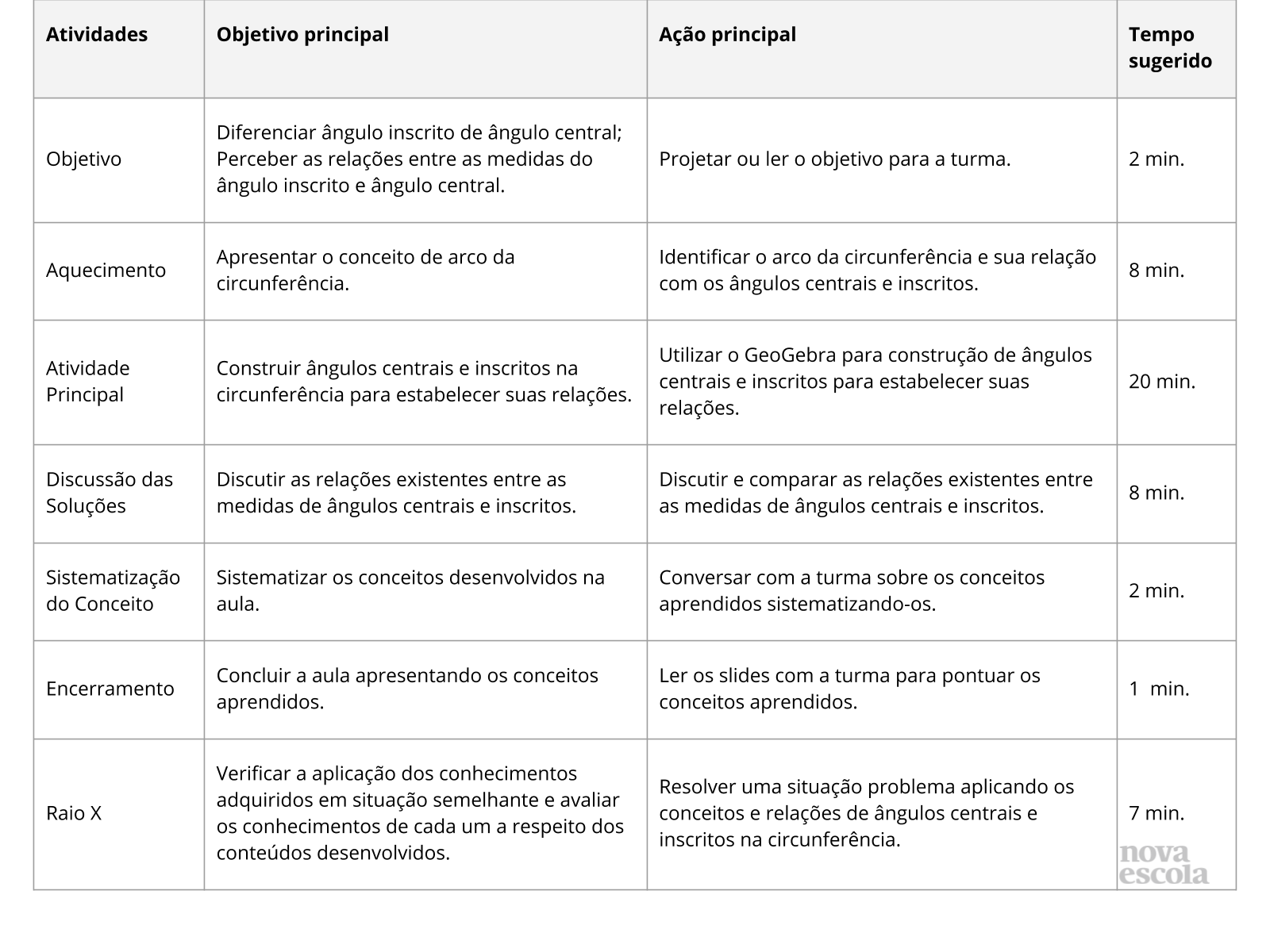
Atividade principal
Plano de Aula
Plano de aula: Descobrindo as relações entre ângulos com auxílio do Geogebra
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Ângulos na circunferência
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Renata Gerhardt Gomes Roza
Mentor: Lara Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
EF09MA11 - Resolver problemas por meio do estabelecimento de relações entre arcos, ângulos centrais e ângulos inscritos na circunferência, fazendo uso, inclusive, de softwares de geometria dinâmica.
Objetivos específicos
Diferenciar ângulo inscrito de ângulo central; Perceber as relações entre as medidas do ângulo inscrito e ângulo central.
Conceito-chave
Estabelecer as relações entre as medidas dos ângulos central e inscrito estabelecidos no mesmo arco da circunferência.
Conhecimentos Prévios
Determinar medidas da abertura de ângulos, por meio de transferidor e/ou tecnologias digitais.
Recursos necessários
- Laboratório de informática ou computadores em sala de aula.
- Download do Programa Geogebra
- Atividade Principal Impressa
- Raio X impresso
Habilidades BNCC:
Objetivos de aprendizagem
Diferenciar ângulo inscrito de ângulo central; Perceber as relações entre as medidas do ângulo inscrito e ângulo central.
Resumo da Aula
Para esta aula você irá precisar de um laboratório de informática ou solicitar que os alunos levem seus computadores para a sala de aula, essa solicitação pode ser para grupos. Oriente-os a baixar o GeoGebra antes da aula para que possam realizar a atividade.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Apresentar o objetivo para que fique claro o que se deseja atingir com essa aula.
Aquecimento

Tempo sugerido: 8 minutos. (slides 3, 4 e 5).
Orientações:
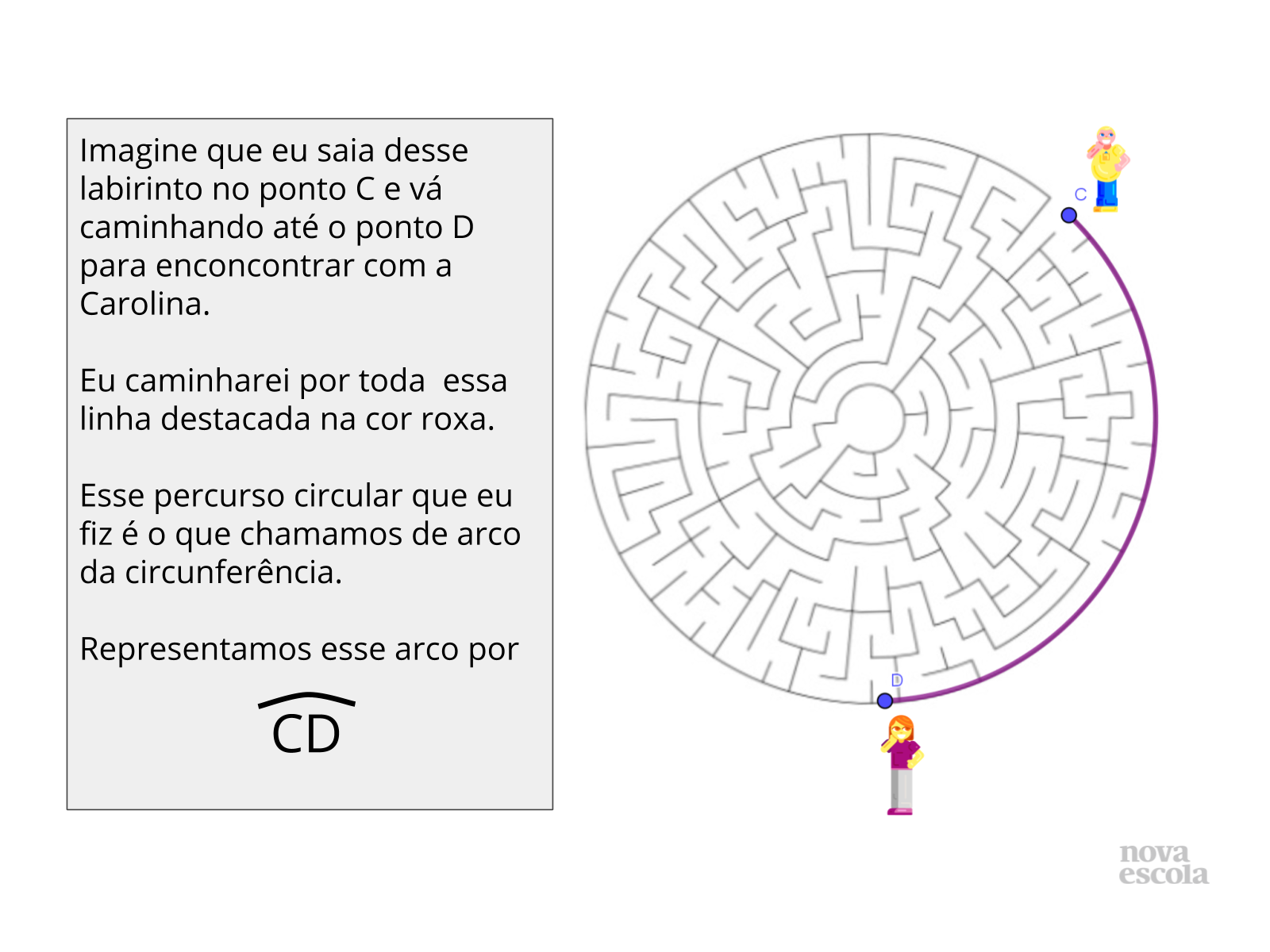
Apresente o conceito de arco da circunferência para os alunos. Leia o slide com eles e converse sobre a utilização deste conceito no nosso dia a dia e na solução de problemas matemáticos.
Peça a alguns alunos para representarem no quadro o que acham ser o arco da circunferência.
Propósito: Apresentar o conceito de arco da circunferência.
Discuta com a turma:
- Com esta apresentação formal, alguém consegue nos mostrar um arco da circunferência?
- Será que utilizamos esta ideia em nosso dia a dia?
- Em que situações precisamos medir apenas o arco da circunferência e não a circunferência completa?
Aquecimento
Tempo sugerido: 8 minutos. (slides 3, 4 e 5).
Orientações: Converse com os alunos sobre outras situações em que fazemos movimentos circulares, como pistas circulares de corrida, meia volta, até a borda de uma fatia de pizza.
Este conceito será muito importante para a conclusão da Atividade principal. É importante que a turma compreenda bem o conceito para aplicá-lo na próxima atividade.
Propósito: Apresentar o conceito de arco da circunferência.
Discuta com a turma:
- Será que utilizamos esta ideia em nosso dia a dia?
- Em que situações precisamos medir apenas o arco da circunferência e não a circunferência completa?
Aquecimento
Tempo sugerido: 8 minutos. (slides 3, 4 e 5).
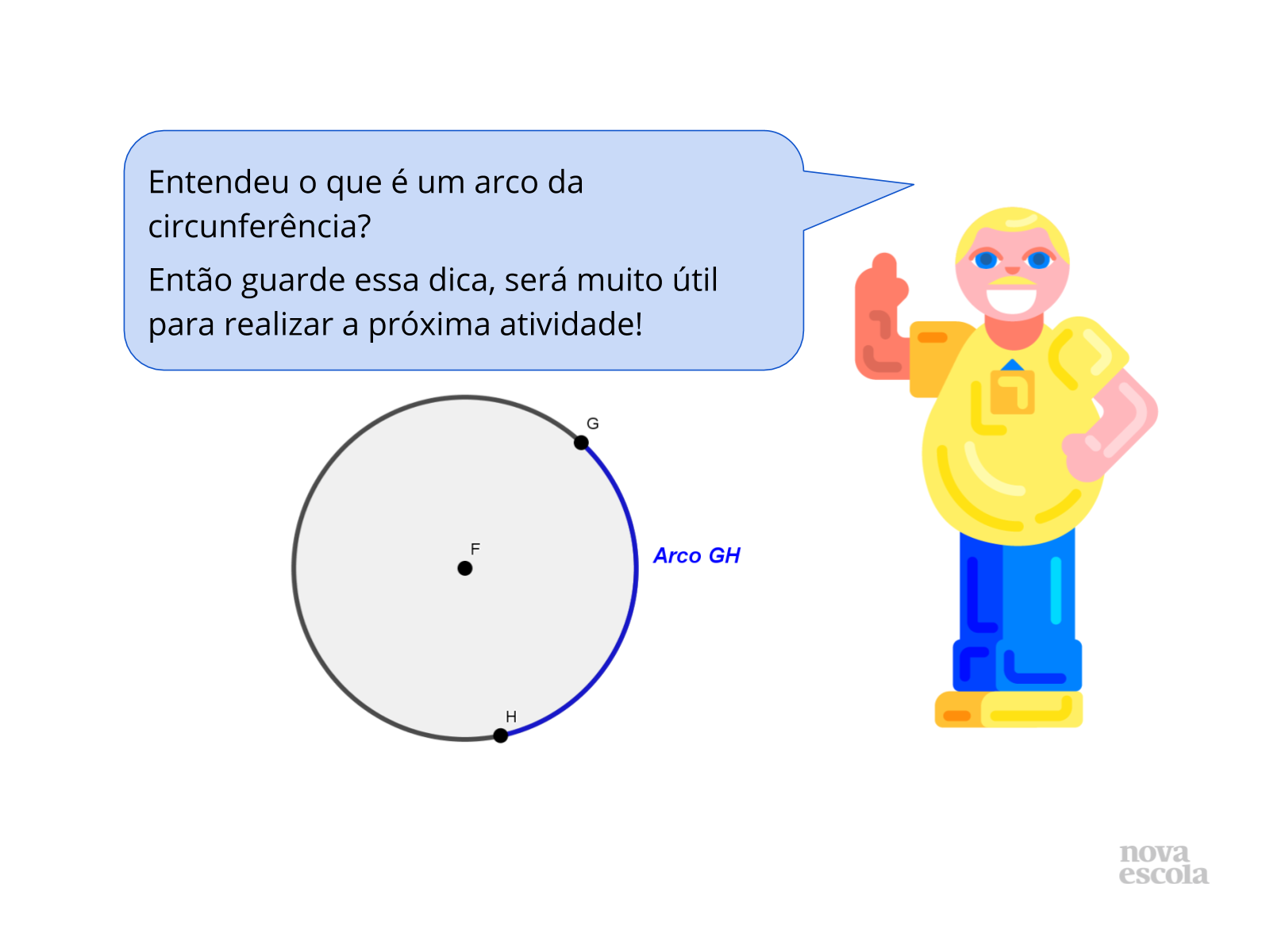
Orientações:
Enfatize com a turma a importância desse conceito e avisem que devem guardar essa dica pois ela será importante para estabelecer as relações necessárias na Atividade Principal.
É importante dizer aos alunos, que a parte que está em preto na circunferência também pode ser chamado de arco AB.
Propósito: Apresentar o conceito de arco da circunferência.
Atividade Principal
Tempo sugerido: 20 minutos. (slides 8, 9, 10, 11, 12 e 13).
Orientações:
Antes de realizar essa atividade, certifique-se que o GeoGebra já esteja instalado em todos os computadores que serão utilizados e funcionando perfeitamente. Essa atividade pode ser realizada em duplas ou em grupos caso não haja computadores disponíveis para todos os alunos.
Converse um pouco com os alunos sobre o GeoGebra, suas funções e apresente alguns recursos aos alunos. É importante que você conheça o programa antes de aplicar a atividade.
Está disponível neste plano um tutorial sobre como realizar essa atividade no geogebra, ele serve de apoio ao professor, mas também pode ser apresentado aos alunos.
Abaixo nos materiais complementares você pode encontrar o link para download do programa.
Caso não seja possível realizar esta atividade no Geogebra, apresento no Guia de intervenções uma sugestão.
Propósito: Compreender a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Materiais complementares para impressão
Resolução da Atividade Principal
Imagens para Guia de Intervenção
Tutorial Atividade Principal
Atividade Principal

Tempo sugerido: 20 minutos. (slides 8, 9, 10, 11, 12 e 13).
Orientações:
Converse um pouco com os alunos sobre o GeoGebra, suas funções e apresente alguns recursos aos alunos. É importante que você conheça o programa antes de aplicar a atividade.
Abaixo nos materiais complementares você pode encontrar o link para download do programa.
Caso não seja possível realizar esta atividade no GeoGebra, apresento no Guia de intervenções uma sugestão.
Essa atividade deverá ser realizada no laboratório de informática, ou se possível com notebook dos alunos em sala de aula, já que não é necessário conexão. Leia os orientações uma a uma com os alunos, e a cada tópico peça que vão construindo, isso facilitará a compreensão dos alunos e a realização da atividade.
Circule pela sala para garantir que os alunos estão realizando as construções corretamente.
Professora, caso os alunos apresentem dúvidas na construção da circunferência, apresento aqui o protocolo de construção do GeoGebra que pode auxiliar no desenvolvimento da atividade.
Propósito: Compreender a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Atividade Principal

Tempo sugerido: 20 minutos. (slides 8, 9, 10, 11, 12 e 13).
Orientações:
Converse com as alunos sobre as infinitas possibilidades de imagens que podem ser construídas, embora ficarão parecidas com a do slide é possível que as medidas dos ângulos sejam diferentes e inclusive a localização dos pontos. As construções diferentes vão enriquecer a atividade permitindo que os alunos comparem seus resultados, discutam as possibilidades e cheguem às suas conclusões, com a intervenção do professor.
Circule pela sala e verifique se os alunos estão compreendendo bem a atividade.
Propósito: Compreender a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discuta com a turma:
- Qual destes é o ângulo central?
- Qual ponto representa o vértice do ângulo central?
- Qual destes é o ângulo inscrito?
- Que ponto representa o vértice do ângulo inscrito?
- Que ponto representa o centro da circunferência?
- Em que arco da circunferência estão inscritos os ângulos central e inscrito?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 8, 9, 10, 11, 12 e 13).
Orientações:
Converse com as alunos sobre as infinitas possibilidades de imagens que podem ser construídas, embora ficarão parecidas com a do slide é possível que as medidas dos ângulos sejam diferentes e inclusive a localização dos pontos. As construções diferentes vão enriquecer a atividade permitindo que os alunos comparem seus resultados, discutam as possibilidades e cheguem às suas conclusões, com a intervenção do professor.
Circule pela sala e verifique se os alunos estão compreendendo bem a atividade.
Propósito: Compreender a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discuta com a turma:
- Qual destes é o ângulo central?
- Qual ponto representa o vértice do ângulo central?
- Qual destes é o ângulo inscrito?
- Que ponto representa o vértice do ângulo inscrito?
- Que ponto representa o centro da circunferência?
- Em que arco da circunferência estão inscritos os ângulos central e inscrito?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 8, 9, 10, 11, 12 e 13).
Orientações: Oriente os alunos que essa medida é a primeira que eles obtiveram na construção, antes de realizar o movimento sugerido nos próximos slides.
Propósito: Compreender a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discuta com a turma:
- Com essa imagem já é possível fazer alguma relação entre os ângulos central e inscrito?
- Aliás será que existe alguma relação possível entre eles?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 8, 9, 10, 11, 12 e 13).
Orientações:Circule pela sala orientando os alunos a fazerem as movimentações corretas e a utilizarem corretamente as funções do Geogebra.
Nesse momento. Caso os alunos tenham dúvida sobre os movimentos o tutorial da atividade pode ajudar na realização da mesma.
Propósito: Compreender a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discuta com a turma:
- Ao realizarmos estes movimentos, é possível perceber alguma relação?
- Isso acontece com qualquer ângulo inscrito na circunferência?
- E se criamos outros dois pontos, diferentes de C e D, e neles apenas criarmos um ângulo inscrito no mesmo vértice E. É possível estabelecermos as mesmas relações?
- Se modificar os raios, modificamos também os ângulos?
Atividade Principal

Tempo sugerido: 20 minutos. (slides 8, 9, 10, 11, 12 e 13).
Orientações: Peça que os alunos compartilhem seus resultados com os colegas e discutam sobre as conclusões que chegaram, analisando se com os resultados dos colegas é possível chegar às mesmas conclusões.
Propósito: Compreender a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discuta com a turma:
- Compare todas as medidas registradas na tabela, o que podemos afirmar sobre elas?
- Se alterarmos apenas a medida de um dos ângulos, o outro ângulo permanece com a mesma medida?
- Se criarmos um outro ângulo inscrito com vértice diferente, mas inscrito no mesmo arco, as relações permanecem?
- Compare seus resultados com o de seus colegas e verifique se chegaram às mesmas conclusões.
Discussão das Soluções
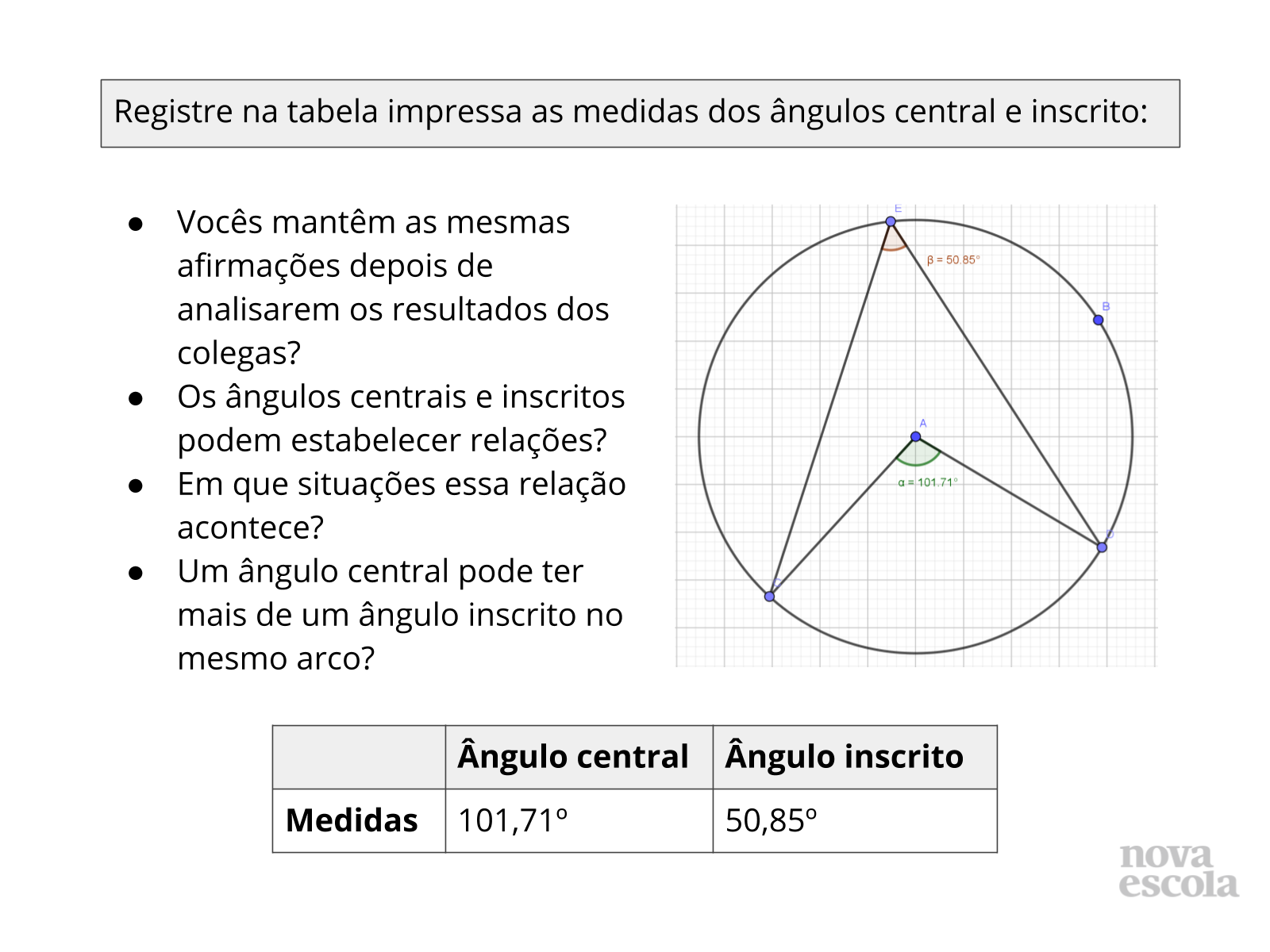
Tempo sugerido: 8 minutos. (slides 13 ao 21 ).
Orientações: Esse momento da sua aula é muito importante, os alunos vão refletir sobre suas análises e suas respostas, peça aos alunos que troquem seus resultados com o de seus colegas e realizem o mesmo teste que fizeram em suas próprias atividades.
Questione-os se ainda assim é possível fazer as mesmas afirmações.
Propósito: Discutir a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discussão das Soluções
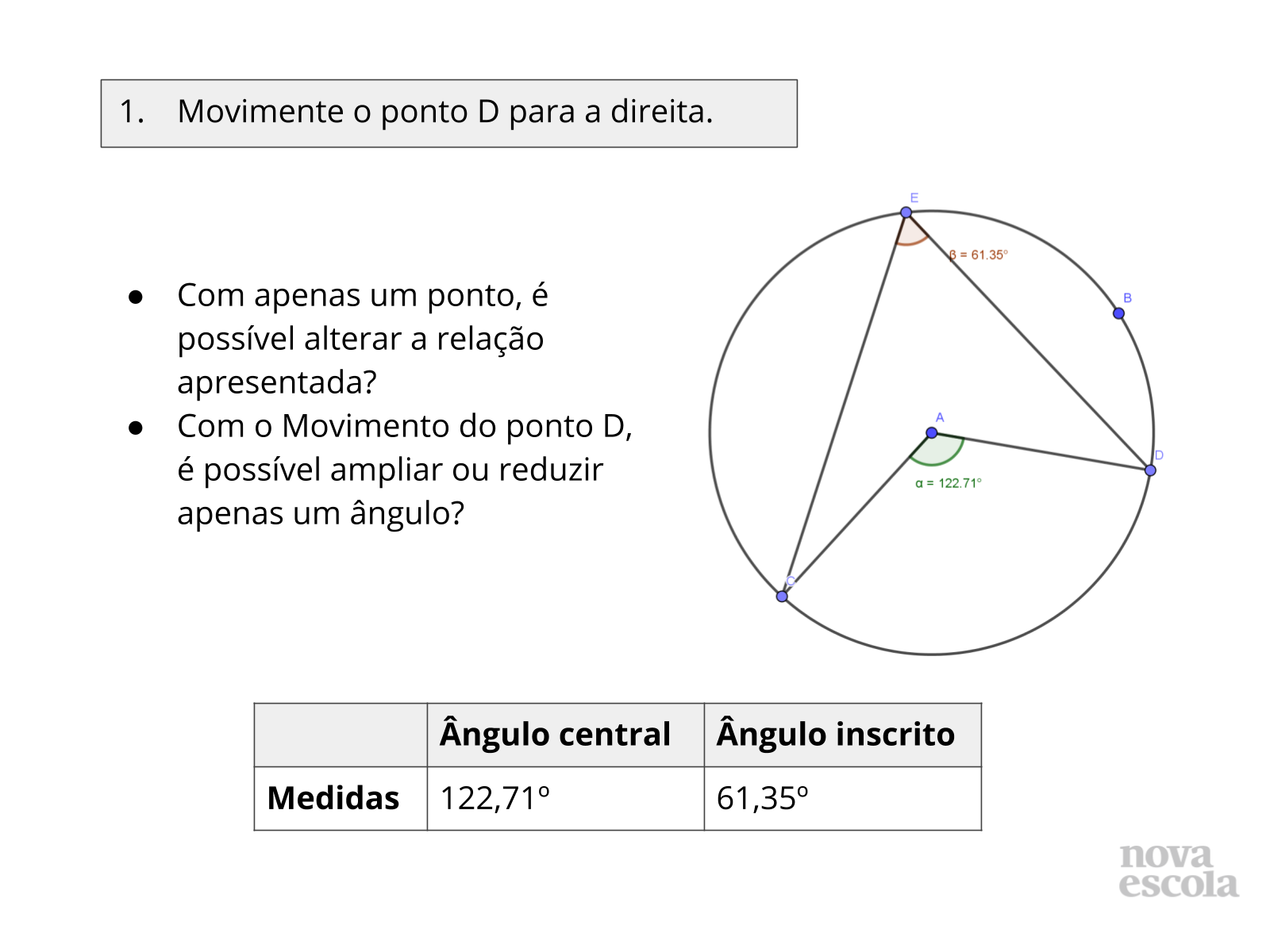
Tempo sugerido: 8 minutos. (slides 13 ao 21 ).
Orientações:
Esse momento da sua aula é muito importante, os alunos vão refletir sobre suas análises e suas respostas, peça aos alunos que troquem seus resultados com o de seus colegas e realizem o mesmo teste que fizeram em suas próprias atividades.
Questione-os se ainda assim é possível fazer as mesmas afirmações.
Propósito: Discutir a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discussão das Soluções
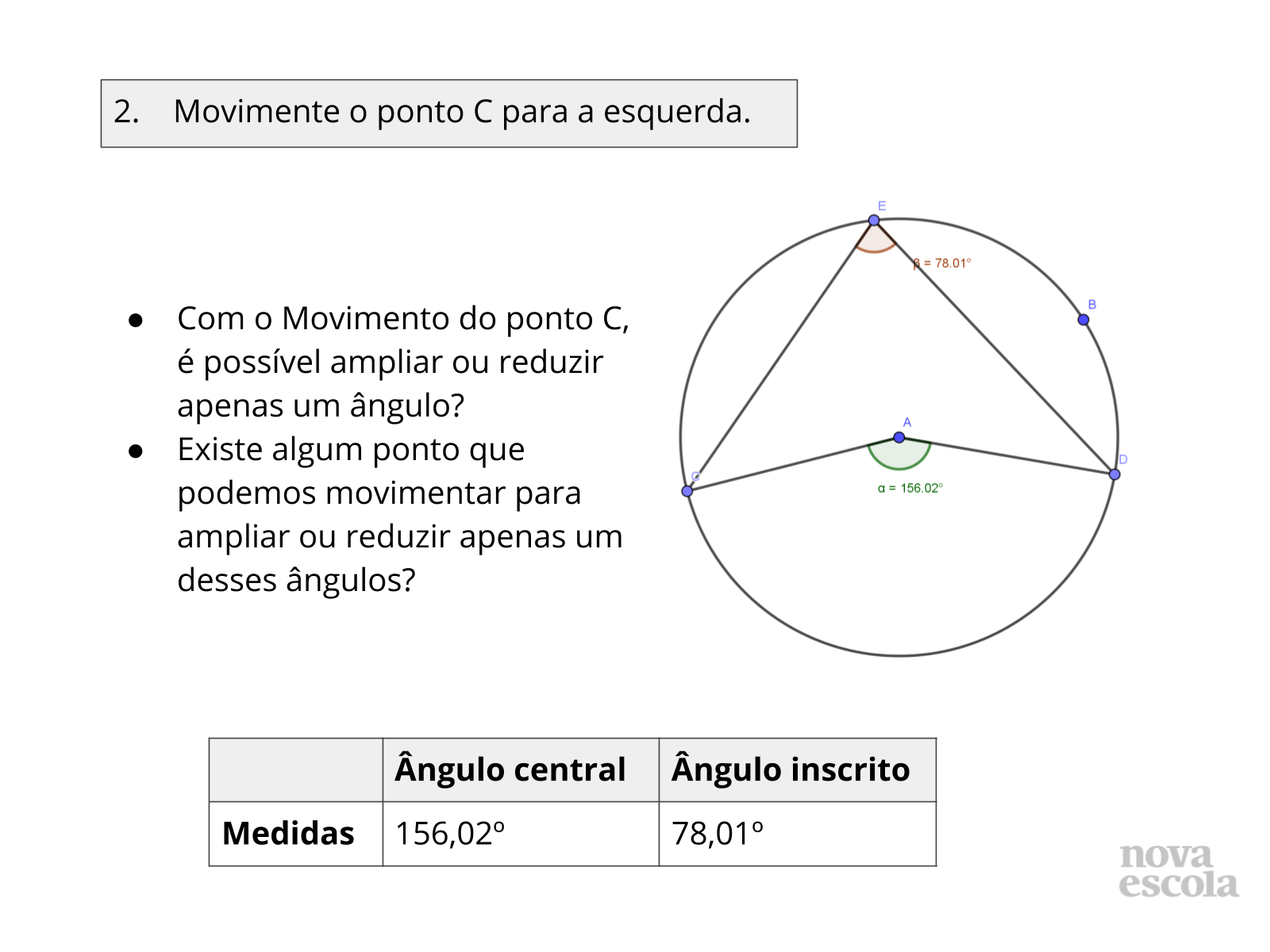
Tempo sugerido: 8 minutos. (slides 13 ao 21 ).
Orientações: Esse momento da sua aula é muito importante, os alunos vão refletir sobre suas análises e suas respostas, peça aos alunos que troquem seus resultados com o de seus colegas e realizem o mesmo teste que fizeram em suas próprias atividades.
Questione-os se ainda assim é possível fazer as mesmas afirmações.
Propósito: Discutir a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discussão das Soluções
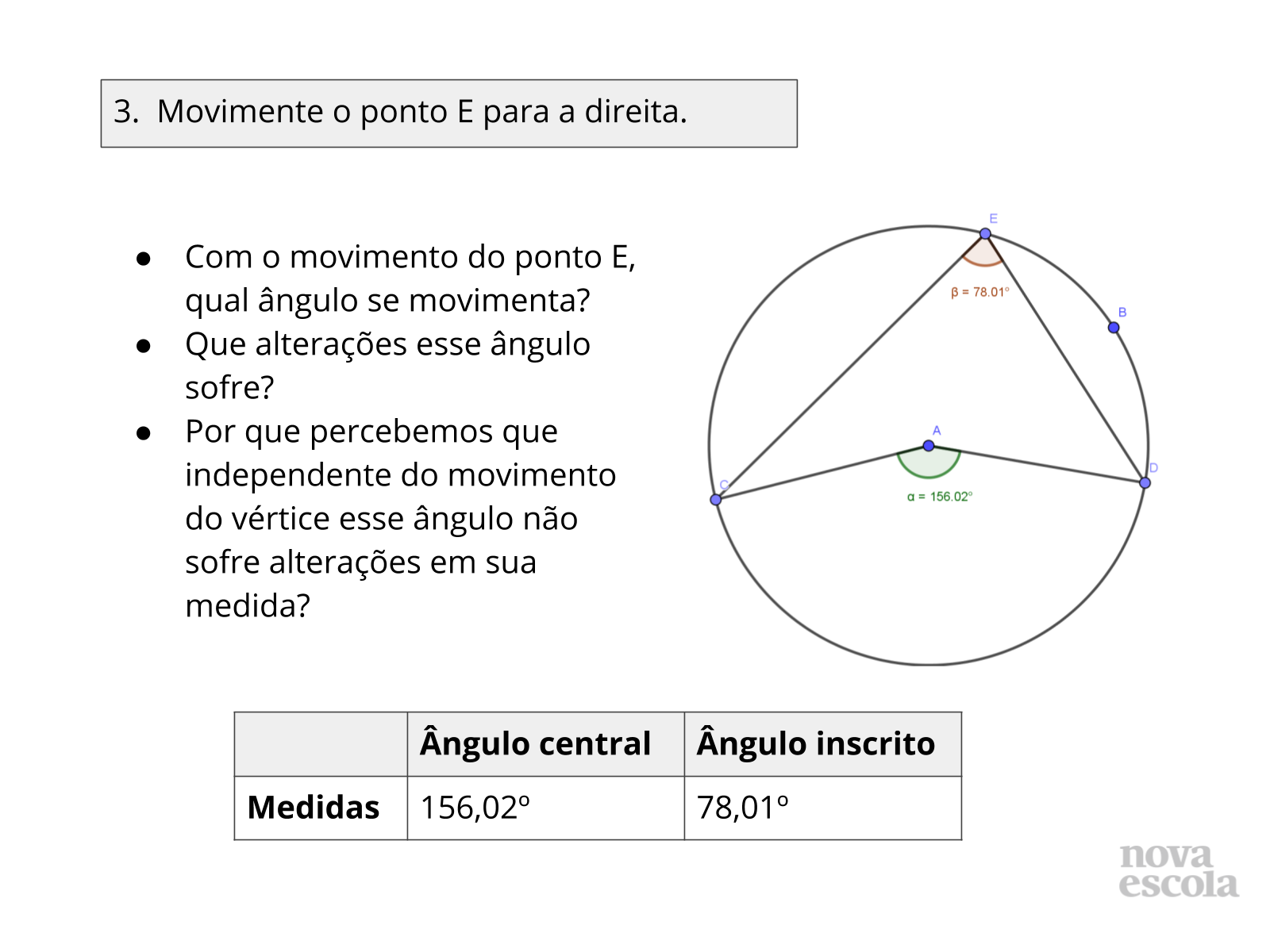
Tempo sugerido: 8 minutos. (slides 13 ao 21 ).
Orientações: Esse momento da sua aula é muito importante, os alunos vão refletir sobre suas análises e suas respostas, peça aos alunos que troquem seus resultados com o de seus colegas e realizem o mesmo teste que fizeram em suas próprias atividades.
Questione-os se ainda assim é possível fazer as mesmas afirmações.
Propósito: Discutir a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discussão das Soluções
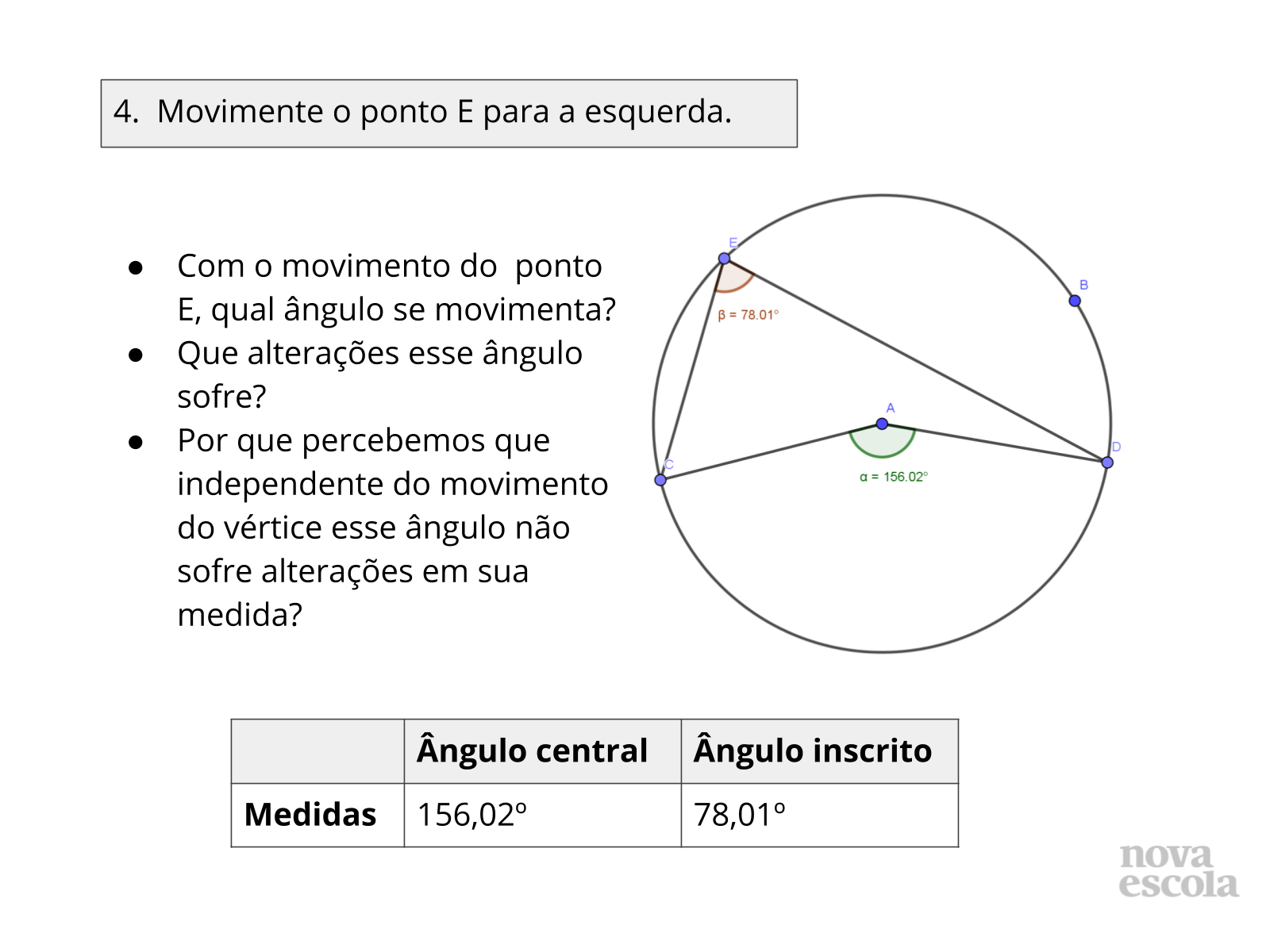
Tempo sugerido: 8 minutos. (slides 13 ao 21 ).
Orientações: Esse momento da sua aula é muito importante, os alunos vão refletir sobre suas análises e suas respostas, peça aos alunos que troquem seus resultados com o de seus colegas e realizem o mesmo teste que fizeram em suas próprias atividades.
Questione-os se ainda assim é possível fazer as mesmas afirmações.
É importante lembrar com os alunos que os ângulos não podem ser descaracterizados, portanto, é preciso ter cuidado com os movimentos. Sendo assim, o vértice não pode estar abaixo no semi círculo onde se forma o ângulo central. E abertura do ângulo central não deve ser maior que 180º. Pois assim, o ângulo central passa a ser o menor que este formado no centro.
Propósito: Discutir a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discussão das Soluções
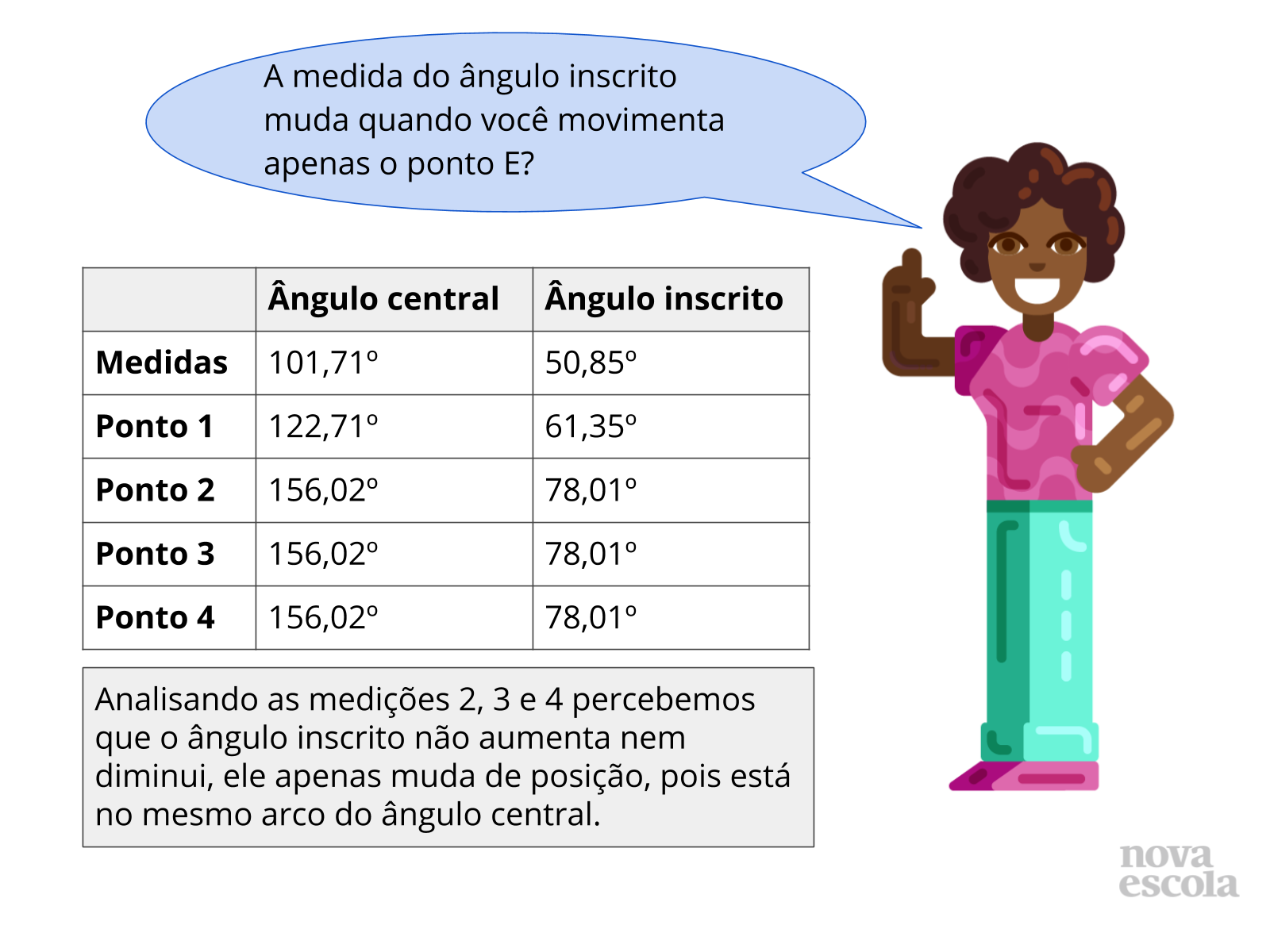
Tempo sugerido: 8 minutos. (slides 13 ao 21 ).
Orientações: Esse momento da sua aula é muito importante, os alunos vão refletir sobre suas análises e suas respostas, peça aos alunos que troquem seus resultados com o de seus colegas e realizem o mesmo teste que fizeram em suas próprias atividades.
Questione-os se ainda assim é possível fazer as mesmas afirmações.
Propósito: Discutir a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discuta com a turma:
Depois que os grupos trocarem seus resultados, questione sobre as possibilidades:
- Essa conclusão serve para quaisquer ângulos inscritos e centrais que estejam no mesmo arco?
- É possível encontrar outros ângulos inscritos no mesmo arco? Se sim, vamos Construí-los?
Discussão das Soluções
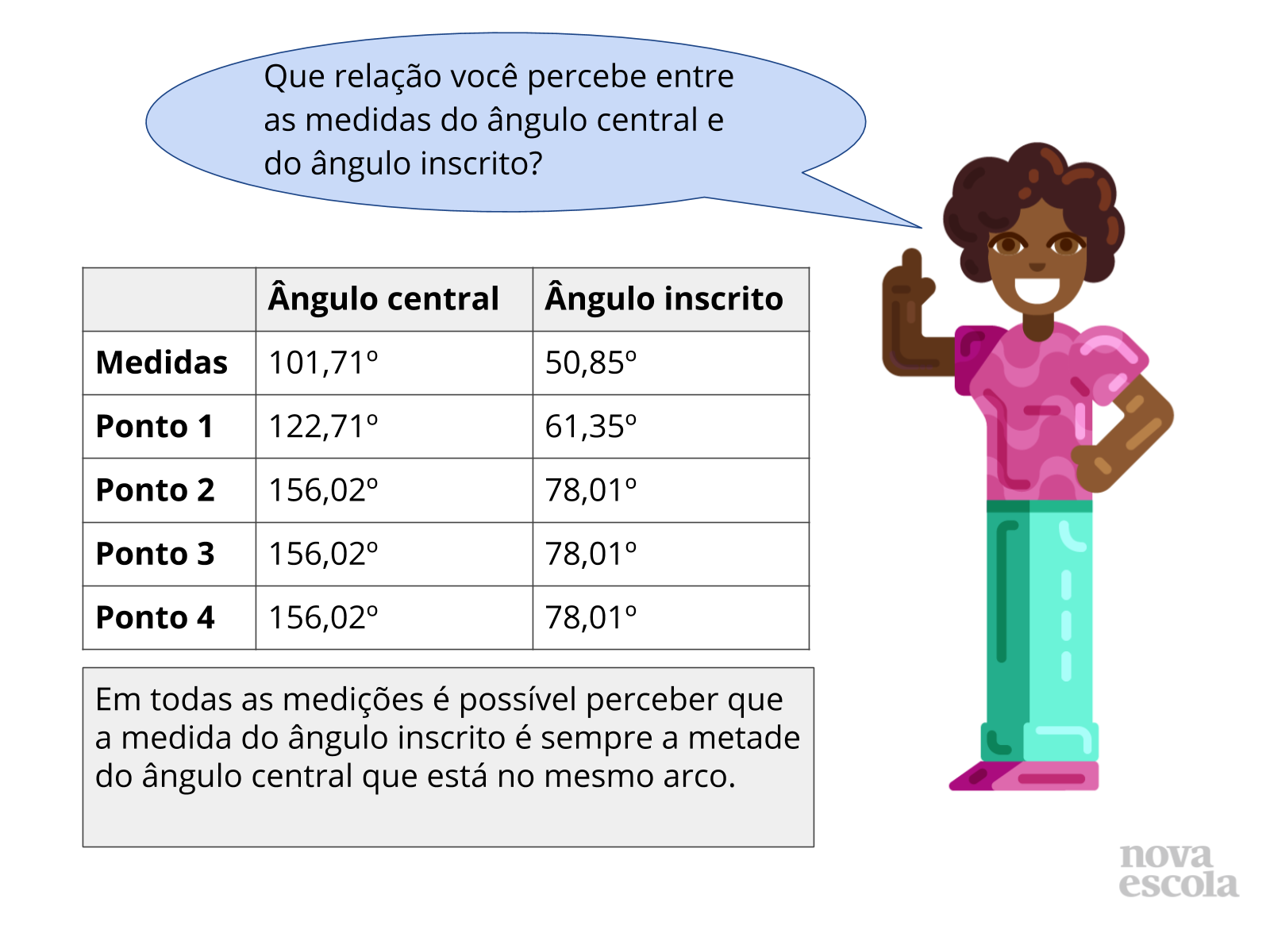
Tempo sugerido: 8 minutos. (slides 13 ao 21 ).
Orientações: Esse momento da sua aula é muito importante, os alunos vão refletir sobre suas análises e suas respostas, peça aos alunos que troquem seus resultados com o de seus colegas e realizem o mesmo teste que fizeram em suas próprias atividades.
Questione-os se ainda assim é possível fazer as mesmas afirmações.
É importante ressaltar com os alunos que o GeoGebra está fornecendo até a segunda casa decimal, o que por arredondamento pode influenciar no valor do dobro ou metade. Na aba opções é possível alterar o número de casa decimais, é importante realizar esse exercício com os alunos para que os mesmo cheguem à conclusão que a medida do ângulo inscrito é a metade do ângulo central inscrito no mesmo arco.
Propósito: Discutir a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discuta com a turma:
Depois que os grupos trocarem seus resultados, questione sobre as possibilidades:
- Essa conclusão serve para quaisquer ângulos inscritos e centrais que estejam no mesmo arco?
- É possível encontrar outros ângulos inscritos no mesmo arco? Se sim, vamos Construí-los?
Discussão das Soluções
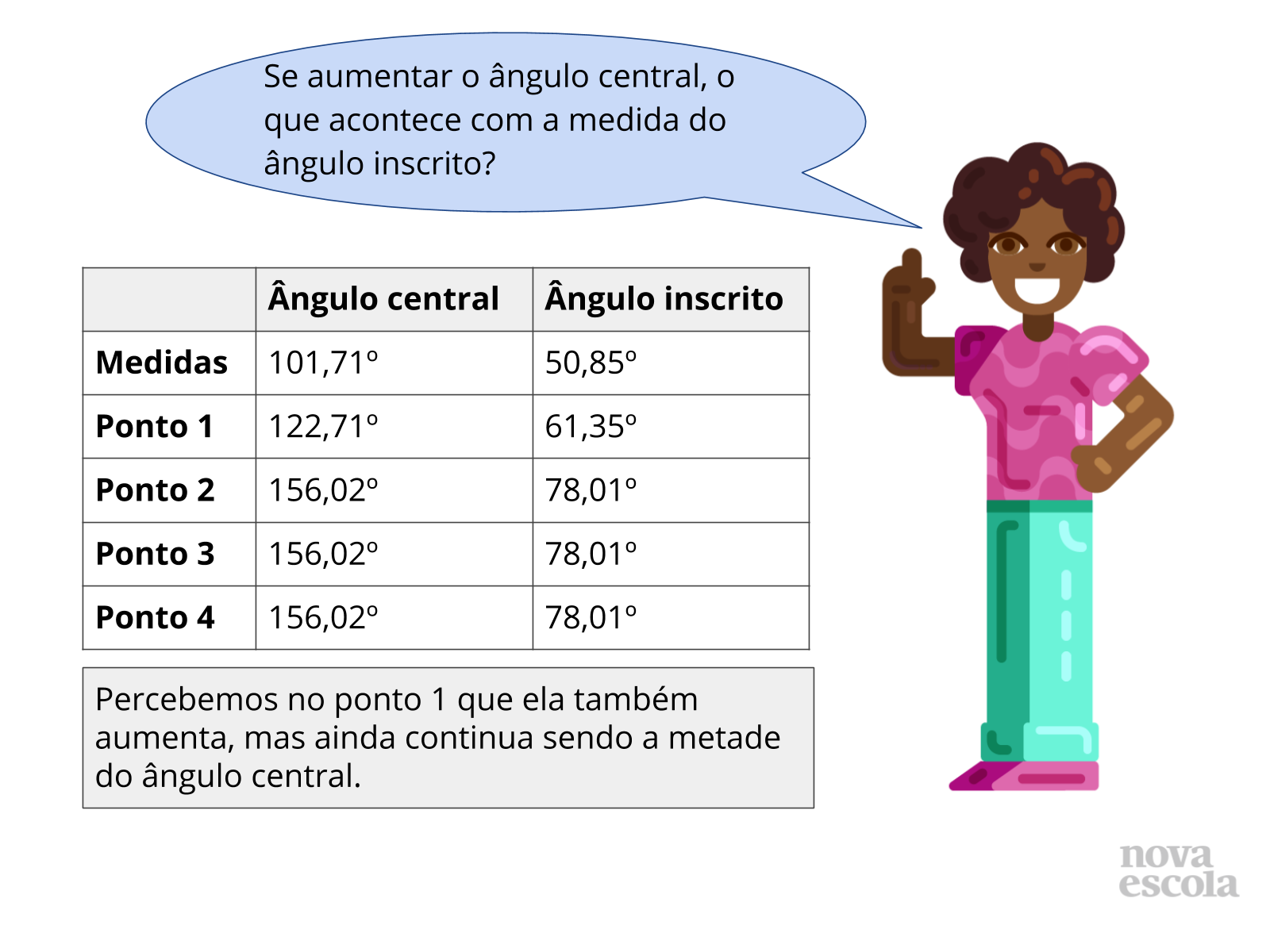
Tempo sugerido: 8 minutos. (slides 13 ao 21 ).
Orientações:
Esse momento da sua aula é muito importante, os alunos vão refletir sobre suas análises e suas respostas, peça aos alunos que troquem seus resultados com o de seus colegas e realizem o mesmo teste que fizeram em suas próprias atividades.
Questione-os se ainda assim é possível fazer as mesmas afirmações.
Propósito: Discutir a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discuta com a turma:
Depois que os grupos trocarem seus resultados, questione sobre as possibilidades:
- Essa conclusão serve para quaisquer ângulos inscritos e centrais que estejam no mesmo arco?
- É possível encontrar outros ângulos inscritos no mesmo arco? Se sim, vamos Construí-los?
Discussão das Soluções
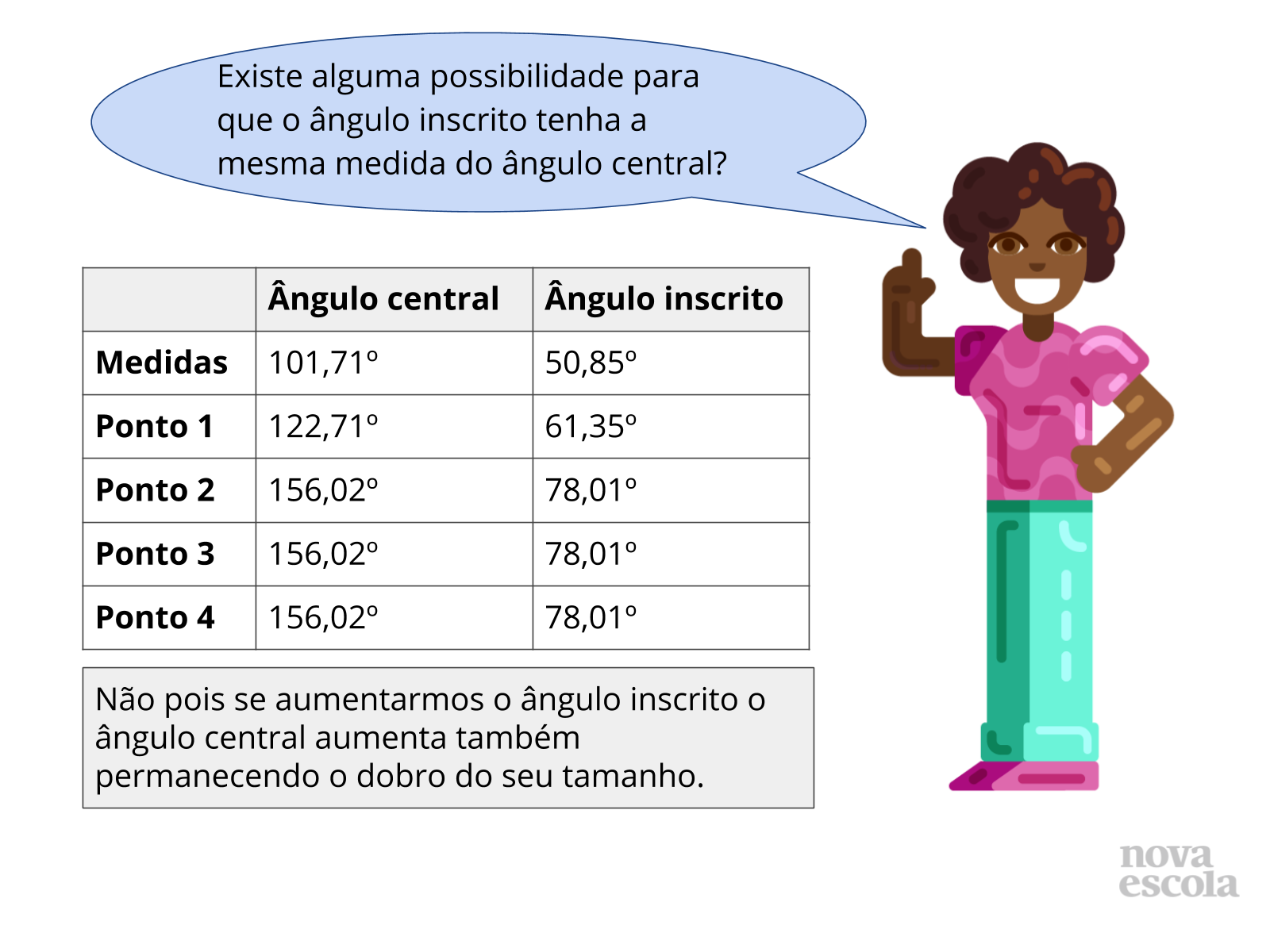
Tempo sugerido: 8 minutos. (slides 13 ao 21 ).
Orientações: Esse momento da sua aula é muito importante, os alunos vão refletir sobre suas análises e suas respostas, peça aos alunos que troquem seus resultados com o de seus colegas e realizem o mesmo teste que fizeram em suas próprias atividades.
Questione-os se ainda assim é possível fazer as mesmas afirmações.
Propósito: Discutir a relação entre as medidas do ângulo central e ângulo inscrito em uma mesma circunferência e no mesmo arco.
Discuta com a turma:
Depois que os grupos trocarem seus resultados, questione sobre as possibilidades:
- Essa conclusão serve para quaisquer ângulos inscritos e centrais que estejam no mesmo arco?
- É possível encontrar outros ângulos inscritos no mesmo arco? Se sim, vamos Construí-los?
Sistematização do Conceito

Tempo sugerido: 2 minutos.
Orientações: Leia com os alunos as afirmações do slide e solicite que registrem em seus cadernos as definições apresentadas.
Propósito: Sistematizar os conceitos trabalhados nessa aula e apresentar aos alunos.
Encerramento

Tempo sugerido: 1 minuto.
Orientações: Leia com os alunos as afirmações do slide e solicite que registrem em seus cadernos as definições apresentadas.
Propósito: Concluir a aula apresentação os conceitos aprendidos.
Raio X
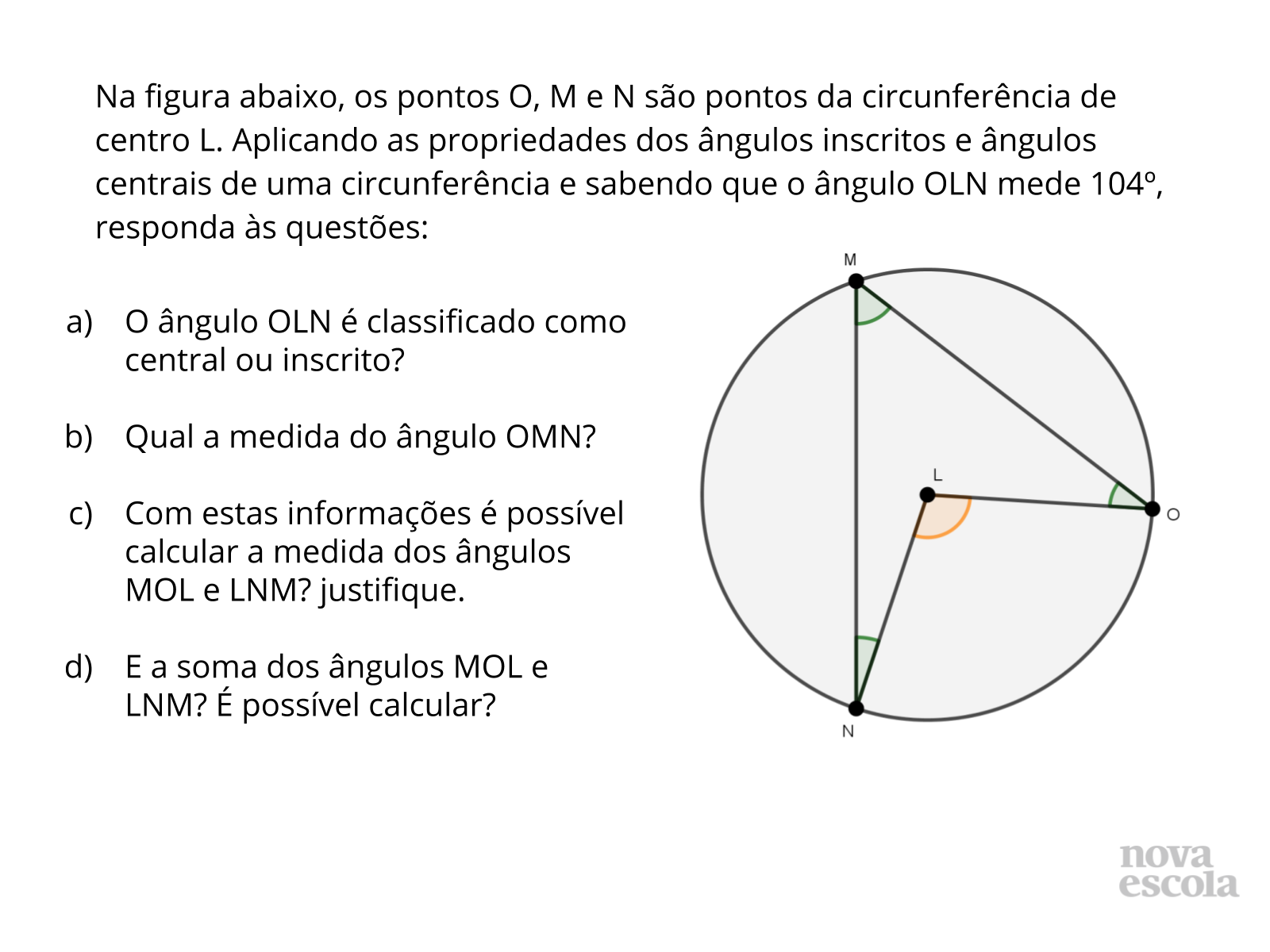
Tempo sugerido: 8 minutos.
Orientações: Peça que individualmente, leiam a atividade e a realizem. Circule para verificar como os alunos estão realizando a atividade e se ainda possuem dúvidas.
Propósito: Verificar se os alunos conseguem aplicar os conhecimentos adquiridos ao longo dessa aula.
Discuta com a turma:
- Por que com as informações dadas não é possível calcular os ângulos MOL e LNM?
- Por que é possível calcular a medida do ângulo NMO?
- Como podemos classificar esse ângulo?
Materiais complementares da impressão
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_11GEO02)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.), régua, transferidor, tesoura e papel para anotações.
- Optativas: Smartfone.
Atividade principal
- Pela rede social escolhida determine que, acessem o Geogebra (ou instalado no PC ou online pelo link https://www.geogebra.org/classic?lang=pt_PT)
- Agora solicite que sigam os passos abaixo:
1. Clique na opção para esconder os eixos e malha quadriculada.
2. Construa uma circunferência de centro A. Utilize a opção: Círculo dados centro e um de seus pontos.
3. Marque os pontos C, D e E na circunferência. (lembre-se pontos que estão na circunferência são pontos que pertencem à linha da circunferência).
4. Na opção segmentos, construa os segmentos: AC, AD, EC e ED
5. Construa o ângulo central C D, utilize a opção: ângulo selecione três pontos ou duas retas. - Mantenha o rótulo que indica a medida do ângulo e lembre-se de marcar os pontos no sentido anti-horário.
6. Construa o ângulo inscrito CÊD, utilize a opção: ângulo selecione três pontos ou duas retas.- Mantenha o rótulo que indica a medida do ângulo
- Dê um tempo para essa construção e peça para mostrarem suas construções e verifique se ficou semelhante a:

- Agora peça para movimentarem alguns pontos conforme a indicação e relatem as relações entre os ângulos central e inscrito:
1. Movimente o ponto D para a direita.
2. Movimente o ponto C para a esquerda.
3. Movimente o ponto E para a direita.
4. Movimente o ponto E para a esquerda.
5. Movimente da forma que você quiser os pontos.
Discussão das soluções, sistematização e encerramento
- Na discussão das soluções, faça-os entender que ao movimentar os vértices que estão na circunferência não muda o ângulo central nem o inscrito relativo a ele, mas ao aumentar o ângulo central também aumenta o ângulo inscrito e mantendo a relação de ser um a metade do outro.
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e incentive-os a tentar explicar o que aprenderam a eles.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Renata Gerhardt Gomes Roza
Mentor: Lara Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
EF09MA11 - Resolver problemas por meio do estabelecimento de relações entre arcos, ângulos centrais e ângulos inscritos na circunferência, fazendo uso, inclusive, de softwares de geometria dinâmica.
Objetivos específicos
Diferenciar ângulo inscrito de ângulo central; Perceber as relações entre as medidas do ângulo inscrito e ângulo central.
Conceito-chave
Estabelecer as relações entre as medidas dos ângulos central e inscrito estabelecidos no mesmo arco da circunferência.
Conhecimentos Prévios
Determinar medidas da abertura de ângulos, por meio de transferidor e/ou tecnologias digitais.
Recursos necessários
- Laboratório de informática ou computadores em sala de aula.
- Download do Programa Geogebra
- Atividade Principal Impressa
- Raio X impresso









