Resumo da aula
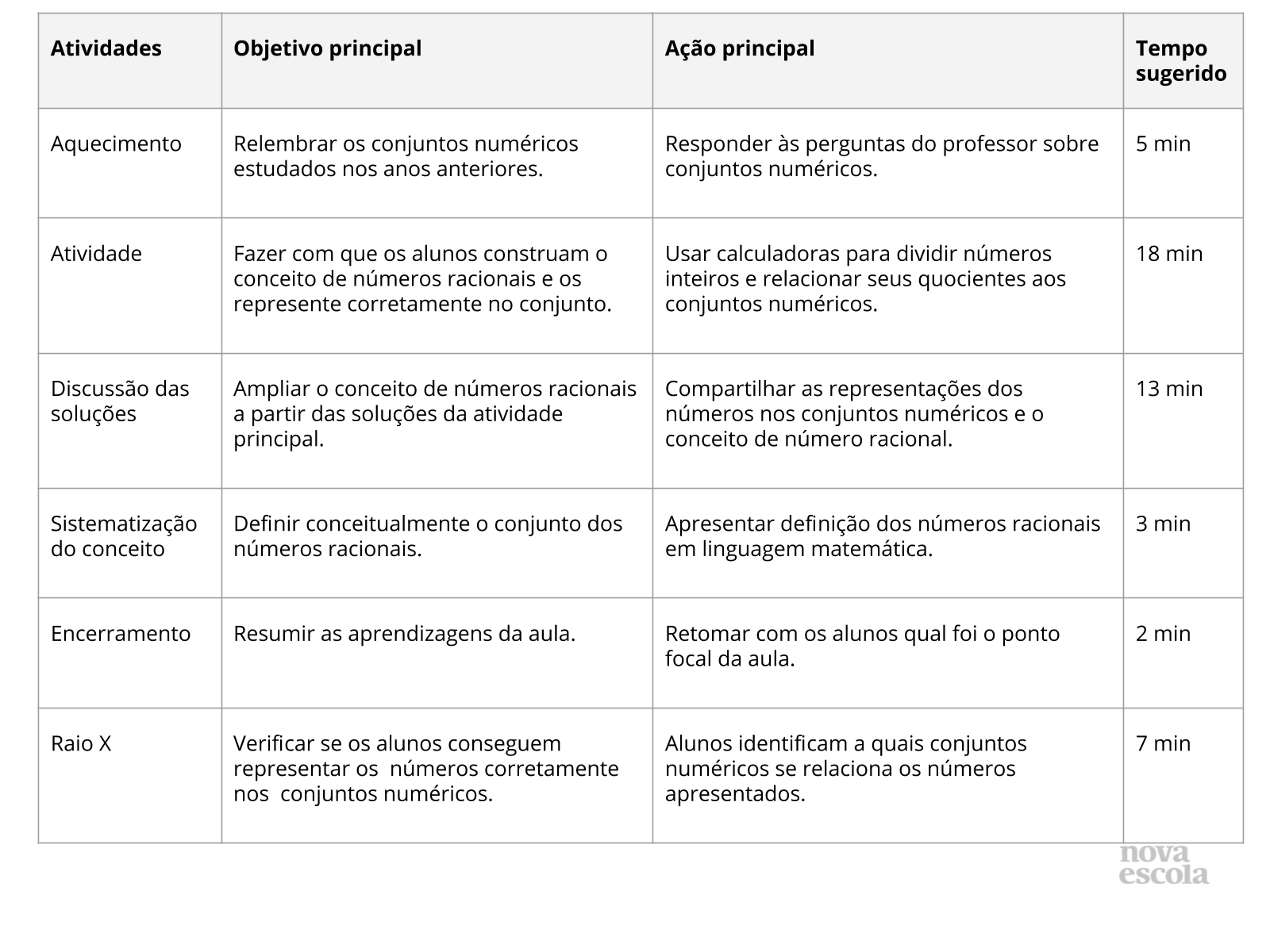
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma. Através da habilidade trabalhada nesta aula os alunos conseguirão ampliar seus conhecimentos dos números racionais, reconhecendo que podem ser apresentados também em sua forma negativa, a partir da seguinte definição: número racional é qualquer número que possa ser escrito como uma fração.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 5 minutos.
Orientação: Primeiramente, relembre os números naturais e inteiros. Após, discuta com a turma sobre o quão presente os números racionais estão no cotidiano. Em cada conjunto numérico abordado, peça apenas o exemplo de um aluno, tendo em vista que a não pode ser tirada a dificuldade da atividade principal.
Propósito: Relembrar os conjuntos numéricos N e Z estudados nos anos anteriores, exemplificando quais números podem pertencer a esses conjuntos.
Discuta com a turma:
- Em sua opinião, por que os números naturais são chamados assim?
- Em sua opinião, por que os números inteiros são chamados assim?
- Dê exemplos de números naturais e números inteiros.
- Em quais situações do cotidiano você já se deparou com números que não eram nem naturais e nem inteiros? Eles estavam em sua forma positiva ou negativa?
Atividade principal - parte 1
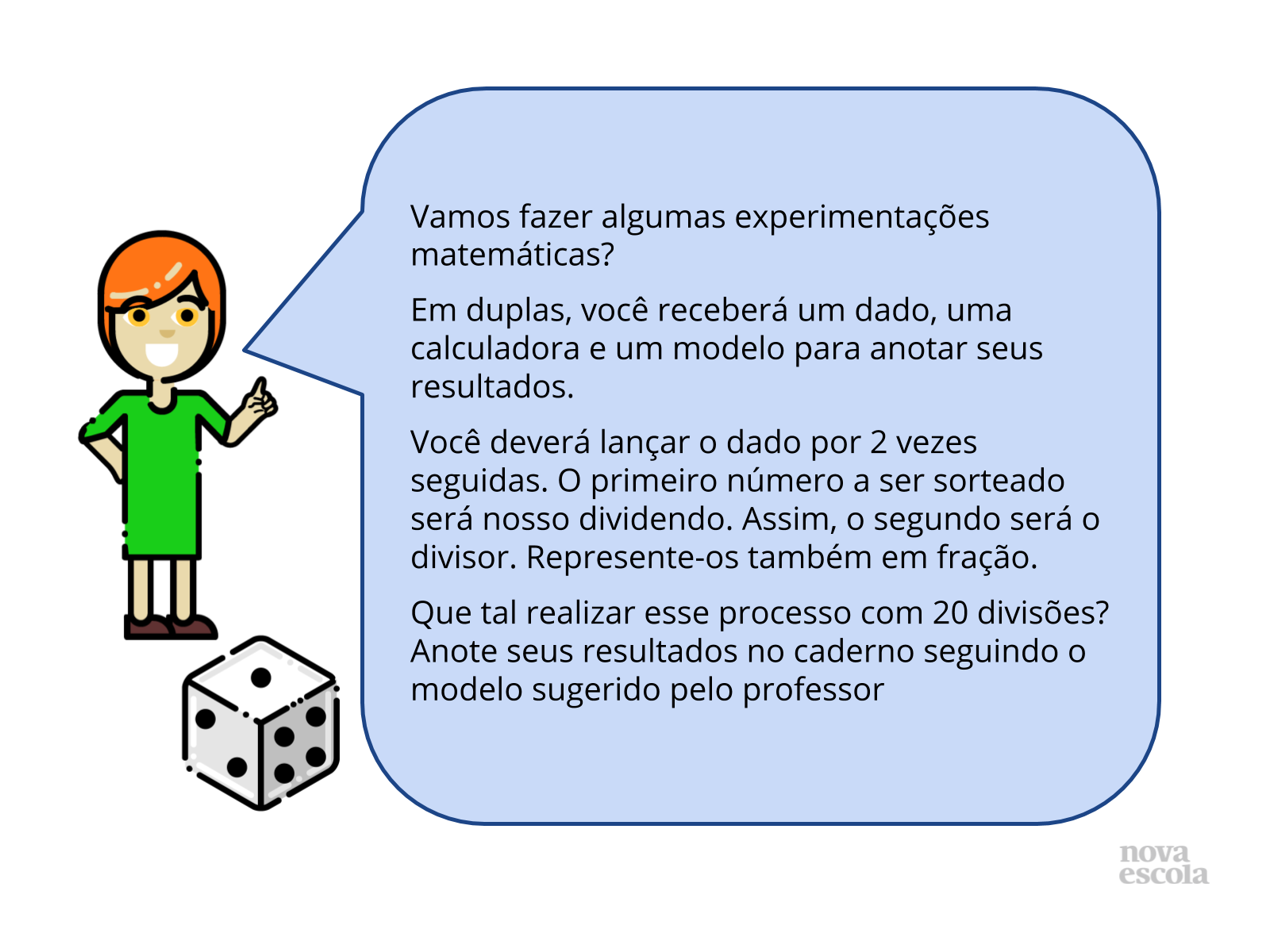
Tempo sugerido: 7 minutos.
Orientação: Previamente, organize a sala em duplas de forma estratégica. Distribua para cada dupla uma versão dos dados disponíveis neste plano (os dados, o diagrama e a tabela encontram-se no arquivo da atividade da aula) e uma calculadora (os alunos podem ser orientados previamente a trazerem a calculadora ou o celular). Também pode ser distribuído o modelo de uma tabela para registro dos cálculos (se preferir, é possível copiar o modelo no quadro para alunos reproduzirem no caderno). Circule pela sala verificando quais são os resultados obtidos pelos alunos. Caso os resultados estejam muito repetitivos, de modo a não permitir uma análise aprofundada pelos alunos, sugira divisões que resultem em quocientes de interesse (ao menos 6 quocientes decimais, sendo eles negativos e positivos; ao menos 2 quocientes naturais; ao menos 2 quocientes inteiros negativos; ao menos uma divisão por zero, que é inexistente)
Você pode fazer o download dos materiais necessários para esta atividade e imprimir para os seus alunos.
Caso não queira montar os dados, você pode colar etiquetas que contenham os números descritos na atividade, seja em dados convencionais ou quaisquer outros objetos em formato de cubo.
Utilize o guia de intervenções para analisar as dificuldades e realizar intervenções.
Propósito: Fazer com que os alunos construam o conceito de números racionais a partir de divisões com calculadora, representando adequadamente os números obtidos dentro de 3 conjuntos numéricos (natural, inteiro e racional).
Material complementar:
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade principal - parte 2
Tempo sugerido: 10 minutos.
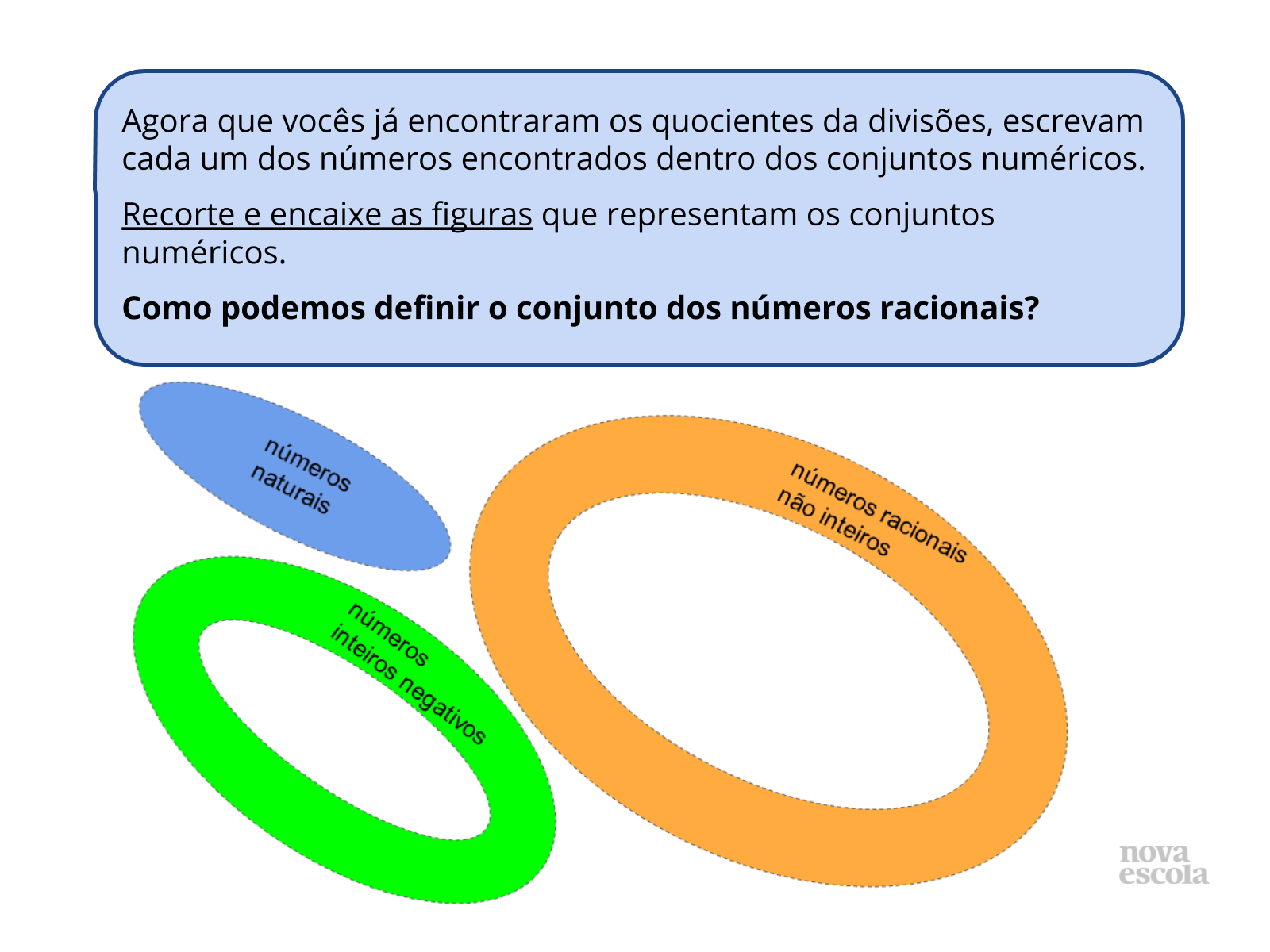
Orientação: Distribua para a cada dupla as folhas com as figuras que representam os conjuntos numéricos. Certifique que os alunos compreendam que têm de classificar os quocientes obtidos dentro de cada conjunto numérico e que, após, devem recortar as figuras e sobrepor os conjuntos, de modo a perceberem que os números naturais e inteiros também são números racionais. Por fim, devem buscar uma definição para o conjunto dos números racionais. Neste momento, a definição dos números racionais não precisa ser totalmente matemática. Circule pela sala verificando quais são as definições que estão sendo debatidas pelos alunos.
Propósito: Fazer com que os alunos construam o conceito de números racionais a partir de divisões com calculadora, representando adequadamente os números obtidos dentro de 3 conjuntos numéricos (natural, inteiro e racional).
Discussão da solução - parte I (slides 6 e 7)
Tempo sugerido: 3 minutos.
Orientação: Primeiramente, deixe os alunos compartilharem, para a sala, os quocientes das divisões e como foi realizar essa primeira parte da atividade: “houve algo inesperado?”. Depois, passe para esta série de slides, como forma de mostrar os resultados possíveis. Caso não haja projetor, você pode apenas dar alguns exemplos de quocientes possíveis.
Propósito: Compartilhar as observações feitas pelos alunos durante o processo de divisão dos números e iniciar brevemente a conceituação de número racional.
Discuta com a turma:
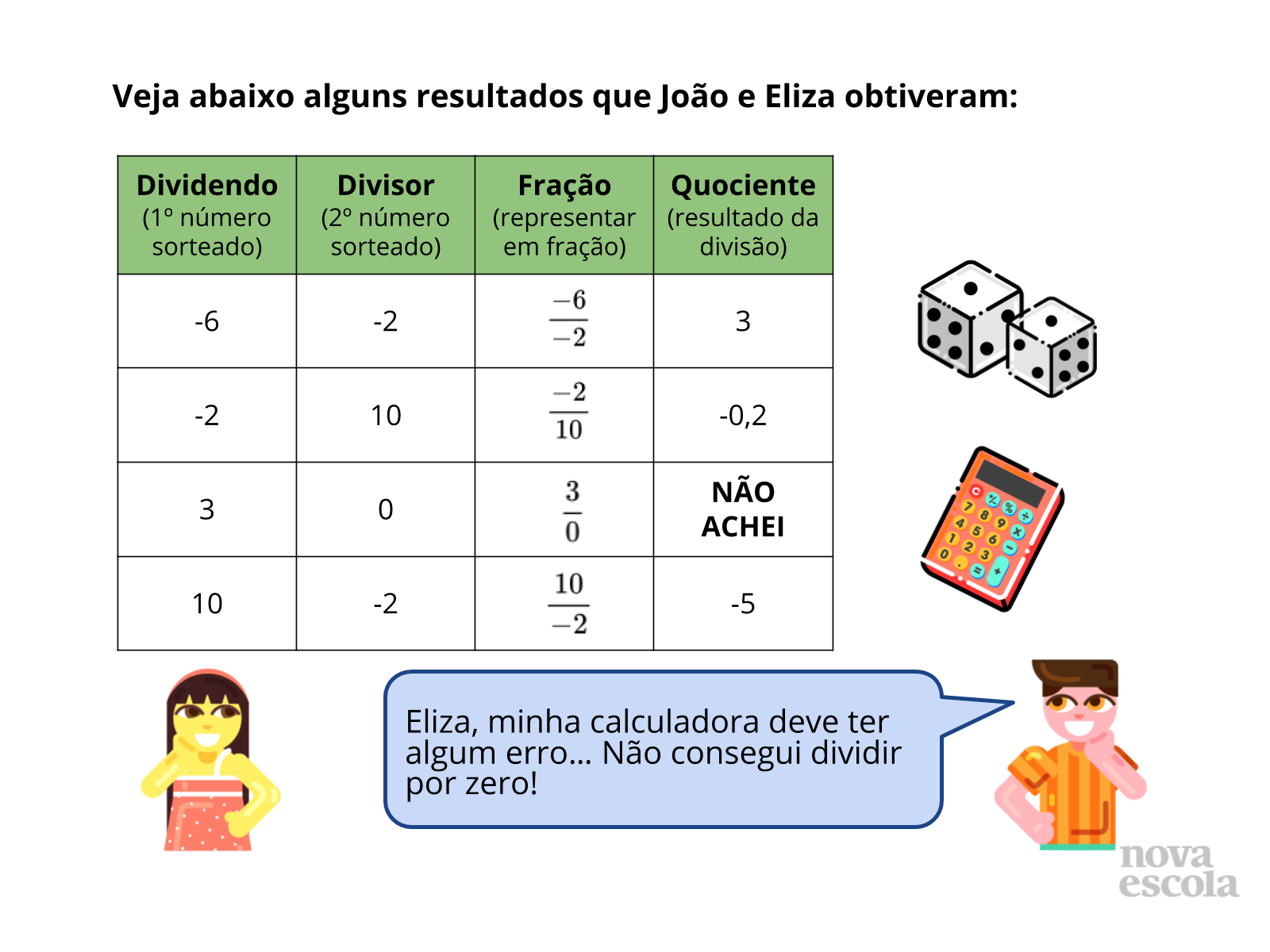
- O que aconteceu quando zero foi o segundo número sorteado? Qual foi o quociente da divisão?
- Qual fração pode representar o quociente 3? E o quociente -5?
Discussão da solução - parte I (slides 6 e 7)
Tempo sugerido: 3 minutos.
Orientação: Primeiramente, deixe os alunos compartilharem, para a sala, os quocientes das divisões e como foi realizar essa primeira parte da atividade: “houve algo inesperado?”. Depois, passe para esta série de slides, como forma de mostrar os resultados possíveis. Caso não haja projetor, você pode apenas dar alguns exemplos de quocientes possíveis.
Propósito: Compartilhar as observações feitas pelos alunos durante o processo de divisão dos números e iniciar brevemente a conceituação de número racional.
Discuta com a turma:
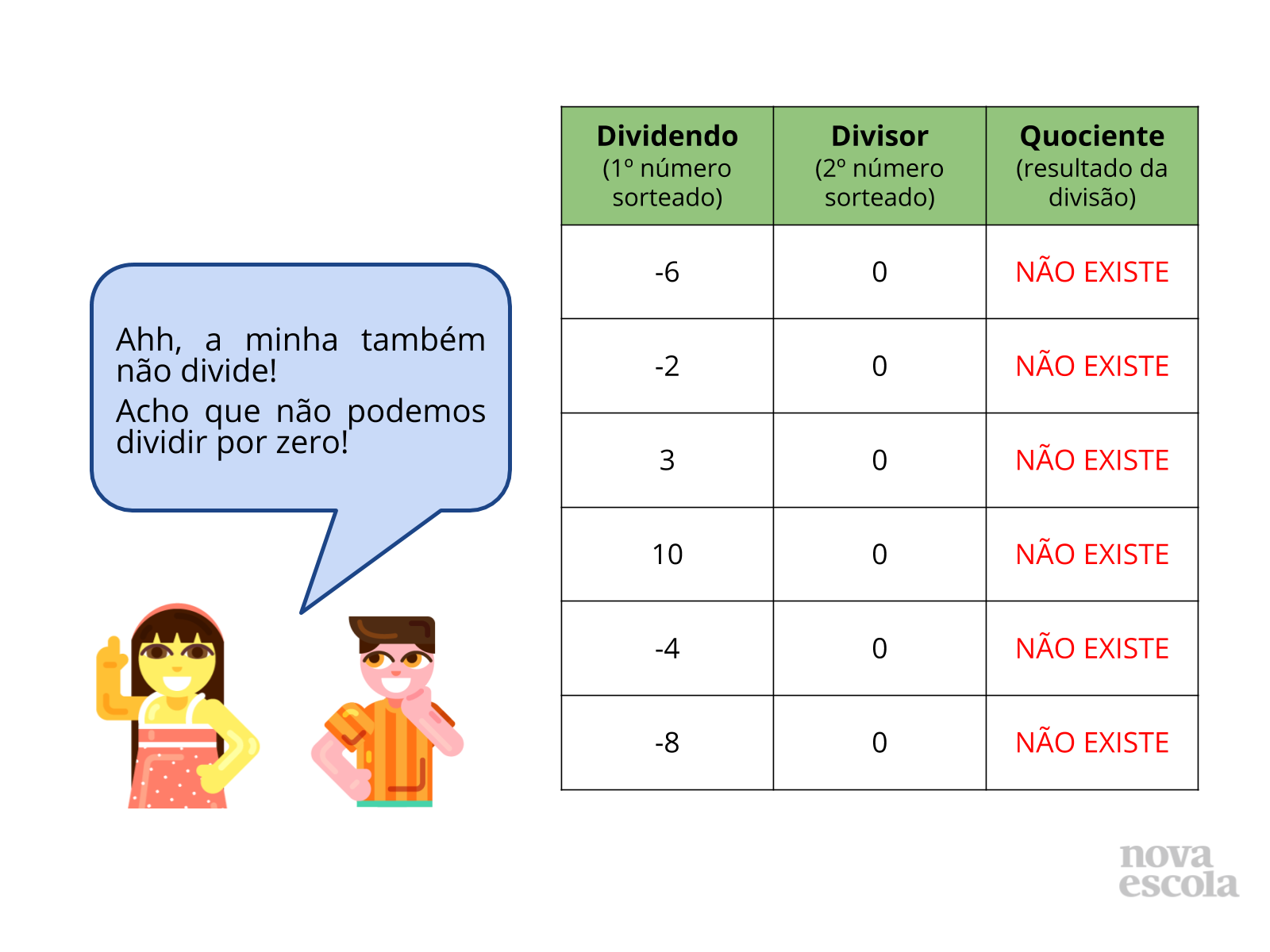
- O que aconteceu quando zero foi o segundo número sorteado? Qual foi o quociente da divisão?
- Qual fração pode representar o quociente 3? E o quociente -5?
Discussão da solução - parte II (slide 8)
Tempo sugerido: 7 minutos.
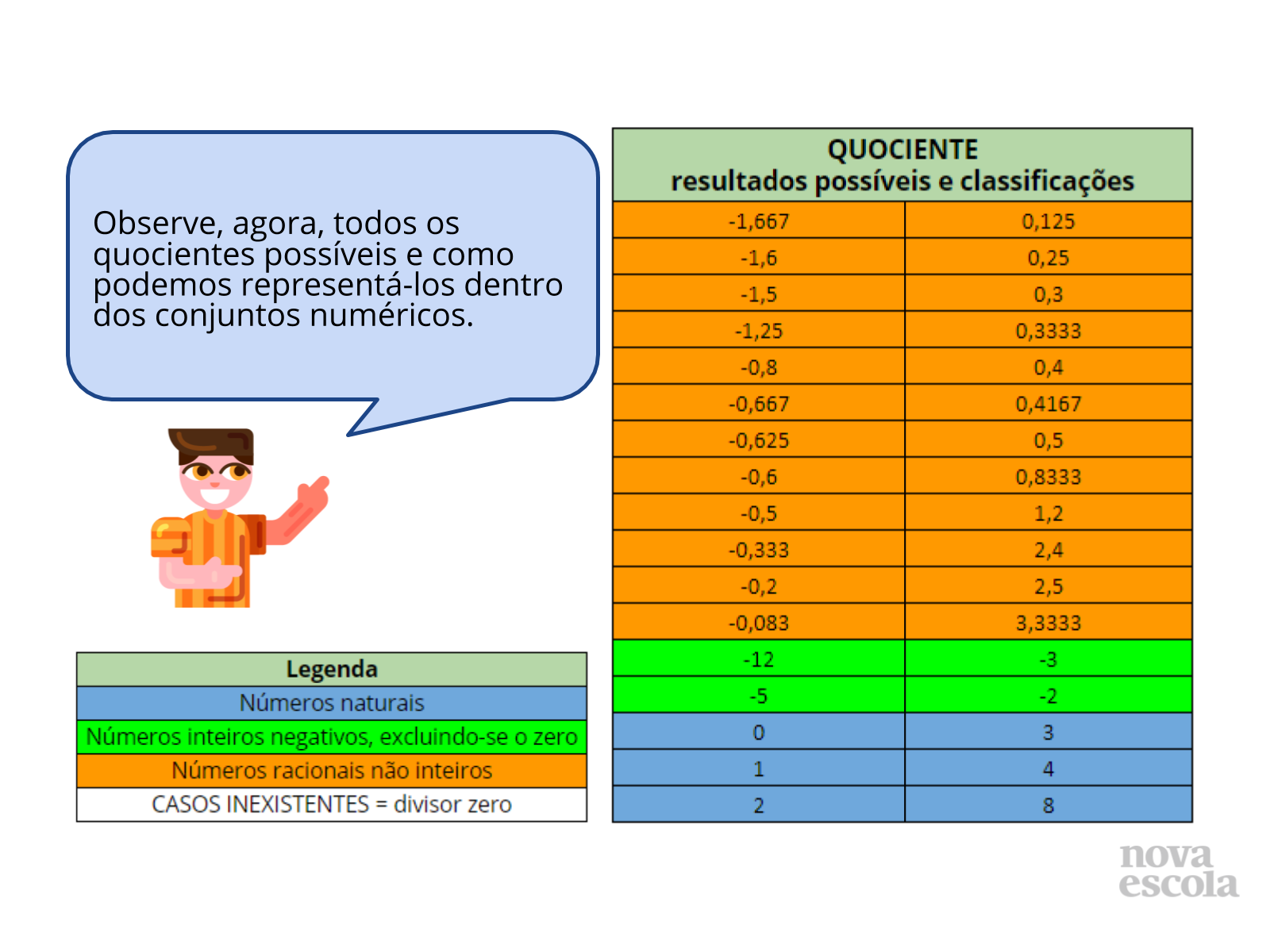
Orientação: Primeiramente, deixe os alunos compartilharem, para a sala, em quais conjuntos numéricos foram inseridos os quocientes encontrados. Depois, passe para esta série de slides, como forma de mostrar todos os resultados possíveis e a correta alocação dos mesmos nos conjuntos numéricos. Enquanto comentam sobre as alocações dos números, relembre que todos eles também podem ser representados em frações, logo, poderiam ser alocados em sua forma de fração. Caso não haja projetor, você pode apenas citar os quocientes possíveis e falar quais são as representações corretas dentro dos conjuntos numéricos no quadro da sala. É importante que, durante esse processo, sempre haja participação dos alunos nas respostas.
Propósito: Compartilhar as representações dos números nos conjuntos numéricos e ampliar o entendimento sobre número racional, de forma a conceituá-lo.
Discuta com a turma:
- Quais números vocês representaram como números naturais?
- Quais números vocês representaram como números inteiros negativos?
- Eu posso representar uma fração dentro dos números naturais? E dentro dos números inteiros?
- Os números naturais também são inteiros? São inteiros positivos ou negativos?
- Quais números vocês representaram como números racionais não inteiros?
- Existem números racionais inteiros? Dê um exemplo e explique o porquê.
Discussão da solução - parte 2 (slide 9)
Tempo sugerido: 4 minutos.
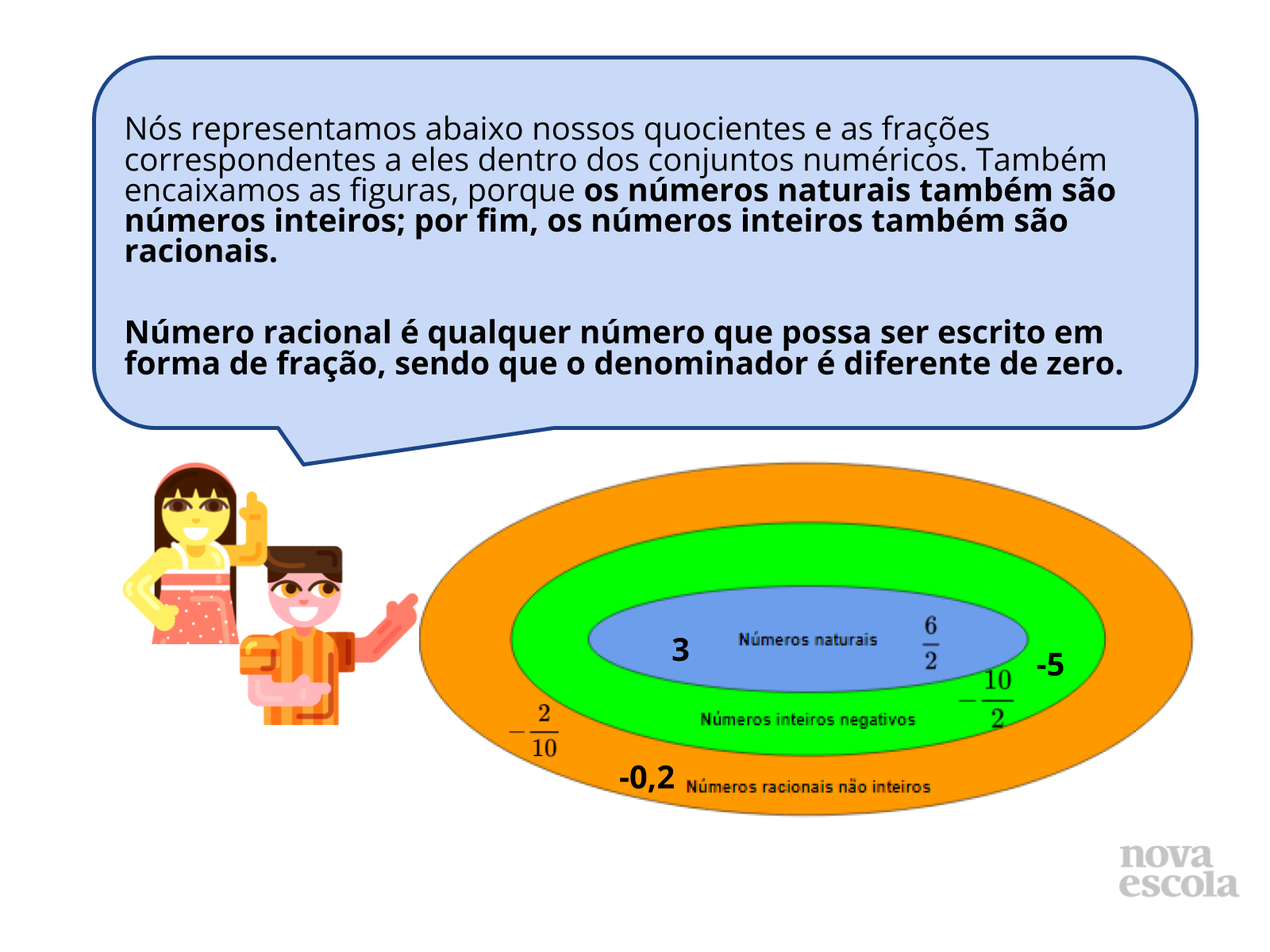
Orientação: Faça perguntas para que os alunos compreendam que os números inteiros são uma ampliação dos números naturais e, da mesma forma, os números racionais são ampliações dos números inteiros.
Propósito: Compartilhar as representações dos números nos conjuntos numéricos e ampliar o entendimento sobre número racional, de forma a conceituá-lo.
Discuta com a turma:
- Por que um número natural também é um número racional?
- Por que um número inteiro também é um número racional?
- O número 13/7 é racional? Por quê?
- E o número -86/13?
Sistematização do conceito

Tempo sugerido: 3 minutos.
Orientação: Apresente para os alunos a definição do conjunto dos Números Racionais, sempre fazendo uso da linguagem matemática e a tornando próxima dos alunos. Lembre-se de explicar a razão dos números racionais serem representados pela letra Q (devido ao fato de que representam quocientes). Depois, discuta com a turma alguns exemplos que se enquadram na definição.
Propósito: Definir conceitualmente o conjunto dos números racionais, com intuito de consolidar o aprendizado dos alunos.
Discuta com a turma:
- A partir dessas definições, quais exemplos de números que fazem parte do conjunto dos números racionais?
- Existe algum número natural que não é racional?
Encerramento
Tempo sugerido: 2 minutos.
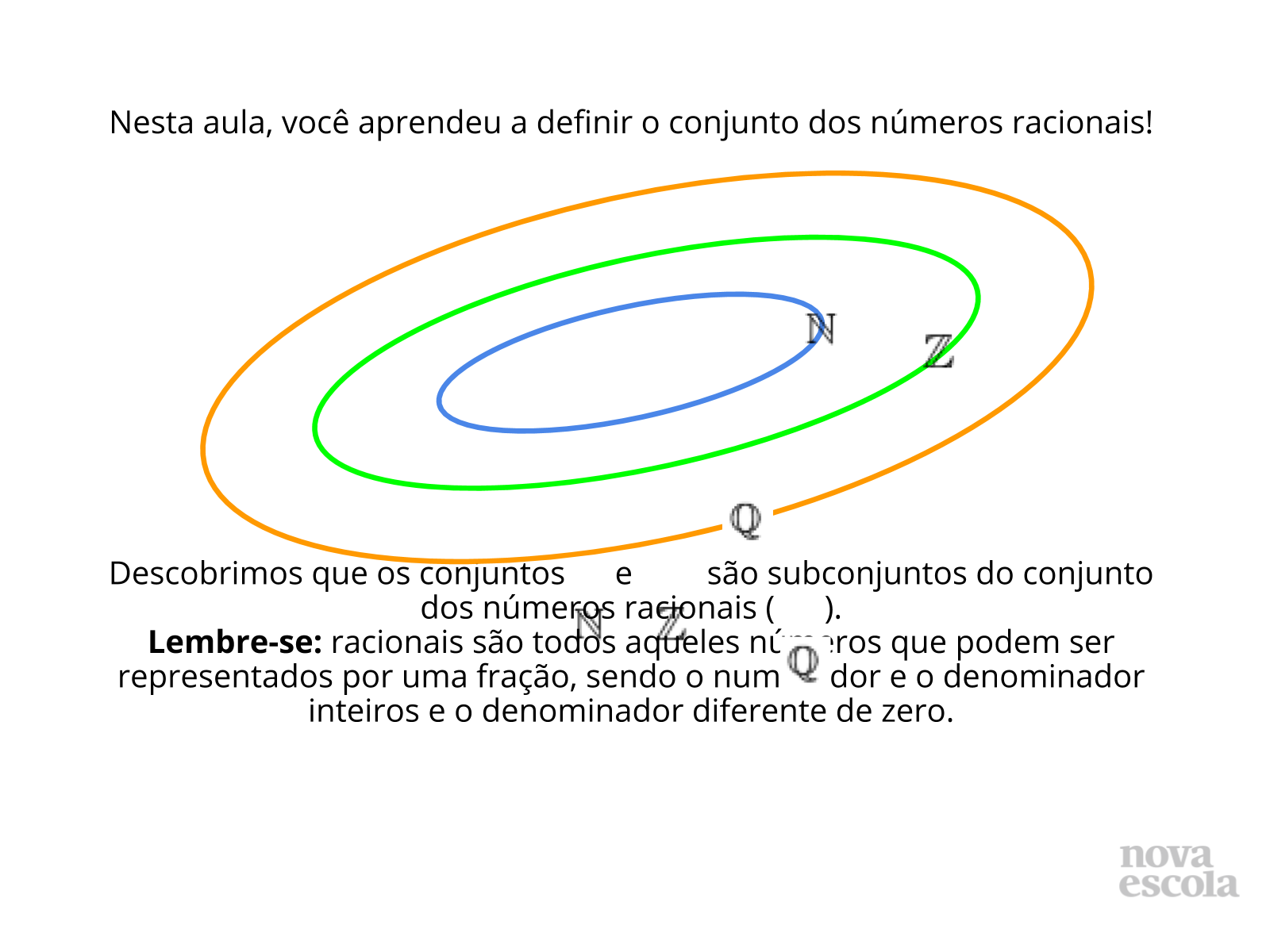
Orientação: Encerre a atividade retomando qual foi o aprendizado do dia. Vale ressaltar com os alunos que, entre dois números inteiros, há infinitos números racionais. Por fim, relembre o objetivo da aula e escolha 3 alunos que possam opinar sobre os seguintes tópicos:
- Você acha que atingimos o objetivo do dia?
- O que você aprendeu de novo hoje?
- O que você está ansioso para ver nas próximas aulas envolvendo números racionais?
Propósito: Resumir as aprendizagens da aula.
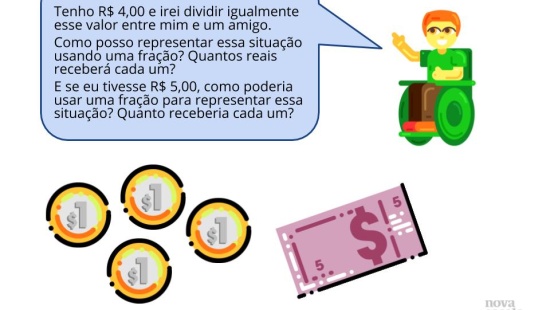
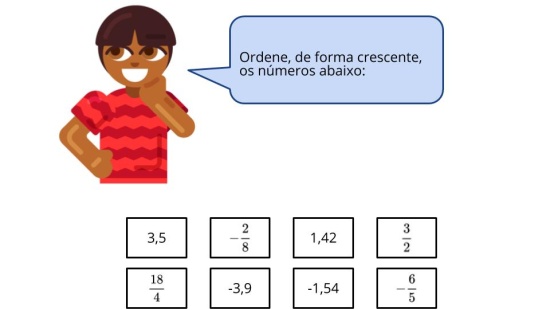
Raio X
Tempo sugerido: 7 minutos.
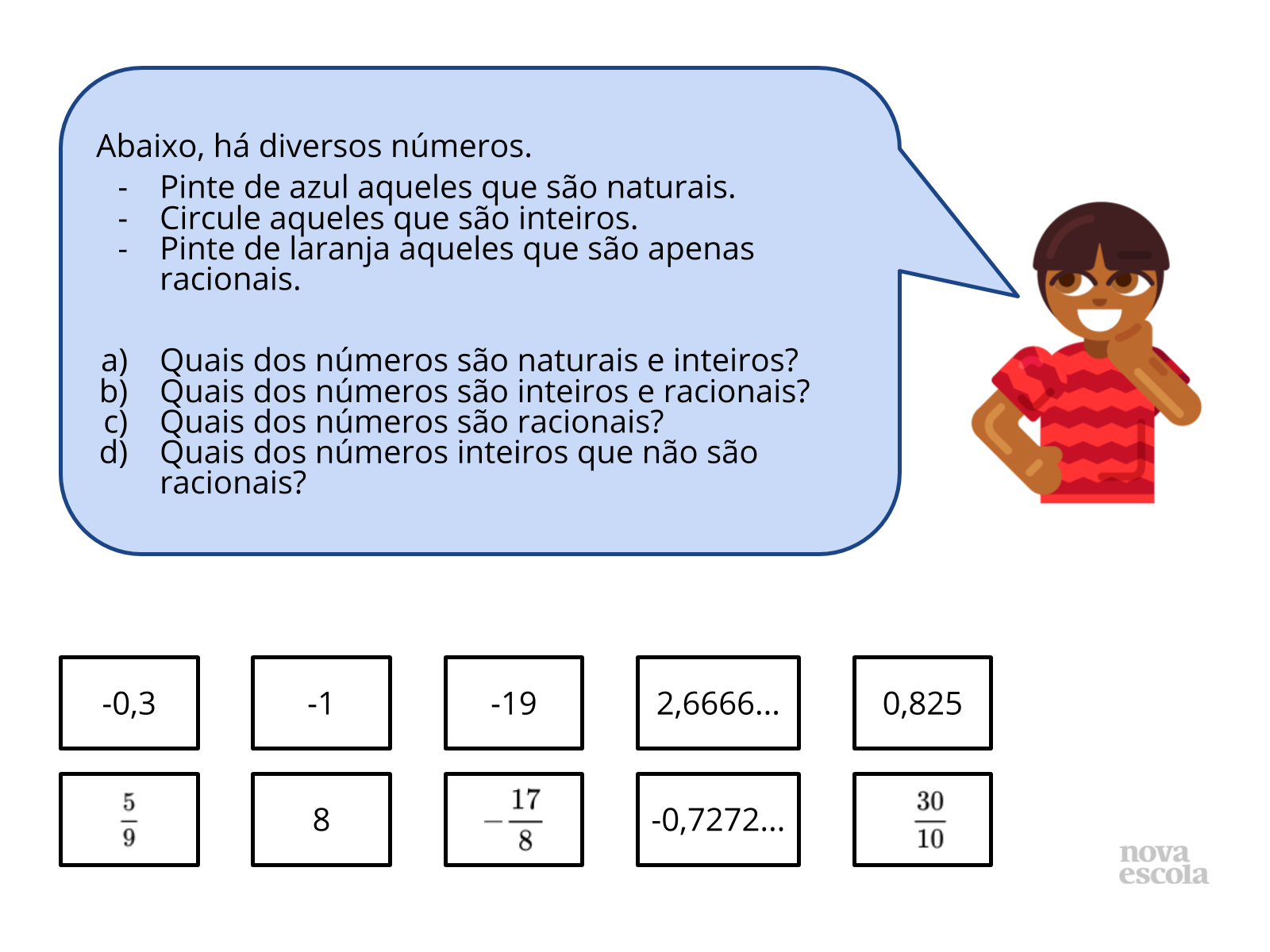
Orientações: Peça que, individualmente, os alunos leiam a atividade e anotem suas respostas no caderno. Circule para verificar se os alunos estão pintando e circulando corretamente, bem como respondendo às três perguntas. O Raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando algumas das respostas dadas pelos alunos.
Propósito: Verificar e avaliar se os alunos estão reconhecendo os números que compõem os conjuntos numéricos abordados em aulas.
Discuta com a turma:
- Existe algum número natural que não é inteiro ou racional?
- Existe algum número inteiro que não é racional?
- Todas as frações são números racionais?
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar