Objetivo
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Pedro Ramon Pinheiro de Souza
Mentor: Rodrigo Morozetti Blanco
Especialista: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF05MA09 - Resolver e elaborar problemas simples de contagem envolvendo o princípio multiplicativo, como a determinação do número de agrupamentos possíveis ao se combinar cada elemento de uma coleção com todos os elementos de outra coleção, por meio de diagramas de árvore ou por tabelas.
Objetivos específicos
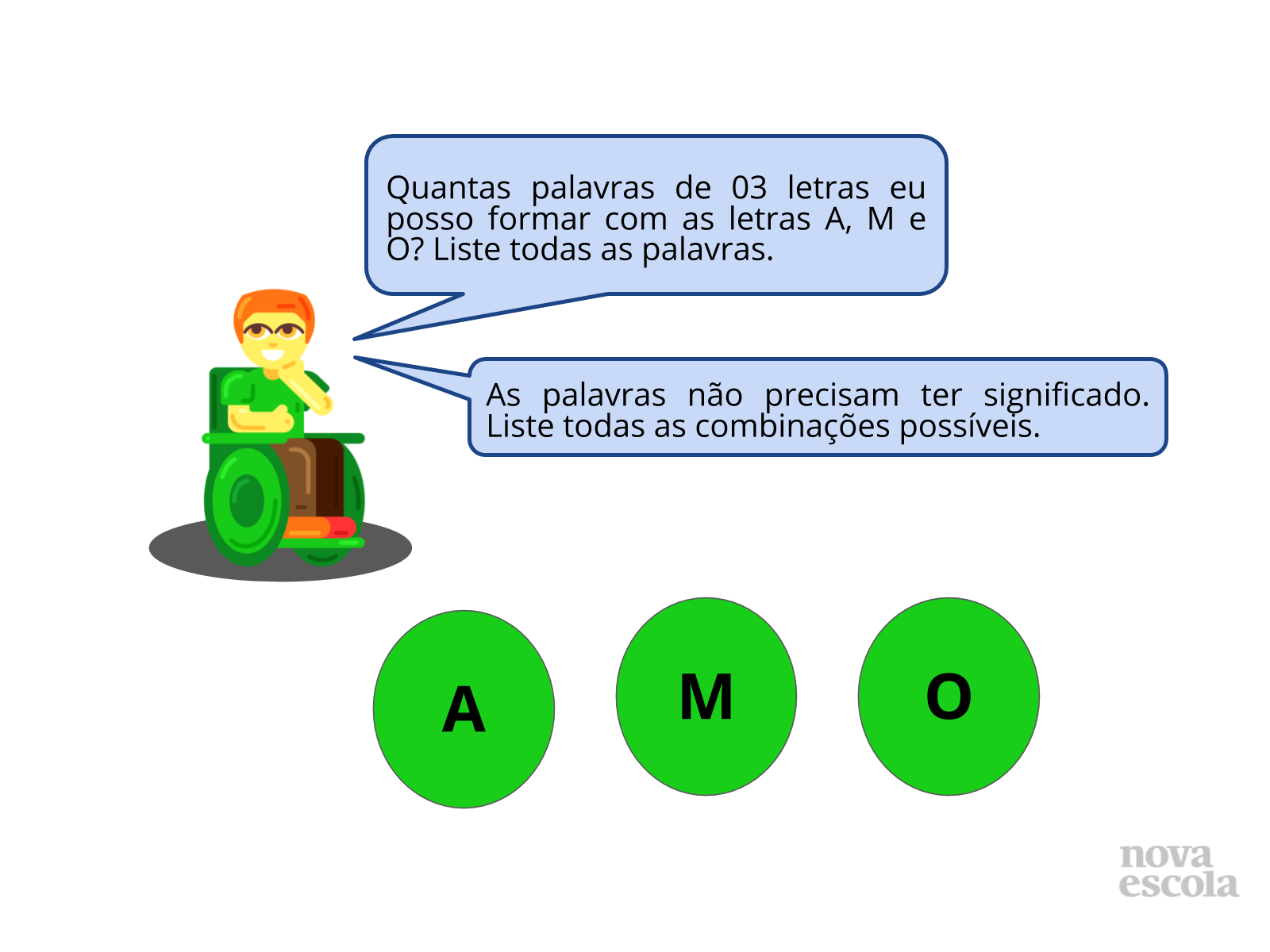
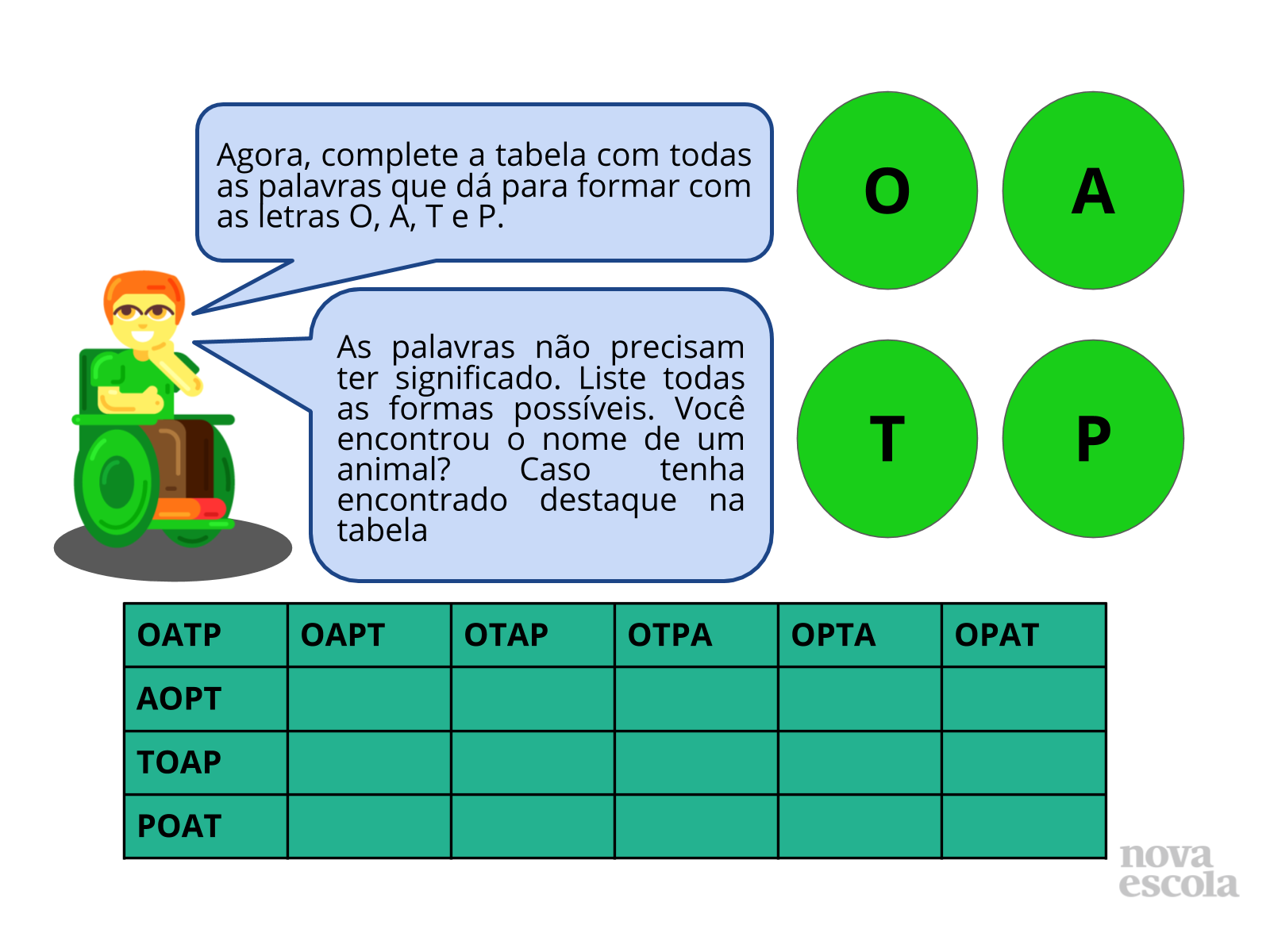
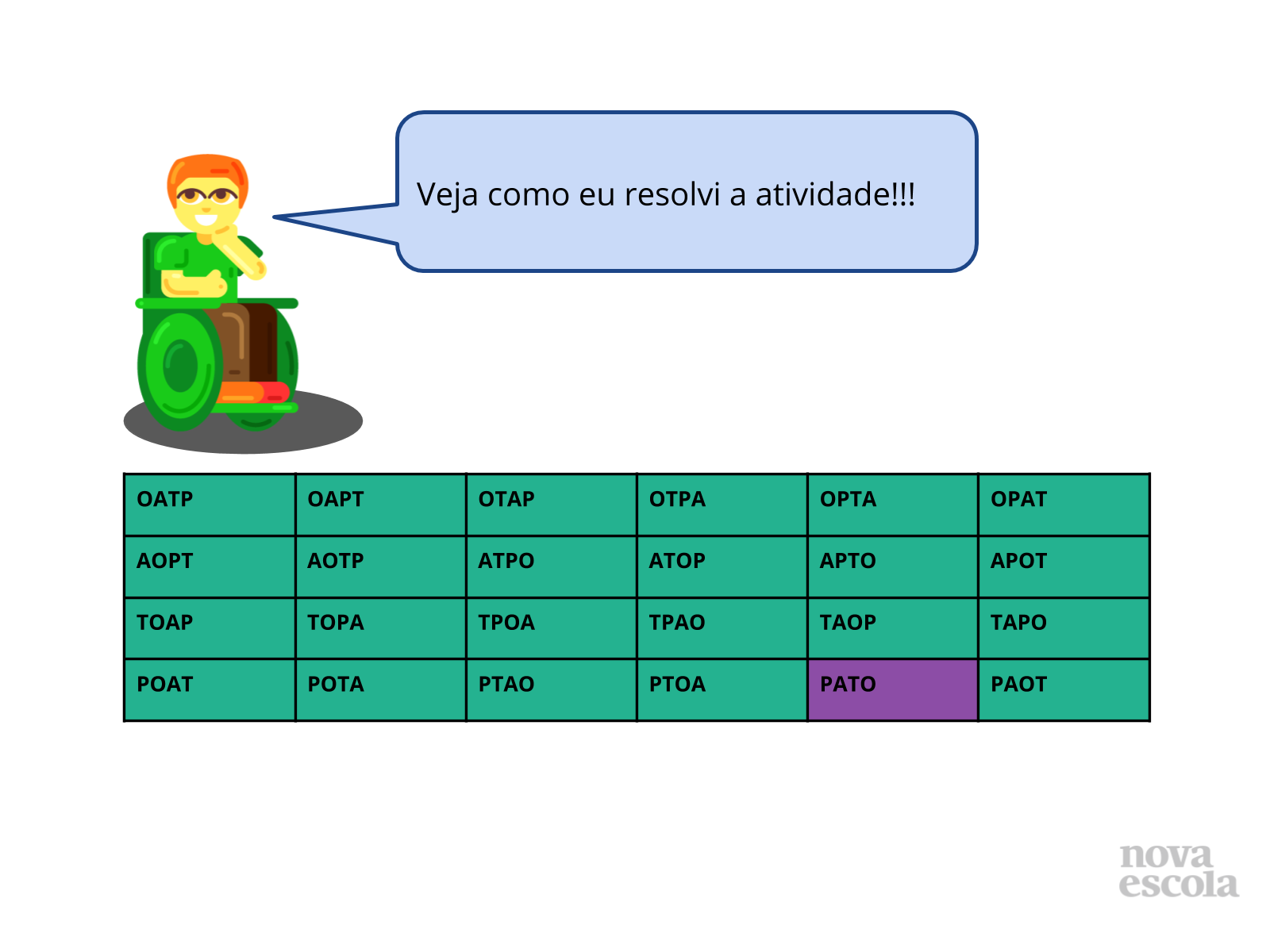
-Desenvolver estratégias para listar e ordenar todas as possibilidades de resposta de um problema de contagem
Conceito-chave
Contagem.
Recursos necessários
Lápis e papel.
Vocabulário que será adquirido nesta aula
Contagem, probabilidade.
Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
Tempo sugerido: 10 minutos.
Orientações: Você pode imprimir esta atividade ou escrever no quadro.
- Explique para a turma o conceito de anagrama;
- reforce para a turma o conceito de combinação;
- Veja se todos os alunos já entendem bem acerca deste tema;
- Veja se todos compreenderam bem o enunciado;
- Oriente que nesta atividade o objetivo é listar todas as possibilidades possíveis de combinação dessas 03 letras, ou seja, a combinação das letras não precisa ter significado;
- Dê atenção a todos os alunos para que nenhum fique de fora de processo de ensino-aprendizagem.
- Incentive a interação entre a turma, de maneira que, os alunos que têm mais facilidade em resolver o problema, ajudar aos que estão com dificuldade;
Propósito: Mostrar aos alunos que a partir da interação entre eles é possível dinamizar o processo de ensino-aprendizagem.
Discuta com a turma:
- Por onde devemos começar para resolver o problema?
- Que informações você precisa para resolver o problema?
- Qual é a melhor estratégia para listar todas as possibilidades sem repetir ou esquecer de nenhuma?
- É possível resolver este problema de uma outra forma?
- Materiais complementares:
Atividade principal
Tempo sugerido: 18 minutos.
Orientações:
- Você poderá escrever o texto do problema no quadro, projetá-lo ou entregar uma cópia aos alunos;
- Explique aos alunos que eles devem utilizar os conhecimentos e estratégias que já conhecem para solucionar o problema.
- Deixe que os estudantes leiam o problema e dê tempo para que tentem resolvê-lo;
- Não faça nenhuma intervenção neste momento, observe como os alunos analisam os dados do problema, interpretam e elaboram suas estratégias;
- Após o tempo necessário para a resolução do problema, peça que os alunos apresentem as suas soluções;
- Oriente aos alunos para preencher a tabela seguindo a ordem de combinações já fornecidas.
Propósito: Fazer com que os alunos mobilizem os conhecimentos que já possuem para resolver o problema e dinamizar a aula para uma melhor interação dos alunos.
Discuta com a turma:
- É possível resolver este problema de mais de um caminho?
- Qual a melhor maneira de resolver?
- Como você fez para listar todas as combinações?
- Qual estratégia você utilizou para não repetir nenhuma combinação?
- Materiais complementares:
Discussão da solução
Tempo sugerido: 06 minutos.
Orientação: Peça aos alunos para compartilharem suas estratégias e explicar como pensaram para resolver. Você pode escolher algumas duplas para apresentar suas soluções e estratégias usadas para montar preencher a tabela.
Discuta com a turma: Provoque os seguintes questionamentos para a turma.
- Pode me mostrar como você fez as combinações?
- Você acha que poderia fazer as combinações de outra forma?
- O que você acha sobre os modos de soluções de seus colegas?
- Qual a diferença entre o seu método de resolução e a dos seus colegas?
- Qual a semelhança entre as tabelas que vocês montaram?
Propósito: Promover interação entre os alunos e apresentar as estratégias adotadas para elaborar o problema e finalizar a árvore de possibilidades.
Encerramento
Tempo sugerido: 4 minutos.
Orientações: Encerre apresentando aos estudantes como, se feito da maneira correta, resolver problemas de contagem pode ser fácil.
Propósito: Sistematizar os conhecimentos adquiridos na aula.
Discuta com a turma:
- A maneira de fazer a contagem na hora de listar as possibilidades.
- Como identificar a melhor estratégia para resolver o problema em questão.
Raio x (Slides 7 e 8)
Tempo sugerido: 10 minutos.
Orientações: Apresente a nova situação e peça que os estudantes digam em voz alta alguns caminhos que podem seguir para resolvê-la. Você pode projetar, passar no quadro ou fazer cópia para os alunos. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um.
Propósito:
- Deixar que o processo de ensino aprendizagem ocorra através da maior interação que esta atividade propõe entre aluno e professor;
- Auxiliar os alunos a perceber que todas as estratégias de resolução de problemas são válidas e o mais importante é elaborar uma estratégia consistente e conseguir justificá-la matematicamente.
- Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da relação entre algumas porcentagens e suas frações equivalentes.
Discuta com a turma:
- Depois de tudo o que vimos nesta aula, qual a forma mais prática para resolver este problema?
- Existe outra forma de resolver este problema?
Materiais complementares:
Raio x (Slides 7 e 8)
Tempo sugerido: 10 minutos.
Orientações: Apresente a nova situação e peça que os estudantes digam em voz alta alguns caminhos que podem seguir para resolvê-la. Você pode projetar, passar no quadro ou fazer cópia para os alunos. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um.
Propósito:
- Deixar que o processo de ensino aprendizagem ocorra através da maior interação que esta atividade propõe entre aluno e professor;
- Auxiliar os alunos a perceber que todas as estratégias de resolução de problemas são válidas e o mais importante é elaborar uma estratégia consistente e conseguir justificá-la matematicamente.
- Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da relação entre algumas porcentagens e suas frações equivalentes.
Discuta com a turma:
- Depois de tudo o que vimos nesta aula, qual a forma mais prática para resolver este problema?
- Existe outra forma de resolver este problema?
